Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Geography, Physical
运动物体在特定时间访问不同类型兴趣点（POI）的可能性并不总是相同的，因此定量时间地理学研究需要考虑实际的POI语义信息，包括POI属性和时间信息。
- time geography
- space–time trajectory
- POI
- semantic information
- position probability
1. 引言
概率时间地理学认为，移动物体进入可到达位置点的可能性并不总是相同的[1]，并且与时空锚点之间的时空距离有关。地理第一定律指出，地理实体之间的空间距离越近，相关性越强。同样，在时间地理学中，时空锚点的时间成本越低，移动物体出现的可能性就越大。这意味着，在定量时间地理分析中，时空距离确定的时空锚点越近，运动物体出现的概率就越大。因此，研究人员期待在时间地理学中建立位置概率的定量测量模型。
Downs引入了一种考虑时空距离的位置概率测量模型，称为时间地理密度估计（TGDE）[2]。TGDE从历史经验数据的角度出发，通过计算两个相邻锚点与可到达点的时间距离来衡量待测点的访问概率。该方法将核密度估计与时间地理学相结合，遵循地理第一定律，构建了基于地理椭圆的时间地理密度估计模型。因此，任意两个相邻时空锚点之间移动物体的时空不确定性可以表示为概率密度云。这种概率密度云有两种使用方式：一是核密度估计[3]，即时空轨迹上所有密度云的叠加，用于表示运动物体在时空轨迹区域的原点距离估计;另一种是相互作用分析[4]，即同一时间段内密度云的交集分析，用于测量两个运动物体在时空轨迹周期内的相互作用概率。这种概率密度云建模方法在均匀空间中是有效的[5]。
然而，到目前为止，概率时间地理学的位置概率建模方法仍然停留在齐次空间中，只考虑了位置点的时间和空间信息，而忽略了语义属性信息。本文将进行两个重要的扩展。首先，将持仓概率的分布从反馈扩展到相互反馈;位置概率分配的经典方法是计算从时空锚点到被测点的时间代价，这是单向反馈，只考虑运动物体是否有足够的能力到达被测点的能力约束，是指运动物体的运动速度和时间的联合约束。但是，被测点的语义信息也会对移动物体的出入产生影响，例如在22：00后移动物体关闭超市或出入概率为0的情况下，属于能力约束。在考虑待测点的时间成本的基础上，考虑待测点的语义对访问概率的机理，形成锚点与待测点的“相互反馈模型”。然后，将同质空间的位置概率模型推广到异质空间，特别是城市空间。在城市空间中，活动场所常在地图上标注兴趣点（POI），因此POI可以用来表示运动物体所访问的时空位置点，在不同时期，不同类型的POI对运动物体具有不同的吸引力。包含语义属性信息的 POI 位置点可能会影响对移动对象的访问，例如在工作日，当孩子早上上学而不是去公园时。因此，我们将有一种计算异构空间中位置概率的方法。
2. 时间地理
时间地理学研究时空约束下运动物体的时空不确定性[9,10,11]。时空约束在时间地理学中可分为能力约束、权限约束和组合约束[8]。能力约束是指运动物体进行各种活动的能力受到限制，如运动物体具有自己的最大运动速度;权限约束是指移动物体在开展活动时受到法律、习俗和社会规范的限制，例如活动场所仅在营业时间开放时;组合约束是指在进行活动时，运动物体与其他运动物体或活动场所的相互作用，例如运动物体前往餐厅型POI位置点用餐[8]。时间地理学的研究分为定性研究和定量研究两大类。
在定性研究中，时间地理学主要采用三个关键概念：时空轨迹、时空棱镜和潜在路径区域（PPAs）来描述时空不确定性[12,13,14,15]。时空轨迹可以看作是地理位置点的时间序列，可以通过STP在时间地理上表示：
其中 STP 表示时空路径（图 1）;n 为轨迹点总数;l i 为运动物体的 ith 轨迹点，可描述为 （𝑥𝑖，，𝑦𝑖𝑡𝑖）、（𝑥𝑖，𝑦𝑖） 和 ti，，分别表示轨迹点的二维空间位置和时间戳。轨迹点有时称为锚点或控制点。STP表示运动物体的方向运动趋势，而时空棱镜可以表示运动不确定性的时空边界。时空棱镜表示在起点和终点、能力约束（如最大移动速度）和权限约束（如地理环境）的共同约束下，运动物体可以到达的所有可能的时空点的集合（图1a）。时空棱镜在平面空间中的足迹或投影称为PPA，在均匀空间中，它可以描述为以两个锚点（l i−1，li）为焦点的椭圆，并且vmax·(𝑡我−𝑡我−1)作为主轴：
其中 P P A i 表示第 i 个轨迹段上的 PPA，x 表示 PPAi 中的任意点， ||−||||−||表示二维空间中的欧几里得距离，t i−ti−1 是每对轨迹锚点的预算时间（𝑙𝑖−1，𝑙𝑖），vmax 是运动物体的最大移动速度。
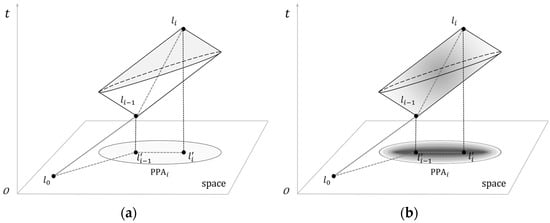
图 1.时间地理学的基本工具：（a）时空棱镜和PPA;（b）概率时空棱镜和概率PPA。
在定量研究中，时间地理学为 PPA 或时空棱镜中的每个位置点分配位置概率，以表示移动物体在给定时间访问某个可到达位置的可能性。因此，时间地理学的定量研究又称概率时间地理学，是时间地理学与概率论的融合[8]。其基本思想是，在PPA或时空棱镜中，在一对轨迹锚点出现时，运动物体在任何时候访问不同位置点的位置概率并不总是相等的，并且概率值的大小随着状态信息的变化而变化[16,17,18].对于任何可到达的位置点，通常根据从起点和终点到达该点的时间成本为位置点分配不同的位置概率，通常使用距离衰减核函数模型，如布朗桥和TGDE[7,16,19,20,21]。
时间地理学的定性和定量研究方法分析了运动物体的时空不确定性，并考虑了时间地理学的三个时空约束。这些方法在齐次空间中是有效的，特别是在不区分位置点的语义属性时，例如POI的类型和时间语义信息。然而，空间位置点的附着特性的差异会对运动物体产生不同的吸引力，并随时间而变化。
3. 兴趣点
POI是指地图上移动物体感兴趣的地理位置点，其信息包括位置、属性（类型）和时间[22\u23]。人们的旅行总是有一定的偏好和目的[24]，这就是为什么导航和计划在人们的旅程中是必不可少的。POI逐渐成为人们出行导航的关键搜索信息[25]，它与代表某些功能和需求的POI有关，因此成为人类活动分析的重要信息[26]。
不同类型的POI对个人的吸引力存在显着差异。例如，餐厅POI可能吸引人们就餐，旅游景点POI可能吸引人们进入，交通设施POI可能影响人们的生活习惯和出行选择，购物消费POI可能影响人们的消费行为，等等。POI位置的空间分布通常具有一定的聚集性[27]。例如，在城市商圈聚集了大量各种服务类型的POI，从而吸引附近的消费者出行。
相同类型的POI在不同时间段对个体的吸引力不同[28,29,30]。例如，餐厅POI在用餐时间对个人的吸引力远高于其他时间;在工作日，企业利益向标对个人的吸引力更大;旅游景点POI的吸引力在节假日普遍更大。POI能够较好地反映城市居民的时空活动行为，对运动物体进入时空位置点的行为具有较强的解释力。因此，在位置概率的定量计算中，有必要考虑实际的POI语义信息。
4. 时间地理学中的 POI
基于上述分析，可以得出结论，POI的吸引力对运动物体的进入有影响。对这种影响的定量描述将影响仓位概率的计算。单个运动物体的活动通常包括各种POI位置点，并且运动物体的时空轨迹与访问的POI位置之间存在时空接近。现有研究从两个方面分析了POI的吸引力。
曾先生提出了一种基于出租车轨道的城市POI吸引力变化分析方法[31]。他根据出租车在不同时间段停留在不同类别POI附近的距离，计算了不同时间段不同类别POI的吸引力和分布，然后统计分析了公民活动的规律。他认为，POI的吸引力与其属性、位置和时间段有关，现有方法忽略了时间和类别对POI吸引力的影响。该方法通过统计分析来评价POI的吸引力，呈现POI在大范围全局吸引力中的分布，但忽略了POI本身的语义信息以及POI对单一时空轨迹的个性化吸引力。此外，该方法需要大量独立的轨迹数据样本，在概率分布计算上缺乏先验性。Downs使用TGDE[2]为包括POI位置在内的空间位置分配访问概率，POI位置的访问概率反映了POI对移动物体的吸引力。该方法仅考虑时空轨迹的起点和终点，而不考虑POI位置相应活动的时间预算。该方法也忽略了POI的语义信息，缺乏基于经验数据的POI访问后验概率验证。
上述研究表明，POI语义信息对运动物体轨迹的影响存在显著差异，相应地，同一轨迹上的运动物体访问具有不同吸引力的POI的可能性也不同。在时间地理学中，一方面，POI的吸引力是时空位置点的不确定性度量，即通过大量时空轨迹进行时空位置统计的概率。另一方面，相对于时空轨迹，POI是运动物体在时空中可以到达的位置点，POI位置点处的访问活动也是时空轨迹锚点之间时间预算的一部分。
因此，基于时空轨迹预测时空不确定性的时间地理学需要将POI的语义信息纳入位置概率分布中，包括POI类型、时间因子等。目前，TGDE只考虑了空间位置和从位置点到两个锚点的时间成本，没有考虑POI在空间位置上的差异。该文基于已知的轨迹信息以及轨迹点与POI之间的时空距离，提出了一种考虑运动轨迹邻近性的POI概率模型。该模型基于移动速度和时间限制的时空约束，表达了已知精确时空位置点之间的时空不确定性，为这种时空不确定性测量提供了包括时间、空间和语义信息在内的所有信息，避免了单一信息带来的误差。该模型不仅为位置概率的量化提供了理论依据，而且为POI吸引力的统计提供了时间地理支持。例如，在运动物体的时空棱镜中，在计算通过POI的运动物体的时空轨迹时，可以排除不包含POI的轨迹。
This entry is adapted from the peer-reviewed paper 10.3390/ijgi13010022
This entry is offline, you can click here to edit this entry!
