Fluid-Structure Interaction Methods in Biomechanics

Fluid-Structure Interaction Methods in Biomechanics: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Mathematics, Applied

Contributor:

Fluid-structure interaction algorithms are utilized to examine how the human circulatory system functions by simulating blood flow and capturing mechanical responses within blood vessels. These sophisticated algorithms take into account interactions between fluid dynamics, vessel walls, heart walls, and valves. By combining advanced medical imaging techniques with fluid-structure interaction models, it becomes possible to customize these models for individual patients.

fluid-structure interaction
fluid
structure
interaction
blood
bioengineering
biomechanics

1. Introduction

The human circulatory system, also known as the cardiovascular system, is a complex network of blood vessels, organs, and tissues that transports oxygen, nutrients, hormones, and other essential substances throughout the body (Figure 1). It plays a crucial role in maintaining homeostasis and supporting the overall functioning of various organ systems. The circulatory system consists of several types of vessels that are responsible for different functions, as follows. (1) Arteries are blood vessels that carry oxygenated blood away from the heart and distribute it to various parts of the body. They have thick, elastic walls composed of smooth muscle and connective tissue, which allows them to withstand high blood pressure and pulsatile flow. Arteries progressively branch into smaller vessels called arterioles. (2) Arterioles are smaller branches of arteries that further divide into capillaries. They regulate blood flow and control blood pressure by constricting or dilating their smooth muscle walls. The diameter of arterioles can be adjusted to redirect blood flow to specific tissues or organs as needed. (3) Capillaries are the smallest and thinnest blood vessels in the circulatory system. They connect arterioles and venules and form an extensive network throughout the body’s tissues. Capillaries are responsible for the exchange of oxygen, nutrients, waste products, and hormones between the blood and surrounding tissues. The thin walls of capillaries allow for efficient diffusion of substances. (4) Venules are small vessels that receive deoxygenated blood from capillaries and merge to form veins. They collect blood from capillary beds and transport it to larger veins. Venules also play a role in the immune response by allowing white blood cells to migrate from the bloodstream to infected or injured tissues. (5) Veins are blood vessels that carry deoxygenated blood from various tissues and organs back to the heart. Unlike arteries, veins have thinner walls and lower blood pressure. They have valves that prevent the backflow of blood and aid in propelling blood toward the heart. Veins progressively merge to form larger vessels, returning blood to the heart through the superior and inferior venae cavae, and entering the right atrium. (6) The heart is a muscular organ located in the chest cavity and serves as the central pump of the circulatory system. It consists of four chambers: two atria (left and right) and two ventricles (left and right). The heart’s contraction (systole) and relaxation (diastole) generate the pumping action that propels blood throughout the circulatory system. The left side of the heart receives oxygenated blood from the lungs and pumps it into systemic circulation, while the right side receives deoxygenated blood from the body and pumps it to the lungs for oxygenation. (7) Pulmonary circulation refers to the pathway of blood from the heart to the lungs and back. Deoxygenated blood from the body enters the right atrium, passes through the right ventricle, and is pumped to the lungs via the pulmonary arteries. In the lungs, carbon dioxide is exchanged for oxygen, resulting in oxygenated blood. Oxygenated blood then returns to the heart through the pulmonary veins, entering the left atrium. (8) Systemic circulation is the pathway of blood from the heart to the body’s tissues and back. Oxygenated blood from the left atrium enters the left ventricle and is pumped out to the entire body through the aorta, the largest artery. Branches of the aorta distribute blood to various organs, and oxygen and nutrients are exchanged in the cap.

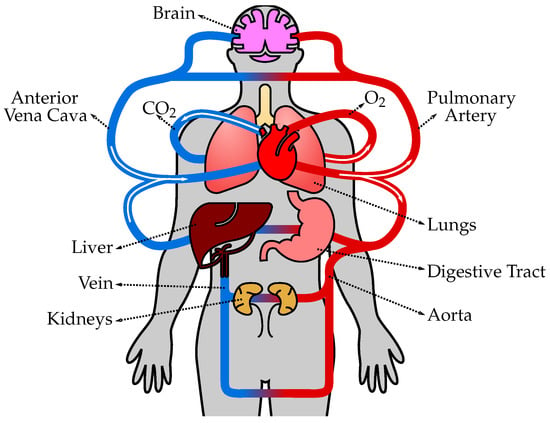
Figure 1. The human circulatory system consists of the heart, blood vessels, and blood, working together to transport oxygen, nutrients, hormones, and waste products throughout the body. The heart pumps oxygenated blood from the lungs to the body tissues through arteries, and deoxygenated blood is then returned to the heart through veins to be pumped to the lungs for oxygenation again.

The prospective utilization of computational models to augment our comprehension regarding the circulatory system and hemodynamics is significant. Advanced imaging techniques such as computed tomography (CT) and magnetic resonance imaging (MRI) can be leveraged for the creation of three-dimensional models of blood vessels. Computational fluid dynamics, also known as CFD, constitutes one tool that facilitates analyzing the bloodstream through a vessel with tri-dimensional innovation geometry along with inlet–outlet velocity profiles that are extracted from non-invasive sources, like MRI scans detecting fluid movement [1]. The CFD has both strengths and weaknesses when it comes to modeling the circulatory system and hemodynamics. One of its major strengths is the ability to utilize noninvasive imaging techniques like MRI to track fluid movement [2]. However, there are also limitations associated with this approach, such as restrictions in resolution that may affect the accuracy of the results. Additionally, wall movements are not taken into consideration which can impact the overall accuracy of predictions made by these models. To overcome some of these limitations, fluid-structure interaction (FSI) algorithms prove advantageous as they allow for modeling deformable structures and interactions between fluids within those structures [3]. These algorithms enable a more comprehensive understanding of how fluid interacts with dynamic systems.

Nonetheless, the effectiveness of CFD is impeded by restricted resolution capabilities and an inability to consider wall movements associated with elastic artery walls during the computation of blood flow through these vessels, leading researchers to explore alternative approaches, such as the employment of FSI techniques. These methods effectively account for deformable structures and their interactions with the fluids, thereby surpassing the effectiveness and practicality achieved by conventional CFD. Furthermore, FSI methods enable a more realistic simulation of flow patterns and provide improved insight into how blood flow phenomena in vessels are affected overall [4,5].

1.1. FSI Modeling Techniques

FSI modeling involves the simultaneous solution of fluid dynamics equations and structural mechanics equations to accurately capture the interaction between blood flow and the compliant vessel walls. Numerical methods, such as the finite element method (FEM) and finite volume method (FVM), are commonly employed to solve the coupled equations [6,7]. These techniques allow for the realistic simulation of phenomena such as wall deformation, fluid-structure interactions, and flow-induced forces, providing a comprehensive understanding of the hemodynamics within the circulatory system.

The immersed boundary method (IBM) is a technique for incorporating boundary conditions and collaborating with different solvers. It can be utilized in conjunction with both FEM and FVM, as well as other methods. The fluid component can be computed using the lattice Boltzmann methods, which have been proven to be highly effective compared to alternative approaches. The IBM has already been successfully employed in simulations of blood flow, exhibiting faster execution times than traditional CFD methods [8].

Alternatively, mesh-free approaches, also known as meshless methods, may be employed. These computational techniques do not require conventional structured or unstructured grids for discretizing the computing domain. Instead of using these traditional structures, distributed data points or particles are utilized to represent geometry and solve governing equations in a diverse manner. For blood vessel interactions applicable to FSI simulations, utilizing meshless methodologies can offer several advantages over other alternatives.

Key factors considered in FSI methods encompass wall shear stress, strain, stress, elastic modulus (E), and pulse wave velocity (PWV). Elevated levels of stress and strain on a blood vessel can increase the risk of complications such as rupture [9]. By utilizing FSI techniques to evaluate these parameters, it is possible to detect and manage potential issues at an early stage. Additionally, heightened aortic pulse wave velocity, which serves as a marker for arterial stiffness, has been associated with increased mortality rates in clinical populations [10]. Furthermore, employing FSI to measure the PWV of vessels enables us to assess their stiffness level and predict the likelihood of complications occurring [11].

1.2. Applications in Cardiovascular Research

FSI computational algorithms have been extensively utilized in cardiovascular research to investigate a wide range of physiological and pathological conditions. These include the assessment of hemodynamic parameters, such as wall shear stress, pressure distribution, and flow patterns, which are crucial for understanding disease progression and identifying regions of high stress and vulnerability. FSI models have been employed to study phenomena such as arterial stenosis, aneurysm formation and ruptures, atherosclerosis, and the performance of cardiovascular devices, such as stents and heart valves. The ability to simulate patient-specific geometries and conditions has opened up avenues for personalized medicine, allowing clinicians to tailor treatment strategies based on individual patient characteristics [12].

2. Fluid-Structure Interaction Techniques

The FSI simulations involve solving a set of coupled partial differential equations that describe the fluid flow equations (e.g., Navier–Stokes equations) and the structural mechanics equations (e.g., the elasticity equations) [15]. These equations are solved iteratively to account for the mutual interaction between fluid and structure at each time step. The computational framework incorporates advanced numerical methods and algorithms to accurately capture the dynamic behavior of both fluid and structure [16]. In computational simulations involving FSI, several algorithms are employed to effectively model and capture the dynamic interaction between fluid flow and structural behavior, as follows.

–: Monolithic approach: In the monolithic approach, the governing equations for fluid flow and structural mechanics are solved simultaneously within a single computational framework [17]. This approach involves coupling the fluid and structural equations and solving them together, often using an iterative procedure. It provides accurate and robust predictions of the fluid-structure interaction but can be computationally demanding.
–: Partitioned approach: The partitioned approach separates the fluid and structural equations into two independent solvers, which are then coupled through an interface. Each solver operates independently, and the information is exchanged at the interface during the simulation. This approach allows for the use of existing specialized solvers for fluid and structural problems, making it computationally efficient [18].

The partitioned approach is further distinguished into two distinct strategies using computational techniques known as one-way and two-way methods. These approaches vary in their methodology towards simulating the interplay between fluid flow and solid structures.

–: One-way FSI: In one-way FSI, also known as loosely coupled FSI, the fluid and structural domains are treated as separate and independent simulations. The fluid flow is first simulated using CFD techniques, and the resulting fluid forces are applied as boundary conditions to the structural analysis. The structural deformation, in turn, influences the fluid flow indirectly through these imposed boundary conditions. The information exchange between the fluid and structural domains is performed in a one-way manner, with the fluid providing the driving forces for the structural response. This approach is computationally efficient but assumes that the structural deformation has a negligible impact on the fluid flow [19].
–: Two-way FSI: On the other hand, two-way FSI, also known as fully coupled FSI, considers the fluid and structure as a coupled system that interact with each other. In this approach, the fluid and structural equations are simultaneously solved in a fully coupled manner, accounting for the mutual influence between the two domains. The fluid forces affect the structural deformation, and the resulting deformation alters the fluid flow patterns. The information exchange occurs bidirectionally, allowing for a more accurate representation of the fluid-structure interaction. Two-way FSI is more computationally demanding but provides a more realistic representation of the physical phenomena involved [20].

The main difference between one-way and two-way FSI lies in the level of coupling and information exchange between the fluid and structural domains. One-way FSI assumes a one-sided influence of the fluid on the structure, while two-way FSI considers a fully coupled interaction where both the fluid and structure mutually affect each other. It is worth noting that the FSI algorithm choice depends on various factors, including the complexity of the problem, computational resources, desired accuracy, and the specific objectives of the simulation. Researchers and engineers select the most appropriate algorithm based on these considerations to ensure accurate and efficient simulations of fluid-structure interactions. The following are some commonly used FSI algorithms.

In the subsections below, the partitioned FSI approach is described using different methods. The coupling between the two solvers is achieved by explicitly defining boundary conditions at the fluid-structure interface, either through explicit iterations or other suitable strategies. A partitioned FSI approach is one of several methodologies used in FSI simulations. In contrast to the partitioned approach, some FSI techniques involve solving a monolithic system of equations, where the coupled equations for fluid and structure are solved simultaneously. In this monolithic approach, the fluid and structure equations are combined into a single set of equations, and a unified solver is used to solve them. The choice between the partitioned and monolithic approaches depends on various factors, such as the complexity of the problem, computational efficiency, and desired accuracy. However, the numerical methods presented herein specifically pertain to different approaches for solving the fluid dynamics component within the partitioned FSI framework. These methods offer researchers a range of options to tackle the fluid dynamics problem while adhering to the principles of partitioned coupling. By exploring and comparing these diverse numerical methods, researchers can gain insights into the strengths and limitations of each approach within the context of their FSI simulations.

2.1. Arbitrary Lagrangian–Eulerian Method

The interaction between fluid and its surrounding structures is an ever-present aspect of biology that plays an integral role in the vasculature of the human body [21]. Such interactions can be modeled through algorithms such as arbitrary Lagrangian–Eulerian (ALE) methods [22], which create a body-fitted resolution of the flow and stress distribution between fluid and its surrounding structure. The ALE methods are dependent upon the use of meshes with high density. As such, users tend to use simplified geometries to decrease the elements for stable calculations. They might, thus, be ill-suited to represent complex patient-specific geometries due to issues with modeling gaps between solid and fluid domains [23].

The ALE method combines the advantages of Lagrangian and Eulerian formulations by tracking the motion of the fluid mesh. It enables the mesh to move with the fluid, accommodating structural deformations, while also providing a fixed Eulerian framework for solving the fluid equations. This method is widely used in simulating FSI problems with large deformations. The ALE method can be implemented within both partitioned and monolithic approaches in FSI simulations, depending on the specific implementation and computational framework used.

–: Partitioned approach: In the partitioned approach, the ALE method separates the fluid and structural equations into independent solvers. The fluid equations are solved using an Eulerian formulation, where the fluid mesh moves with the fluid motion. The structural equations are typically solved using a Lagrangian formulation, where the structural mesh remains fixed. The information is exchanged between the fluid and structural solvers at the fluid-structure interface, allowing for the interaction between the fluid and structure.
–: Monolithic approach: In the monolithic approach, the ALE method involves solving the fluid and structural equations simultaneously within a single computational framework. The fluid and structural equations are coupled and solved together in a fully coupled manner. This approach provides a more tightly coupled representation of the fluid-structure interaction, where the motion of the fluid mesh and the structural deformation are considered concurrently.

Both approaches have their advantages and drawbacks. The partitioned approach allows for flexibility in choosing specialized solvers for fluid and structural problems, which can be computationally efficient. On the other hand, the monolithic approach provides a more integrated and accurate representation of the fluid-structure interaction but can be more computationally demanding. The choice between the partitioned and monolithic approaches depends on various factors, including the complexity of the problem, computational resources, desired accuracy, and the specific objectives of the simulation. Researchers and engineers select the most suitable approach based on these considerations to effectively capture the FSI using the ALE method.

2.2. Immersed Boundary Method

An alternative to body-fitted models is the immersed boundary formulation [24]. First introduced by Peskin in 1972, such methods use overlapping components of fluid and structure, avoiding many complications of mesh regeneration encountered in ALE methods [25]. One of the major advantages of the immersed method is that the equations are represented on a Cartesian grid, allowing for moving boundaries and simpler grid generation [23]. Thus, the IBM is commonly used when the fluid flow interacts with complex or deformable boundaries [26]. It represents the boundaries as an additional force term in the fluid equations, allowing for efficient simulations without explicitly modeling the boundary geometry. This method is particularly useful in simulating fluid-structure interactions with flexible structures, such as heart valves or blood vessel walls. The IBM method is typically implemented within the context of a partitioned approach in FSI simulations. In the partitioned approach, the fluid and structural equations are solved separately using independent solvers, and the information is exchanged at the fluid-structure interface. The fluid equations are solved using a traditional fluid solver, such as a finite volume or finite element method, while the structural equations are solved using a separate structural solver. The IBM represents the presence of the solid structure as an additional force term in the fluid equations, allowing for the interaction between the fluid and the deformable solid boundaries. The partitioned approach is well-suited for incorporating IBM because it allows for the decoupling of the fluid and structural solvers. The fluid solver does not need to explicitly know the details of the immersed boundaries, as the forces are incorporated as source terms in the fluid equations. This approach provides computational efficiency by leveraging existing specialized solvers for fluid and structural problems.

2.3. Embedded or Embedded-Boundary Method

The embedded or embedded-boundary method involves representing the solid structure as a mesh embedded within the fluid mesh. This method allows for efficient simulations by using the fluid mesh to solve the fluid equations and incorporating the solid boundary conditions within the embedded structure [27]. It is particularly useful when dealing with complex geometries or when the fluid-structure interface changes during the simulation. The embedded or embedded-boundary method can be implemented within the context of either a partitioned or monolithic algorithm in FSI simulations, depending on the specific implementation and computational framework used.

–: Partitioned approach: In the partitioned approach, the embedded or embedded-boundary method involves separating the fluid and structural equations into independent solvers. The fluid equations are typically solved using a traditional fluid solver, such as a finite volume or finite element method, where the fluid mesh remains fixed. The structural equations are solved separately using a structural solver. The information is exchanged at the fluid-structure interface to account for the interaction between fluid and structure.
–: Monolithic approach: In the monolithic approach, the embedded or embedded-boundary method solves the fluid and structural equations simultaneously within a single computational framework. The fluid and structural equations are coupled and solved together in a fully coupled manner. This approach provides a more tightly coupled representation of the fluid-structure interaction, where the fluid mesh and structural deformations are considered concurrently.

Both approaches have their advantages and limitations. The partitioned approach allows for flexibility in using specialized solvers for fluid and structural problems, which can be computationally efficient. The monolithic approach provides a more integrated and accurate representation of the fluid-structure interaction but may be more computationally demanding. The choice between the partitioned and monolithic approach for the embedded or embedded-boundary method depends on various factors, such as the specific problem, computational resources, desired accuracy, and the objectives of the simulation. Researchers and engineers select the most appropriate approach based on these considerations to effectively model and simulate the fluid-structure interaction using the embedded or embedded-boundary method. These algorithms can be further complemented with advanced numerical techniques, such as finite element methods, finite volume methods, or meshless methods, depending on the specific requirements and characteristics of the FSI problem.

2.4. Meshless Methods

Meshless methods, also known as mesh-free methods, are numerical techniques that do not rely on traditional structured or unstructured meshes for discretizing the computational domain [28]. Instead, these methods use a set of scattered data points or particles to represent the geometry and solve the governing equations. In the context of FSI simulations for blood vessel interactions, meshless methods offer several advantages.

One popular meshless method used in FSI simulations is the smoothed particle hydrodynamics (SPH) method. SPH represents the fluid and structure as a set of particles, where each particle carries properties such as position, velocity, and other relevant physical quantities. In SPH, the computational domain is discretized by placing particles throughout the domain, including the fluid and structural regions. For fluid simulation, SPH applies a smoothing kernel to evaluate the interactions between neighboring particles, allowing for the computation of fluid properties like pressure and velocity. The fluid equations, such as the Navier–Stokes equations, are solved by evaluating the interactions among the particles using this kernel function. The fluid particles interact with each other and with the solid particles representing the blood vessel walls, enabling the simulation of fluid-structure interactions.

In the case of blood vessel interaction, the deformations and motions of the vessel walls are typically governed by structural equations, such as the equations of linear elasticity. The solid particles representing the vessel walls are subject to external forces from the surrounding fluid particles, allowing for the simulation of the interaction between the fluid and the deformable vessel walls. Meshless methods in FSI simulations for blood vessel interaction offer several advantages. They can handle large deformations and complex geometries without the need for re-meshing or re-gridding. They are well-suited for modeling free surface flows and multiphase flows, where the fluid domain and interfaces can evolve dynamically. Meshless methods also provide flexibility in capturing fluid-structure interfaces and handling fluid-structure coupling. Ongoing research and advancements in meshless methods continue to improve their efficiency and accuracy in modeling FSI with complex geometries [29].

Similarly, meshless methods can be implemented using both partitioned and monolithic approaches in FSI simulations, depending on the specific implementation and computational framework used.

–: Partitioned approach: In the partitioned approach, the meshless method separates the fluid and structural equations into independent solvers. The fluid equations are typically solved using the meshless method, where the computational domain is discretized by a set of particles or scattered data points. The structural equations are solved separately using another meshless method or a different numerical technique suitable for structural analysis. The information is exchanged at the fluid-structure interface to account for the interaction between fluid and structure.
–: Monolithic approach: In the monolithic approach, the meshless method involves solving the fluid and structural equations simultaneously within a single computational framework. The fluid and structural equations are coupled and solved together in a fully coupled manner. This approach provides a more tightly coupled representation of the fluid-structure interaction, where the fluid particles and the structural particles or nodes interact directly and are solved concurrently.

The SPH technique has the inherent characteristic of preserving mass balance, and its ability to trace a surface automatically eliminates the need for repeated regeneration of mesh in response to deformations [30,31]. SPH discretizes a continuum into a set of particles, which interact through a kernel interpolation function with a radius known as the smoothing length. A particle’s physical properties are obtained by summing the properties of all of the particles within the kernel. The accuracy of SPH relies upon characteristics such as smoothing length, flow viscosity, and particle size amongst others [32,33]. The recent development of multi-resolution SPH further increases the resolution of fluid flow by splitting particles into regions of interest and merging particles where lower resolution is adequate [34,35]. One of the advantages of SPH is in modeling damage to blood vessels. Whereas mesh-based models are not well suited to model damage to an artery due to such damage continually decreasing stored energy, SPH can model such processes using particle-based methods to model the flow of blood. Each particle contains mechanical information such as stress, strain, position, and velocity. This allows for input equations to model stress on the surrounding structures and calculate the damage to the particles [36,37,38]. Due to these capabilities of modeling nonlinear large deformations, SPH has been used not just for the hemodynamics of arteries, but also for the more complex modeling of blood flow through the heart and its valves [39].

The choice between the partitioned and monolithic approaches for meshless methods in FSI simulations depends on various factors, including the complexity of the problem, computational resources, desired accuracy, and the specific objectives of the simulation. Researchers and engineers select the most suitable approach based on these considerations to effectively capture the FSI using meshless methods. Figure 2 showcases the flowcharts demonstrating solution algorithms for FSI, incorporating both ALE and SPH methods.

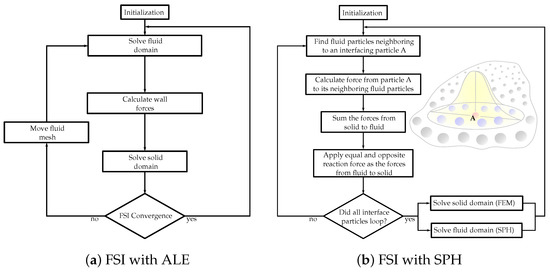
Figure 2. Flowcharts of the FSI solution algorithms with (a) Arbitrary Lagrangian–Eulerian (ALE) and (b) smoothed-particle hydrodynamics (SPH) methods.

2.5. Added Mass Effect

In FSI algorithms, the “added mass effect” refers to the phenomenon where the surrounding fluid exerts an inertial force on a structure undergoing motion, or, in other words, the surrounding fluid moves with the same velocity as that of the immersed boundary [40]. This effect occurs because the structure displaces fluid as it moves, resulting in an increase in mass that must be accelerated or decelerated along with the structure. In academic literature, the term “added mass effect” denotes numerical instabilities that often arise in the internal flow of an incompressible fluid having a density similar to or approaching that of surrounding structures. This phenomenon is generally not observed in problems pertaining to aeroelasticity due to relatively higher densities of solids compared to fluids. However, it carries noteworthy significance for diverse fields, including cardiovascular biomechanics, which deals with solids representing arteries engaging with blood as the fluid domain. The added mass effect is an important consideration in FSI simulations as it influences the dynamics and behavior of the coupled fluid-structure system.

Strongly coupled methods necessitate achieving convergence of the fluid and solid variables at the boundary [41]. Despite requiring iterative procedures for convergence, they yield results that can be equally matched to non-partitioned strategies. Nevertheless, these techniques may encounter complications from an “added mass effect”, leading to a non-convergence of the solution. Consequently, specialized stabilization techniques have to be engineered with the intention of mitigating its impact and broadening their potential uses concerning FSI [42]. A compilation describing different feasible couplings for FSI is shown in Figure 3.

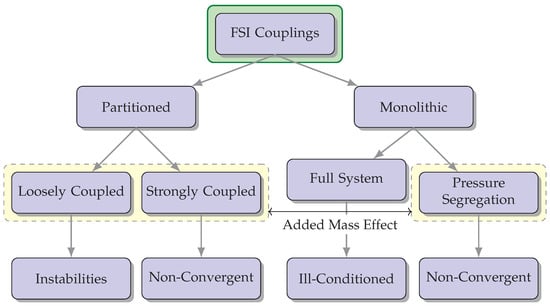
Figure 3. The diagram illustrates various possible combinations for FSI couplings and highlights potential concerns associated with each option. The incorporation of the “added mass effect” is a crucial factor to be taken into account during FSI simulations, as it has a significant impact on the dynamics and behavior of the interconnected fluid-structure system.

This entry is adapted from the peer-reviewed paper 10.3390/biology12071026

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.