You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 1 by Ningyuan Zhang and Version 3 by Camila Xu.
The cable-supported grid structure (CSGS) is a hybrid structure combined with rigidity and flexibility. Its formed state is closely related to the zero-stress state, construction process, and prestress distribution.
- cable-supported grid structure
- force-finding
- zero-stress state form-finding
1. Cable-SupporInted Grid Structuresroduction
Cable-supported grid structure (CSGS) is an emerging structure that combines rigidity and flexibility, similar to the suspendome [1][2][1,2]. The difference between them is that CSGS generally has an opening in the center of the structure. It is composed of the upper rigid grid, providing rigid support and reducing the flexibility [3], and the lower cable-strut system, which effectively increases the structural span and takes full advantage of material strength [4]. CSGS can obtain the geometric stiffness and the bearing capacity by applying the prestress in the cables, which is identical to other flexible structures. There is a compression ring in the upper rigid grid to supply constraints. The compression ring in CSGS can be assigned to three categories in accordance with its position: external compression ring, internal compression ring, and upper grid as a whole as a compression ring, as shown in Figure 1. Due to its tremendous advantages of light weight, good aesthetic, large-span high bearing efficiency, and good economy, CSGS has gradually aroused widespread attention in the engineering field, especially in the applications of the stadium [5][6][5,6]. In comparison, few projects adapt CSGS with an internal compression ring.
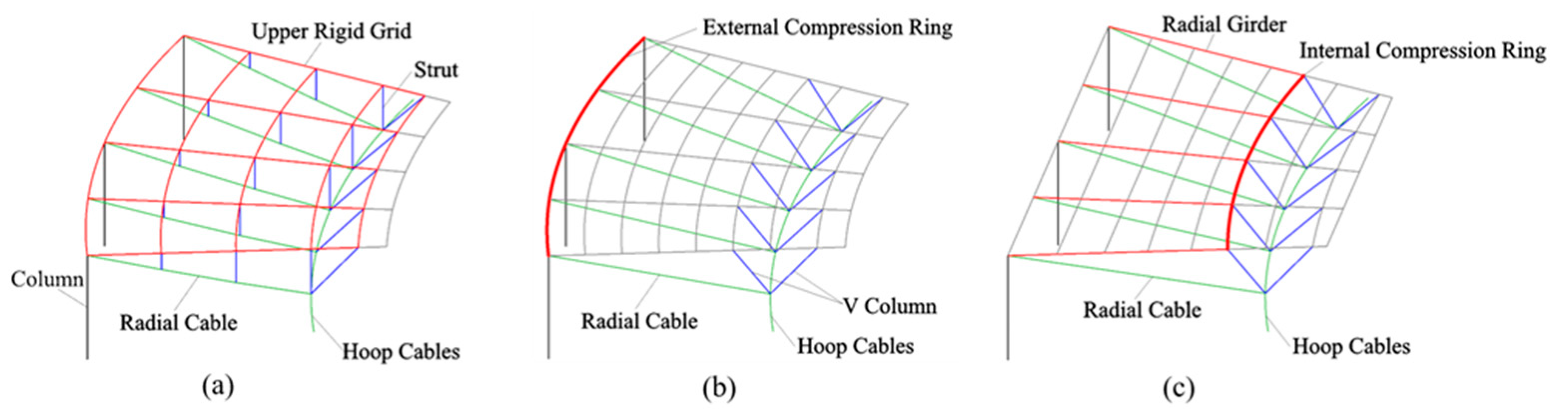

Figure 1. Three categories of CSGS: (a) upper grid as a whole compression ring; (b) external compression ring; (c) internal compression ring.
In contrast to rigid structures, the configuration of CSGS changes significantly during the construction process. Structural configuration is unstable and dynamic in the construction stage until the design configuration is reached [7]. For CSGS, it is important to find equilibrium configuration and feasible prestress distribution [8][9][8,9]. Therefore, it is an essential issue to find a stable self-equilibrium configuration in the design of various structures, including cable-net structures [10][11][12][10,11,12], cable-membrane structures [13][14][15][16][13,14,15,16], tensegrities [17][18][19][20][21][17,18,19,20,21], compressive structures [22], suspension bridges [23][24][23,24], and even submerged floating tunnels [25]. As a consequence, form-finding is a research hotspot and has been intensively studied by many scholars. The form-finding methods can be classified into two types: physical hanging models and numerical form-finding methods. The physical hanging model is used to establish a physical model to determine the structural equilibrium state under external loads [26]. Among numerous numerical form-finding methods, the force density method, dynamic relaxation method, and nonlinear finite element method are preponderant. The force density method, first put forward by Linkwitz and Scheck [27][28][27,28], defined the ratio of the internal force of components to its corresponding length as the force density, linearizing the nonlinear equations, which is concise and effective. Later researchers also devoted considerable efforts to the force density method [10][29][30][10,29,30]. The dynamic relaxation method transforms a nonlinear static problem into a pseudodynamic one [22] with fictitious mass and damping to calculate the structural equilibrium state, which is proposed by Otter [31] and Day [32]. Barnes [33] introduced the dynamic relaxation method into the form-finding analysis of cable-net and membrane structures. The nonlinear finite element method [34] applies the finite element method [35][36][35,36] to nonlinear form-finding analysis and solves nonlinear equations by iteration [37]. In addition to the three numerical methods mentioned above, the evolutionary and intelligent form-finding method has been developed to seek specific equilibrium configurations, genetic algorithms [38][39][38,39], group theory [40], particle swarm optimization algorithms [41][42][41,42], and the Monte Carlo method [43].
The configuration of CSGS can be defined as the following three states: the zero-stress state is the state before applying prestress where the structure is lofted; the prestress state, also known as the initial state, is the self-equilibrium state under its self-weight and prestress [44]; the load state refers to the state in which external loads are applied to the structure in the prestress state. The above form-finding methods generally only pay attention to the equilibrium configuration in the prestress state. Nevertheless, it is indispensable to determine the zero-stress state in practical engineering and the basis and starting point for subsequent construction steps, which will profoundly impact on the prestress state and the load state. If the prestress state is improperly taken as the starting point of the forming process, the formed structure will deviate from the design requirements, i.e., the configuration “drift” phenomenon [13]. The “drift” has less influence on small-scale structures with a low prestress level. However, it cannot be neglected and is inevitable to solve this problem for large-scale structures with a high prestress level and high precision requirements [45]. Structural components should be processed and assembled in accordance with the configuration of the zero-stress state.
In actual projects, the desired structural configuration is determined by architects or clients in general [21]. Prestress distribution in the desired structural configuration still needs further discussion in theory. Consequently, form-finding problems turn into force-finding problems when the shapes are given in advance [40], because “force” interacts with “form”. Pellegrino and Calladine [46][47][48][46,47,48] proposed the singular value decomposition (SVD) technique to obtain the self-stress modes of cable-strut structures. Yuan and Dong [49] introduce the state of integral feasible prestress to the optimal prestress design. Then, Yuan [50] proposed a general method, referred to as the double singular value decomposition (DSVD), to determine the prestress modes of cable domes. Chen and Dong [9] obtain multioverall self-stress modes from the equilibrium matrix with SVD. Many scholars have also carried out further research on force-finding [20][39][40][51][20,39,40,51].
The forming process of CSGS is also called the construction process. The construction process is the bridge between the zero-stress state and the prestress state [21]. Valid and rational construction techniques can guarantee the accuracy of prestress distribution and configuration of the formed structure [52]. The structural state of CSGS during the construction process, where the structural configuration and internal force are constantly changing, could be strikingly different from that in the service stage [3]. Hence, it is considerable to track the structural state during the construction process so as to ensure structural safety, which sets higher requirements for form-finding and force-finding in the construction stage. Construction analysis can be divided as follows: direct analysis is to analyze structural displacement and internal force during the construction process in conformity to the actual construction sequence [53]; inverse analysis takes the prestress state as the construction starting point and removes the components step by step to obtain the structural behavior in the construction stage [54]. Moreover, Luo [55] proposed the nonlinear dynamic finite element method to solve form-finding problems of the cable-strut system during the construction process. The ideal control parameters of each construction step can be determined by analysis to adjust the structural state so that the formed state is consistent with the design state.
2. Engineering Background of Cable-Supported Grid Structures
Pudong Football Stadium is the world’s first engineering application of a large-span CSGS with an internal compression ring. It is located in Shanghai, China, with a total construction area of 13,500 m2 and a 33,000 seat capacity. The structural plane is a rounded rectangle, and there are straight lines on the boundary. The long axis of the stadium is 211 m and the short axis is 173 m, as shown in Figure 2. The roof structure is about 11.8 m in height. There are 46 radial cables in total, of which the diameter of the radial cables at the corner is 110 mm and 120 mm, and those on the long side and short side are 95 mm and 110 m, respectively. The hoop cables are arranged in parallel with eight cables with a diameter of 100 mm. As a combination of rigid and flexible structures, CSGS is shaped by tensioning the lower radial cables so that it has the ability to bear loads itself. The primary constituent unit of the structure is composed of radial cable, radial girder, internal compression ring, V column outer branch, and hoop cables, forming the prestress self-balancing triangle area, as shown in Figure 2e. The specifications of the main steel components are listed in Table 1.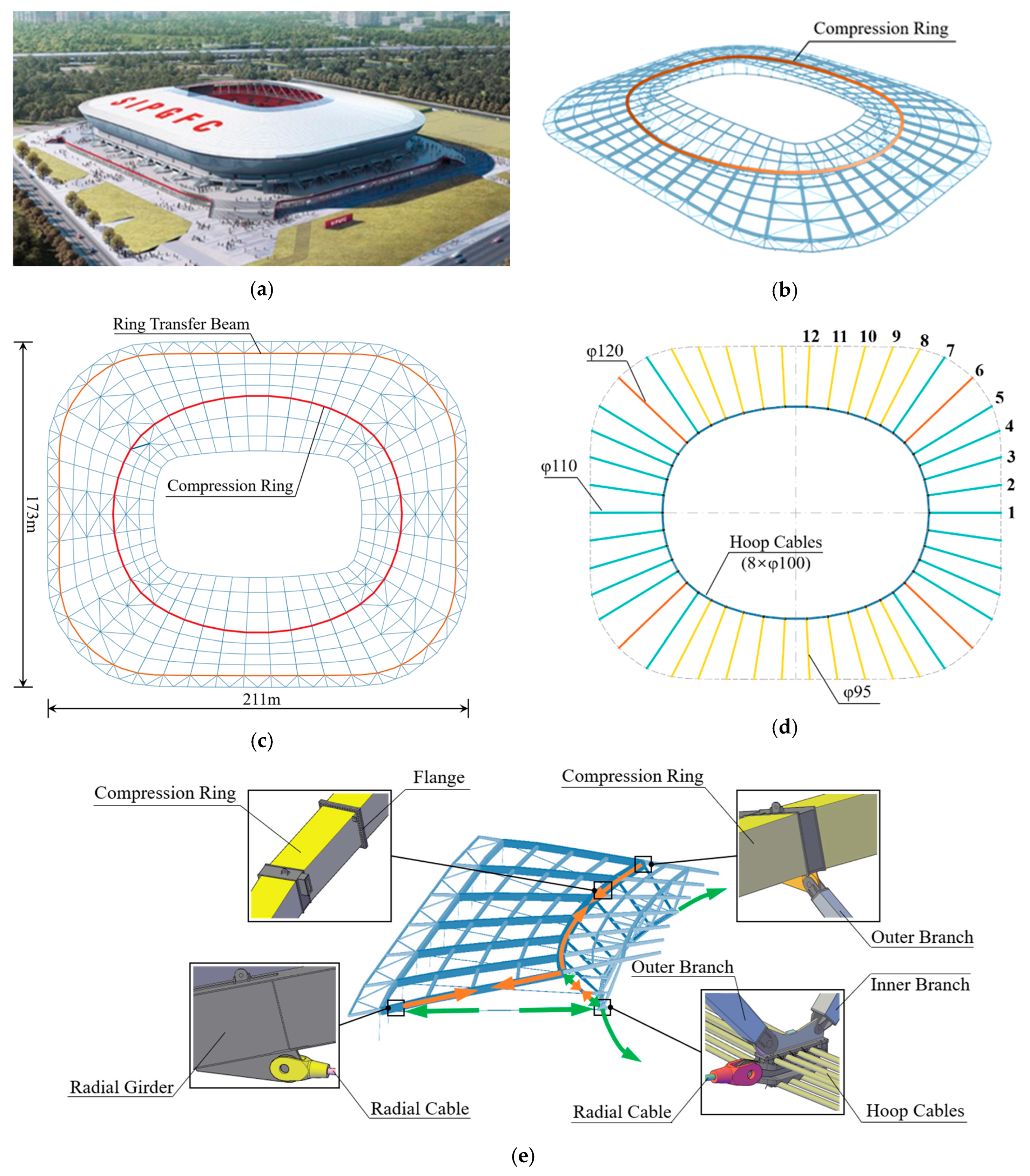
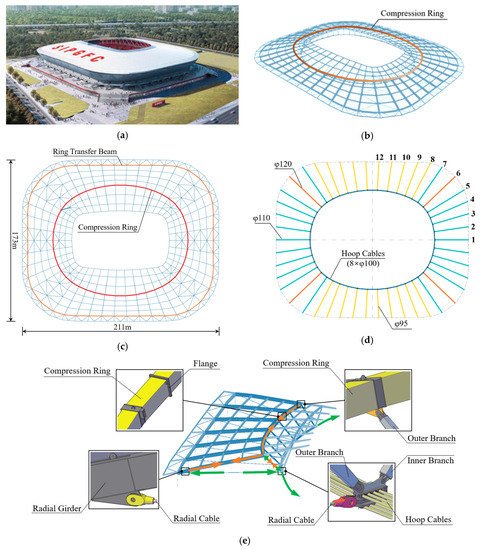
Figure 2. Schematic of Pudong Football Stadium: (a) effect picture; (b) three-dimensional view; (c) plan view; (d) radial cable distribution; (e) node detail diagram.
Table 1.
Component specifications.
| Section Type | Component | Sectional Dimension (mm) |
|---|---|---|
| Rectangular tube | Internal compression ring | 1500 × 1500 × 50 × 50 |
| Radial girder | 650 × 650 × 14 × 22 | |
| Ring beam | 1400 × 700 × 10 × 48 | |
| V column | 600 × 350 × 12 × 12 | |
| Circular tube | Column | 400 × 10 |
