1. Introduction

In recent years, lasers operating in the 1.7 μm band (1650–1750 nm) have received much attention due to the growing number of promising applications, such as bioimaging, gas detection, medical treatment, and mid-infrared laser generation. Compared with other types of lasers, 1.7 μm fiber lasers have been more intensively studied due to good stability, compactness, and beam quality. However, reported works mainly involve 1.7 μm continuous-wave (CW) fiber lasers ^[1][2][1,2], and the pulsed fiber lasers operating in this wavelength region have not been researched fully, though they have unique advantages in some applications. For example, in bioimaging applications such as multiphoton microscopy ^[3][4][3,4], optical coherence tomography [5], and spectroscopic photoacoustic (PA) imaging ^[6][7][6,7], 1.7 µm pulsed lasers can be used to realize three-dimensional (3D) volumetric imaging by time-resolved ultrasonic detection [7]. Similarly, in methane detection, the 3D distribution of the CH₄ concentration in space can be measured by using the time-of-flight ranging method to analyze the temporal characteristics of pulsed lasers when the pulsed lasers are in the 1.7 μm band used as the detection signal [8]. In fact, whether in bioimaging or gas detection, high-power 1.7 μm pulsed lasers are conducive to achieving higher sensitivity and deeper penetration/detection ^[7][9][7,9]. Thus, it is important and necessary to increase the output power of 1.7 μm pulsed fiber lasers.

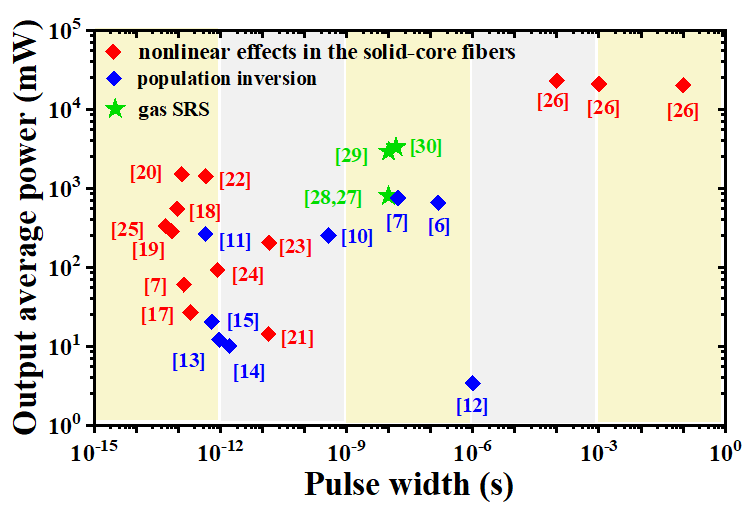
The traditional methods of realizing 1.7 μm pulsed fiber lasers can be mainly classified into two categories. One is based on population inversion to generate 1.7 μm pulsed lasers by using rare-earth-doped fibers, such as thulium-doped fibers ^{[6][7][10][11]}[6,7,10,11], thulium–holmium-codoped fibers ^[12][13][12,13], and bismuth-doped fibers ^[14][15][16][14–16]. The other is based on nonlinear effects in solid-core fibers to realize a frequency conversion, such as soliton self-frequency shift ^{[17][18][19][20]}[17–20], four-wave mixing ^[21][22][23][21–23], self-phase modulation ^[7][24][25][7,24,25], and stimulated Raman scattering (SRS) [26]. Recently, fiber gas Raman lasers (FGRLs) based on hollow-core photonic crystal fibers (HC-PCFs) have opened a new opportunity for 1.7 μm pulsed fiber lasers ^{[27][28][29][30]}[27–30]. The principle of FGRLs is to realize a frequency conversion by gas SRS in HC-PCFs. The output average powers and corresponding pulse widths of reported 1.7 μm pulsed fiber lasers are plotted in Figure 1.

Figure 1. The output average powers and corresponding pulse widths of reported 1.7 μm pulsed fiber lasers.

It can be seen that the pulse widths of 1.7 μm pulsed lasers based on solid-core fibers are mostly in femtosecond and picosecond regions and their output average powers are mostly less than 1 W. Only a pulsed Raman fiber laser can achieve an output power of up to 23 W [26], but its pulse width is at the millisecond level. Thus, it is very challenging to obtain high-power 1.7 μm pulsed lasers with a short pulse width based on solid-core fibers. The 1.7 μm FGRLs fill this gap and achieve nanosecond pulsed lasers with an output average power of over 3 W [30]. In fact, 1.7 μm nanosecond short pulsed lasers have more advantages in bioimaging. To realize volumetric imaging with higher resolution, the pulse duration should be around 10 ns or even shorter [7]. Furthermore, 1.7 μm FGRLs with continuous wavelength tunability and narrow linewidth also have more advantages in gas detection. Continuous wavelength tunability is conducive to the detection of different kinds of gas molecules, and narrow-linewidth pulsed lasers can not only accurately distinguish the absorption peaks but also have a longer coherent distance that is helpful in long-distance detection [9]. Therefore, compared with traditional 1.7 μm pulsed fiber lasers, 1.7 μm FGRLs have unique advantages and strong competitiveness due to the characteristics of high power, high efficiency, continuous wavelength tunability, and a narrow linewidth.

2. Hollow-Core Photonic Crystal Fibers

HC-PCFs are the core components of FGRLs, which provide a platform for the interaction of laser and gas. The fiber core of an HC-PCF is an air hole, so the refractive index of the fiber core is less than that of the fiber cladding and the law of total reflection is not suitable for HC-PCFs. According to the light guide mechanism, there are two major classifications of HC-PCFs, namely photonic bandgap hollow-core fibers (PBG-HCFs) ^{[31][32][33][34][35]} [31–35] and anti-resonance hollow-core fibers (AR-HCFs) (or inhibited-coupling fibers) ^{[36][37][38][39][40][41][42][43][44][45][46][47][48][49]}[36–49].

2.1. Photonic Bandgap Hollow-Core Fibers

In 1999, Russell et al. demonstrated the first PBG-HCFs [31], the schematic cross section of which is shown in Figure 2a. It can be seen that the fiber core is a larger air hole and periodic small air holes are distributed in the cladding of the PBG-HCFs. These periodic air holes in the cladding form a two-dimensional photonic bandgap, so light cannot pass through the cladding and be confined in the fiber core when the wavelength of light is located in the photonic bandgap. Since then, HC-PCFs have been developed toward lower loss and greater bandwidths. In 2004, the University of Bath demonstrated low-loss PBG-HCFs of 1.72 dB/km at 1565 nm [32], the schematic cross section of which is shown in Figure 2b. In 2005, they further reduced the fiber loss to 1.2 dB/km at 1620 nm [33], which is currently the lowest loss of PBG-HCFs. Figure 2c shows the schematic cross section of PBG-HCFs with a broad transmission band and low loss demonstrated by the Beijing University of Technology in 2019 [34]. The minimum loss of 6.5 dB/km at 1633 nm and a 3 dB bandwidth at 458 nm were achieved, which is the broadest bandwidth in PBG-HCFs. The main factors affecting the loss of PBG-HCFs are the scattering caused by the surface roughness of the fiber core boundary [33] and the coupling between the core and the surface modes [35]. Moreover, the coupling also causes multiple loss peaks in the transmission band, affecting the transmission bandwidth of the PBG-HCFs.

Figure 2. The schematic cross section of HC-PCFs. (a) The first PBG-HCF [31], (b) low-loss PBG-HCF [32], and (c) broadband PBG-HCF [34].

2.2. Anti-resonance Hollow-Core Fibers

The Kagome HCFs reported in 2002 are the first AR-HCFs ^[36] [36], the schematic cross section of which is shown in Figure 3a. Compared with PBG-HCFs, the cladding structure pitch of Kagome HCFs is larger, which can widen the optical transmission band [37]. Furthermore, there is no complete photonic bandgap in the Kagome hollow fiber, and its light-guiding mechanism can be explained by inhibited coupling [38] or the anti-resonant reflection optical waveguide (ARROW) [39]. According to the inhibited-coupling mechanism, a core-guide mode can be strongly inhibited from channeling out through the cladding by a mismatch between the core and cladding modes [40]. According to ARROW, the microstructure in the cladding is similar to a Fabry–Perot cavity. The light that meets the cavity resonance conditions will leak out through the cladding, while the light that cannot resonate in the cavity is prevented from leaking from the cladding and confined to the fiber core [41]. Figure 3b shows the schematic cross section of hypocycloid Kagome HCFs, and the design of the fiber core boundary with negative curvature reduces the transmission loss of the fiber [42]. With further study of the light-guiding mechanism of AR-HCFs, it has been found that the transmission performance of AR-HCFs is mainly determined by the first ring microstructure of the fiber core boundary. Subsequently, AR-HCFs with simpler microstructures and better optical performance have emerged ^{[43][44][45][46][47][48][49]}[43–49], and all of these AR-HCFs obey the ARROW guiding mechanism. Figure 2c presents the schematic cross section of the first tube-structure AR-HCFs reported in 2011, the cladding of which is composed of single-ring tubes [44]. The attenuation of the single-ring AR-HCFs in the mid-infrared band is much lower than that of the silica glass solid-core fiber. Figure 3d shows the schematic cross section of ice-cream-type AR-HCFs ^[44][45], the transmission band of which is located in the mid-infrared band and the minimum loss of which is 34 dB/km at 3050 nm. With further study of AR-HCFs, it has been found that the touching points of adjacent capillaries in the cladding behave as independent waveguides supporting their own lossy modes, which would introduce additional transmission loss ^[50][51][50,51]. Thus, nodeless single-ring AR-HCFs were first demonstrated in 2013 [46]. In addition, it was demonstrated that the elimination of the tube’s contact point helps to reduce the bending loss [47]. In 2019, nodeless nested AR-HCFs with the attenuation of 0.65 dB/km in the C and L telecommunications bands were demonstrated, which means this was the first time that HC-PCFs realized a loss comparable to that of silica glass solid-core fibers [48]. The attenuation of nodeless nested AR-HCFs was further recued to 0.28 dB/km in 2020 [49].

Compared with PBG-HCFs, the mode field of AR-HCFs overlaps the silica glass of the fiber core boundary less [52]. Thus, the surface scattering loss of AR-HCFs is lower than that of PBG-HCFs, which means that AR-HCFs have advantages of realizing lower loss and reducing the nonlinearities caused by silica glass. Furthermore, although both AR-HCFs and PBG-HCFs are multimode, the attenuation of high-order modes in AR-HCFs is higher than that of PBG-HCFs, which means that with AR-HCFs it is easier to obtain a fundamental mode guidance at a short fiber length [53].

Figure 3. The schematic cross section of HC-PCFs. (a) The first AR-HCF [36], (b) hypocycloid Kagome AR-HCFs [42], (c) single-ring AR-HCFs [44], (d) ice-cream-type AR-HCF [45], (e) nodeless single-ring AR-HCFs [46], and (f) nodeless nested AR-HCFs [48].

References

1. Burns, D.; Shardlow, P.C.; Barua, P.; Jefferson-Brain, T.L.; Sahu, J.K.; Clarkson, W.A. 47 W continuous-wave 1726 nm thulium fiber laser core-pumped by an erbium fiber laser. Opt. Lett. 2019, 44, 5230–5233.
2. Zhang, ; Song, J.; Ye, J.; Xu, J.; Yao, T.; Zhou, P. Tunable random Raman fiber laser at 1.7 μm region with high spectral purity. Opt. Express 2019, 27, 28800–28807.
3. Cheng, ; Tong, S.; Deng, X.; Liu, H.; Du, Y.; He, C. Deep-brain 2-photon fluorescence microscopy in vivo excited at the 1700 nm window. Opt. Lett. 2019, 44, 4432–4435.
4. Horton, G.; Xu, C. Dispersion compensation in three-photon fluorescence microscopy at 1,700 nm. Biomed. Opt. Express 2015, 6, 1392–1397.
5. Kawagoe, ; Ishida, S.; Aramaki, M.; Sakakibara, Y.; Omoda, E.; Kataura, H. Development of a high-power supercontinuum source at the 1.7 μm wavelength region for highly penetrative ultrahigh-resolution optical coherence tomography. Biomed. Opt. Express 2014, 5, 932–943.
6. Li, ; Shi, J.; Gong, X.; Kong, C.; Luo, Z.; Song, L. 1.7 μm wavelength tunable gain-switched fiber laser and its application to spectroscopic photoacoustic imaging. Opt. Lett. 2018, 43, 5849–5852.
7. Li, ; Shi, J.; Wang, X.; Wang, B.; Gong, X.; Song, L. High-energy all-fiber gain-switched thulium-doped fiber laser for volumetric photoacoustic imaging of lipids. Photonics Res. 2020, 8, 160–164.
8. Li, ; Zheng, C.; Liu, H.; He, Q.; Ye, W.; Zhang, Y.; Pan, J.; Wang, Y. Development and measurement of a near-infrared CH₄ detection system using 1.654 μm wavelength-modulated diode laser and open reflective gas sensing probe. Sens. Actuators B Chem. 2016, 225, 188–198.
9. Yin, ; Qi, Z.; Chen, F.; Song, Y.; He, S. High peak-power and narrow-linewidth all-fiber Raman nanosecond laser in 1.65 μm waveband. Opt. Express 2020, 28, 7175–7181.
10. Li, ; Kong, C.; Wong, K.K.Y. High Energy Noise-Like Pulse Generation from a Mode-Locked Thulium-Doped Fiber Laser at 1.7 μm. IEEE Photonics J. 2019, 11, 1–6.
11. Li, ; Wei, X.; Kong, C.; Tan, S.; Chen, N.; Kang, J. Fiber chirped pulse amplification of a short wavelength mode-locked thulium-doped fiber laser. APL Photonics 2017, 2, 121302.
12. Du, ; Ruan, Q.; Yang, R.; Li, W.; Wang, K.; Luo, Z. 1.7-μm Tm/Ho-Codoped All-Fiber Pulsed Laser Based on Intermode-Beating Modulation Technique. J. Lightwave Technol. 2018, 36, 4894–4899.
13. Noronen, ; Okhotnikov, O.; Gumenyuk, R. Electronically tunable thulium-holmium mode-locked fiber laser for the 1700-1800 nm wavelength band. Opt. Express 2016, 24, 14703–14708.
14. Noronen, ; Firstov, S.; Dianov, E.; Okhotnikov, O.G. 1700 nm dispersion managed mode-locked bismuth fiber laser. Sci. Rep. 2016, 6, 24876.
15. Khegai, ; Melkumov, M.; Riumkin, K.; Khopin, V.; Firstov, S.; Dianov, E. NALM-based bismuth-doped fiber laser at 1.7 μm. Opt. Lett. 2018, 43, 1127–1130.
16. Thipparapu, K.; Wang, Y.; Wang, S.; Umnikov, A.A.; Barua, P.; Sahu, J.K. Bi-doped fiber amplifiers and lasers [Invited]. Opt. Mater. Express 2019, 9, 2446–2465.
17. Fang, ; Wang, Z.Q.; Zhan, L. Efficient generation of all-fiber femtosecond pulses at 1.7 μm via soliton self-frequency shift. Opt. Eng. 2017, 56, 046107.
18. Nguyen, N.; Kieu, K.; Churin, D.; Ota, T.; Miyawaki, M.; Peyghambarian, N. High Power Soliton Self-Frequency Shift with Improved Flatness Ranging From 1.6 to 1.78 μm. IEEE Photonics Technol. Lett. 2013, 25, 1893–1896.
19. Wang, ; Xu, C. Tunable high-energy soliton pulse generation from a large-mode-area fiber and its application to third harmonic generation microscopy. Appl. Phys. Lett. 2011, 99, 071112.
20. Zach, ; Mohseni, M.; Polzer, C.; Nicholson, J.W.; Hellerer, T. All-fiber widely tunable ultrafast laser source for multimodal imaging in nonlinear microscopy. Opt. Lett. 2019, 44, 5218–5221.
21. Becheker, ; Tang, M.; Hanzard, P.H.; Tyazhev, A.; Mussot, A.; Kudlinski, A. High-energy dissipative soliton-driven fiber optical parametric oscillator emitting at 1.7 μm. Laser Phys. Lett. 2018, 15, 115103.
22. Qin, ; Batjargal, O.; Cromey, B.; Kieu, K. All-fiber high-power 1700 nm femtosecond laser based on optical parametric chirped-pulse amplification. Opt. Express 2020, 28, 2317–2325.
23. Tang, ; Becheker, R.; Hanzard, P.H.; Tyazhev, A.; Oudar, J.L.; Mussot, A. Low Noise High-Energy Dissipative Soliton Erbium Fiber Laser for Fiber Optical Parametric Oscillator Pumping. Appl. Sci. 2018, 8, 2161–2175.
24. Zeng, ; Akosman, A.E.; Sander, M.Y. Supercontinuum Generation from a Thulium Ultrafast Fiber Laser in a High NA Silica Fiber. IEEE Photonics Technol. Lett. 2019, 31, 1787–1790.
25. Chung, Y.; Liu, W.; Cao, Q.; Kartner, F.X.; Chang, G. Er-fiber laser enabled, energy scalable femtosecond source tunable from 1.3 to 1.7 μm. Opt. Express 2017, 25, 15760–15771.
26. Grimes, ; Hariharan, A.; Sun, Y.; Ovtar, S.; Kristensen, P.; Westergaard, P.G.; Rako, S.; Baumgarten, C.; Stoneman, R.C.; Nicholson, J.W.; et al. Hundred-watt CW and Joule level pulsed output from Raman fiber laser in 1.7-μm band. In Proceedings of the SPIE 11260, Fiber Lasers XVII: Technology and Systems, San Francisco, CA, USA, 21 February 2020.
27. Cui, ; Huang, W.; Li, Z.; Zhou, Z.; Wang, Z. High-efficiency laser wavelength conversion in deuterium-filled hollow-core photonic crystal fiber by rotational stimulated Raman scattering. Opt. Express 2019, 27, 30396–30404.
28. Huang, ; Li, Z.; Cui, Y.; Zhou, Z.; Wang, Z. Efficient, watt-level, tunable 1.7 µm fiber Raman laser in H₂-filled hollow-core fibers. Opt. Lett. 2020, 45, 475–478.
29. Li, ; Huang, W.; Cui, Y.; Zhou, Z.; Wang, Z. 3 W tunable 1.65 µm fiber gas Raman laser in D₂-filled hollow-core photonic crystal fibers. Opt. Laser Technol. 2020, 132, 106474.
30. Li, ; Pei, W.; Huang, W.; Cui, Y.; Wang, M.; Wang, Z. Highly efficient nanosecond 1.7 μm fiber gas Raman laser by H₂-filled hollow-core photonic crystal fibers. Crystals 2021, 11, 32.
31. Cregan, Mangan, Knight, Birks, Russell, Roberts, Single-Mode Photonic Band Gap Guidance of Light in Air. Science 1999, 285, 1537–1539.
32. Mangan, J.; Farr, L.; Langford, A.; Roberts, P.J.; Williams, D.P.; Couny, F.; Lawman, M.; Mason, M.; Coupland, S.; Flea, R. Low loss (1.7 dB/km) hollow core photonic bandgap fiber. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22 February 2004.
33. Roberts, J.; Couny, F.; Sabert, H.; Mangan, B.J.; Russell, P.S.J. Ultimate low loss of hollow-core photonic crystal fibres. Opt. Express 2005, 13, 236–244.
34. Zhang, ; Gao, S.; Wang, Y.; Ding, W.; Wang, X.; Wang, P. 7-cell hollow-core photonic bandgap fiber with broad spectral bandwidth and low loss. Opt. Express 2019, 27, 11608–11616.
35. Smith, M.; Venkataraman, N.; Gallagher, M.T.; Muller, D.; West, J.A.; Borrelli, N.F.; Allan, D.C.; Koch, K.W. Low-loss hollow-core silica/air photonic bandgap fibre. Nature 2003, 424, 657–659.
36. Benabid, ; Knight, J.C.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 2002, 298, 399–402.
37. Couny, ; Benabid, F.; Light, P.S. Large-pitch kagome-structured hollow-core photonic crystal fiber. Opt. Lett. 2006, 31, 3574–3576.
38. Couny, ; Benabid, F.; Roberts, P.J.; Light, P.S.; Raymer, M.G. Generation and photonic guidance of multi-octave optical-frequency combs. Science 2007, 318, 1118–1121.
39. Pearce, J.; Wiederhecker, G.S.; Poulton, C.G.; Burger, S. Models for guidance in kagome-structured hollow-core photonic crystal fibres. Opt. Express 2007, 15, 12680–12685.
40. Debord, ; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217.
41. Litchinitser, M.; Abeeluck, A.K.; Headley, C. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594.
42. Wang, Y.; Wheeler, N.V.; Couny, F. Low loss broadband transmission in hypocycloid-core Kagome hollow-core photonic crystal fiber. Opt. Lett. 2011, 36, 669–671.
43. Gérôme, ; Jamier, R.; Auguste, J.L. Simplified hollow-core photonic crystal fiber. Opt. Lett. 2010, 35, 1157–1159.
44. Pryamikov, D.; Biriukov, A.S.; Kosolapov, A.F.; Plotnichenko, V.G.; Semjonov, S.L.; Dianov, E.M. Demonstration of a waveguide regime for a silica hollow-core micro structured optical fiber with a negative curvature of the core boundary in the spectral region >3.5 μm. Opt. Express 2011, 19, 1441–1448.
45. Yu, ; Wadsworth, W.J.; Knight, J.C. Low loss silica hollow core fibers for 3–4 μm spectral region. Opt. Express 2012, 20, 11153–11158.
46. Kolyadin, N.; Kosolapov, A.F.; Pryamikov, A.D.; Biriukov, A.S.; Plotnichenko, V.G.; Dianov, E.M. Light transmission in negative curvature hollow core fiber in extremely high material loss region. Opt. Express 2013, 21, 9514–9519.
47. Gao, F.; Wang, Y.Y.; Liu, X.L. Bending loss characterization in nodeless hollow-core anti-resonant fiber. Opt. Express 2016, 24, 14801–14811.
48. Bradley, D.; Jasion, G.T.; Hayes, J.R. Antiresonant Hollow Core Fibre with 0.65 dB/km Attenuation across the C and L Telecommunication bands. In Proceedings of the 45th European Conference on Optical Communication, Dublin, Ireland, 26 September 2019.
49. Jasion, T.; Bradley, T.D.; Harrington, K.; Sakr, H.; Chen, Y.; Fokoua, E.N.; Davidson, I.A.; Taranta, A.; Hayes, J.R.; Richardson, D.J. Hollow Core NANF with 0.28 dB/km Attenuation in the C and L Bands. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition, San Diego, CA, USA, 8 March 2020.
50. Vincetti, ; Setti, V. Extra loss due to Fano resonances in inhibited coupling fibers based on a lattice of tubes. Opt. Express 2012, 20, 14350–14361.
51. Jaworski, ; Yu, F.; Maier, R.R.J.; Wadsworth, W.J.; Knight, J.C.; Shephard, J.D.; Hand, D.P. Picosecond and nanosecond pulse delivery through a hollow-core Negative Curvature Fiber for micro-machining applications. Opt. Express 2013, 21, 22742–22753.
52. Bufetov, A.; Kosolapov, A.F.; Pryamikov, A.D.; Gladyshev, A.V.; Kolyadin, A.N.; Krylov, A.A.; Yatsenko, Y.P.; Biriukov, A.S. Revolver Hollow Core Optical Fibers. Fibers 2018, 6, 39.
53. Komanec, ; Dousek, D.; Suslov, D.; Zvanove, S. Hollow-Core Optical Fibers. Radioengineering 2020, 29, 417–430.