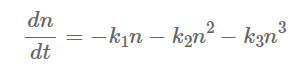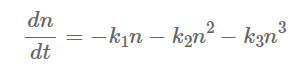Organic–inorganic hybrid perovskite solar cells (PSCs) have attracted much attention because of their advantages, such as tunable bandgap [1], high charge carrier mobility [2], high light absorption coefficient [3], and low exciton binding energy [4]. Since Miyasaka et al. [5] in 2009, the first attempt to use a halide perovskite as a sensitizer in dye-sensitized solar cell structures, PSCs have achieved remarkable progress in the last decade, with a rapid increase in power conversion efficiency (PCE) from a previously reported 3.8 percent to a current 25.7 percent [6]. Figure 1 illustrates the efficiency evolution of perovskite-type solar cells [7], which is equivalent to today’s industrial-grade single-crystal silicon solar cells. This outstanding efficiency, combined with the processing characteristics and low manufacturing cost of perovskite solutions [8], makes it a promising candidate for the next generation of thin-film solar cells.

Although PSCs have developed rapidly, their efficiency remains far below their Shockley–Queisser (SQ) maximum theoretical efficiency (>30%) [9]. The SQ limit efficiency is based on the condition that each carrier recombination is radiative; thus, to improve the PCE value, non-radiative recombination that causes energy loss must be reduced. Currently, PSCs are largely divided into planar heterojunction structures and mesoporous structures. Each structure typically includes a conductive glass/electron transport layer (ETL)/perovskite (PVK)/hole transport layer (HTL)/precious metal electrode [10]. Defects and energy level mismatch in the PVK interface (ETL/PVK interface, PVK/HTL interface) are the main sources of nonradiative recombination, which influences the final performance of the device ^[11][12][11,12]. Minimizing non-radiative recombination at the interface is crucial for PSCs with high efficiency and stability.

High efficiency solar cell materials should absorb a wide range of spectra to produce highly efficient electric charges and transfer them to electrodes with minimal losses. Carrier dynamics in PSCs include a lot, such as charge dissociation, charge transport, charge extraction, charge recombination, charge accumulation, and charge collection, as shown in Figure 23a with corresponding time scales ^[13][14][29,30]. The excitation, relaxation, and transport of carriers occur on an extremely short timescale (picosecond scale) ^[15][16][31,32]. When the photon energy is equivalent to or above the bandgap, electrons in the valence band transition to the conduction band. The interaction between excitons is called exciton binding energy, which is low in perovskites, and excitons spontaneously dissociate into free carriers upon photoexcitation ^[17][18][19][33,34,35]. In addition, some of the carriers are excited to an energy position above the conduction band minimum (CBM) and valence band maximum (VBM) or are pumped to high-energy sub-bands to form hot carriers ^[20][36]. These heat carriers are released to the CBM or VBM via electron–phonon interaction ^[21][37]. The process of free charge carrier transportation through diffusion or drift in the absorber of a perovskite typically takes several nanoseconds ^[22][23][38,39], and there are dynamic and competitive conditions between the transport and the recombination processes ^[24][25][40,41]. Charge recombination includes radiative and non-radiative recombination ^[26][42]. During radiative recombination, perovskites emit photons from the system, the size of which depends on the product of the hole concentrations and electron. Radiative recombination is inevitable, but it has subtle influence and could be ignored. The radiative recombination rate is much smaller than the non-radiative recombination rate, which consists of the Shockley-Read-Hall recombination and the Auger recombination. The transport and recombination of carriers described previously are shown in Figure 23b,c ^[27][43]. The course of non-radiative and radiative recombination can be described as follows ^[28][44]: In the equation, k1, k2, and k3 are the rate constants associated with the defect auxiliary (single particle), radiative (two-particle), and Auger (three-particle) recombination processes, respectively, and n is the density of photogenerated carriers. Defect-assisted recombination is dependent on the energy depth and density of the defect, whereas the Auger recombination mainly takes place in perovskite absorbers with high carrier concentrations ^{[29][30][31][32][33]}[45,46,47,48,49]. At the interface, minimizing defects and surface states is expected to reduce SRH recombination ^[34][50], and a larger Schottky barrier selectively extracts majority carriers and blocks minority carriers ^[35][36][51,52]. After charge dissociation and transfer, charge extraction occurs rapidly on a picosecond timescale. Charge extraction (injection) has a direct relationship with the incident photon-to-current conversion efficiency (IPCE) as well as Jsc. IPCE is defined as IPCE =η_LHE×η_inj^×ηcc, where η_LHE is the light capture efficiency, η_inj is the electron injection yield, and _^ηcc is the charge collection efficiency ^[37][53]. As discussed above, the extraction efficiency of the interface charge is primarily decided by the ELA, which relies on the location of the adjacent interface materials. Good energy level alignment can produce an appropriate built-in potential, which is beneficial for charge transfer. In general, it is believed that an energy shift of approximately 0.2 eV is required in order to ensure resultful charge extraction on the ETL/perovskite and perovskite/HTL interface ^[29][45]. Charge extraction and ion migration defects are the main causes of charge accumulation, which occurs on a time scale exceeding one second. The accumulation of charge affects electrode polarization, interface energy level mismatch, built-in electric fields, as well as back charge transfer that is near the interface ^[13][38][29,54]. In addition, it has been shown that the main source of J-V hysteresis is caused by the accumulation of interface charges from the interfacial defects and ions, rather than by ion migration in the perovskite thin film during the charge-discharge 169 dynamics ^[39][40][55,56]. After being extracted, the charges need to be collected by the electrode within a few microseconds ^[41][57]. The charge transfer efficiencies at the working electrode/ETL interface and HTL/counter electrode interface, as well as the electrode material conductivity, mainly determine the charge collection. If the base electrode is made of FTO or ITO, and the top electrode of the CTL is made of metal Au or Ag, then the efficiency of charge collecting is generally high ^[42][58]. As discussed above, charges need to be transferred through multiple layers and through two interfaces (the charge extraction and collection interfaces), which can be seen as a series circuit. From this, the overall internal quantum efficiency (IQE) of the PSCs could be deduced as IQE = , where is the charge extraction efficiency, and is the charge collection efficiency. These are determined by interface charge-carrier dynamics. To achieve a high IQE, it is necessary to have a high charge extraction as well as a low recombination rate, which in turn needs suitable interface energy structures, charge distribution, and atomic bonding ^[14][30]. Therefore, charge carrier dynamics are crucial to device performance. The high defect densities in the carrier transport layer (CTL) and the perovskite layer capture carriers, leading to interfacial non-radiative recombination, resulting in a decrease in PCE and stability. Currently, many studies pay attention to the top surface of the perovskite layer ^[43][44][14,59] because it is difficult to expose the buried interface and characterize it accurately ^[45][60]. However, the accumulation of defects is more concentrated at the buried interface than at the top interface, making the study of buried interface defects more important ^[46][61]. The delamination process proposed by Zhu et al. 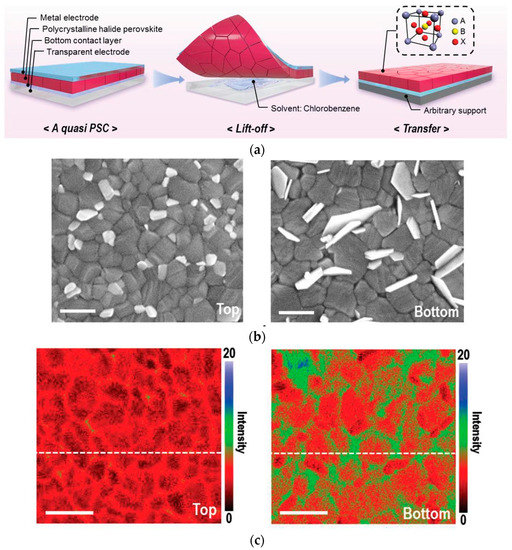^[47][18] (Figure 34a) can reveal the buried interface at the perovskite thin film. Macroscopically, combining the interface and surface characterization reveals that the losses at the buried interface are caused by sub-micron defects and inhomogeneities. SEM images show that there are more and larger lead halide plate-like particles at the bottom than at the top (Figure 34b), and further analysis using nanoscale Fourier-transform infrared spectroscopy (nano-FTIR) and PL reveal that the lateral concentration inhomogeneity of the main organic cations is more pronounced at the bottom than at the top (Figure 34c). Sub-micron defects and inhomogeneities are involved in the non-radiative recombination center, limiting the performance of the device. 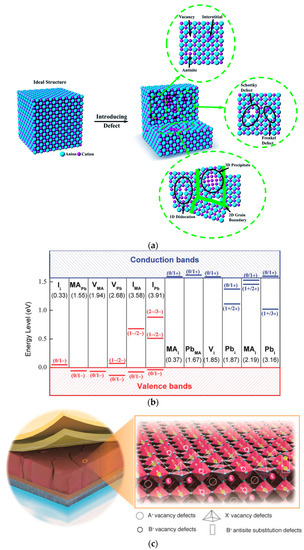From a microscopic perspective, in an ideal semiconductor crystal structure, every atom is in the right position, with no defects or impurities (Figure 45a). However, due to the solution deposition method used to prepare perovskite thin films and the subsequent rapid crystallization annealing process, a large number of unavoidable defects exist in the actual prepared semiconductor. Figure 45a shows three types of point defects (vacancies, interstitials, and antisites) ^[48][49][62,63], which can be intrinsic or introduced by foreign atoms. In addition to point defects, Figure 45a shows two types of defect pairs (Frenkel and Schottky defects) ^[50][64]. The point defects and defect pairs consist of a range of dimensional defects, as shown in Figure 45a, such as 1D defect dislocations formed along the crystal, 2D defects formed at the grain surfaces and boundaries, and 3D defects that may lead to volume changes in the crystal. The 3D defect contains precipitates (tiny volumes with various crystal structures), second phase domains, and large voids ^[51][52][65,66]. Currently, first-principles calculations are commonly used to calculate the theoretical formation energy of point defects ^[53][54][67,68]. Yin et al. ^[55][69] theoretically calculated the energy level positions of point defects within MAPbI₃, as shown in Figure 45b. Among them, most of the point defects in MAPbI₃ are shallow-level defects, where the difference between the ground-state energy level of the defect and the migration edge of the valence band or conduction band is equal to or less than the thermal excitation energy k_BT at room temperature ^[56][70]. Only I_MA, I_Pb, Pb_I, and Pb_i are deep-level defects within the perovskite bandgap, where the energy difference is larger than k_BT ^[57][71]. Deep-level defects can capture electrons or holes, which are unable to escape by thermal activation and are eliminated by carrier recombination of opposite charges. This is the main factor for non-radiative recombination ^[58][72]. Therefore, defects in polycrystalline perovskite thin film bulk have little effect on non-radiative recombination ^[56][70]. Special attention has been paid to defects in the thin film interface. Xiao et al. demonstrated the existence of a high-density trap near the surface or a grain boundary of perovskite film through photoluminescence (PL) and thermal admittance spectroscopy (TAS) ^[59][73]. Currently, common interface defects include cation vacancies, anion vacancies, and anti-site defects, as illustrated in Figure 5c ^[60][74]. Wang et al. ^[61][75] used density functional theory (DFT) to calculate the formation energies of four types of defects on the surface of perovskite thin films and compared the formation energies of these defects on the surface and inside the films. The Pb_I antisite defect is easy to form on the surface of perovskite thin films and is dominant. As a deep-level defect, the Pb_I antisite defect causes serious non-radiative recombination in the device. The results indicate that the charge trap density is 1–2 orders of magnitude higher at the interface of polycrystalline perovskite ^[46][61]. For buried interfaces studied, they generally refer to the interface in the middle of the electron transport layer and the perovskite layer, which contains abundant oxygen vacancies, hydroxyl groups, and unsaturated coordinated metal atoms ^[62][63][76,77]. Thus, defects on the surface of perovskite and the interface of PSCs are critical to the performance of the device. 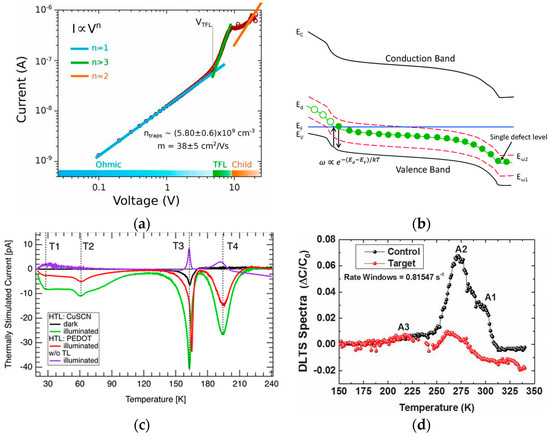Research on defect characterization techniques is required to characterize defects or defect density and energy levels. Measurement techniques such as space charge limited current (SCLC), thermally stimulated current (TSC), thermal admittance spectroscopy (TAS), steady-state photoluminescence (SSPL), and deep level transient spectroscopy (DLTS) are used for this purpose. The SCLC is often used to measure material properties such as defect density, conductivity, carrier density, and mobility ^{[64][65][66][67]}[78,79,80,81]. Although SCLC has been widely accepted for evaluating defect density in MTP, there are also some drawbacks. First of all, the SCLC can only show the density of one type of charge defect (electron trap or hole trap) at one time by means of one charge-type device. In addition, the V_TFL estimation of defect density assumes that the linear part of J-V is always present in the ohmic region until the defect is fully filled, as shown in Figure 56a ^[64][78]. However, it is also possible that the starting point is due to the field ionization of the defect or the start of the double injection effect. Therefore, there is a possibility of incorrect assumptions of the estimated defect density ^[68][82]. TAS measures defect density by tracking the capacitance change of the defect during the alternating current (AC) voltage, including deep-level defects and shallow-level defects ^{[69][70][71][72]}[83,84,85,86]. In typical PSCs, capacitance is mainly due to the discharge of charges trapped in defects under AC frequency variation. The semiconductor defect density is related to the position of the Fermi level, as shown in Figure 56b ^[72][86]. TAS is one of the most efficient methods for qualitatively comparing defect density in perovskite thin films under different conditions. However, it is only the defect traps that are lower than the energy threshold that can capture or emit electric charges and produce capacitive signals. Additionally, capture charges that are temperature-dependent and have long thermal emission times cannot lead to capacitance signals. These factors reduce the accuracy of measuring the defect density ^[69][83]. The fundamental principle of the TSC is that it is possible to partially fill the defect trap with an optically excited electron at very low temperatures. These electrons can be thermally excited to the CBM through dark heating, producing a current signal I_TSC ^[73][87]. The relationship between TSC and temperature for different devices is shown in Figure 56c ^[74][88]. However, TSC is only able to estimate the lower limit of defect density in MTP. Inaccuracies in estimation may occur due to incomplete defect filling, charge recombination, and other processes. DLTS is used to detect deep-level defects ^[75][89]. In DLTS tests, different voltage signals are applied at different temperatures to measure changes in capacitance, current (i-DLTS), or charge (Q-DLTS) over time. First, most of the mobile charge carriers are depleted by reverse-biasing the semiconductor junction. Then, the voltage is zeroed briefly by a positive voltage pulse, and the empty trap is filled. At the end of the pulse, the semiconductor junction is reverse-biased again. In this case, the movement of the charge causes a change in the transient capacitance. The defect state and the energy difference of the band edge are determined by using the variation of the defect emission rate versus temperature and the defect capture cross section. Figure 56d shows DLTS spectra of perovskite films before and after I₃⁻ passivation ^[76][90]. For instance, it could miss some charge trapped in defects that are not filled under forward bias. Additionally, if the emission rate of the thermal is quite larger than that of optical emission, then the transient disappears as the defects are no longer filled between pulses. This shows that the DLTS is not capable of detecting shallow defects with high thermal emission rates. In order to make up for the shortcomings of different characterization methods, characterization techniques are often combined. Meggiolaro et al. ^[77][91] utilized first-principle calculations (DFT) and high-sensitivity photoluminescence and transient absorption measurements to determine the origin of defects. Stecker et al. ^[78][92] explored the surface defect properties and a few defect types (at atomic scale) by combining DFT calculation with STM ^[79][93]. There are also some indirect methods. Yang et al. ^[80][94] used the Lewis acid passivation effect to distinguish between halide defects and Pb defects, with the former being more pronounced. The existence of trap states on the surface of Pb⁰ was determined by Zu et al., using XPS and UPS ^[81][95]. Although there have been many successful cases, it is still very difficult to accurately identify and quantitatively detect defects.