
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Andre Vatarescu | + 4118 word(s) | 4118 | 2019-07-23 09:53:38 | | | |
| 2 | Andre Vatarescu | + 4123 word(s) | 4123 | 2019-07-28 10:50:35 | | | | |
| 3 | Bruce Ren | -997 word(s) | 3126 | 2020-10-28 08:57:04 | | |
Video Upload Options
The interpretation of published experimental results intended to prove the existence of a quantum phenomenon of non-locality involving photonic entangled states did not take into consideration the existence of the quantum Rayleigh conversion of photons in dielectric media. This phenomenon leads to the existence of high levels of correlations between two independent photonic and linearly polarized quantum states generated after the entangled photons have been absorbed through the quantum Rayleigh conversion. Both pure and mixed individual states of polarization result in expressions normally associated with entangled photonic states, providing support for the view that the physical reality of quantum non-locality is highly questionable.
1. Introduction
Over the past half-century, large amounts of resources have been invested in experiments based on photonic devices in order to prove the existence of the quantum non-locality by measuring expectation values of detected polarized photons that comply with various versions of Bell inequalities [1][2][3][4][9][10][11][12][13][14]. For some unexplained reason, from a scientific perspective, it has always been assumed that no other external or additional physical processes could take place in the experimental configurations. Yet, over the years, questions have emerged about the validity of the experimental model, from different directions [5][6]. The supporters of the theory of quantum non-locality [7] choose to ignore or denigrate these objections without addressing them directly [8].
The concept of quantum non-locality in the context of photonic systems would cause a measurement carried out at location A to influence a measurement performed at location B. The requirement for this effect to take place is that the two photons – measured separately – had a joint interaction which left them correlated or in an entangled state. This combination of quantum non-locality and entanglement of photons would, allegedly, result in strongly correlated measurement outcomes [1].
The relatively strong correlations between the detected states of polarizations of the two space-time separated photons [1] were considered to be a clear indication of an instantaneous collapse into an eigenstate of the wave function describing the two apparently entangled photons and, as a result, it was concluded that a non-local mechanism - of an yet unknown origin and nature - brings about a mutual influence between the two distant measurements. Overall, it is argued that those correlations disprove beyond any doubt the paradox pointed out by Einstein, Podolsky and Rosen (EPR), while complying with the uncertainty principle for each subsystem which would not allow simultaneous sharp values for two incompatible variables linked to the Pauli spin operators which do not commute.
The measured events of correlated pairs of photons are “extremely rare” [1], with typical values of “slightly more than one event-ready signal per hour” [2]. Nevertheless, the interpretation of the experimental results of [1][2][3][4] failed to take into account the role played by the quantum Rayleigh conversion of photons [9][10][11][12][13][14] in their propagation through the dielectric media of optical fibers, beam splitters, polarization rotating devices and other dielectric elements comprising the experimental setups. While the classical Rayleigh scattering induced by perturbations of the refractive index is the major loss factor in optical fibers [15], the quantum Rayleigh conversion of photons has been practically ignored although documented in early textbooks [9][10].
In the case of only one photon propagating through a dielectric medium, the only process occurring is that of absorption of the photon by an oscillating dipole and spontaneous emission of one photon, which corresponds to the quantum Rayleigh conversion of photons (QRCP) which is outlined in Appendix A.
This article analyses the physical process of quantum Rayleigh scattering of photons through spontaneous emission which is bound to affect the propagation of the single photons originating from the same source and forming the components of entangled states [1][2][3][4] . Correlation functions - evaluated in Section 2 - are associated with the two independently and separately emitted qubits of photons, and deliver the same degree of high correlations for pure states and variable outcomes for mixed states. Additionally, each term of the commutative relations between the relevant Pauli operators in the context of the individual and separated photonic state vectors will vanish leading to the possibility of simultaneous measurements and the absence of an EPR paradox. The implications of replacing the physically eliminated entangled states of photons with individual and independent qubits are discussed in Section 3 and support the view of reference [14] objecting to the existence of quantum nonlocality. The conclusions summarizing the main results of this article point out the feasibility of explaining the published experimental - apparently supporting the concept of quantum nonlocality- by adopting a fully local approach based on a well-established physical process.
2. Correlation functions
As a photon enters a birefringent crystal and interacts with electric dipoles, the photon needs to be re-emitted into a polarization eigenstate so it can propagate in the same forward direction to reach the intended photodetector. If each of the individual photons of the initial pair is re-emitted into their original state of polarization and reaches its respective detector within the designated time interval for a coincidence count to be registered, then this physical process can be mistaken for the physically impossible case of the entangled photons having survived their propagation through the dielectric media without interacting with electric dipoles. Nevertheless, as photons acquire a phase shift as a results of their propagation, the probability of no dipole-photon interactions taking place even for a short distance of millimetres, is nil.
2.1 Pure states of polarization
Although the conventional definition of the correlation function – see [16] (Eq.13) – involves the same state of polarization reaching the two separate detectors, in the case of quantum Rayleigh spontaneous emission additional correlations can be defined between different states of polarization – possibly boosting the detection counts – for two different angles φ1 and φ2 , relative to the x – axis of reference. Correlation functions Ec for a quantum behaviour are defined [16] as the expectation value of the tensor product of two measurement operators for a set of initial state vectors
E c = ⟨ Ψ ( φ1 ) │ ( θ1 ) ⊗ (
( θ1 ) ⊗ ( ( θ2 )│ Ψ (φ2 ) ⟩ = ⟨ Φ 1 │⊗│ Φ 2 ⟩ (1)
( θ2 )│ Ψ (φ2 ) ⟩ = ⟨ Φ 1 │⊗│ Φ 2 ⟩ (1)
where the initial state vector of spontaneous emission │Ψ (φ j )⟩ = cos φ j │ x ⟩ + sin φ j│ y ⟩ of Eq. (A3) of the Appendix below, is modified by the measurement operators , j = 1, 2 so that, │ Φ j ⟩ =  ( θj )│ Ψ (φ j )⟩ . This notation is equivalent to the definition of the correlation functions for a quantum behaviour [16] (Eq.13) of measurements performed at two different locations for pure states and φ1 = φ2. The polarization eigenstates of the measured photons, rotated by an angle θ j from the reference or generic states │ x ⟩ and │ y ⟩ are denoted as │ x ( θ j ) ⟩ = cos θ j │ x ⟩ + + sin θ j │ y ⟩ and │ y ( θ j ) ⟩ = - sin θ j | x ⟩ + cos θ j │ y ⟩ and the quantum operator measuring polarization properties of the photons is the projector
( θj )│ Ψ (φ j )⟩ . This notation is equivalent to the definition of the correlation functions for a quantum behaviour [16] (Eq.13) of measurements performed at two different locations for pure states and φ1 = φ2. The polarization eigenstates of the measured photons, rotated by an angle θ j from the reference or generic states │ x ⟩ and │ y ⟩ are denoted as │ x ( θ j ) ⟩ = cos θ j │ x ⟩ + + sin θ j │ y ⟩ and │ y ( θ j ) ⟩ = - sin θ j | x ⟩ + cos θ j │ y ⟩ and the quantum operator measuring polarization properties of the photons is the projector
 ( θj ) = │ x (θ j ) ⟩ ⟨ x (θ j ) │ - │ y (θ j ) ⟩ ⟨ y (θ j ) │ = sin (2 θ j )
( θj ) = │ x (θ j ) ⟩ ⟨ x (θ j ) │ - │ y (θ j ) ⟩ ⟨ y (θ j ) │ = sin (2 θ j )  1 + cos (2 θ j )
1 + cos (2 θ j ) 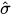 3 (2)
3 (2)
where  1 = │ x ⟩ ⟨ y │ + │ y ⟩ ⟨ x │ is the real part of the two-dimensional Pauli transition operator, flipping the photon between the two generic eigenstates, and
1 = │ x ⟩ ⟨ y │ + │ y ⟩ ⟨ x │ is the real part of the two-dimensional Pauli transition operator, flipping the photon between the two generic eigenstates, and  3 = │ x ⟩ ⟨ x │ - │ y ⟩ ⟨ y │ corresponds to the Pauli projection operator for the difference between the generic eigenstates. Using the identities of the operators:
3 = │ x ⟩ ⟨ x │ - │ y ⟩ ⟨ y │ corresponds to the Pauli projection operator for the difference between the generic eigenstates. Using the identities of the operators:  1 │ x ⟩ = │ y ⟩ ;
1 │ x ⟩ = │ y ⟩ ;  1 │ y ⟩ = │ x ⟩ ;
1 │ y ⟩ = │ x ⟩ ;  3 │ x ⟩ = │ x ⟩ ;
3 │ x ⟩ = │ x ⟩ ;  3 │ y ⟩ = - │ y ⟩ , and
3 │ y ⟩ = - │ y ⟩ , and  1
1  3 = -
3 = -  3
3  1 and
1 and  1
1  1 =
1 =  3
3  3 =
3 = 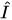 = │ x ⟩ ⟨ x│ + │ y ⟩ ⟨ y │ we obtain from Eq. (2) for the correlation operator:
= │ x ⟩ ⟨ x│ + │ y ⟩ ⟨ y │ we obtain from Eq. (2) for the correlation operator:
 ( θ1 ) ⊗ (
( θ1 ) ⊗ ( ( θ2 ) = cos 2 ( θ 1 - θ 2 )
( θ2 ) = cos 2 ( θ 1 - θ 2 ) 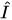 + sin 2 (θ 1 - θ 2 )
+ sin 2 (θ 1 - θ 2 )  1
1  3 (3)
3 (3)
By inserting Eqs. (3) and (A3), along with the equalities ⟨ Ψ ( φ1 ) │ Ψ ( φ2 ) ⟩ = cos (φ 1 - φ2) and ⟨ Ψ (φ1 )│  1
1  3 │Ψ (φ 2 )⟩ = = ⟨ Ψ (φ 1)│ Ψ ( φ 2 + π /2)⟩ = cos (φ1 - φ2 - π /2)) = sin (φ 1 - φ2 ) into Eq. (1), we evaluate the correlation function E c to be:
3 │Ψ (φ 2 )⟩ = = ⟨ Ψ (φ 1)│ Ψ ( φ 2 + π /2)⟩ = cos (φ1 - φ2 - π /2)) = sin (φ 1 - φ2 ) into Eq. (1), we evaluate the correlation function E c to be:
E c = cos 2 (θ 1 - θ 2) cos (φ 1 - φ2) + sin 2 (θ 1 - θ 2 ) sin (φ 1 - φ2) or
E c = cos [ 2 (θ 1 - θ 2 ) - (φ 1 - φ2 ) ] (4)
For φ 1 = φ 2 , this expression of the correlation function for single and independent qubits of the same state of polarization reaching both detectors, is identical to the expression for photonic entangled Bell states [17][18][19][20] (Ch.19), reaching the two detectors. Equally, Eq. (4) evaluates the correlation for the orthogonal detections, i.e., θ 1 - θ 2 = π / 2, of two different states of photon polarizations. With adjustable settings of the detecting polarization filters, i.e. θ 1 and θ 2 , any values of the correlation functions can be obtained [2][3][4] for corresponding values of the incoming photon polarization angles , i. e. , φ 1 and φ2.
The detection of photons having a polarization direction e k µ which is not aligned with the polarization filter e f will occur due to the probability of a dipole excitation being proportional to the scalar product e f • e k µ [11][12][13]. For photons to propagate in the same forward direction in a uniaxial crystal they need to be recaptured after spontaneous emission by the electric dipoles which are aligned with the principal axes of the crystal.
For initially identical states of photon polarization, that is φ 1 = φ 2 , a relation can be derived between the correlation function of the measurements Ec (θ 1, θ 2 ) = cos 2 ( θ 1 - θ 2 ) and the projection between the states of the detection filters, i. e., P (θ 1 , θ 2) =│⟨ Ψ (θ 1)│Ψ (θ 2) ⟩│2 = cos 2 (θ 1 - θ 2) . As in [17] (Ch.19), this relation is Ec (θ 1, θ 2 ) = 2 P (θ 1, θ 2 ) - 1 indicating that entangled states of photons do not possess any particular properties regarding quantum correlations associated with detections at two remote locations.
2.2 Mixed states of polarization
The overall correlation for one step of spontaneous emission will be found by adding up probability-weighted correlation functions of Eq. (4) as the ensemble of polarizations states generated over a time interval corresponds to a mixed quantum state described by the density matrix elements ρ m n (φ) = p (φ) ⟨ m │Ψ (φ) ⟩ ⟨ Ψ (φ) │ n ⟩ , where m, n = = x , y. A possible probability density can be identified from Eq. (A2) of the Appendix below, that is, p (φ) = (cos φ) 2 / (0.5 π), for generating the state│Ψ ( φ ) ⟩ over the range φ ∊ {–π/2, π/2}. This leads to a higher probability for the interval {–π/4, π/4} than for the intervals {– π/2, – π/4} and {π/4, π/2}.
The correlation function for the mixed state of an ensemble is evaluated similarly to Eq. (1) after using the transformation │Ψ ( φ ) ⟩ → p (φ)] 1/2 │Ψ ( φ ) ⟩ to obtain:
E c = cos [ 2 (u 1 - u 2) ] + ∫ d φ 2 √ p (φ 2 ) -π /2 ∫ π /2 √ p (φ 1 ) cos [ 2 (θ 1 - θ 2) - (φ 1 - φ 2 ) ] [ 1 – δ (φ 1 - φ 2 )] d φ 1 (5)
where the first term reproduces the result for identical and independent qubits, i.e., φ 1 = φ 2 , with δ being Dirac’s delta function, and the second term depends on the polarization state distribution of the mixed state, providing the possibility of controlling the level of correlation with various distributions of polarizations.
As the expectation values of the operator products of Eq. (3) are found to vanish for identical pure states of Eq. (A3), │ Ψ ( φ ) ⟩ = cos φ │ x ⟩ + sin φ │ y ⟩, namely ⟨ Ψ (φ ) │ 1
1  3 │ Ψ (φ) ⟩ = 0 and ⟨ Ψ (φ ) │
3 │ Ψ (φ) ⟩ = 0 and ⟨ Ψ (φ ) │ 3
3  1 │ Ψ (φ ) ⟩ = 0 , because
1 │ Ψ (φ ) ⟩ = 0 , because  1
1  3 │Ψ ( φ )⟩ = │ Ψ ( φ + π /2)⟩ , each term of the resulting commutative relation vanishes and we obtain:
3 │Ψ ( φ )⟩ = │ Ψ ( φ + π /2)⟩ , each term of the resulting commutative relation vanishes and we obtain:
⟨ Ψ (φ ) │[ 1 ,
1 ,  3 ]│ Ψ (φ ) ⟩ = 0 (6)
3 ]│ Ψ (φ ) ⟩ = 0 (6)
The eigenstates of  1 are superpositions of the eigenvectors of
1 are superpositions of the eigenvectors of  3 on the two-dimensional Hilbert space ℋ and simultaneous measurements of well-defined values are possible as their product operator
3 on the two-dimensional Hilbert space ℋ and simultaneous measurements of well-defined values are possible as their product operator  1
1  3 flips the eigenstates │ Ψ (φ ) ⟩ and │ Ψ (φ + π /2) ⟩ onto each other. Thus, the output value is indicative of the input one, and each term of the commutator vanishes for the wave functions │ Ψ (φ ) ⟩ of Eq .(A3). Consequently, the simultaneous measurement of the two operators in the context of the single and independent qubit wave functions is capable of identifying the incoming state as well as the measured one.
3 flips the eigenstates │ Ψ (φ ) ⟩ and │ Ψ (φ + π /2) ⟩ onto each other. Thus, the output value is indicative of the input one, and each term of the commutator vanishes for the wave functions │ Ψ (φ ) ⟩ of Eq .(A3). Consequently, the simultaneous measurement of the two operators in the context of the single and independent qubit wave functions is capable of identifying the incoming state as well as the measured one.
3. Physical aspects of simultaneous measurements of independent photons
Since the same correlation functions are derived for independent and single qubits generated through quantum Rayleigh conversion of photons - from initially entangled polarized photons - as for the initially entangled photons, it follows that the violations of any type of relevant Bell inequalities will also take place in the same way. Yet, the correlations result from similar, if not identical, distributions of polarization states as opposed to what is conceptually believed to be a non-local quantum effect which has an unspecified nature but is being pursued because of vested interests.
Once the same correlation functions are derived using only states of polarizations emitted spontaneously by the quantum Rayleigh conversion of photons, no other physical processes is required to explain the experimental results.
Let us now consider a few characteristics associated with local realism [6] of quantum measurements in the context of quantum Rayleigh conversion of photons:
Locality of measurements is supported by the use of single and independent photonic qubits emitted separately to explain the experimental results of apparently enhanced correlations of outcomes.
Randomness of experimental parameters stems from the quantum Rayleigh spontaneous emission that generates the projection from the polarization state │ x ⟩ of the input photons to the rotated polarization state │ Ψ (φ )⟩ = cos φ │ x ⟩ + sin φ │ y ⟩.
Realism of values carried by the detected photons is indicated by the physical effect of the measuring operators on the detected photons in quantum states │ Ψ (φ j ) ⟩ of Eq. (A3) for which the two commutator terms of the two Pauli operators of Eqs. (6) vanish independently of each other. Thus, a physically meaningful identification of wavefunctions will enable simultaneous measurements of well-defined values.
The common view [7] holds that “the measurement of one component of the entangled state collapses the total wave function into a certain value which, in turn, affects instantaneously the second measured value.” Nonlocality is associated with the instantaneous collapse of the wave function. The “remarkable” correlation is revealed by a comparison of the two lists of measured data compiled at the two detection points as ethereal influences are said to be associated with the collapse of the wave function upon measurement. Yet, the experimental results can be explained without entangled states of photons which are destroyed by propagating through a dielectric medium and replaced by independent qubits of photon polarization.
The presentation of [17] (Ch.19) describes the Einstein, Podolsky and Rosen (EPR) view suggesting that there is no such thing as an uncaused random event, and the characteristic randomness of the quantum world originates at the very beginning of each macroscopic event. By contrast, the conventional view [1] would have a quantum description in which the state vector evolves in a perfectly deterministic way from its initial value, and randomness enters only at the time of measurements. The quantum Rayleigh spontaneous emission is, in fact, a random process at the generating stage followed by evolution described by the Schrödinger equation, thereby supporting the EPR view.
It is emphasized in [5] that “Bell violation has less to do with quantum theory than previously thought, but everything to do with entanglement.” Actually, there is no need for entangled states to measure strong correlations of polarization between spontaneously emitted photons detected far apart from each other or non-locally.
It is claimed in [16] that “… the violation of Bell inequalities can be seen as a detector of entanglement that is robust to any experimental imperfection: as long as a violation is observed, we have the guarantee, independently of any implementation details, that the two systems are entangled.” Yet, this is not the case with single and independent qubits which can reproduce the same results.
For the entangled state of two polarized photons shown in the inset of [1] (Fig. 1), quantum mechanics predicts that the polarization measurements performed at the two distant stations will be strongly correlated [1]. But the same prediction also applies to two independent, single qubits which are generated through quantum Rayleigh spontaneous emission from initially identical photons propagating in different directions through dielectric media such as optical fibers.
Additionally, reference [18] “…rules out outcome-dependent causal models without additional assumptions in any scenario with more than two settings. A direct causal influence from one outcome to the other can therefore not explain quantum correlations.”
The analysis presented in this article is based on physically meaningful interactions of quantum Rayleigh conversion of photons and supports reference [6] in its statement that “There is no mystery. There is no quantum nonlocality”. It is the physical process that gives rise to a wave function. The opposite approach of relying on mathematical complexities to conjure up physical processes is bound to generate “‘quantum mysteries”.
As for the quantum key distribution between the two measuring units [19], it is determined by the local distribution of the mixed state of spontaneously emitted photons and the measurement setup of the dielectric devices involved in the polarization filtering with its eigenstates capturing the projected single qubits. However, errors will appear because of the statistical nature of the correlations between polarized photons.
The physical approach presented in this article can also explain the experimental results of reference [5] by invoking the quantum Rayleigh conversion of photons - see Appendix A below. This contrasts with the opinion article of reference [20] which dismisses the results of [5] as being irrelevant to the question of whether or not the quantum nonlocality is feasible.
4. Conclusions
Quantum Rayleigh conversions of photons in dielectric media provide a physically meaningful explanation for experimental results of statistical and “nonlocal” quantum correlations supposedly associated with entangled states of photons. Single and independent qubits replace the annihilated entangled states and provide identical correlation functions between two sets of polarization-related measurements carried out far apart from each other. This physically meaningful analysis raises significant doubts about the existence of photonics-based quantum nonlocality processes.
Appendix A- Spontaneous emission and polarization rotation induced by quantum Rayleigh conversion of photons
The probability of emitting a photon with momentum k and polarization µ is related to the decay rate γ s [1/s] of the excited dipole inside a dielectric medium, and evaluated as [14]:
γ sp ( k , μ, ω ) = [9 ε 5/2 / (2 ε + 1)] [2 π ω 3 / ( h c ) ] [ d ⋅ e k μ / 4 π] 2 (A1)
with d denoting the electric dipole moment vector which is excited by an optical field of the same polarization, e k µ being the polarization unit vector of the emitted photon, and which is perpendicular to the direction of propagation k . In a dielectric material of constant ε the decay rate is modified, but its angular distribution is the same as in free space.
The angular distribution of an accumulated number of spontaneously emitted photons N s p (D z, φ e m ) over a distance D z is found from Eq. (1), leading to:
N s p ( Δ z, φ e m ) = N s p (Δ z ) ( cos φ e m ) 2 (A2)
with φ e m the emission angle between the dipole d and the polarization unit vector e k µ of the photons and N s p (D z ) is calculated as in reference [11]. Spontaneously emitted photons with ± φ e m polarization angles relative to the pump polarization ep , will be amplified through the optically linear parametric gain coefficient [11][12][13] which will include a polarization dependence in the factor e p • e k µ , bringing about a correlation between the state of polarization and its number of amplified photons as found in [5].
For e k µ • x = cos φ e m and x • y = 0 , a non-vanishing value along the y –polarization is obtained by blocking off either + φ or - φ polarized photons as, for a large number of photons, the y –polarized photons cancel each other out. This corresponds to the use of a polarization filter for the polarization paradox which “rotates” photons from x to y.
The generic eigenstates of polarization associated with spontaneous emission through quantum Rayleigh conversion of photons on the two-dimensional Hilbert space ℋ will take the form of single and independent qubits │ Ψ ( φ e m ) ⟩ identified as:
│ Ψ ( φ e m ) ⟩ = cos φ e m │ x ⟩ + sin φ e m │ y ⟩ (A3)
These state vectors with polarization angles φ e m in the range -π / 2 ≤ φ e m ≤ π /2 will describe any possible polarization perpendicular to the direction of propagation of the spontaneous emission. Thus, incoming photons initially polarized in the x –direction will reappear with an angle θ – rotated polarization, thereby enabling them to pass through a θ – rotated polarization analyzer.
References
- A. Aspect, “Closing the Door on Einstein and Bohr’s Quantum Debate,” Physics 8, 123 ( 2015).
- B. Hensen, H. Bernien, A. E. Dréau, A. Reiserer, N. Kalb, M. S. Blok, J. Ruitenberg, R. F. L. Vermeulen, R. N. Schouten, C. Abellán, W. Amaya, V. Pruneri, M. W. Mitchell, M. Markham, D. J. Twitchen, D. Elkouss, S. Wehner, T. H. Taminiau, and R. Hanson, ‘‘Loophole-free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres,’’ Nature 526, 682-686 (2015).
- M. Giustina, M. A. M. Versteegh, S. Wengerowsky, J. Handsteiner, A. Hochrainer, K. Phelan, F. Steinlechner, J. Kofler, J.-Å. Larsson, C. Abellán, W. Amaya, V. Pruneri, M. W. Mitchell, J. Beyer, T. Gerrits, A. E. Lita, L. K. Shalm, S. W. Nam, T. Scheidl, R. Ursin, B. Wittmann, and A. Zeilinger, ‘‘Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons,’’ Phys. Rev. Lett. 115, 250401 (2015).
- L. K. Shalm, E. Meyer-Scott, B. G. Christensen, P. Bierhorst, M. A. Wayne, M. J. Stevens,T. Gerrits, S. Glancy, D. R. Hamel, M. S. Allman, K. J. Coakley, S. D. Dyer, C. Hodge, A. E. Lita, V. B. Verma, C. Lambrocco, E. Tortorici, A. L. Migdall, Y. Zhang, D. R. Kumor, W. H. Farr, F. Marsili, M. D. Shaw, J. A. Stern, C. Abellán, W. Amaya, V. Pruneri, T. Jennewein, M. W. Mitchell, P. G. Kwiat, J. C. Bienfang, R. P. Mirin, E. Knill, and S. W. Nam, ‘‘Strong Loophole-Free Test of Local Realism,’’ Phys. Rev. Lett. 115, 250402 (2015).
- X.-F. Qian, B. Little, J. C. Howell, and J. H. Eberly, “Shifting the quantum-classical boundary: theory and experiment for statistically classical optical fields,” Optica 2, 611-615 (2015).
- F. J. Tipler, Quantum nonlocality does not exist, PNAS, 2014, 111 (31), 11281-11286, August 5, 2014; https://doi.org/10.1073/pnas.1324238111.
- J. D. Griffiths, Introduction to Quantum Mechanics, Publisher: Pearson Prentice Hall, 2005.
- Recent reviewer reports provided by MDPI Photonics display unethical conduct on the part of reviewers with unspecified demands for improvements, or outright distortion of previous articles which apply the physical process of quantum Rayleigh conversion of photons. Reports provided by Optics Letters deny the existence of quantum Rayleigh scattering.
- W. H. Louisell, Quantum Statistical Properties of Radiation, John Wiley & Sons. , 1973.
- D. Marcuse, Principles of Quantum Electronics, Academic Press, 1980.
- Vatarescu, “Photonic coupling between quadrature states of light in a homogeneous and optically linear dielectric medium,” J. Opt. Soc. Am. B, 31, 1741–1745, 2014.
- A. Vatarescu, “Phase-Sensitive Amplification with Low Pump Power for Integrated Photonics,“ OSA Advanced Photonics Congress, paper ID: IM3A.6., 2016. A. Vatarescu,” Instantaneous Quantum Description of Photonic Wavefronts for Phase-Sensitive Amplification, “ Frontiers in Optics/Laser Science Conference (FiO/LS), paper JW4A.109, Washington, Sept. 2018.
- A. Vatarescu, “Photonic Quantum Noise Reduction with Low-Pump Parametric Amplifiers for Photonic Integrated Circuits”, Photonics 3, 61, 2016.
- R. J. Glauber and M. Lewenstein, Quantum optics of dielectric media, Phys. Rev. A, 43, 467- 491, 1991.
- Z. Wang, H. Wu, X. Hu, N. Zhao, Qi Mo and & G. Li, “Rayleigh scattering in few-mode optical fibers,” Sci. Rep. 6, 35844; doi:10.1038/srep35844 (2016).
- N. Brunner, D. Cavalcanti, S. Pironio, V. Scarani, and S. Wehner, ” Bell nonlocality,” Rev. Mod. Phys. 86, 419–478 (2014).
- J. C. Garrison and R.Y. Chiao, Quantum Optics, Oxford University Press, 2008.
- M. Ringbauer, C. Giarmatzi, R. Chaves, F. Costa, A. G. White and A. Fedrizzi, ”Experimental test of nonlocal causality”, Science Advances, 2 (8), 10 Aug 2016, DOI: 10.1126/sciadv.1600162.
- R. Ursin, F. Tiefenbacher, T. Schmitt-Manderbach, H. Weier, T. Scheidl, M. Lindenthal, B. Blauensteiner, T. Jennewein, J. Perdigues, P. Trojek, B. Ömer, M. Fürst, M. Meyenburg, J. Rarity, Z. Sodnik, C. Barbieri, H. Weinfurter, and A. Zeilinger, “ Entanglement-based quantum communication over 144 km,“ Nat. Phys., 3, 481–486 (2007).
- E. Karimi and R. W. Boyd “Classical entanglement? “ Science Magazine, 350 (6265), 1172-1173, Dec. 2015.




