The Influence of Exogenous Factors

Exogenous factors can affect the production process by either changing the (X, Y) configuration on the attainable set, shifting the efficient boundary, or by affecting the distribution of inefficiencies, and the probability for the unit under evaluation to reach its optimal input/output ratio. It is possible that both effects are present or completely independent of the production process. Alda ^[1] provide an interesting perspective on this. The authors, based on postulates of the contingency theory, argue that because of the public nature of police organizations’ activities, they are heavily influenced by the environmental factors which invariably affect their efficiency.

Some procedures to consider the role of external factors have been proposed. Most of them are based on two or multiple stages and regression inferences, which, as discussed by Simar & Wilson ^{[2] [3]} and Daraio & Simar ^[4] are flawed by the development of biased estimators of the efficiency scores, serially correlated estimates and by the necessity to impose parametric assumptions on the production process. For a state-of-the-art literature review on the inclusion of environmental variables in nonparametric frontier models, see ^[5].

The Model Explained

Conditional efficiency measures, accounting for environmental uncontrollable factors (Z), were introduced by Daraio & Simar (2005)^[6]. They are based on the basic idea that the joint probability distribution  when conditional on Z = z can define an attainable production set such that x can produce y if Z = z ^[7].

The advances in Nonparametric Robust Estimators [16–18], besides the benefit of not imposing a functional specification for the frontier projection, are also not affected by extremes production observations and outliers data. This is due to the projection of partial frontiers of order-m or order-α which do not envelop all data points, being less affected to extreme data values [17]. In this particular application, a directional version of the FDH is provided, which results are robust to outliers and extreme values.

Conditional Frontier Analysis ^[6][8] in its directional version ^[9] is part of the Nonparametric Robust Estimators proposed to overcome some drawbacks in the traditional DEA measures for the technical efficiency. The application of this methodology permits an assessment of police performance by considering criminal data as exogenous variables (Z) that are not under the service units' control. Consider a particular DMU j from a set of m decision units using i = 1, 2, 3 …, n inputs to produce r = 1, 2, 3 …, s outputs. The directional efficiency is obtained by choosing a feasible direction g_(x,y) ≥ 0 for contracting resources (inputs) and/or expanding results (outputs) to reach the industry efficient frontier:         

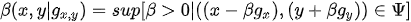
(1)

The results for efficiency projections depend on the choice of the directional input vectors, aiming to contract the production resources and choose the directional output vectors, aiming to expand the products. Thus, the overall evaluation is sensitive to the opted directions. From an economic point of view, this is consistent with the optimization behavior of service units (maximizing results or reducing production costs). Nepomuceno et al. ^[10] offer a brief discussion on the choice of sustainable directions, and a review of methodologies for selecting directions in a non-parametric framework can be found in the work of Wang et al. ^[11]. For instance, directions can be defined exogenously, including subjective preferences or conditional techniques or they can be defined endogenously by optimization approaches. While the former has the benefit of flexibility for decision-making, the latter has the adherence of statistical properties and theoretical support.

The choice for the data direction g(x,y) = (X,Y) or for the unit vector g(x,y) = (1, 1) are the most appropriate in many circumstances due to the simplicity of underlying aggregations. In this assessment, we opt for the unit vector. Because this assessment can be considered a two-step methodology (first an efficiency application, then prioritization), choosing another potential flexible or optimized direction would require double aggregations, and the results in the prioritization phase (for constructing the effective-efficient sub-ranks) would be biased. Exogenous factors can affect police production by changing the input/output configuration or by affecting the distribution of inefficiencies. Including potential exogenous determinants of efficiency is based on the premise that the joint probability distribution H(XY) = prob (X ≤ x, Y ≥ y) when conditional to Z = z can define an attainable production such that x can produce y when Z = z. For the directional efficiency, the conditional directional distance function is defined as [35,36]:

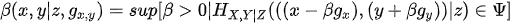
(2)

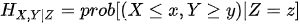is the joint conditional probability that a given unit j with production (X, Y) dominates the unit under evaluation with production configuration (x, y). This is empirically developed using a non-parametric estimator that smooths the multiple exogenous factors Z in the neighborhood of z from a sample q = 1, 2, 3, …, p observations based on an appropriate kernel estimation and choice for a bandwidth vector.

The joint conditional probability measure prob(X <= x,Y >= y)|Z=z  is empirically estimated by a non-parametric estimator that smooths the multiple  values in the neighborhood of z from a sample  of  observations:

(3)

In the work of Nepomuceno et al.^{[12] [8]} the application of this methodology was made on three models developed to derive FDH directional efficiency measures which compose the decision criteria in the ranking of municipalities: a model for Violent Crimes clear-ups as output (CVLI – Crimes Violentos Letais e Intencionais), a model for Street Mugging as output (Trans - Assalto a Transeúnte) and the last one for Carjacking as output (Veíc - Roubo de Veículos), all conditional to the occurrences, using sworn and administrative officers as input.

This entry is from 10.3390/su13084251 and from 10.1007/s10479-020-03767-6