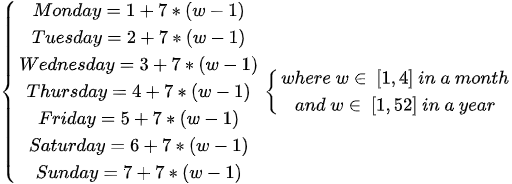| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Claude El-Bayeh | + 1451 word(s) | 1451 | 2020-05-23 15:57:46 | | | |
| 2 | Claude El-Bayeh | + 1447 word(s) | 1447 | 2020-05-25 05:10:52 | | | | |
| 3 | Claude El-Bayeh | -4 word(s) | 1443 | 2020-05-26 21:33:41 | | | | |
| 4 | Lily Guo | -66 word(s) | 1377 | 2020-10-28 07:52:39 | | | | |
| 5 | Lily Guo | Meta information modification | 1377 | 2020-10-28 07:54:08 | | | | |
| 6 | Lily Guo | Meta information modification | 1377 | 2020-10-28 07:54:49 | | | | |
| 7 | Lily Guo | Meta information modification | 1377 | 2020-10-28 07:55:15 | | | | |
| 8 | Rita Xu | Meta information modification | 1377 | 2022-11-15 09:20:16 | | | | |
| 9 | mamang kuy | + 29 word(s) | 1406 | 2022-12-01 11:03:54 | | | | |
| 10 | Peter Tang | -29 word(s) | 1377 | 2023-01-12 03:57:05 | | |
Video Upload Options
Has anyone of us missed an event because he was confused between days and dates? Do we really remember the date of any day if we do not have a calendar? Is the current Gregorian Calendar efficient enough for use, and does it really facilitate our life or make it more complicated? Have you ever thought about a much simpler way to calculate days and dates in a year? All these questions are answered in this article, in which the author proposes an original calendar that might facilitate our lives if we can apply it.
1. Introduction
In modern times, most of the countries in the world use “Gregorian calendar” in their daily life, and every event, holiday are based on this calendar system[1][2]. It is introduced in October 1582 by Pope Gregory XIII. In the Gregorian Calendar, a year is composed of 12 months. Each month has a different number of days. For example, January has 31 days, February has 28 days, and sometimes 29, April has 30 days, and so on. Sometimes, the dates become confusing especially when a particular day like Monday, is the first day in a month, and the second or even the seventh in another month, sometimes holidays which are on a specific date such as 24 December, could be located during the weekdays (e.g., in 2019), while it can be in weekends in another year (e.g., 2022). It appears that the existing calendar system becomes a little bit confusing for most of us, and we need something much easier to handle and more practical to rely on.
What happens if we create a more organized Calendar in which the days and dates in a month do not change? For example, Monday will always be the first day of any month. The holidays will have the same dates and days in a year. For example, 24 December will always be on Wednesday every year and so on. Do we think that this method might be easier to memorize and to use? Moreover, humans always develop and invent new things every day to facilitate their lives. So why not developing an easier way to count days, weeks, and months in a year?
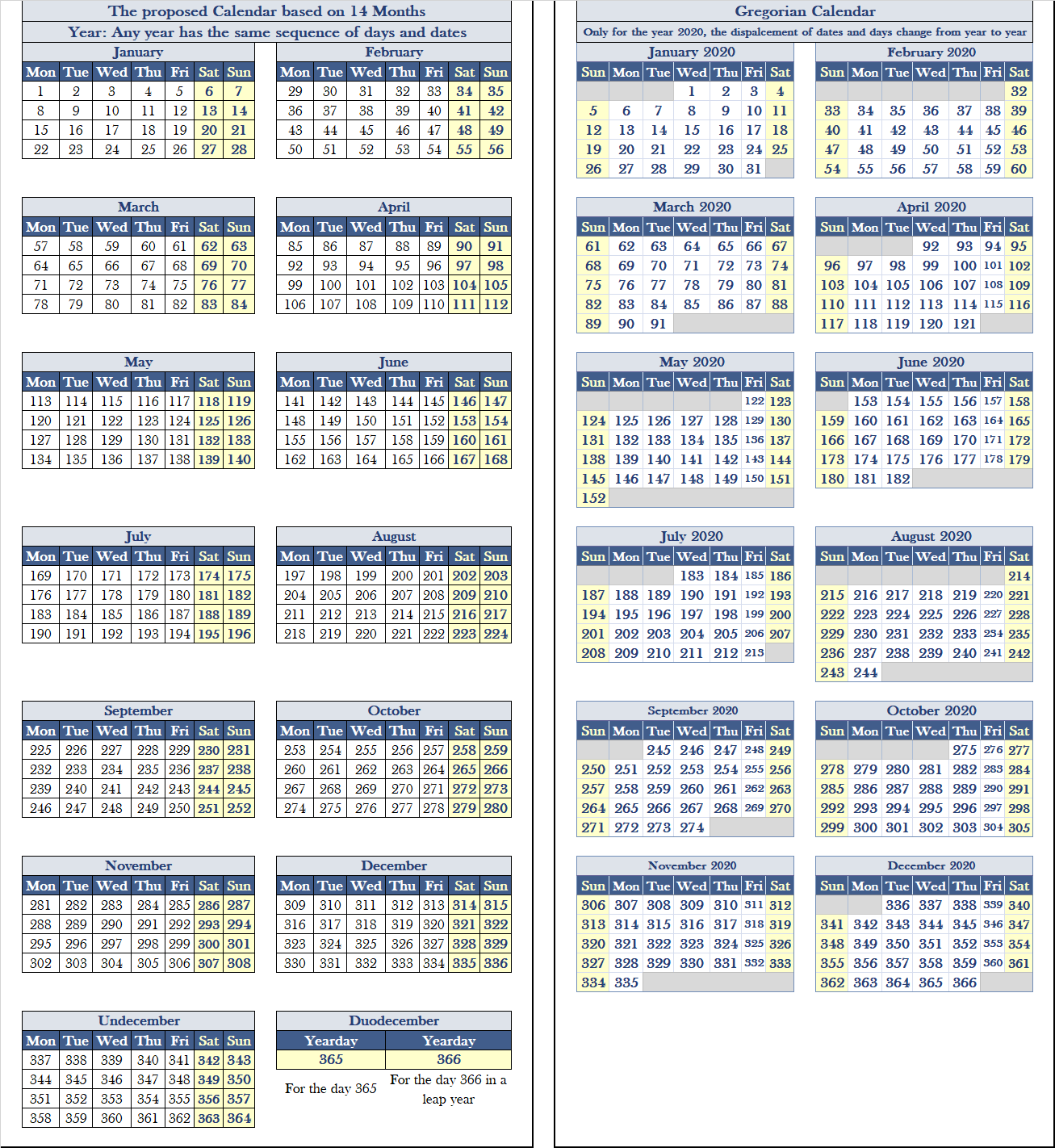
In this article, the author proposes a calendar year of 14 months instead of 12, in which each month of the first thirteen contains exactly 28 days. In total, we have 364 days for the first thirteen months. The remaining days (number 365, and 366 in a leap year) will be added to the fourteenth month. The advantages and disadvantages of the proposed Calendar are stated in this paper.
2. Materials Methods and Development
A year on earth has approximately 365.2425 days and 12 months according to the Gregorian Calendar. Each month has almost between 28 and 31 days. In the current Gregorian Calendar, a year has nearly 52.1428 weeks. A week always starts on a specific day (such as Monday). However, the date of the day is different from a year to another. For example, the first day in January 2020, is Wednesday, while it is Friday in 2021. Moreover, the first day of each month also changes. For instance, the first day in January 2020 is Wednesday, while it is Saturday in February 2020, and Sunday in March 2020. Christmas in 2020 is on Thursday 20, while it is on Friday 24 in 2021.
It becomes more complicated when a leap year is added every four years, and an additional day is added to the month of February, which becomes equal to 29 days instead of 28 every four years. In this article, we suggest a new calendar system weekly-based in which it has 14 months to minimize the complexity. In order to create such Calendar, we should follow the mentioned steps as below:
-
We start to define a week. A week has only 7 days, and it always starts on Monday.
-
The first 13 months have exactly 4 weeks, in which the total number of days becomes equal to 28 only (7 days x 4 weeks)
-
The first 13 months have precisely the same number of days, and they start exactly with the same day (Monday) and end with the same day (Sunday)
-
The number of days in the first 13 months cannot change even during a leap year. They are always fixed to 28 days per month, whatever is the year.
-
The number of weeks in a year is fixed to 52. In fact, the number of weeks should be 52.1428 (365 days / 7 days = 52.1428); however, we approximate it to 52 for simplicity
-
After doing all these calculations, the total number of days in a year becomes equal to 364 days per year (52 weeks per year x 7 days per week).
-
The remaining days of the year are named “Yeardays,” and they are added to the last month of the year (month number 14). Practically, the last month has only 1 or 2 days. This method will solve lots of problems. For example, day number 365 is called “Yearday 1”, which is the end of a year and it is not included in any month or week. For the case of a leap year, day number 366 is called “Yearday 2”, in this way the Calendar doesn’t change. An example is shown in the following tables.
|
Normal Year |
Next Year |
|||||||||
|
Day |
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
Saturday |
Sunday |
Yearday 1 |
Monday |
Tuesday |
|
number |
358 |
359 |
360 |
361 |
362 |
363 |
364 |
365 |
1 |
2 |
|
Leap Year |
Next year |
|||||||||
|
Day |
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
Saturday |
Sunday |
Yearday 1 |
Yearday 2 |
Monday |
|
number |
358 |
359 |
360 |
361 |
362 |
363 |
364 |
365 |
366 |
1 |
3. Results and Discussions
If we elaborate on all the above steps, we can create a new calendar year, which has the following form:
Figure 1: Proposed Calendar with 14 months in a year and 28 days in a month.
The number of days in a sequence in a calendar year will also have the following form:
Figure 2: Sequence numbering of days in the proposed Calendar.
The following Figures compare the Gregorian Calendar to the proposed one in this article.
Figure 3: Comparison between the proposed Calendar and the Gregorian Calendar for the year 2020.
Figure 4: Comparison between the sequence numbering of the days in a year for the proposed Calendar and the Gregorian Calendar for the year 2020.
From the above Figures, it is clear that the proposed Calendar in this paper has a more systematic organization of the days in a week, month, and year. The first day of a month always starts on Monday, and the last day of each month is always Sunday. Therefore, counting days becomes an easy task, and there is no need for complex algorithms to predict the days and dates in previous years.
The calculation of the date for a specific day is straightforward and can be done using the following proposed equations:
and
Where w is the week number in a month (w in [1,4]) or a year (w in [1,52]).
Example:
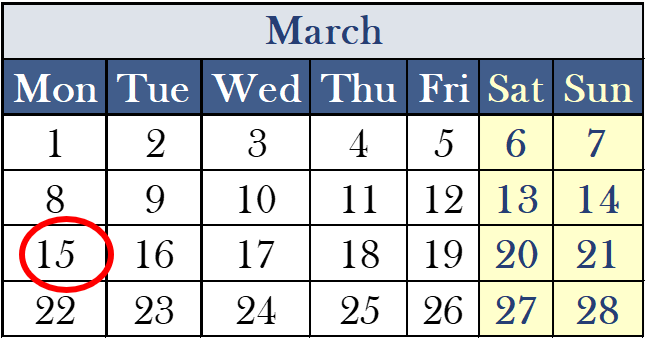
Calculate the date of the Monday in the third week of a month and check it on the Calendar to see if it is correct.
Answer:
Monday=1+7(w-1)=1+7(3-1)=15
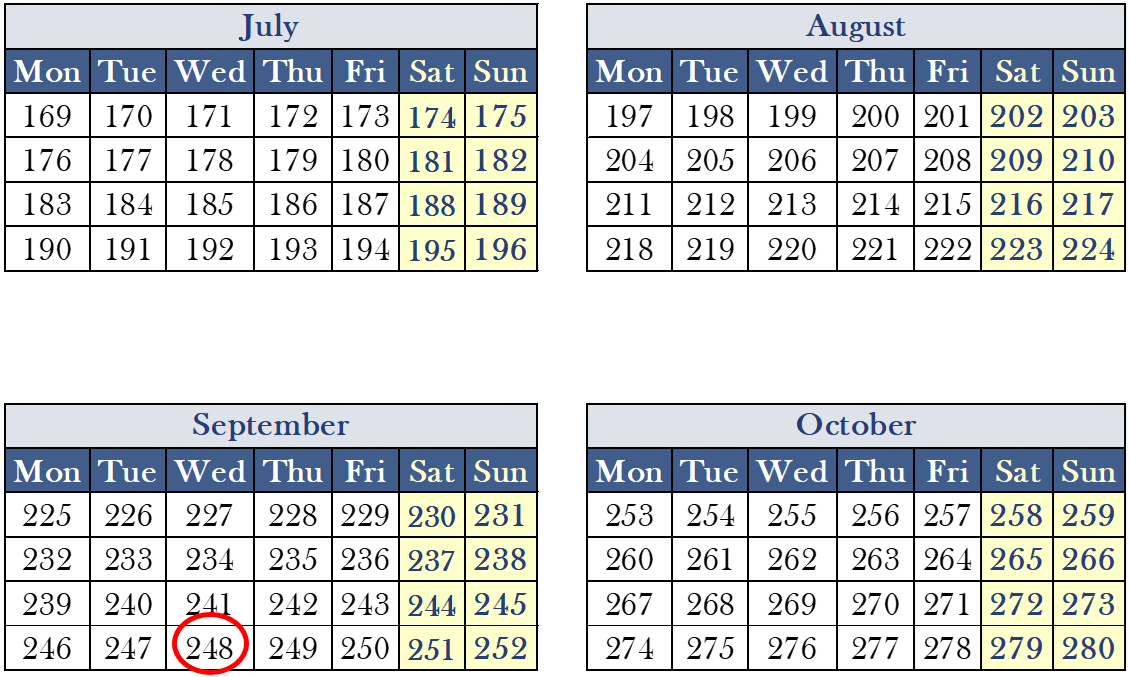
Example:
Calculate the day number of Wednesday located on the 36th week of the year, and check it on the Calendar to see if it is correct.
Answer:
Wednesday=3+7(w-1)=3+7(36-1)=248
To conclude the study, a comparative table between the proposed Calendar and the Gregorian Calendar shows the advantages and disadvantages of each system.
|
Description |
Proposed Calendar |
Gregorian Calendar |
|
Number of days in the weekends per year |
Up to 106 |
Up to 104 |
|
Number of payable months |
13 |
12 |
|
Complexity of the system |
easy |
Complex |
|
Computation time |
Very low |
Very high[3] |
|
Time wasted just to see the day and date on a calendar |
Very low |
Very high |
|
Do we really need a Calendar to check the dates |
No |
Yes |
In this entry, the author proposes an original calendar based on 14 months instead of 12. Each of the first thirteen months has exactly 28 days. The last month has only 1 or 2 days, and it is added in purpose to facilitate the calculation considering the standard (ISO 8601). The new Calendar is much easier to understand and calculate. We do not need complex algorithms to calculate the dates and days in a year. Moreover, the proposed Calendar fixes the days and their dates in a month and year. Therefore, the dates will be the same whatever is the year, contrary to the Gregorian Calendar. Are we able to apply this new Calendar in our daily life? Does it seem logical to try it and see what it can change in our life? The author asks the readers to share their comments and suggestions.[1][2][3]
References
- C. A. Ronan, "The Gregorian Calendar," The New Encyclopaedia Britannica, pp. 602-603.
- E. L. Cohen, "Adoption and reform of the Gregorian calendar," Math Horizons, vol. 7, no. 3, pp. 5-11, 2000.
- N. Dershowitz and E. M. Reingold, "Calendrical calculations," Software: Practice and Experience, vol. 20, no. 9, pp. 899-928, 1990.