| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Milan Toma | + 1569 word(s) | 1569 | 2021-04-07 08:31:33 | | | |
| 2 | Milan Toma | Meta information modification | 1569 | 2021-04-07 14:16:27 | | | | |
| 3 | Lily Guo | Meta information modification | 1569 | 2021-04-08 02:50:35 | | |
Video Upload Options
Smoothed-particle hydrodynamics is a computational mesh-free Lagrangian method developed by Gingold, Monaghan, and Lucy in 1977, initially intended for use in astrophysics.
1. Introduction
Smoothed-particle hydrodynamics is a computational mesh-free Lagrangian method developed by Gingold, Monaghan, and Lucy in 1977, initially intended for use in astrophysics [1][2]. Since then, it has been used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It has been used in many fields outside astrophysics, including ballistics, volcanology, and oceanography. In recent years, it has been increasingly adopted by those with an interest in biomedical engineering [3][4][5].
Succinctly speaking, a continuous field is reconstructed from a cloud of discrete particles. Each of the particles has assigned properties, i.e., mass, pressure, velocity, density (volume). The kernel function is used to encircle several other neighboring particles by the radius of the smoothing length (Figure 1). That means that any property can be reconstructed by taking the volumetric integral of the kernel function multiplied by the local value of a given property, e.g., the pressure, where
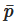
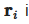
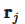
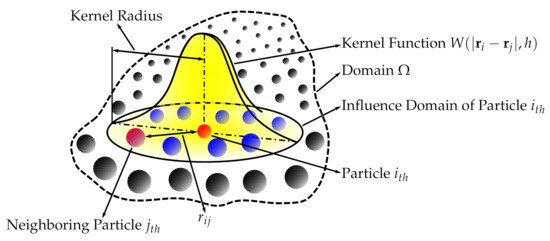
Figure 1. Smoothed-particle hydrodynamics with a kernel approximation.
The SPH is governed by a set of ordinary differential equations as follows. The continuity equation, i.e., conservation of mass, is
where W is the Kernel function and the 4th order diffusive term improves the pressure evolution.
The momentum equation, i.e., Euler equation, is
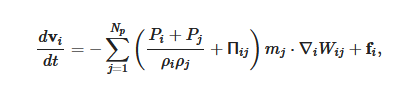
More detail on the numerical methods used in the cardiovascular FSI simulations, e.g., the integration method, artificial viscous term, laminar viscous term, speed of sound used, can be found published elsewhere [6][7].
The SPH interacts with the structural finite elements using a penalty-based contact algorithm. In penalty-based contact, when a penetration is found, a force proportional to the penetration depth is applied to resist and eliminate penetration. Linear contact spring stiffness is based on the nodal masses that come into contact and the time step size as follows
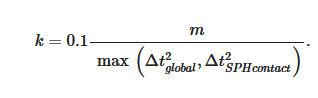
The resulting contact stiffness is independent of the material constants so it is well suited for treating contact between fluid and structure. Fluid–structure coupling is achieved by using a position-based Verlet time integration scheme that enforces momentum conservation. Solid particles are assigned a velocity and acceleration which are averaged over a fluid time step to enhance force matching [8].
The combination of the SPH method (used to simulate the fluid domain flow) with a high-order finite element method (used to simulate the solid domain deformations) is ideal for simulating FSI, especially when complex geometries are included. Using SPH methods provides numerical stability because the contact between the solid and fluid domains is easily treated numerically. Moreover, SPH is highly parallelizable. Hence, it is possible to run FSI simulations with geometries complex preserving all their details, and at the same time keeping the simulations numerically stable, accurate, parallelized on a standard GPU workstation (as opposed to large supercomputers), and all of that with a runtime of only hours or days rather than weeks and months.
2. Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics
Two notable implementations of SPH-FSI in biomedical applications, namely, blood flow and cerebrospinal fluid flow interactions, have been explored more than other applications. This section is divided accordingly.
2.1. Blood Flow in Arteries
The first time SPH was found to be used to replicate a three-dimensional FSI biomechanical process was in 2003, with the introduction of a three-dimensional thick-wall model using FSI to simulate blood flow in the carotid arteries with stenosis [9][10]. Previous mathematical models had been restricted to being one-dimensional and their accuracy was limited because only the average axial velocity and pressure over the cross-section of the tube were calculated [11]. Prior to 2003, higher dimensional models had been used to investigate FSIs in the collapse and ablation of atheromatous plaques in the coronary arteries [12]. They found that wall stress distribution had a very localized pattern and that the dragging force from fluid flow had a considerable effect on wall compression. Other studies formed the foundation for computations for fluid and wall motions in models of arterial stenosis and abdominal aneurysm [13][14]. Stress concentration, found at both edges of the stenosis, was concluded to be responsible for plaque ablation. FSI finite element analysis of pulsatile flow through compliant axisymmetric stenotic arteries was also done and findings showed that severe stenosis causes artery compression, negative flow pressure, and high flow shear stress [15].
More recently, this model has been adopted again, but for simulations of blood flow in patient-specific geometries utilizing CT technology [16][17][18][19]. Furthermore, the particle nature of the SPH method facilitates a convenient platform to model platelets, allowing models to simulate the process of thrombogenesis under the influence of various blood flow parameters [20]. As pointed out throughout this article, the use of SPH is especially justified when the geometries used are complex.
2.2. Blood Flow’s Interaction with Heart
In recent years, SPH has been used more commonly to simulate the closure of heart valves. Its purpose is to assess the efficacy of surgical procedures and medical devices. The complexity of heart valve geometries, combined with the large deformations they undergo with every heartbeat between their fully open and fully closed positions, make SPH ideal for conducting computational FSI analyses. The SPH method was demonstrated and validated in several articles on mitral valve closure [7][21][22][23]. Subsequently, it was used to assess several diseased mitral valve states [24][25][26][27] and applications of medical devices designed to correct them [28][29][30][31]. Besides the mitral valve, other valves have been studied using the same methods [23][32][33][34][35][36]. The SPH method has been validated to study the hemodynamics of the left ventricle [6]. Interaction between bioprosthetic heart valves and blood was also studied using SPH [37]. An overview of numerical methods, including SPH, for FSI models of aortic valves, can be found in [38].
2.3. Cerebrospinal Fluid’s Interaction with the Brain
The brain, with its intrinsic topology, is the most complex organ in the human body making computational models inherently challenging. The majority of computational models in the literature routinely embed it into lower dimensions. The particle nature of the SPH method allows for a more detailed analysis of the complex neurological structures while having the ability to simulate their interactions with surrounding cerebrospinal fluid.
FSI simulations using SPH are used to demonstrate and to study the cushioning effect of cerebrospinal fluid [39][40][41] and the mechanism of brain injuries induced by an outside loading factor [42][43][44][45]. In the context of disease diagnosis and management, these models are able to assess the risk of developing neurological complications, such as hemorrhage, following treatment in addition to explaining the possible pathophysiology behind the condition itself [46].
Furthermore, the use of SPH is shown to play a role in calculating potential ballistic pathways in forensic investigation. To inform the investigation process, the following are analyzed: the entry wound and blood spatter patterns, the influence of target materials, and the cranial geometry. Using SPH, we can develop a numerical model capable of simulating high-speed ballistic impacts, thus allowing for the standardized evaluation and simulation of “backspatter”, the retrograde ejection of blood and tissue from the entry wound following projectile impact, which can then help determine the proximity of the shooter and potentially differentiate between suicide and homicide [47].
2.4. Other Applications
While the SPH method has been more commonly used in heart and brain simulations, other applications have also been explored. As previously stated, the more complex the simulation, the more appropriate it is to use the SPH method. For example, the act of swallowing is a complex process involving soft tissue, muscle, and bone, all of which must be included in order to make the simulations accurate/practical [48][49]. As such, the simulation requires multiple parts whose relationships must be included in the calculation: the soft structures (i.e., pharyngeal wall, soft palate, and tongue) are simulated using a finite element method, bony structures (e.g., mandible, hard palate, and hyoid) are simulated as rigid bodies, and a fluid bolus is simulated using SPH. Mathematical and computational modeling of the stomach is another emerging field of biomechanics where several complex phenomena, such as gastric electrophysiology, fluid mechanics of the digesta, and solid mechanics of the gastric wall, need to be addressed. SPH is a promising approach to model multiphase flows specifically in the gastric lumen [50]. SPH has also been successfully applied in computational modeling of the small intestine [51].
Thus far, all biomedical applications mentioned above are applied to the inside of the human body. However, the interaction of the human body with outside fluid domains can also be considered. For example, an SPH model is used to predict the loading on the human body during elite platform diving [52]. Other studies in human movement science focus on the analysis of stroke technique and the interactions between the water, the paddle, and the kayak [53]. Though technically, that study does not involve direct interaction between the human body and fluid, it does fall under the umbrella of biomedical FSI applications. Furthermore, the body can also interact with, and be damaged by, outside solid objects. Studies looking to understand the anatomical changes that lead to femoral cortical bone remodeling in hip fractures and how such changes affect healing and functionality are one example [54]. As such, the investigation of impact biomechanics is of great interest in the understanding of damages caused by the impact of a projectile with the human body [55].
References
- Lucy, L. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024.
- Gingold, R.; Monaghan, J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389.
- Ye, T.; Pan, D.; Huang, C.; Liu, M. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 2019, 31, 011301.
- Zhang, L.; Ademiloye, A.; Liew, K. Meshfree and Particle Methods in Biomechanics: Prospects and Challenges. Arch. Comput. Methods Eng. 2019, 26, 1547–1576.
- Toma, M. The Emerging Use of SPH in Biomedical Applications. Signif. Bioeng. Biosci. 2017, 1, SBB.000502.
- Durrwachter, J. Hemodynamics of the Left Ventricle: Validation of a Smoothed—Particle Hydrodynamics Fluid-Structure Interaction Model. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2016.
- Toma, M.; Einstein, D.; Bloodworth, C.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid-Structure Interaction and Structural Analyses using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2815.
- Zhang, C.; Rezavand, M.; Hu, X. A Multi-Resolution SPH Method for Fluid-Structure Interactions. J. Comput. Phys. 2021, 429.
- Tang, D.; Yang, C.; Kobayashi, S.; Zheng, J.; Vito, R. Effect of stenosis asymmetry on blood flow and artery compression: A three-dimensional fluid-structure interaction model. Ann. Biomed. Eng. 2003, 31, 1182–1193.
- Tang, D.; Yang, C.; Kobayashi, S.; Ku, D. Steady flow and wall compression in stenotic arteries: A three-dimensional thick-wall model with fluid–wall interactions. J. Biomech. Eng. 2001, 123, 548–557.
- Downing, J.M.; Ku, D.N. Effects of Frictional Losses and Pulsatile Flow on the Collapse of Stenotic Arteries. J. Biomech. Eng. 1997, 119, 317–324.
- Yamaguchi, T.; Kobayashi, T.; Liu, H. Fluid-wall interactions in the collapse and ablation of an atheromatous plaque in coronary arteries. In Proceedings of the Third World Congress of Biomechanics, Sapporo, Japan, 2–8 August 1998; p. 20b.
- Yamaguchi, T.; Furuta, N.; Nakayama, T.; Kobayashi, T. Computations of the fluid and wall mechanical interactions in arterial diseases. In Proceedings of the 1995 ASME International Mechanical Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; pp. 197–198.
- Yamaguchi, T.; Nakayama, T.; Kobayashi, T. Computations of the wall mechanical response under unsteady flows in arterial diseases. Adv. Bioeng. 1996, 33, 369–370.
- Bathe, M.; Kamm, R. A fluid-structure interaction finite element analysis of pulsatile blood flow through a compliant stenotic artery. J. Biomech. Eng. 1999, 121, 361–369.
- Wong, K.; Fong, F.; Wang, D. Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modelling through CT reconstructed arteries. J.-Ray Sci. Technol. 2017, 25, 213–232.
- Nasar, A. Eulerian and Lagrangian Smoothed Particle Hydrodynamics as Models for the Interaction of Fluids and Flexible Structures in Biomedical Flows. Ph.D. Thesis, The University of Manchester (United Kingdom), PQDT-UK & Ireland, Manchester, UK, 2016.
- Yang, C.; Tang, D.; Atluri, S. Patient-specific carotid plaque progression simulation using 3D meshless generalized finite difference models with fluid–structure interactions based on serial in vivo MRI data. Comput. Model. Eng. Sci. 2011, 72, 53–77.
- Chui, Y.P.; Heng, P.A. A meshless rheological model for blood-vessel interaction in endovascular simulation. Prog. Biophys. Mol. Biol. 2010, 103, 252–261.
- Al-Saad, M.; Suarez, C.; Obeidat, A.; Bordas, S.; Kulasegaram, S. Application of Smooth Particle Hydrodynamics Method for Modelling Blood Flow with Thrombus Formation. Comput. Model. Eng. Sci. 2020, 122, 831–862.
- Toma, M.; Bloodworth, C.; Einstein, D.; Pierce, E.; Cochran, R.; Yoganathan, A.; Kunzelman, K. High-resolution subject-specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630.
- Toma, M.; Jensen, M.; Einstein, D.; Yoganathan, A.; Cochran, R.; Kunzelman, K. Fluid-Structure Interaction Analysis of Papillary Muscle Forces Using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Ann. Biomed. Eng. 2016, 44, 942–953.
- Mao, W.; Caballero, A.; Kodali, S.; Sun, W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729.
- Caballero, A.; Mao, W.; McKay, R.; Primiano, C.; Hashim, S.; Wei, S. New insights into mitral heart valve prolapse after chordae rupture through fluid—Structure interaction computational modeling. Sci. Rep. 2018, 8, 17306.
- Mao, W.; Caballero, A.; Hahn, R.; Sun, W. Comparative quantification of primary mitral regurgitation by computer modeling and simulated echocardiography. Am. J. Physiol. Heart Circ. Physiol. 2020, 318, H547–H557.
- Toma, M.; Bloodworth, C.; Pierce, E.; Einstein, D.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid-Structure Interaction Analysis of Ruptured Mitral Chordae Tendineae. Ann. Biomed. Eng. 2017, 45, 619–631.
- Biffi, B.; Gritti, M.; Grasso, A.; Milano, E.; Fontana, M.; Alkareef, H.; Davar, J.; Jeetley, P.; Whelan, C.; Anderson, S.; et al. A workflow for patient-specific fluid–structure interaction analysis of the mitral valve: A proof of concept on a mitral regurgitation case. Med. Eng. Phys. 2019, 74, 153–161.
- Toma, M.; Einstein, D.; Kohli, K.; Caroll, S.; Bloodworth, C.; Cochran, R.; Kunzelman, K.; Yoganathan, A. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology 2020, 9, 173.
- Toma, M.; Einstein, D.; Bloodworth, C.; Kohli, K.; Cochran, R.; Kunzelman, K.; Yoganathan, A. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-valvular Spacer. Prosthesis 2020, 2, 7.
- Caballero, A.; Mao, W.; McKay, R.; Hahn, R.; Sun, W. A Comprehensive Engineering Analysis of Left Heart Dynamics After MitraClip in a Functional Mitral Regurgitation Patient. Front. Physiol. 2020, 11, 432.
- Caballero, A.; Mao, W.; McKay, R.; Wei, S. Transapical mitral valve repair with neochordae implantation: FSI analysis of neochordae number and complexity of leaflet prolapse. Int. J. Numer. Methods Biomed. Eng. 2019, 36, e3297.
- Singh-Gryzbon, S.; Sadri, V.; Toma, M.; Pierce, E.; Wei, Z.; Yoganathan, A. Development of a Computational Method for Simulating Tricuspid Valve Dynamics. Ann. Biomed. Eng. 2019, 47, 1422–1434.
- Mao, W.; Li, K.; Sun, W. Fluid—Structure interaction study of transcatheter aortic valve dynamics using smoothed particle hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388.
- Caballero, A.; Mao, W.; McKay, R.; Wei, S. The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: A comprehensive computational analysis. J. R. Soc. Interface 2019, 16, 20190355.
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. The Impact of Self-Expandable Transcatheter Aortic Valve Replacement on Concomitant Functional Mitral Regurgitation: A Comprehensive Engineering Analysis. Struct. Heart 2020, 4, 179–191.
- Dabiri, Y.; Yao, Y.; Sack, K.; Kassab, G.; Guccione, J. Tricuspid valve regurgitation decreases after mitraclip implantation: Fluid structure interaction simulation. Mech. Res. Commun. 2019, 97, 96–100.
- Yuan, Q.; Ye, X. A New Way to Simulate the Fluid Structure Interaction between the Bioprosthetic Heart Valve and Blood: FE-SPH Method; Mechanical Science and Engineering IV; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 472, pp. 125–130.
- Marom, G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch. Comput. Methods Eng. 2015, 22, 595–620.
- Toma, M.; Nguyen, P. Fluid-structure interaction analysis of cerebrospinal fluid with a comprehensive head model subject to a rapid acceleration and deceleration. Brain Inj. 2018, 32, 1576–1584.
- Duckworth, H.; Ghajari, M. Modelling Brain Biomechanics Using a Hybrid Smoothed Particle Hydrodynamics and Finite Element Model; Ohio State University Injury Biomechanics Symposium: Columbus, OH, USA, 2019.
- Wilhelm, J.; Ptak, M.; Fernandes, F.; Kubicki, K.; Kwiatkowski, A.; Ratajczak, M.; Sawicki, M.; Szarek, D. Injury Biomechanics of a Child’s Head: Problems, Challenges and Possibilities with a New aHEAD Finite Element Model. Appl. Sci. 2020, 10, 4467.
- Toma, M.; Dehesa-Baeza, A.; Chan-Akeley, R.; Nguyen, P.; Zwibel, H. Cerebrospinal Fluid Interaction with Cerebral Cortex during Pediatric Abusive Head Trauma. J. Pediatr. Neurol. 2020, 18, 223–230.
- Toma, M.; Chan-Akeley, R.; Lipari, C.; Kuo, S.H. Mechanism of Coup and Contrecoup Injuries Induced by a Knock-Out Punch. J. Math. Comput. Appl. 2020, 25, 22.
- Toma, M.; Nguyen, P. Coup-contrecoup brain injury: Fluid-structure interaction simulations. Int. J. Crashworth. 2020, 25, 175–182.
- Toma, M. Predicting Concussion Symptoms Using Computer Simulations. Adv. Intell. Syst. Comput. 2019, 880, 557–568.
- Toma, M.; Kuo, S. Computational Assessment of Risk of Subdural Hematoma Associated with Ventriculoperitoneal Shunt Placement. Lect. Notes Comput. Vis. Biomech. 2020, 36, 36–47.
- Kwon, E.; Singh, M.; Vallabh, R.; Das, R.; Taylor, M.; Fernandez, J. Modelling ballistic cranial injury and backspatter using smoothed particle hydrodynamics. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018.
- Ho, A.; Tsou, L.; Green, S.; Fels, S. A 3D swallowing simulation using smoothed particle hydrodynamics. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2014, 2, 237–244.
- Harrison, S.; Eyres, G.; Cleary, P.; Sinnott, M.; Delahunty, C.; Lundin, L. Computational Modeling of Food Oral Breakdown Using Smoothed Particle Hydrodynamics. J. Texture Stud. 2014, 45, 97–109.
- Brandstaeter, S.; Fuchs, S.; Aydin, R.; Cyron, C. Mechanics of the stomach: A review of an emerging field of biomechanics. GAMM-Mitteilungen 2019, 42, e201900001.
- Sinnott, M.; Cleary, P.; Harrison, S. Peristaltic transport of a particulate suspension in the small intestine. Appl. Math. Model. 2017, 44, 143–159.
- Harrison, S.; Cohen, R.; Cleary, P.; Barris, S.; Rose, G. A coupled biomechanical-Smoothed Particle Hydrodynamics model for predicting the loading on the body during elite platform diving. Appl. Math. Model. 2016, 40, 3812–3831.
- Harrison, S.; Cleary, P.; Cohen, R. Dynamic simulation of flat water kayaking using a coupled biomechanical-smoothed particle hydrodynamics model. Hum. Mov. Sci. 2019, 64, 252–273.
- Fernandez, J.W.; Das, R.; Cleary, P.W.; Hunter, P.J.; Thomas, C.D.L.; Clement, J.G. Using smooth particle hydrodynamics to investigate femoral cortical bone remodelling at the Haversian level. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 129–143.
- Frissane, H.; Taddei, L.; Lebaal, N.; Roth, S. SPH modeling of high velocity impact into ballistic gelatin. Development of an axis-symmetrical formulation. Mech. Adv. Mater. Struct. 2019, 26, 1881–1888.