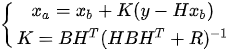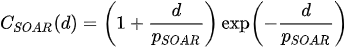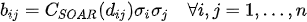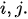| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Italia De Feis | + 1031 word(s) | 1031 | 2020-05-07 05:12:08 | | | |
| 2 | Camila Xu | -2 word(s) | 1029 | 2020-10-30 07:01:04 | | |
Video Upload Options
Thermal infrared remote sensing measurements are blinded to surface emissions under cloudiness because infrared sensors cannot penetrate thick cloud layers. Therefore, surface and atmospheric parameters can be retrieved only in clear sky conditions giving origin to spatial fields flagged with missing pieces of information. Motivated by this we present a methodology to retrieve missing values of some interesting geophysical variables retrieved from spatially scattered infrared satellite observations in order to yield level 3 (L3), regularly gridded, data. The technique is based on a 2-Dimensional (2D) Optimal Interpolation (OI) scheme. The goodness of the approach has been tested on 15-min temporal resolution Spinning Enhanced Visible and Infrared Imager (SEVIRI) emissivity and surface temperature (ST) products over South Italy (land and sea), on Infrared Atmospheric Sounding Interferometer (IASI) atmospheric ammonia (NH3) concentration over North Italy and carbon monoxide (CO), sulfur dioxide (SO2) and NH3 concentrations over China. Sea surface temperature (SST) retrievals have been compared with gridded data from MODIS (Moderate-resolution Imaging Spectroradiometer) observations. For gases concentration, we have considered data from 3 different emission inventories, that is, Emissions Database for Global Atmospheric Research v3.4.2 (EDGARv3.4.2), the Regional Emission inventory in ASiav3.1 (REASv3.1) and MarcoPolov0.1, plus an independent study.
1. Introduction
Infrared instrumentation on geostationary and polar-orbiting satellites are providing information at a very fine temporal and spatial resolution offering new possibilities for the monitoring of the environment, analysis of trends and patterns, forecasting, and air quality studies. Nevertheless, infrared sensors cannot penetrate thick cloud layers, so observations are blinded to surface emissions under cloudiness, and surface and atmospheric parameters can be retrieved only in clear sky conditions. To reconstruct a model of the field of interest for the entire surface and yield satellite products on a regular grid mesh, interpolation techniques and spatial statistics to deal with very large data sets are mandatory.
OI [1][2] is a multivariate statistical interpolation scheme used in data assimilation. In OI, we linearly combine two sources of information, an observation vector, and a background vector, according to their relative accuracies. The weights assigned to the observation increment (or innovation) are optimally determined to minimize the analysis error variance, and the estimate itself is unbiased (i.e., has the same mean as the true field). The knowledge of the autocovariance of the “true” process, partially given by observations, is fundamental to run the scheme because observations are weighted according to it. Generally, it is assumed to be homogeneous and isotropic. OI is equivalent[1][3] to a three-dimensional variational (3D Var) cost function approach and to the so-called kriging scheme[4]. The OI method has advantages over other methods because it is not necessary to find out independent data and reference data.
The goodness of the OI approach OI has been tested on SEVIRI emissivity and ST products over South Italy, on IASI NH3 concentration over Po-Valley region located in Northern Italy and CO , SO2 and NH3 concentrations over China. SST retrievals have been compared with gridded data from MODIS (Moderate-resolution Imaging Spectroradiometer) observations; gases concentration have been compared to data from EDGARv3.4.2, REASv3.1 and MarcoPolov0.1 emission inventories, in order to check the capability of the methodology to reveal hotspots or locations with persistent emissions. Moreover, for NH3 , we considered also an independent study[5].
2. Method
OI is based on the following interpolation equations, that define the optimal least-squares estimator, or Best Linear Unbiased Estimator (BLUE) estimator, which builds the update step of the system, that is, the analysis:
where the linear operator 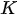
In the equations, 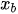
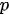

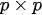
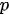

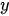
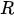
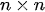
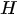
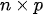
The most delicate point is the specification of B because the practical implementation of the scheme above is hampered by its size which is dramatically huge also for fields corresponding to Earth regions of a few kilometers. However, in general, in 3D Var, the spatial correlation structure of the model prior is assumed to be homogeneous and isotropic. These hypotheses are introduced to simplify the characterization of correlation functions, thus reducing them to a correlation model type and a correlation length (i.e., the length by which the correlation value decreased by a certain fixed value).
Moreover, the fundamental hypothesis in OI is that for each model variable, only a few observations are important in determining the analysis increment. These three assumptions permit to simplify the problem reducing to a local analysis whose main ingredients are:
-
for each analysis point xi consider a small number pi of observations using empirical selection criteria;
-
observations must be weighted according to distance from the considered analysis point.
The selection step in point 1. should in principle provide all the observations which would have a significant weight in the optimal analysis, that is, those which have significant background error covariances with the variable considered. In practice, background error covariances are assumed to be small for large separation, so that only the observations in a limited geometrical domain around the model variable need to be selected. Two common strategies for observation selection are pointwise selection and box selection. In pointwise selection, only observations within some cut-off radius with respect to the considered analysis point are taken into account; in box selection, for all the points in an analysis box, all observations located in a bigger selection box are considered, so that most of the observations selected in two neighboring analysis boxes are identical. Pointwise selection could produce spatial discontinuities in the analysis field, so box selection has to be preferred.
As regards the choice of the weights in point 2., in our set-up, we considered the Second Order AutoRegressive (SOAR) model[1][6] to build 
where 
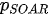
being 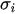
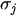
References
- Ac Lorenc; Analysis methods for numerical weather prediction. Quarterly Journal of the Royal Meteorological Society 1986, 112, 1177-1194, 10.1256/smsqj.47413.
- Daley, R.. Atmospheric Data Analysis; Cambridge University Press, Eds.; Cambridge, MA, USA: Cambridge, 1993; pp. 99-184.
- Wikle, C.K.; Berliner, L.M.; A Bayesian Tutorial for data assimilation. Physica D 2007, 230, 1-26, 10.1016/j.physd.2006.09.017.
- Cressie, N.. Statistics for Spatial Data; Wiley, Eds.; Wiley: New York, 1993; pp. 105-209.
- Van Damme, M.; Clarisse, L.; Whitburn, S.; Hadji-Lazaro, J.; Hurtmans, D.; Clerbaux, C.; Coheur, P.; Industrial and agricultural ammonia point sources exposed. Nature 2018, 564, 99–103, 10.1038/s41586-018-0747-1.
- Furrer, R.; Genton, M.G.; Nychka, D.; Covariance Tapering for Interpolation of Large Spatial Datasets. J. Comput. Graph. Stat. 2006, 15, 502-523, 10.1198/106186006X132178.