| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Wolfgang Orthuber | + 3014 word(s) | 3014 | 2020-04-29 06:04:37 | | | |
| 2 | Wolfgang Orthuber | -54 word(s) | 2960 | 2020-10-27 18:23:20 | | | | |
| 3 | Nicole Yin | Meta information modification | 2960 | 2020-10-29 05:02:29 | | | | |
| 4 | Nora Tang | Meta information modification | 2960 | 2020-11-10 07:44:29 | | |
Video Upload Options
This review focuses the exact and global definition of information (for unambiguous interpretation as mathematical object) and its digital application. New uniformly defined "domain vectors" (DVs), with structure "UL plus number sequence", are proposed. The "UL" is an efficient global pointer to the uniform online definition of the (after the UL) following number sequence. DVs are globally exactly defined, identified, interoperable, comparable, and (language independently) searchable by criteria which users can define online. The introduction of a compact DV data structure may substantially improve the digital representation of information.
1. Introduction
In terms of "information", the exact and complete concept is meant in this approach[1] and applied to digital information. There is a large amount of literature about information, but imprecise and unclear terms and concepts have been used for the definition of information. The consequence is ambiguity and inefficient approaches in digital information handling. This could be improved very much. For efficiency, also for the quantification of similarity and for the general comparison of information (and more), a clear, precise, and natural approach is necessary.
2. Exact definition of Information
Sets and functions resp. mappings on sets are used for definition of mathematical objects, they form the (clear and fruitful) basis of mathematics. It is only consistent to use these terms also for precise definition of information. Then information can be handled like other mathematical objects in well defined way. For definition of information, we recall that information is selection. It is well-known that any piece of digital information is a bit sequence and, therefore, a selection. Information, in general, as a result of any physical experiment, is also a selection (from a set of possible results; see, e.g., page 6 of Dirac's book[2]). The approach[1] proposed here consequently begins with this definition:
|
"Information is selection from a domain." |
(1) |
Here, "domain" denotes an ordered (one-dimensional or multidimensional) set of possibilities, which are common between the sender and receiver of the information. Information is always associated with a domain, which, in turn, is the domain of the information. The sender and receiver must both know the domain; for example, they must have a common vocabulary. Then, information is processed and transported digitally as a selection from the domain, as a number sequence. The domain of information crucially determines its digital representation. Therefore, information is fully defined by its domain and its selection from the domain[1][3][4][5].
It is important that (1) is a fundamental principle which is generally valid, even in elementary physics, and more research concerning this is recommended. For example, a common elementary charge and the derived common set (domain) of multiples of this elementary charge are preconditions for any electronic communication.
3. Global Definition of Information
Digital information consists of number sequences which are defined, by context, in a variable way. This can be improved by globally defining the domains of digital information (respective number sequences) in a uniform machine-readable way on the internet (i.e., as uniform online definitions of an ordered set). Let "Uniform Locator" ("UL") denote an efficient link to the online definition of the domain of the subsequent number sequence. The UL together with this number sequence is called a "domain vector" ("DV"):
|
DV: UL plus number sequence |
(2) |
The DV can be used to transport any globally defined digital information. The online definition of the domain is the global "predefinition" of the information [4]. As the DV contains the UL of this predefinition of the domain and the number sequence, which selects in this domain, the DV represents globally defined information. This domain of the DV is also called "adapted domain", because it can be adapted to any application.
3.1. Format of the Domain Vector (DV)
Using a hierarchical UL and self-elongating numbers, a very efficient binary format of the DV (2) is possible[1][4]. Though it is much more efficient than any format which can be edited by conventional text editors, it is possible to edit DVs in comfortable way by special editors which use the online definition. Because the online definition is machine readable and can be designed very detailed, also for editing of a DV very detailed additional explanatory information can be provided.
3.2. Literature Research
Usually, information is implicitly regarded as a selection from a set of possibilities (i.e., a domain). However, the global and uniform definition of this set is not focused. For an extensive literature review, Google Scholar[6] was used, with "Information" and "Definition" used as search terms, without any restrictions on publishing dates. A more restrictive search was also done, and other search engines were also used. Except for the author’s own publications, there were no relevant studies which focused on the definition of information using a global definition of a common set of possibilities or domain!
4. Examples and Application
Original information ORGINFO often is complex and multidimensional like an individual medical diagnosis. But even a much simpler one-dimensional example like "atmospheric temperature" shows the advantages of an adapted domain. Let's assume that we want a digital representation DIGINFO of a certain original value ORGINFO, e.g. 16 degree centigrade.
4.1. "Language Vocabulary" as Domain
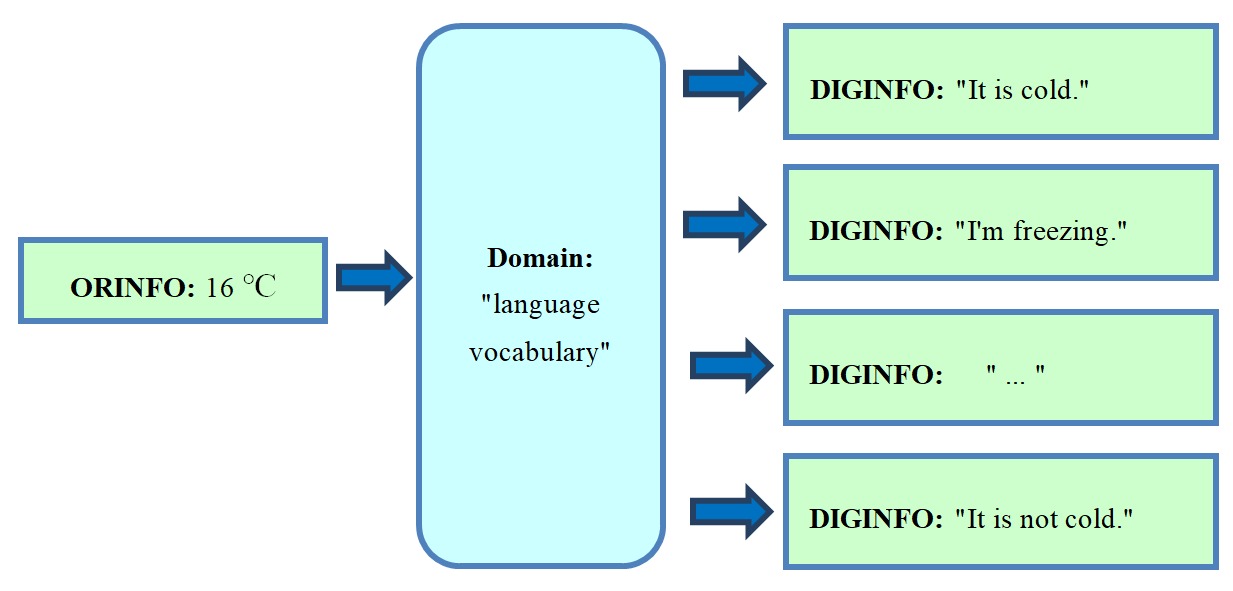
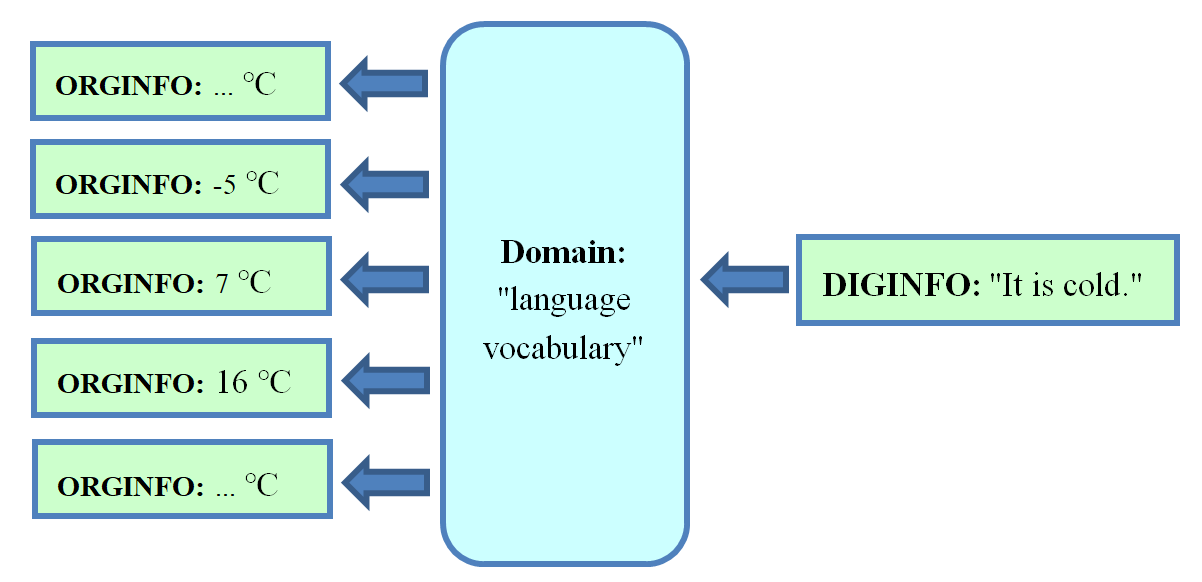
For language based DIGINFO we may use the string "air temperature is 16 degree centigrade". Typically this is communicated in less precise and variable way, using strings like "I am freezing" or "it is cold" or even "it is not cold", depending on constitution or clothes and depending on native language. This shows the complexity of information transport in case of "language vocabulary" as domain of the digital representation DIGINFO. Using numbers which select letters, DIGINFO selects elements of language vocabulary and combines them to get meaning. There is no bijection (no one-to-one mapping) from ORGINFO to its digital representation DIGINFO. Figure 1 and Figure 2 illustrate this in both directions[1].
Figure 1. Even if the domain "language vocabulary" of the same language is used, the original information (ORGINFO), e.g., "air temperature is 16°C", can be translated in several ways into its digital representation, digital information (DIGINFO). The results are imprecise.
Figure 2. Using the domain "language vocabulary", an exemplary text search of "It is cold" finds textual representations of very different original temperatures (ORGINFO).
Thus, in case of "language vocabulary" as domain there are many ways for coding ORGINFO digitally (Figure 1). At this usually original relevance and precision gets lost (Figure 2).
4.2. Adapted Domain
For a precise comparison and search of ORGINFO, a solution that is less variable and more reproducible than using "language vocabulary" as the domain of the digital representation DIGINFO is desirable. This is possible through the use of a topic-specific "adapted domain" which is the domain of the above introduced DV (2). It can be adapted to any application. It is defined online (i.e., globally), such that there is full reproducibility in both directions—that is, it forms a bijection (a one-to-one correspondence) between ORGINFO and its digital representation DIGINFO. As it is impossible to bijectively represent "all information" (i.e., "all features") of reality digitally, the restriction to relevant features (i.e., sub-areas of all information) is necessary. This is possible because ORGINFO is communicated within a certain topic—that is, it should only represent features which are relevant within the chosen topic. Thus, for the adaptation of the domain of ORGINFO to this topic, the following questions are (repeatedly) asked[1]:
a) Which (additional) independent feature (parameter) is relevant within the chosen topic?
If an appropriate quantification of this feature is available online, reuse it; otherwise, ask:
b) Which variants of the feature are possible? Quantify the feature, order its variants, and define a bijection to the numeric values of a parameter with the corresponding order.
For a), relevant independent features are repeatedly searched. Every feature has variants which are selected (represented) by ORGINFO. If these are naturally ordered (e.g., have a quantitative magnitude), this order is taken; otherwise, a useful order is introduced. If the resulting order is multidimensional, every dimension can be regarded as an independent feature with a one-dimensional order.
After this, every resulting feature has a one-dimensional set of variants, such that every variant of every feature is bijectively represented (i.e., digitally selected) by a single number. Thus, the feature is quantified. If "N" denotes the count of all features, then the selection of the variants of all features is done digitally using N numbers (i.e., by an N-dimensional vector). The conversion of ORGINFO to this digital representation DIGINFO is a bijection into an N-dimensional vector space (i.e., the digital domain of DIGINFO) from the (to the topic) adapted domain of ORGINFO. Due to this bijection, the domains of ORGINFO and DIGINFO can be treated as equivalent. This substantially simplifies our considerations in the case of adapted domains.
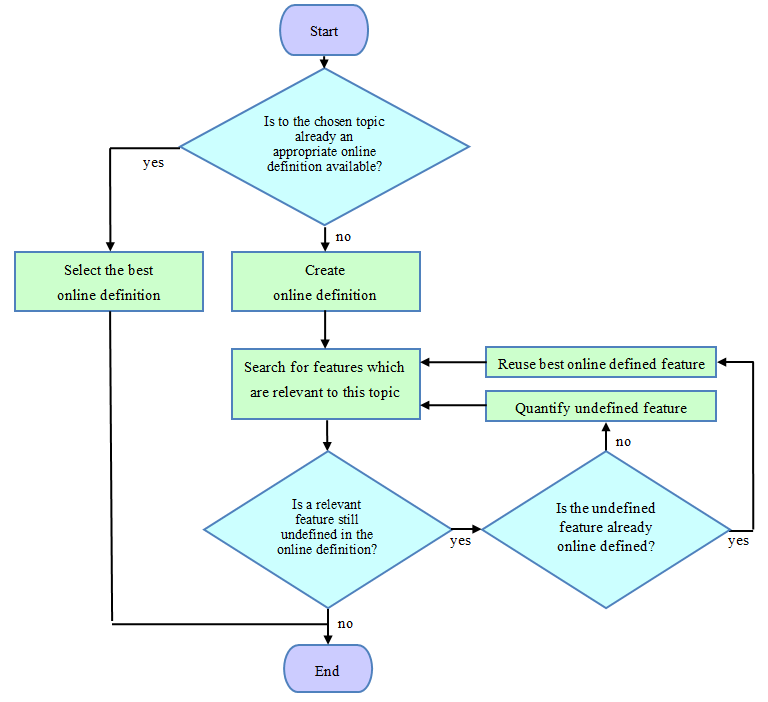
Within the adapted domain, the relevant features of the original information are represented by numbers. Therefore, the definition of an adapted domain can be regarded as the definition of the number sequence, DIGINFO, which represents certain relevant features within the chosen topic. Adapted domains can be defined online[1]. It is important that online definitions are globally available and can be defined to any topic. To avoid redundancy, appropriate online definitions for this topic should be first searched and used before a new definition is defined. If relevant features are still undefined, their new online definition is appropriate. Figure 3 shows a flowchart of the online definition of an adapted domain.
Figure 3. Online definition of an adapted domain[1].
Consider this process applied to the above one-dimensional domain "air temperature" of ORGINFO. It can be seen as subset within a multidimensional domain "weather data" to the topic "weather". We assume that no appropriate online definition to the topic "weather" is available. In this case, the generation of a new definition is appropriate. According to Figure 3, independent relevant features within the topic "weather" are searched. There are many such features, such as air temperature, barometric pressure, relative humidity, and so on. In this example, only the feature "air temperature" is necessary. If an appropriate online definition is available, it is used; otherwise, such a definition is created. For this, the feature is quantified. In this example, the original information (ORGINFO) "air temperature" already has the internationally given ordered property T °C. Therefore, simply the number T (which represents multiples of °C) is taken as the digital information (DIGINFO). Thus, all interesting variants of this feature are ordered to obtain a one-to-one correspondence (bijection) with the number T. This is illustrated in Figure 4.
Figure 4. The original information (ORGINFO) "air temperature is 16°C" is translated bijectively to its digital representation, DIGINFO. It is identified by the "Uniform Locator" ("UL"), which, according to (2), is an efficient global pointer to the online definition of the adapted domain. Due to the use of the adapted domain "multiples of °C", there is a one-to-one correspondence of every variant of ORGINFO to its digital representation, DIGINFO[1].
Figure 4 shows a clear one-to-one correspondence between every possible variant of ORGINFO to its digital representation, DIGINFO. In contrast, Figure 1 and Figure 2 show how ambiguity and imprecision occurs, in the case of free language, due to the use of the domain "language vocabulary".
As shown above for the feature "atmospheric temperature", definitions of further features such as "GPS coordinates", "barometric pressure", "relative humidity", and so on can be appended to the online definition of the domain "weather data". This increases its dimensionality and the maximal length of the number sequence DIGINFO. If the value of a certain number is not available, it can be represented, for example, by a short placeholder in DIGINFO.
At present (2020), such multidimensional quantitative data are often the content of databases. There are already many databases which work with "locally defined adapted domains". In particular, if they contain quantitative measurable data, there is often already a bijection between ORGINFO and DIGINFO. For the global comparability of information, however, a global definition of the domain is also important. Therefore, every "adapted domain" is defined online and, thus, is globally valid. Existing databases can retrospectively provide such online definitions for the domains of their data in order to ensure the global comparability of their data.
4.3. Comparison and Search of Information
4.3.1. Text Search of Information
In the case of a text search, the domain is "language vocabulary". As shown above, there is no bijection between the original information (ORGINFO) and the digital representation, DIGINFO, in this case and, thus, the comparability of the original information ORGINFO is limited or lost. Thus, as a matter of principle, the value of a text search is limited.
Special ontologies have been developed to obtain a better adaptation to applications, such as in medicine (e.g., ICD[7] and SNOMED CT [8][9]). Such ontologies can be seen as discrete domains. If they are (without legal restrictions) freely available [4], these can serve as starting points for the online definition of diagnosis-specific adapted domains, which are suitable for decisional support.
4.3.2. Similarity Search of Information
Similarity searches have been well analyzed in the literature [10][11], as well as for medical databases [12][13][14]. In a similarity search, certain searched information is provided, and it is required that the most similar digital representations are listed first in the search results. This means that the searched information is compared with every occurrence that contains possibly interesting digital information (DIGINFO) using a distance function F, which provides, as a result, a number which reproducibly shows the rank of the DIGINFO in the search result. As not only the similarity search of a certain digital number sequence, or DIGINFO, but also the similarity search of original information ORGINFO is desirable, an adapted domain is necessary. The online definition of the adapted domain also contains the definition of the distance function F and ensures that there is a bijection from ORGINFO to DIGINFO. Thus, the smaller the value of the distance function F(SEARCHED_DIGINFO, DIGINFO) is, the higher the rank of DIGINFO and of corresponding ORGINFO will be in the search results.
Similarity searches are, at present, typical applications in databases [15]. If such databases provide online definitions of the domains of their data, they can make these data globally comparable and accessible for global searches.
4.4. User-Defined Global Similarity Search of Information
Now, we have a theoretical basis for conducting similarity searches on original information (ORGINFO). To obtain a bijection with its digital representation DIGINFO, the first step is the definition of a topic-specific adapted domain of ORGINFO (as shown in Figure 3). As described above, we repeatedly carry out the following two steps:
a) Ask for relevant features within the chosen topic;
b) Quantify them, reusing already existing online definitions.
For this, expert knowledge in the chosen field is necessary. Therefore, it is important that the users—especially experts in a certain topic—can define terms in this topic in the adapted domain with the topic-specific relevant features that they want as search criteria. The use of relevant features as criteria for similarity searches has been, up to now, a typical application in databases [15][16][17]. This restriction, however, is not necessary. After standardized online definition and global identification by UL within a domain vector (2), such features (definable by users) become globally searchable [1][4]. Nevertheless, this important possibility for information retrieval has not yet been realized.
5. Urgent Questions in Information Science and Informatics (2020)
At present, a lot of vague and inefficient approaches about "information" are discussed and partially focused, but the exact approach (1) and the global definition (2) are still neglected. This has relevant consequences, therefore it is appropriate to list here some more and more pressing questions:
1. Why has the exact definition of information as a selection from an ordered set (or domain) (1) not been consequently emphasized and technically utilized from the beginning? This is far-reaching, as adapted domains can be defined online for all possible applications (Figure 3). If it is unclear how to define an ordered set (i.e., domain) and the numbers that select from this set, advanced training is necessary—information experts (by definition) need to know about this. A "language vocabulary" is only one example of a domain. Semantic concepts and other a posteriori combinations of information are derived applications and also need a basis.
2. Why can users (especially professionals, experts, and specialists) not define adapted domains online for precise language-independent global communication in their areas of expertise?
3. Digital information consists of number sequences. Why have these, up to now, been defined in variable and complex ways by context? Why have globally defined, identified, and searchable information carriers (such as the domain vectors detailed above (2), up to now, not been introduced (as selections from an online defined adapted domain), decades after the introduction of the internet?
4. Why are global information searches still essentially restricted to text searching?
It should be clear that such restrictions have enormous adverse effects (e.g., in medicine). Generally, in professional areas, precise global comparability and precise neutral searches for information would be very advantageous. As preparation for this, the introduction of domain vectors (2), as globally defined searchable information carriers, would be an important step.
6. Conclusions
The domain of information is crucial for the digital representation of original data. User-guided online definitions of adapted domains for typical topics resp. applications (e.g., in medicine, science, industry) prepare information for similarity comparisons, considering decision-relevant criteria and features which are interesting for users.
Therefore, the introduction of domain vectors or DVs (2), as globally defined searchable information carriers, is recommendable. A first step for this is the establishment of an attractive online presence where users (e.g., experts in medicine and industry, scientists) can globally, and in a language-independent manner, define adapted domains and domain vectors (DVs) in their areas of expertise. This allows for a user-defined similarity comparison and information searches.
Furthermore, online definitions of DVs can also define global software interfaces (and DVs efficiently transport the data between these). This allows for the global programming and optimization of modular designs.
References
- Wolfgang Orthuber; Information Is Selection—A Review of Basics Shows Substantial Potential for Improvement of Digital Information Representation. International Journal of Environmental Research and Public Health 2020, 17, 2975, 10.3390/ijerph17082975.
- Dirac, P.A.M.. The Principles of Quantum Mechanics (No. 27); Oxford University Press: Oxford, UK, 1981; pp. 6.
- Wolfgang Orthuber; How to make medical information comparable and searchable. Digital Medicine 2020, 6, 1, 10.4103/digm.digm_4_20.
- Wolfgang Orthuber; Global predefinition of digital information. Digital Medicine 2018, 4, 148, 10.4103/digm.digm_28_18.
- Wolfgang Orthuber; Online definition of comparable and searchable medical information. Digital Medicine 2018, 4, 77, 10.4103/digm.digm_5_18.
- Anne-Wil Harzing; R Van Der Wal; Google Scholar as a new source for citation analysis. Ethics in Science and Environmental Politics 2008, 8, 61-73, 10.3354/esep00076.
- Toni Henderson; Jennie Shepheard; Vijaya Sundararajan; Quality of Diagnosis and Procedure Coding in ICD-10 Administrative Data. Medical Care 2006, 44, 1011-1019, 10.1097/01.mlr.0000228018.48783.34.
- Alessandro Longheu; Vincenza Carchiolo; Michele Malgeri; Medical Data Integration with SNOMED-CT and HL7. Advances in Intelligent Systems and Computing 2015, 353, 1165-1171, 10.1007/978-3-319-16486-1_115.
- Olivier Bodenreider; Ronald Cornet; Daniel J. Vreeman; Recent Developments in Clinical Terminologies — SNOMED CT, LOINC, and RxNorm. Yearbook of Medical Informatics 2018, 27, 129-139, 10.1055/s-0038-1667077.
- Daniel A. Keim; Efficient geometry-based similarity search of 3D spatial databases. ACM SIGMOD Record 1999, 28, 419-430, 10.1145/304181.304219.
- Zezula, P.; Amato, G.; Dohnal, V.; Batko, M. Similarity Search: The Metric Space Approach; Springer Science &Business Media, Inc.: New York, NY, USA, 2006; Volume 32.
- Philip Korn; Nicholaos D. Sidiropoulos; Christos Faloutsos; Eliot L. Siegel; Zenon Protopapas; Fast and effective similarity search in medical tumor databases using morphology. Photonics East '96 1996, 2916, 116-129, 10.1117/12.257282.
- E.G.M. Petrakis; Christos Faloutsos; Petrakis E.G.M.; Faloutsos C.; Similarity searching in medical image databases. IEEE Transactions on Knowledge and Data Engineering 1997, 9, 435-447, 10.1109/69.599932.
- Marc Wichterich; Philipp Kranen; Ira Assent; Thomas Seidl; Claudia Plant; Christian Böhm; Efficient EMD-based Similarity Search in Medical Image Databases. Science, Engineering, and Biology Informatics 2010, 6, 175-201, 10.1142/9789814307710_0009.
- Wei Lu; Jiajia Hou; Ying Yan; Meihui Zhang; Xiaoyong Du; Thomas Moscibroda; MSQL: efficient similarity search in metric spaces using SQL. The VLDB Journal 2017, 26, 829-854, 10.1007/s00778-017-0481-6.
- Xifeng Yan; Feida Zhu; Philip S. Yu; Jiawei Han; Feature-based similarity search in graph structures. ACM Transactions on Database Systems 2006, 31, 1418-1453, 10.1145/1189769.1189777.
- Li Liu; Mengyang Yu; Ling Shao; Unsupervised Local Feature Hashing for Image Similarity Search. Continuous-Time Distributed Policy Iteration for Multicontroller Nonlinear Systems 2015, 46, 2548-2558, 10.1109/tcyb.2015.2480966.