| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Kyuman Lee | + 1882 word(s) | 1882 | 2020-04-29 12:03:45 | | | |
| 2 | Kyuman Lee | Meta information modification | 1882 | 2020-04-30 06:31:47 | | | | |
| 3 | Kyuman Lee | Meta information modification | 1882 | 2020-04-30 06:32:30 | | | | |
| 4 | Camila Xu | Meta information modification | 1882 | 2020-04-30 07:30:47 | | | | |
| 5 | Camila Xu | -7 word(s) | 1875 | 2020-10-30 10:13:18 | | | | |
| 6 | Camila Xu | Meta information modification | 1875 | 2020-10-30 10:14:51 | | |
Video Upload Options
In visual-inertial odometry (VIO), inertial measurement unit (IMU) dead reckoning acts as the dynamic model for flight vehicles while camera vision extracts information about the surrounding environment and determines features or points of interest. With these sensors, the most widely used algorithm for estimating vehicle and feature states for VIO is an extended Kalman filter (EKF). The design of the standard EKF does not inherently allow for time offsets between the timestamps of the IMU and vision data. In fact, sensor-related delays that arise in various realistic conditions are at least partially unknown parameters. A lack of compensation for unknown parameters often leads to a serious impact on the accuracy of VIO systems and systems like them. To compensate for the uncertainties of the unknown time delays, this study incorporates parameter estimation into feature initialization and state estimation. Moreover, computing cross-covariance and estimating delays in online temporal calibration correct residual, Jacobian, and covariance. Results from flight dataset testing validate the improved accuracy of VIO employing latency compensated filtering frameworks. The insights and methods proposed here are ultimately useful in any estimation problem (e.g., multi-sensor fusion scenarios) where compensation for partially unknown time delays can enhance performance.
1. Introduction
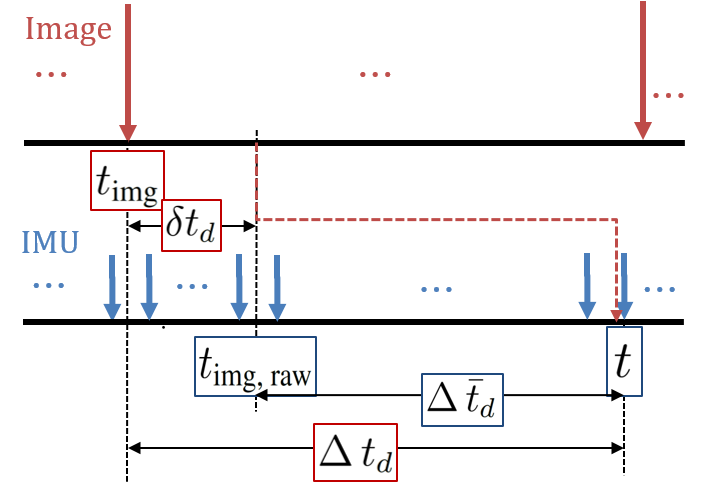
The most widely used algorithms for estimating the states of a dynamic system are a Kalman Filter [1][2] and its nonlinear versions (e.g., extended Kalman filter (EKF) [3][4] and unscented Kalman filter (UKF) [5]). The design of the standard Kalman filter does not inherently allow for significant sensor-related delays in computation. Figure 1 shows that the delay is the time difference between an instant when a measurement is taken by a sensor and another instant when the measurement is available in the filter. As an example of key delay sources, some complex sensors such as vision processors for navigation often require extensive computations to obtain higher-level information from raw sensor data. Furthermore, a closed-loop system including control logic may be an overall computational burden to a single processor. Delays resulting from heavy computation may distort the quality of state estimation since a current measurement is compared to past states of a system model. In other words, unless compensating delays in Kalman filtering, large estimation errors may accumulate over time, or even cause the filter to diverge.
The delay value is typically at least partially unknown and at least partially variable in many real applications. As an example of delay uncertainty contributors, even though a local clock is initially forced to synchronize with the centralized clock, deviations between clocks would occur because of clock drift, skew, or bias. In sensor fusion systems, when the timestamps of each sensor are typically recorded by triggered signals, non-deterministic, or non-quantized transmission delays lead to unknown time offsets on sensor streams. Moreover, if low-cost sensors such as rolling shutter cameras or software triggered devices are mounted on a vehicle, the variance of the uncertainty of timestamps might be larger. In particular, in visual-inertial odometry (VIO), we do not know the exact time instant when a camera opens and captures images for any particular pixel location. Often, exposure time depends on surrounding illumination conditions. The timestamp of the latest image by some cameras corresponds to some event such as when the shutter was triggered to start or when the entire image was available in memory. In practice, these uncertainties may be small compared to traditional sensors used for feedback in aerospace applications—but can be a major contributor to errors in emerging estimation problems such as VIO. Indeed, when estimating faster motions such as a highly agile unmanned aerial vehicle (UAV) or using progressive scan cameras, the unknown time delays may be a major driver of navigation quality and achievable controller bandwidth. We have experimentally observed the necessity of the time delay compensation to be more accurate than typically demanded, specifically for a UAV flying closed-loop on a vision-based navigation solution. With poor time delay compensation, we have observed oscillations and even divergence of estimates and closed-loop tracking error as expected, but even when we use fixed/known time delay compensation, we find time delay is still a limiting factor in accuracy and achievable control bandwidth. To illustrate, consider a UAV with a body-fixed camera that maneuvers with a more rapid rotation than reference design. Any time error produces a larger potential position estimation error with this faster rotation. Thus, even after the very best job possible has eliminated as much deterministic time delay error as is practical, we find that adapting to the non-deterministic error can enhance performance. In particular, we find it can be beneficial to deal with unknown time delays in VIO systems used in closed flight control and other systems like these.
To fuse visual measurements with unknown time delays in VIO systems and systems like them (e.g., multi-sensor fusion), the approach in this paper incorporates three correction techniques into state estimation. First, we directly estimate the unknown part of actual delays in online fashion by augmenting vehicle-feature states. With the estimated unknown part and the approximately known part of the delays, we find the most precise measurement times based on the definition of total delays introduced in this paper. Next, at the calibrated measurement time, we evaluate the Jacobian and the residual for the EKF using interpolated states. At the measurement update of the EKF, the third correction is to formulate a modified Kalman gain by the cross-covariance term computed during the delay period. The testing results of this study on flight datasets show that the proposed latency compensated VIO is a more reliable and accurate navigation solution than the existing VIO systems.
2. Definition of Time Delays
Latency is the time difference between when an image was grabbed and when vision data from the image are updated in the filter, shown in Figure 1.
That is, true delays 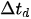
where 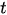
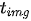
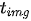
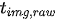
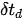
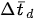
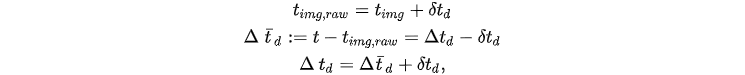
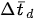
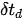
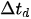
3. Approximately Known Part of Time Delays
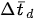
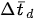
Cross-Covariance—“Covariance Correction”
During the delay period, even though an image was already captured in the past, since vision data from the image have not yet arrived at the filter, the EKF is not able to perform the measurement update. Indeed, the filter processes only time update. When a vision data packet from the image finally arrives and is ready to update in the filter, we simply execute the Jacobian and residual correction in Equations using the delayed measurements. However, unlike the baseline correction, if the filter updates as if the measurements arrive immediately without delays (like red lines in Figure 2), then the filter can achieve a more accurate estimate. In fact, covariance correction presented in this section (like blue lines in Figure 2) is as if the filter accomplished the general measurement update at the time instant when the image was captured. In other words, red lines in Figure 2 are ideal but unrealistic, and blue lines in Figure 2 are practical. The red lines process the measurement update first and then time update; however, the order of the processes of the blue lines is the opposite. Only the order of the processes has changed.
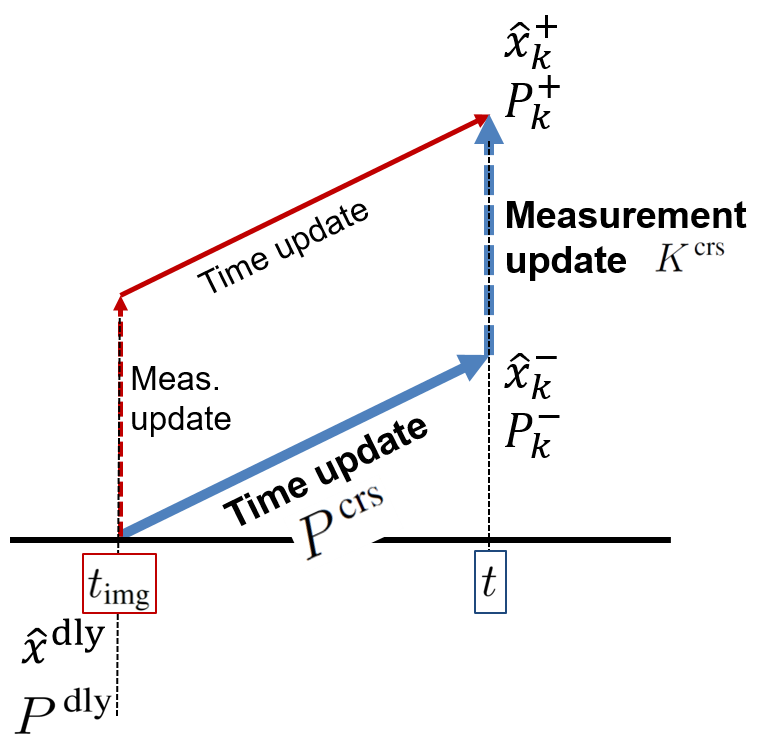
Figure 2. A schematic of a modified measurement update using covariance correction.
Among a variety of fusing techniques for time-delayed observations, the stochastic cloning [5]-based method (i.e., the Schmidt EKF [6]) is applicable to varying delays and nonlinear functions such as the vehicle and camera models, respectively. Thus, this study modifies the method for finding the optimal navigation solution of vision-aided inertial navigation systems.
4. Unknown Part of Time Delays
Although residual, Jacobians, and covariance are corrected for measurements with time delays, if 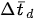
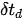
Figure 3 shows three corrections in the latency compensated VIO presented in this study. From the standard Kalman filter, if one does not account for time delay, propagation, and measurement update look like grey lines in Figure 3. For the last correction, we estimate the unknown part of time delays to obtain more precise time instant when the delays begin. As discussed in Introduction, unknown phenomena such as clock bias, drift, skews, and asynchronization cause 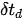
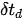
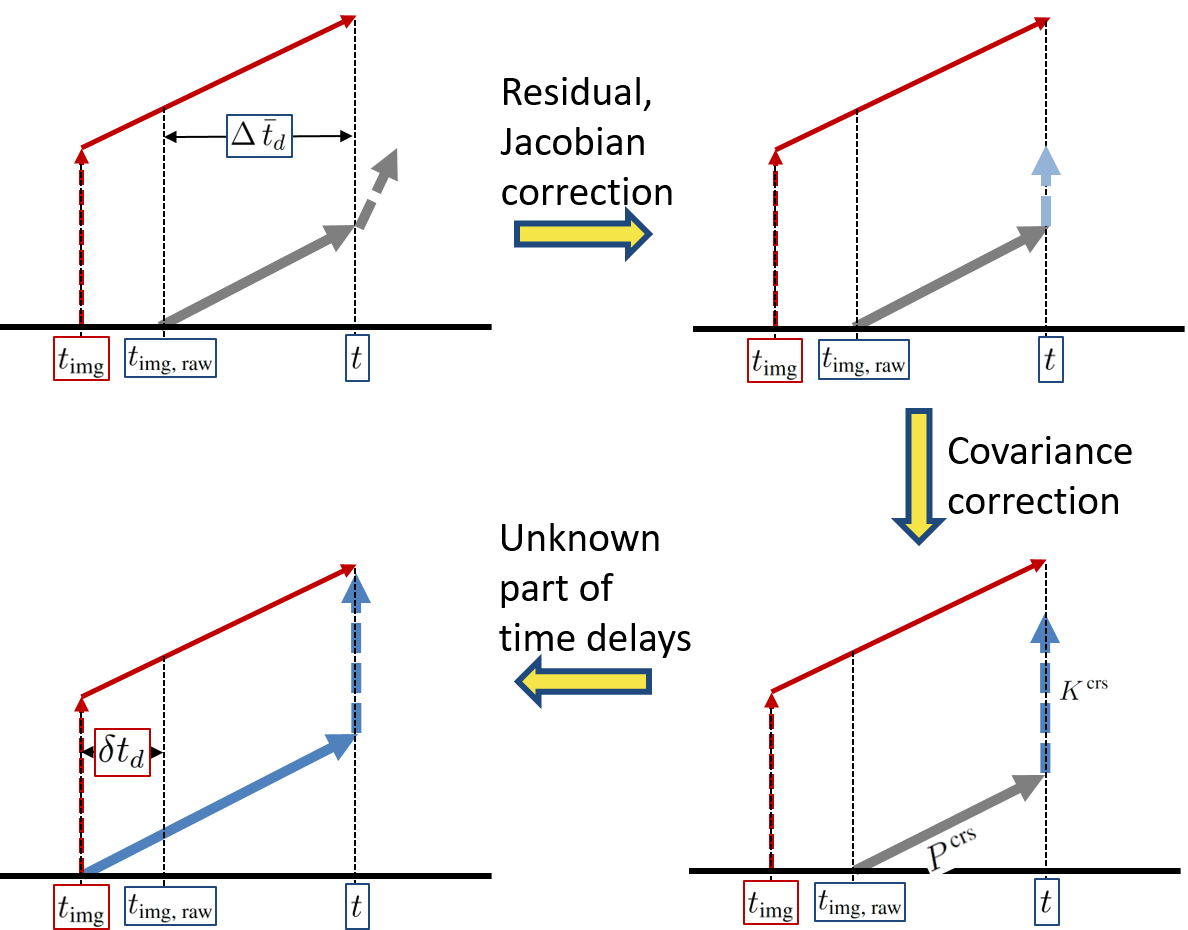
Figure 3. Three corrections in the latency compensated VIO.
Here, let us call the combination of the estimation of the unknown latency in this section with the baseline correction “online calibration.” Therefore, to reliably estimate the state variable and effectively compensate the total delays, we incorporate all three corrections, called “latency-adaptive filtering.”
This section summarizes and describes an implementation of the proposed method. Figure 4 illustrates a flow chart of the overall process.
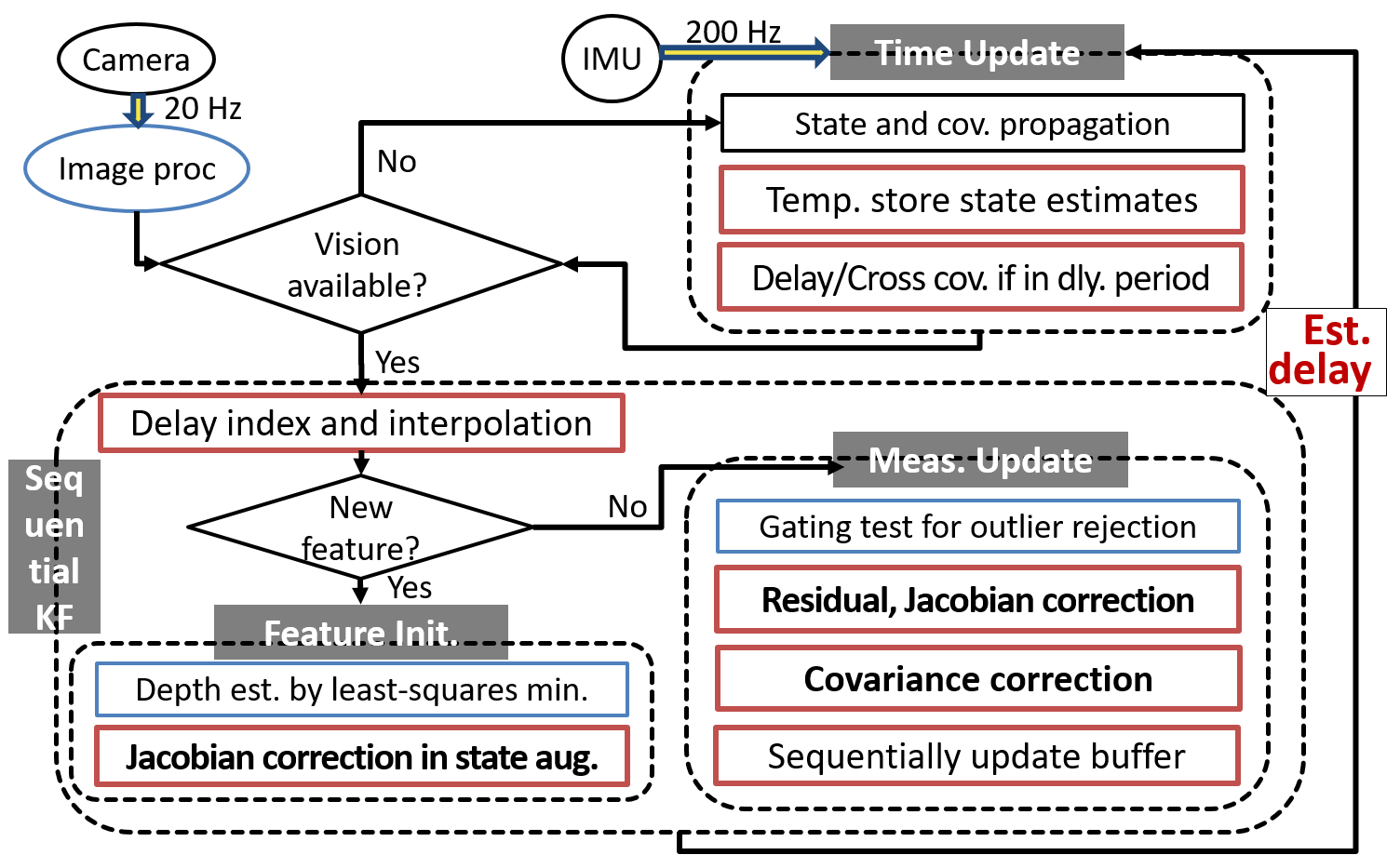
Figure 4. A flow chart of the overall process of the latency compensated VIO.
5. Discussion
This study develops a practical extended Kalman filter (EKF)-based visual-inertial odometry (VIO) accounting for vehicle-feature correlations; that is, we develop tightly-coupled VIO for autonomous flight of unmanned aerial vehicles (UAVs). In particular, this paper has presented the development of a reliable and accurate filtering scheme for measurements with unknown time delays. We define time delays of vision data measurements in VIO. For compensating delayed measurements and estimating unknown delay values, this paper presents latency compensated filtering that includes state augmentation, interpolation, and residual, Jacobian, covariance corrections. The optimality of the three corrections and the observability of the state augmentation are validated; in other words, the appendix shows that the proposed latency compensated filter results in optimal estimates as if there were no delays in the data.
We test the performance of VIO employing the latency compensated filtering algorithms in the benchmark flight datasets for comparison to other state-of-the-art VIO algorithms. Results from flight datasets testing show that the novel navigation approach in this paper improves the accuracy and reliability of state estimation with unknown time delays in VIO. With the latency compensated filtering, the root mean square (RMS) errors of estimation are decreased. In particular, we show improved accuracy of our method over previous approaches for state estimation in the fast motion datasets.
The overall approach in this document can be easily employed in other filter-based, sensor-aided inertial navigation frameworks and is suitable to monocular VIO although this study uses a stereo camera to showcase the methods. Although the reliability and robustness of this study are validated by testing benchmark flight datasets, validating with other datasets is of interest.
References
- Tong Qin; Shaojie Shen; Online Temporal Calibration for Monocular Visual-Inertial Systems. 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 2018, ., 3662-3669, 10.1109/iros.2018.8593603.
- Mingyang Li; Anastasios I. Mourikis; Online temporal calibration for camera–IMU systems: Theory and algorithms. The International Journal of Robotics Research 2014, 33, 947-964, 10.1177/0278364913515286.
- Kyuman Lee; Eric N. Johnson; State and parameter estimation using measurements with unknown time delay. 2017 IEEE Conference on Control Technology and Applications (CCTA) 2017, ., 1402-1407, 10.1109/ccta.2017.8062655.
- Stergios I. Roumeliotis; Joel W. Burdick; Stochastic cloning: a generalized framework for processing relative state measurements. Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292) 2003, 2, 1788-1795, 10.1109/robot.2002.1014801.
- Stanley F. Schmidt; Application of State-Space Methods to Navigation Problems. Advances in Control Systems 1965, 3, 293-340, 10.1016/b978-1-4831-6716-9.50011-4.
- Kyuman Lee; Eric N. Johnson; Multiple-Model Adaptive Estimation for Measurements with Unknown Time Delay. AIAA Guidance, Navigation, and Control Conference 2017, ., 1260, 10.2514/6.2017-1260.