
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Orchidea Maria Lecian | -- | 2775 | 2024-11-07 20:36:34 | | | |
| 2 | Catherine Yang | -412 word(s) | 2363 | 2024-11-08 01:40:51 | | |
Video Upload Options
The Kottler-Schwarzschild-Kiselev blackhole spacetimes are analytically studied. The instances of the gtt components of the metric tensor are considered, where it contains a linear term, a cosmological constant, and both a linear term and a cosmological constant, in the deSitter determination and in the anti-deSitter one. The Birkhoff theorem is proven to be obeyed. The infinite-redshift surfaces are written. The parameter space of the models which constrain the blackhole mass are analytically spelled out. The coordinate-singularity-avoiding coordinates transformations are newly found. The possibility to obtain a scheme geometrically-mimicking quintessence is ruled out. The weak-field limit is studied from the appropriate Christoffel symbol. The quantum regime is envisaged.
1. Introduction
The Kottler-Schwarzshild-Kiselev blackhole spacetimes [1][2] are analytically studied after [3].
The Schwarzshild-deSitter blackhole spacetimes are newly investigated as far as the constraints on the blackhole mass is concerned. The pioneering works of [4] are here completed. The analysis is extended to the Schwarzschild-anti-deSitter blackhole spacetimes.
The generalized Schwarzschild blackhole spacetimes with a linear term are analyzed. The new constraints for the parameter space which defines the blackhole mass is analytically explored. The new constraints on the blackhole mass are worked out; the comparison is brought between the model and other Astrophysical objects.
The generalized Schwarzschild spacetimes with a linear term and a cosmological constant are newly investigated. The parameter space which defines the black hole mass is newly set and constrained.
The Kottler-Schwarszchild-Kiselev metric is proven to obey the Birkhoff Theorem. The occurrence that some of the terms qualifying the metric tensor be geometrically mimicking the presence of quintessence is ruled out.
The surfaces of infinite redshift are written. The coordinate-singularity-avoiding coordinate transformations are provided with. The weak-field limit is posed. The quantum implementation is envisaged. The present study is apt for the comparisons with the generalized Reissner-Nordstrom spacetimes as approached in [5]. The paper is organized as follows. In Section 2, the introductory material is exposed, which frames the present study within the previous achievements and the prospective applications. In Section 3, the Birkhoff theorem for the Generalized Schwarzschild spacetimes metric is proven. The possibility that the geometrical terms could mimic the role of quintessence is excluded after the analysis of the Einstein Field Equations (EFE’s). In Section 4, the Schwarzschild-deSitter spacetimes are recalled after the analyses of Nariai. In Section 5, the generalized Schwarzschild spacetimes with a cosmological-constant term are newly studied. In Section 6, the generalized Schwarszchild spacetimes with a linear term are newly explored. In Section 7, the generalized Schwarzschild Spacetimes with a linear term and a cosmological constant are newly investigated. In Section 8, the weak-field limit of the generalized Schwarszchild spacetimes is demonstrated from the opportune Christoffel symbol. In Section 9, the discussion about the experimental validations is presented. In Section 10, the needed remarks are exposed.
2. Introductory Material
In the present paper, the prescriptions of [6] are applied, according to which the matter is never put in the metric tensor, not even in the ultra-Relativistic limit.
One of the aims of the present paper is to establish the complete constraints between the blackhole mass and the value of the cosmological constant in the Schwarzschild-deSitter case to complete the pioneering work of [4], motivated after [7]; the study of the generalized Schwarzschild-deSitter spacetimes was further pursued in [8][9][10], and in [11] the coordinate-singularity-avoiding coordinate extensions are written.
Moreover, in the present analysis, the constraints on the blackhole mass in the Schwarzschild-anti-deSitter case will be newly set.
In the generalized Schwarzschild spacetimes with a linear term, it is possible to scrutinize the role of the linear term. More in detail, the addends in the left-hand side of the EFE’s related to the linear term do not mimic the presence of quintessence: it is straightforward to calculate that in general, the radial and transverse pressures are different. It is nevertheless possible to interpret the presence of the linear term as ’mimicking some kind of anisotropic fluid matter'; thus, a ’geometrical quintessence effect’ can be ruled out because the equation of state p = ωρ assumes that the pressure be isotropic.
One further purpose of the present work is to establish further constraints between the blackhole mass and the parameters qualifying the linear term. Moreover, it is possible to enhance the comparison between the role of the linear term and the parameters of spinning-blackhole spacetimes. In [12], a function of the scalar polynomial curvature invariants is written containing linear-term-related components. Ibidem, the relations between the linear term and the parameters qualifying spinning-blackhole spacetimes are reported.
The study of generalized Schwarzschild spacetimes with a linear term and a cosmological constant in the gtt component of the metric tensor is motivated after the studies [13] and after the further investigation [14][15][16].
3. The Birkhoff Theorem for the Generalized Schwarzschild Spacetimes Metric
Generalized Schwarzschild spacetimes are written according to the line element
where  is the generalization of the Schwarzschild term, qualified after the functional dependence on the function ψ(r).
is the generalization of the Schwarzschild term, qualified after the functional dependence on the function ψ(r).
The Ricci tensor Rµν is obtained as

The Ricci scalar R is found as

The Einstein FIeld Equations are written as

the matter is not put in the metric tensor, as indicated from [6].
From the tt component of the EFE's and from the rr component of the EFE's, the new constraint is secured
From the θθ component of the EFE’s and from the φφ component of the EFE’s, the new constraint is procured
4. The Schwarzschild-deSitter Spacetimes
The spherically-symmetric Schwarzschild-deSitter (Nariai) spacetimes, endowed with a Schwarzschild solid-angle element, are defined after the g tt element g tt =1 −rs/r−(Λ/3) r2 as

An upper bound of the mass M of a black-hole solution of a Schwarzschild-deSitter spacetimes from the value of the cosmological-constant term was found
in [4] as a function of Λ as![]() An upper bound of the mass M of a black-hole solution of a Schwarzschild-deSitter spacetimes from the value of the cosmological-constant term was found in [4] as a function of Λ as
An upper bound of the mass M of a black-hole solution of a Schwarzschild-deSitter spacetimes from the value of the cosmological-constant term was found in [4] as a function of Λ as
![]()
The results of [11] are here reviewed for comparison with the further findings of the present paper, and appropriately scrutinised. The choice of the Kruskal coordinates is apt to write the maximal extension of the metric Equation (8). The following coordinate-singularity-avoiding coordinate extensions (u,v) is shown from [11] as

with the radial variable defined after the differential dρ as

thus with ρ 0 = 0, r 0 = 0
The Nariai coordinates Equation (9) read

where the variable ρ is defined after Equation (10) and it reads

with the opportune choice of the initial values of the variables.
The quantity T in Equation (11) is needed as

where the absolute value of the cosmological-constant parameter is taken, in order to show the integration of Equation (10) as Equation (11) within the chosen order(s) of infinitesimals.
k is calculated after the following equation

the different orders of infinitesimals can be chosen for the modifications of the Schwarzschild radius to be small.
The latter condition implies

5. The Schwarzschild Spacetimes with a Cosmological Constant
The generalized spherically-symmetric Schwarzschild spacetimes with a cosmological-constant term, endowed with a Schwarzschild solid-angle element, are written as
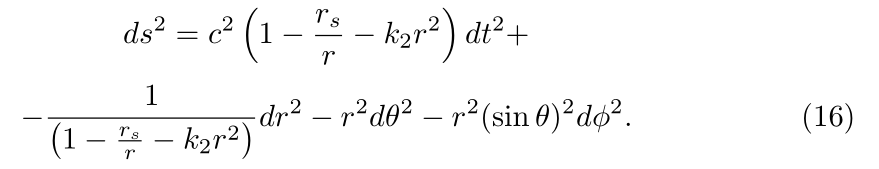
5.1. The Blackhole Horisons
The two horisons are found as
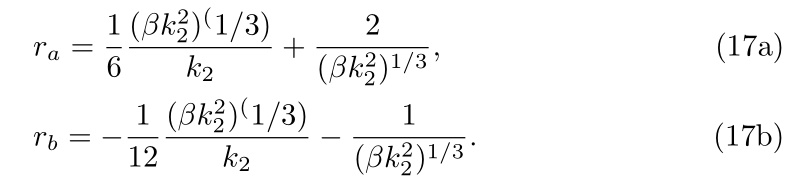
where the functions
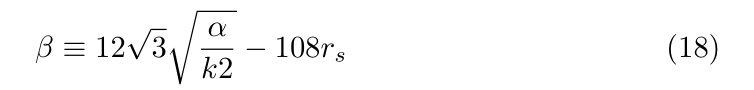
and

are taken. The parametrization is useful to compare the results with those from [4].
The following contrarians are found on the parameter space. The realness of the square root of the function α/k2 is discussed as

from which the result of [4] is refined and extended; in particular, the following new intervals are found.

The denominators of the radii are discussed as

The horison r 2 is identified from the solution of a thrid-degree equation from the condition
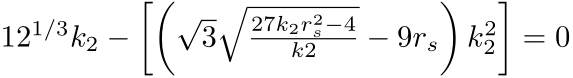
5.2. Coordinate-singularity Avoiding Coordinate Extensions
From the calculations of the orders of the remainders in Equation (10), it is here noticed that the sign of the cosmological constant does not affect the series expansion of the denominator. As a result, the sign of the cosmological constant does not affect the choice of the coordinate-singularity-avoiding coordinates extension. Differently stated, the choice of [11] for a Schwarzschild-deSitter space-time holds also in the case of Schwarzschild-antideSitter spacetimes because also in this case there are no powers with even-denominator exponent of the cosmological-constant term.
6. The Generalized Schwarszchild Spacetimes with a Linear Term
The generalized spherically-symmetric Schwarzschild spacetimes, endowed with a Schwarzschild solid-angle element, are specified after the g tt element

as
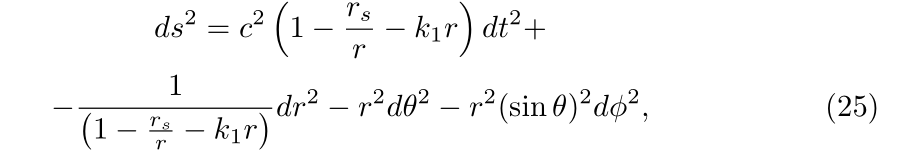
6.1. The Blackhole Horisons
The two horisons are known as
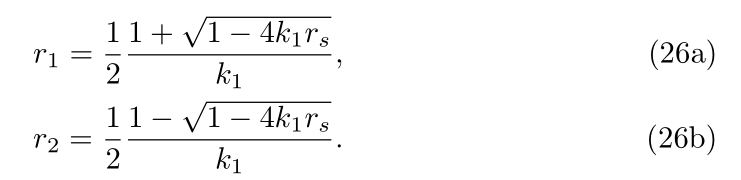
6.2. The Parameter Space
The case of the naked singularity is avoided after avoiding

6.2.1. coordinate-singularity-Avoiding Coordinates Extension
The coordinate-singularity-avoiding coordinate extensions (u,v) are newly found as with new radial coordinate ρ
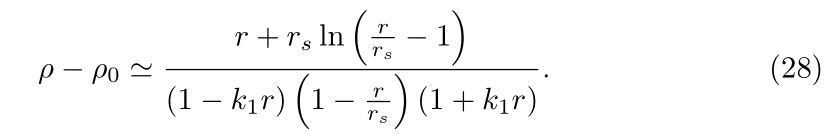
From Equation (28), the initial value of the new radial coordinate ρ is found as

The new expression of T is calculated as

The new further constrain on the linear r from Equation (28) is found as

The coordinate-singularity-avoiding coordinate extensions hold for small modifications of the Schwarzschild radius.
After calculating the zero-th order in r of the coordinates extension, the new condition to characterize the parameter space is obtained

7. Generalized Schwarzschild Spacetimes with a Linear Term and a Cosmological Constant
Generalized spherically-symmetric Schwarzschild spacetimes with a linear term and a cosmological constant are qualified after the g tt element
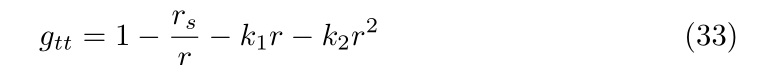
as

7.1. The Blackhole Horisons
The blackhole horisons are written as
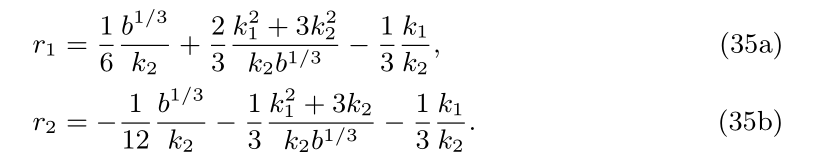
where the function b is taken as
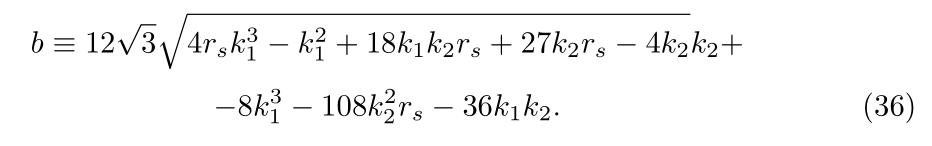
7.2. The Parameter Space
The discussion of the denominator b 6= 0 brings the new constraints on the Schwarzschild radius as
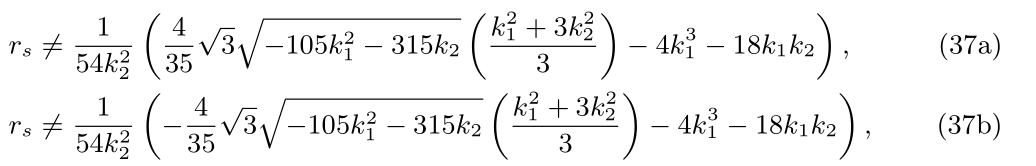
where the new condition on the parameters is requested

The definition of r 2 Equation (35b) defines the new conditions
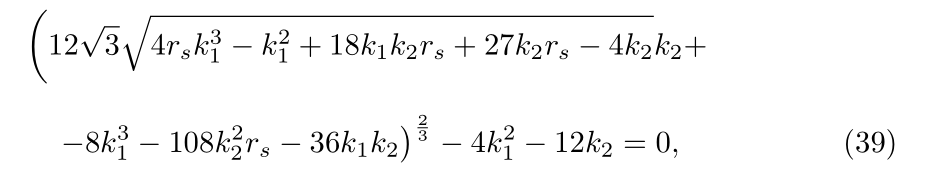
for which the new constraint on the Schwarzschild radius is written
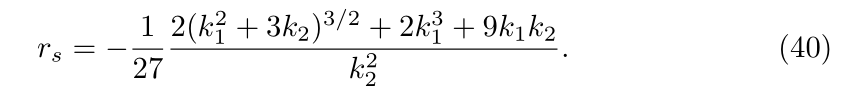
7.3. Coordinate-singularity Avoiding Coordinates Extensions
The coordinate-singularity-avoiding coordinates extensions (u,v) is written after the request that the cosmological-constant term modify the Schwarzschild term only slightly, and that the k 1 term induce a modification of next order; the requests are accomplished after the choice of the new differential
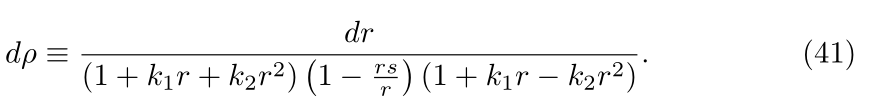
The new radial variable (41) is found as
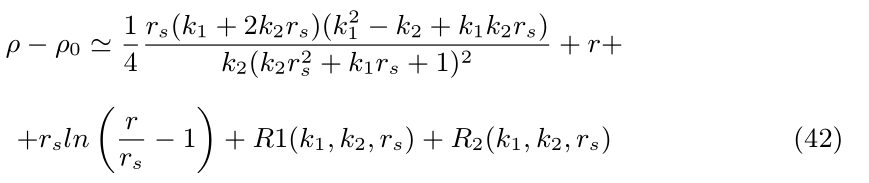
where the initial condition is therefore taken into account. In Equation (42), the remainders of the series expansions are split as R 1 being the remainder of the ln terms containing the contributions to the Schwarzschild radius, and R 2 one related to the contributions due to the parameters k 1 and k 2 . The remainder R 2 matches the conditions from [11]. A new condition is further written

Moreover, the position of the initial value of the new radial variable Equation (42) implies the request

From Equation (41), the new definition of T is found as
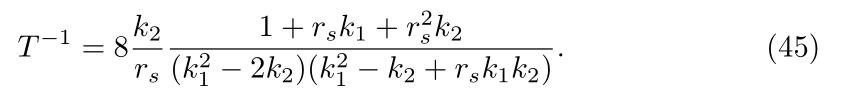
after the new request on the parameter space

8. The Weak-Field Limit
For static spherically-symmetric spacetimes, the weak-field limit (w-fl) is here calculated on the weak-field limit of the Christoffel symbol Γr00 in the linearized
regime.
In the presence of a generalized potential generalized Φ(r) which qualifies the g tt component of the metric tensor as g tt = 1 + φ, one has that Γr00| w−fl =−Φ(r) | w−fl , r . As a result, the Schwarzschild terms lead to the Newtonian potential, the k 2 term is higher orders, while the k 1 term is kept and accounted, i.e., for as helping the galaxy rotation curve.
More specifically, the weak-field limit is considered of the Christoffel symbol from the spherically-symmetric metric

is written as
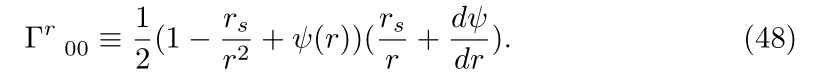
As a result, in the case of the generalized Schwarzschild spacetimes g tt = 1 −rs/r− k 1 r − k 2 r 2 , the Newtonian gravitational potential Φ(r) descends from the r s addends, the non-negligible modification terms descend from the k 1 addends, and the addends containing the k 2 are negligible. The analysis of the addend containing k 21 · k 2 is achieved.
9. Discussion
The protocols implying the presence of the linear term and of the cosmological-constant term can be framed within several analyses, which are all aimed at contributing to constrain and to establish the pertinent possible values of these term for the generalizations of the Schwarzschild spacetime.
As established in [17], the geometrical features of the linear term do not mimic any dark energy component which dynamically interacs with the black hole. The examination of the values allowed for the linear term and for the cosmological- constant term have been scanned from a data-analysis point of view.
The aspects of the terms corresponding to the geometrical mimicking of fluid, which are obtained from the linear-term-related items, have been compared within the experimental viewpoint of COBE-Planck in [18] for the positive value of the cosmological-constant term.
From the observational analyses of CMB, of gravitational waves, of dark matter candidates and of and dark radiation from string cosmology, the potentiality for the scrutinies of the possible values of the linear term and of the cosmological constant were envisaged [19].
Tentative constraints on the values of the (positive) cosmological constant and that of the linear term for a generalized Kottler-Schwarzschild-Kiselev spacetime were presented in [20] from the data analyses.
10. Remarks
The present paper is aimed at the study of the generalized Kottler-Schwarzschild-Kiselev spacetimes, whose g tt component of the metric tensor contains a linear term, a cosmological-constant terms and both the linear term and the cosmological-constant term.
The infinite-redshift surfaces g tt = 0 are written, from whose solution, which constitute the mathematical radii, the physical horizons of the blackhole space-times are originated. The parameter space of the models are set and constrained.
New constraints on the blackhole masses are obtained from the parameter space available for the models.
In the case of the generalized Schwarzschild spacetimes with a cosmological-constant term, both the generalized Schwarzschild-deSitter instance and the generalized Schwarzschild-anti-deSitter instance are examined; the parameter spaces available for the two models are remarkably different.
The coordinate-singularity-avoiding coordinate extensions are provided after [11]; it is here newly examined that the expressions provided with after the generalized Schwarzschild-deSitter spacetimes hold also in the case of the generalized Schwarzschild-anti-deSitter spacetimes, because the corresponding addends in the pertinent series expansions are not affected after the pertinent cosmological-constant sign.
The generalized Schwarzschild spacetimes with a linear term in the g tt component of the metric tensor are scrutinized. The parameter space of the schemes is newly explored. The coordinate-singularity-avoiding coordinate transformations are newly provided with.
The generalized Schwarzschild spacetimes with a linear term and a cosmological-constant term in the g t t component of the metric tensor are studied as well. The physical horizons are newly spelled out.
The coordinate-singularity-avoiding coordinate transformations are newly calculated.
In [21], the cosmological-constant term is written as a function of the innermost-circular-stable-orbit (ISCO) radius and of the linear term; in [22], the ISCO radii of a Kerr spacetime are used for the comparison. It is worth noticing that reverting the equality worked out in [21] implies four determinations of the ISCO radii depending on the cosmological-constant parameter.
References
- Kottler, F. Ueber die physikalischen Grundlagen der Einsteinschen Gravitationstheorie. Ann. Phys. 1918, 56, 401–461.
- Kiselev, V. V. Quintessence and black holes. Class. Quant. Grav. 2003, 20, 1187–1198.
- Lecian, O.M. Generalized Schwarzschild Spacetimes with a Linear Term and a Cosmological Constant. Universe 2024, 10, 408.
- Hayward, S. A.; Nakao K.; Shiromizu, T. A cosmological constant limits the size of black holes. Phys. Rev. D 1994, 49, 5080–5085.
- Lecian, O.M. The Generalised Reissner-Nordstrom Spacetimes, the Cosmological Constant and the Linear Term. Computation 2023, 11, 157.
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 3rd ed.; Pergam Press: Sao Paulo, Brazil,1971.
- Zel’dovich, J.B.; Sunayev, R.A. Astrophysical implications of the neutrino rest mass. I - The universe. Lett. Astron. J. 1980, 6, 451.
- Nariai, H. On some static solutions of Einstein’s gravitational field equa-tions in a spherically symmetric case. Sci. Rep. Tohoku Univ. 1950, 34, 160; Erratm in Ge. Rel. Grav. 1999, 31, 951.
- Nariai, H. On a new cosmological solution of Einstein’s field equations of gravitation. Sci. Rep. Tohoku Univ. 1951, 35, 62; Erratm in Ge. Rel. Grav. 1999, 31, 963.
- Nariai, H. On the Inversion-Invariance of Several Metrics for the Schwarzschild-de Sitter Universe; Research Institute for Theoretical Physics Hiroshima University: Takehara, Hiroshima, 1986; 725, Report number: RRK-86-11.
- Nariai, H. On the Kruskal-Type Representation of Schwarzschild-de Sitter’s Spacetime; Research Institute for Theoretical Physics, Report number: RRK 86-13; Hiroshima University: Takehara, Japan, 1986.
- Gregoris, D.; Ong, Y.C.; Wang, B. A critical assessment of black hole solutions with a linear term in their redshift function. Eur. Phys. J. C 2021, 81, 684–690.
- Wang, L.M.; Caldwell, R.R.; Ostriker, J.P.; Steinhardt, P.J. Cosmic Concordance and Quintessence. Astrophys. J. 2000, 530, 17.
- Chiba, T. Quintessence, the gravitational constant, and gravity. Phys. Rev. D 1999, 60, 083508.
- Bahcall, N.A.; Ostriker, J.P.; Perlmutter, P.J.; Steinhardt, P. The Cosmic Triangle: Revealing the State of the Universe. Science 1999, 284, 1481.
- Steinhardt, P.J.; Wang, L.M.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504.
- Volovich, A.; Gregory, R. Personal Communication; Taylor Francis: London, UK, 2022.
- Sarkar, A.; Ghosh, B. Constraining the quintessential -attractor inflation through dynamical horizon exit method. Phys. Dark Univ. 2023, 41, 101239.
- Cicoli, M.; Conlon, J.P.; Maharana, A.; Parameswaran, S.; Quevedo, F.; Zavala, I. String Cosmology: from the Early Universe to Today; Elsevier: Amsterdam, The Netherlands, 2024.
- Heydari-Fard, M. Effect of Quintessence Dark Energy on the Shadow of Hayward Black Holes with Spherical Accretion; Springer: Berlin/Heidelberg, Germany, 2024.
- Soroushfara; S. Upadhyayb, S. Accretion disks around a static black hole in gravity. Eur. Phys. J. Plus 2020, 135, 338.
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 1972, 178, 347–370.




