You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Angel A. Juan | -- | 1075 | 2024-03-13 08:15:21 | | | |
| 2 | Camila Xu | Meta information modification | 1075 | 2024-03-13 09:42:01 | | | | |
| 3 | Camila Xu | Meta information modification | 1075 | 2024-03-18 08:52:38 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Martin, X.A.; Escoto, M.; Guerrero, A.; Juan, A.A. Different Routing Problems in Transportation. Encyclopedia. Available online: https://encyclopedia.pub/entry/56187 (accessed on 28 December 2025).
Martin XA, Escoto M, Guerrero A, Juan AA. Different Routing Problems in Transportation. Encyclopedia. Available at: https://encyclopedia.pub/entry/56187. Accessed December 28, 2025.
Martin, Xabier A., Marc Escoto, Antoni Guerrero, Angel A. Juan. "Different Routing Problems in Transportation" Encyclopedia, https://encyclopedia.pub/entry/56187 (accessed December 28, 2025).
Martin, X.A., Escoto, M., Guerrero, A., & Juan, A.A. (2024, March 13). Different Routing Problems in Transportation. In Encyclopedia. https://encyclopedia.pub/entry/56187
Martin, Xabier A., et al. "Different Routing Problems in Transportation." Encyclopedia. Web. 13 March, 2024.
Copy Citation
Routing problems refer to a class of optimization problems concerned with finding the most efficient routes or sequences of visits for vehicles tasked with delivering goods or services. These problems typically involve determining optimal paths through a network of nodes (e.g., customers, locations) while satisfying various constraints such as vehicle capacity, time windows, and distance or time limitations.
battery management
electric vehicle routing problems
1. The Vehicle Routing Problem with EVs
Starting with the VRP, this is a well-known challenge that consists in finding optimal routes for a fleet of vehicles, while meeting the demands of customers [1]. Therefore, in VRP problem-solving, the objective is to design routes for cargo vehicles with minimal transportation costs, facilitating the distribution of goods between a central depot and a set of customers. Each customer, assigned to a single product, places demands on the depot, where a fleet of capacitated vehicles (which are typically considered homogeneous) are stationed. These vehicles visit customers to fulfill their demands, eventually returning to the central depot once all customers are served. The optimization goal is minimizing distribution costs, such as travel distance or time-based expenses, to efficiently serve all customers without surpassing the loading capacity of the vehicles. Key constraints include ensuring each route starts and ends at the depot, each customer is visited precisely once by a single vehicle, and the total demand within a route does not exceed the vehicle’s capacity. Figure 1 provides a representation of a simple EVRP scenario, featuring a single depot, multiple customers with specific demands, a homogeneous fleet of EVs with a maximum loading capacity and maximum driving range due to battery constraints, and associated travel costs between any pair of nodes. EVRPs involve planning routes tailored for electric commercial vehicles in the logistics services sector. The fundamental constraints of these EVRPs mainly revolve around managing the variable energy levels upon reaching a customer, initiating routes with a full charge, identifying permissible charging points, and accounting for travel, charging, and service times. To extend the mathematical model of the VRP to the EVRP, new constraints must be incorporated into the original problem. The model is based on the one described by Dantzig and Ramser [2], represented as an undirected graph 𝐺=(𝑉,𝐸). Additional constraints ensure that exactly m vehicles depart from the depot and that each client is visited exactly once. Further constraints are introduced to eliminate sub-tours. To model this problem with EVs, an additional constraint needs to be added to the model. This constraint restricts the total travel distance throughout the tour to the EV’s maximum battery capacity 𝐿ℎ. This constraint can be observed in Equation (1), where 𝑐𝑖𝑗 refers to the battery cost of traveling from node i to node j, and 𝑥ℎ𝑖𝑗 is a binary variable, that takes value 1 if vehicle h traverses the edge (𝑖,𝑗)∈𝐸.
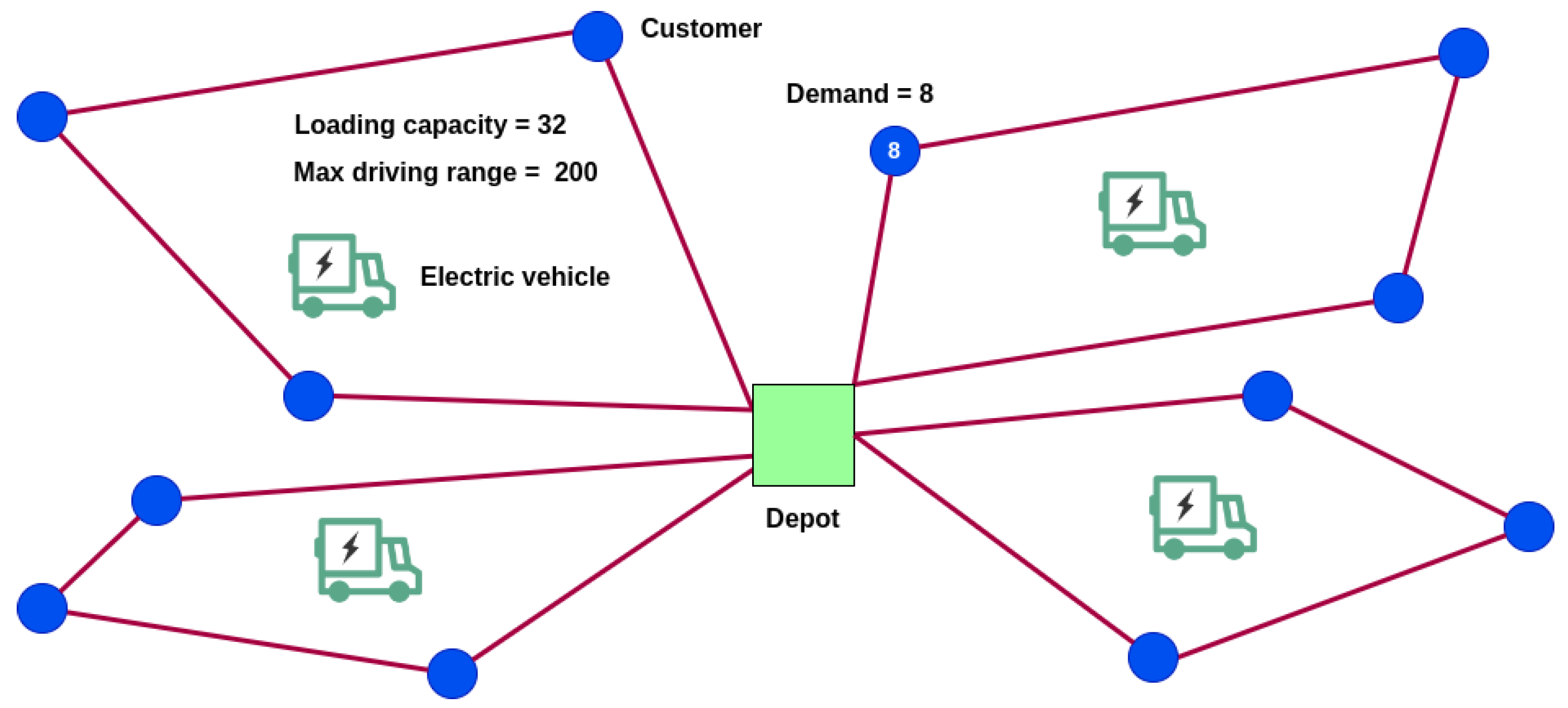
Figure 1. Representation of a simple EVRP.
2. The Team Orienteering Problem with EVs
In contrast to VRPs, where visiting all customers is obligatory, in a TOP the necessity to skip certain customers arises frequently. This is driven by restrictions on fleet size and the maximum allowable route length. Each customer in a typical TOP contributes a reward, collected upon the initial visit. Consequently, solving a TOP involves maximizing the total reward collected by a fixed fleet of vehicles as they visit a set of customers. Unlike the basic version of VRPs, cargo constraints are typically not considered in the basic version of TOPs. When employing EVs, operational constraints stem from their limited driving range. As a consequence, not all customers can be visited, as depicted in Figure 2, which illustrates a basic ETOP. Regarding this problem, a similar process is employed to transform the TOP into an ETOP. The model, based on the one described by Lin [3] incorporates a maximum time per route restriction in addition to the constraints of an EVRP. Contrary to the VRP, the TOP is modeled as a directed graph 𝐺=(𝑁,𝐴), where N stands for the set of nodes and A represents the set of arcs. Given that this maximum time restriction does not need to be related to the vehicle’s maximum traversable distance, the constraint given by Equation (2) needs to be considered.
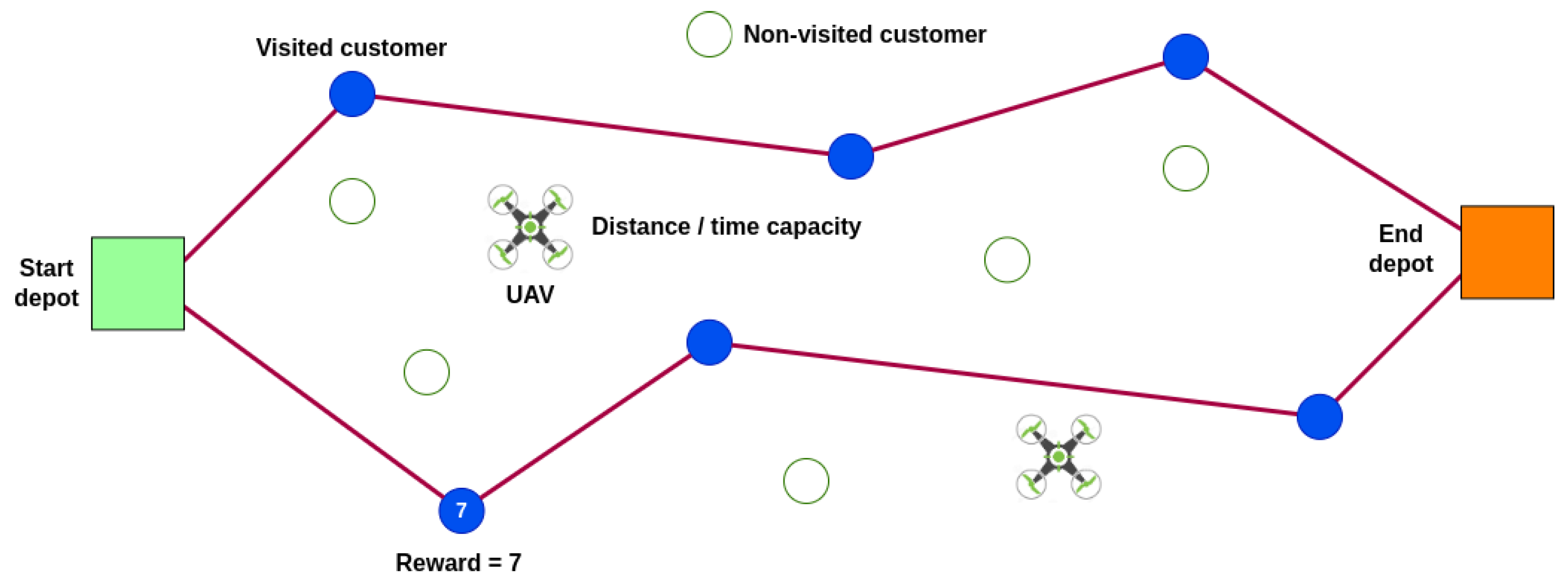
Figure 2. Representation of a basic ETOP.
The integration of unmanned aerial vehicles (UAVs) in cargo transportation by parcel delivery companies has introduced a new dimension to TOP systems. UAVs, constrained by load capacity and battery-driven driving range, pose operational challenges that necessitate careful route planning to avoid failures. Addressing questions of battery recharge locations and timing, a concern not exclusive to UAVs but pertinent to all types of EVs has become a critical aspect of TOP operations [4].
3. The Arc Routing Problem with EVs
The ARP can be modeled on an undirected or a directed graph, where a subset of requesting edges or arcs holds positive demand that requires fulfillment by a fleet of capacitated vehicles, typically treated as homogeneous. The remaining edges, designated as traversing edges, bear null demand. Hence, the visitation of these traversing edges is non-mandatory and they are only used in case they allow a vehicle to visit a requesting edge. In Figure 3, an illustration of a simple EARP is presented. The goal of the EARP lies in finding a set of routes that cover the demands of all requesting edges (arcs), aiming to minimize overall costs. These costs can be delineated in terms of expenditures, traveled distance, or time. Each route is covered by a single capacitated EV, commencing and concluding the journey at a singular depot. The return journey can utilize the same edges (arcs) employed during the outward trip or opt for different ones. It is imperative that the total demand from all requesting edges (arcs) within each route does not surpass the capacity of the assigned vehicle. Furthermore, every edge (arc) with a positive demand must be serviced exactly once. In addition, EVs have to consider a finite driving range, typically quantified in terms of time or distance, which must be adhered to. To transform the ARP into an EARP, whenever this problem is represented with an undirected graph, the constraint given by Equation (1) needs to be added to the problem. Likewise, in the case of a directed graph, the constraint given by Equation (2) would be added. The basic model can be found in Van Bevern et al. [5].

Figure 3. Representation of a simple EARP.
References
- Asghari, M.; Al-e, S.M.J.M. Green vehicle routing problem: A state-of-the-art review. Int. J. Prod. Econ. 2021, 231, 107899.
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91.
- Lin, S.W. Solving the team orienteering problem using effective multi-start simulated annealing. Appl. Soft Comput. 2013, 13, 1064–1073.
- Liao, C.S.; Lu, S.H.; Shen, Z.J.M. The electric vehicle touring problem. Transp. Res. Part Methodol. 2016, 86, 163–180.
- Van Bevern, R.; Hartung, S.; Nichterlein, A.; Sorge, M. Constant-factor approximations for capacitated arc routing without triangle inequality. Oper. Res. Lett. 2014, 42, 290–292.
More
Information
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
681
Revisions:
3 times
(View History)
Update Date:
18 Mar 2024
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




