HTLV-1 Tax Structure Models

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Christophe Guillon	--	1964	2024-03-12 10:06:59	\|
2	Reference format revised.	Lindsay Dong	Meta information modification	1964	2024-03-13 04:21:18	\|

This entry is adapted from the peer-reviewed paper 10.3390/pathogens13030241

Human T-cell Leukemia Virus type 1 (HTLV-1) is a human retrovirus responsible for leukaemia in 5 to 10% of infected individuals. Among the viral proteins, Tax has been described as directly involved in virus-induced leukemogenesis. Tax is therefore an interesting therapeutic target. However, its 3D structure is still unknown and this hampers the development of drug-design-based therapeutic strategies. Several algorithms are available that can be used to predict the structure of proteins, particularly with the recent appearance of artificial intelligence (AI)-driven pipelines. However, Tax seems to be resistant to such predictions.

HTLV-1 Tax structure prediction model zinc finger

1. Introduction

Human T-Leukemia virus type 1 (HTLV-1) was the first oncogenic retrovirus discovered in humans ^[1]. It is estimated that 5 to 10 million people are infected with HTLV worldwide, in areas of high endemicity ^[2]. HTLV is the etiological agent of adult T-cell leukaemia (ATL) and Tropical Spastic Paraparesis (TSP) which occur in 5 to 10% of infected people ^[2]. Interestingly, only HTLV type 1 virus (HTLV-1) but not its type 2 homolog (HTLV-2) induces ATL in humans ^[3]. Among HTLV-1 proteins, Tax plays a central role in viral replication and HTLV-1–related pathologies ^[4]. Tax is a 353-residue-long viral protein (~40 kDa), in which several functional domains have been described ^[5] (Figure 1) which confer numerous functions to the protein.

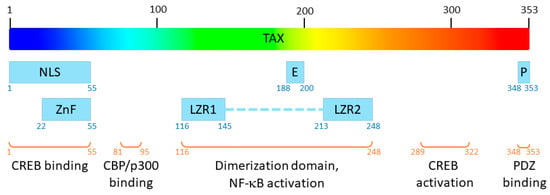
Figure 1. Functional domains of Tax. NLS: nuclear localization signal; E: nuclear export signal, P: PDZ-binding motif; ZnF: zinc finger; LZR1 and LZR2: leucine zipper regions 1 and 2.

Indeed, this viral effector recruits cellular proteins such as RNA polymerase II, CREB transcription factor and p300/CBP coactivator on the viral promotor located in the 5′ LTR of the provirus to allow efficient transcription of the HTLV-1 genome ^[5]^[6]. In addition to its function as a viral transactivator, this pleiotropic oncoprotein is able to interact directly with a large panel of cellular proteins, from transcription factors ^[7]^[8] to proteins involved in cell signalling, cell cycle or apoptotic pathways ^[8]^[9] or mRNA quality control ^[10], thereby playing a central role in HTLV-1 oncogenesis ^[4]^[8]^[11]. In particular, the expression of Tax is necessary for the proliferation of primary T-cells in ATL patients ^[12]. Thus, Tax represents an interesting therapeutic target for treatment against ATL, and deciphering its 3D structure would be a significant breakthrough towards the development of anti-HTLV-1 drugs. Unfortunately, the experimental solving of the 3D structure of Tax remains elusive. To date, the only published structures concerning HTLV-1 Tax are that of short peptides in complex with HLA molecules ^[13]^[14]^[15]^[16]^[17]^[18]^[19]^[20]^[21]^[22]^[23] or structures of the last eight residues of the C-terminal extremity of Tax, forming a PDZ-binding motif, in complex with PDZ proteins ^[24]^[25]^[26]^[27].

In the absence of experimental data on the structure of a complete Tax protein, it is tempting to consider modelling this 3D structure de novo. Until recently, the algorithms for the prediction of protein 3D structures were based on homology modelling: schematically, the algorithm will compare the sequence of the protein of interest (query sequence) with sequences of proteins for which experimental structural data are available in protein structure databases, extract its predicted secondary structures, and compare with those of the sequences of proteins that were the closest homologues in the multiple sequence alignment. Then, based on these sequence/secondary structure alignments, it models the structure of the protein of interest using the 3D scaffold of the identified model(s) and a final energy minimization step. With the emergence of artificial intelligence (AI), new structure prediction pipelines have been described. Schematically, these algorithms are based on neural networks and deep learning that are aggregating the physical and geometric constraints that are present in stretches of sequences present in published protein structures as well as global constraints to generate 3D models. These recent algorithms appear to perform with high efficacy in the yearly critical assessment of protein structure prediction (CASP, https://predictioncenter.org, accessed on 3 February 2024).

2. Predicting the Structure of HTLV-1 Tax

2.1. Predictions Using Homology Modelling

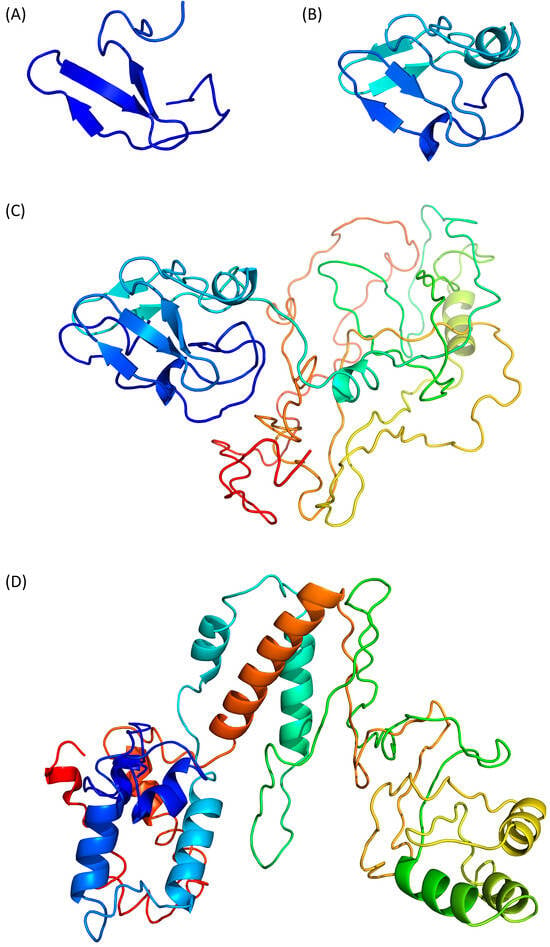
Swiss-Model (https://swissmodel.expasy.org, accessed on 25 January 2024) predicts a β-stranded structure, which includes only 41 residues from the N-terminus of Tax (Figure 2A, residues 27–67). The predicted fragment is homologous to the nitrite reductase small subunit from Vibrio parahaemolyticus (PDB ID 3C0D ^[28]) and its confidence score QMEANDisCo is of 0.31 ± 0.12. Thus, this partial model appears poorly reliable.

Figure 2. Prediction of Tax 3D structure using (A) Swiss-Model, (B) Phyre2 with defaults settings, (C) Phyre2 with “intensive” settings and (D) I-Tasser. Models are coloured from N- to C-terminal from dark blue (residue 1) to red (residue 353), as in Figure 1. Therefore, a single residue will have the same colour on all models, including the partial models (A,B).

Phyre2 (http://www.sbg.bio.ic.ac.uk/phyre2, accessed on 29 January 2024) predicts a structure of a 60 residue-long fragment (Figure 2B, residues 27 to 96), which encompasses the Swiss-Model structure and is homologous to the ferrodoxin component of a bacterial toluene-4-monooxygenase complex (PDB ID 1VM9 ^[29]).

The Phyre2 server can also be used with an “intensive” option to force the modelling of the complete protein through a multiple template modelling (i.e., using several model structures based on local sequence homologies). The predicted region 27–96 is unchanged and the appended modelled parts are constructed from several other template proteins, such as a plant ferrodoxin reductase (PDB ID 1FND ^[30], Tax residues 207–250). The resulting predicted structure is modular with the N- and C-terminal domains separated by a flexible linker (Figure 2C) but the C-terminal part, which is not modelled with the default settings, appears to be loosely folded, with few secondary structure elements.

I-Tasser (https://zhanggroup.org/I-TASSER/, accessed on 26 January 2024) is based on the assembly of PDB templates from local homology domains. The server was able to generate a structure prediction for the full protein (Figure 2D) and the first threading template was the human S-phase kinase-associated protein 2 (PDB ID 1FQV, chain A ^[31]). Because of this new template, the N-terminal domain of Tax is predicted to contain α-helices instead of the previous β-strands. The modelled central region (residues 100–200) and C-terminal extremity (residues 300–353) contains more secondary structure elements than the “Phyre2 intensive” model (Figure 2C,D) but the predicted tertiary structure is still loosely folded. The calculated QMEANDisCo score is also low with a value of 0.35 ± 0.05.

2.2. Predictions Using AI-Based Pipeline

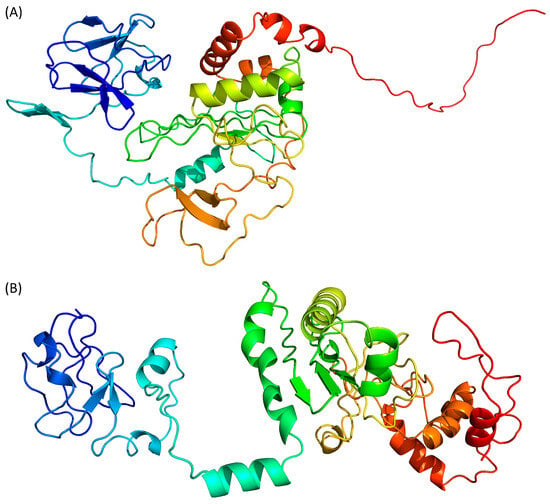
The difficulties in predicting the 3D structure of proteins that have no homologues in structure databases, as described above for Tax, is a problem which has been encountered for years. The recent appearance of AI-based algorithms, which all appeared to perform with high efficacy in international protein structure prediction competitions, has given new hopes for the deciphering ab initio of structure function relationships. Because they are based on different AI-driven processes, there are four of them to predict the structure of Tax: AlphaFold 2 ^[32], RoseTTAFold ^[33], ESMFold ^[34] and D-I-Tasser ^[35] (Figure 3). AlphaFold 2 and ESMFold binaries were installed and run on an in-house server, while RoseTTAFold and D-I-Tasser were run through their primary webservice (https://robetta.bakerlab.org/submit.php accessed on 25 January 2024 and https://zhanggroup.org/D-I-TASSER/ accessed on 26 January 2024, respectively).

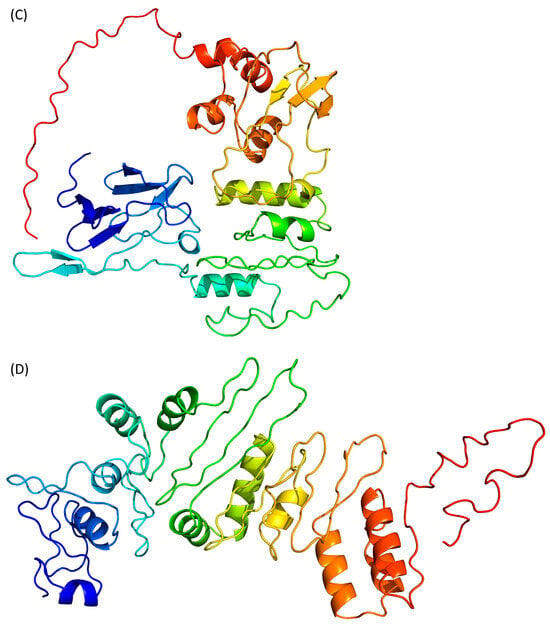
Figure 3. Prediction of Tax 3D structure using (A) AlphaFold 2, (B) RoseTTAFold, (C) ESMFold and (D) D-I-Tasser. Colour scheme is identical to Figure 2.

AlphaFold 2 is using neural networks based on evolutionary, physical and geometric constraints of protein structures ^[32]. The model generated by this algorithm (Figure 3A) shows a two-domains protein. The N-terminal domain is composed of β-strands while the central domain, which is rather compact, contains both β-strands and α-helices.

RoseTTAFold is using a “three-track network” in which information at the sequence, the secondary structure, and the 3D level are successively integrated ^[33]. Based on the Tax sequence, RoseTTAFold is also predicting a two-domain protein, separated by an isolated α-helix (Figure 3B). Both the N- and C-terminal domains are containing a mixture of β-strands and α-helices. However, by opposition to the AlphaFold 2 model, the C-terminal region of Tax is predicted here as containing two α-helices. The N-terminal region (residues 20–74) is predicted to contain helical motifs that are absent from the AlphaFold 2 model (Figure 3A).

ESMFold adopts a different approach, as it uses language models trained on protein sequences and therefore does not depend on multiple sequence alignments ^[34]. ESMFold, like the other AI-based algorithms, predicts that the Tax protein is composed of two domains (Figure 3C).

Finally, scholars used D-I-Tasser which is an evolution of I-Tasser (see above) that includes a deep neural-network predictors analysis coupled to the I-Tasser force fields (Figure 3D). D-I-Tasser predicted a model for the whole protein and the first threading template is, this time, a protein from the drosophila apoptosome (PDB ID 1VT4 ^[36]). As a consequence, the predicted topology is different from the I-Tasser one and the D-I-Tasser model has more α-helices (Figure 2D and Figure 3D).

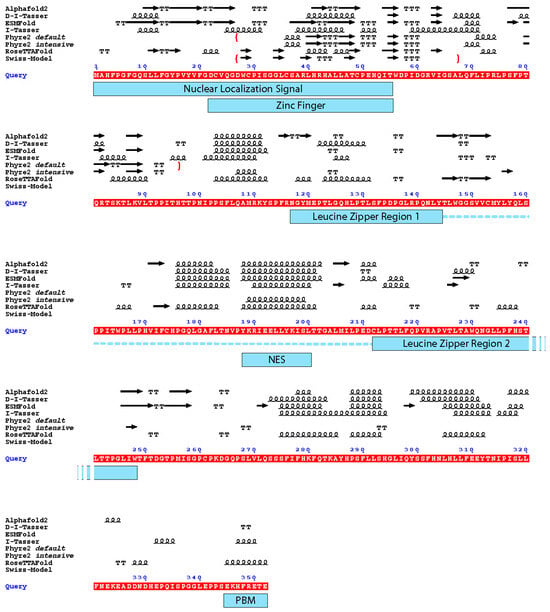
3. Comparison of HTLV-1 Tax Structure Models

Two of the four AI-generated models (RoseTTAFold and ESMFold) exhibited the best local confidence scores for the N-terminal domain of Tax, which is the zinc finger domain which was also modelled by Swiss-Model and Phyre2. Thus, scholars compared the secondary structures elements of all these models with respect to Tax functional regions (Figure 4).

Figure 4. Depiction of the secondary structure elements from the different models with the functional domains of the Tax protein. Underlined in red is the sequence of Tax used for the modelling (Query). Above the sequence: arrow: β-strand. Squiggles: α-helix. T: turn. The boundaries of the partial models are depicted by red brackets. Under the sequence, blue rectangles mark the functional domains of Tax depicted in Figure 1; the dotted line together with the leucine zipper regions depict the dimerization domain of Tax. NES: Nuclear Export Signal; PBM: PDZ-binding motif. The figure was generated by ESPript 3.0 ^[37].

It appears that the Nuclear Export Signal and the centre of the dimerization domain are predicted as being in an α-helical region by all predictors that modelled this region (residues 175–205). Notably, it is the region which had the best local confidence score in the D-I-Tasser model. For the rest of the protein, none of the models are convergent (Figure 4).

As there are a lot of different topologies for zinc fingers that have already been described in the literature ^[37], this observation could suggest that the Tax protein harbours another, yet undescribed, zinc finger topology that the algorithms do not identify, especially as they do not support the prediction of metal coordination. Indeed, although not superposing, both ESMFold and RoseTTAFold predicted three cysteines (C29, C36 and C49) and one histidine (H52) in close vicinity, which could coordinate a zinc ion. Such zinc fingers with three cysteines and one histidine (CCCH) have been described and are involved in RNA metabolism ^[38]. Their consensus sequence is C-(X_4–15)-C-(X_4–6)-C-(X_3–4)-H (with X for any amino-acid) ^[39]. Thus, this putative CCCH zinc finger in Tax, with the sequence C-X₆-C-X₁₂-C-X₂-H, would be non-canonical and marked by a particularly longer distance between the second and third cysteines (12 instead of 4 to 6). Of note, this zinc finger is also predicted by AlphaFold 2 but not by D-I-Tasser, nor by any other homology modelling method.

Another possibility is that this region of Tax is intrinsically disordered and that the zinc finger is only forming through induced folding when Tax interacts with a biological partner. The formation of the zinc finger of Tax could also require trans-complementation with domains or residues of the interacting partner, as it contains only seven cysteines or histidine residues while eight are needed to complete two zinc fingers. Such an induced folding and trans-complementation for the formation of the zinc finger have been described for the HIV-1 Tat protein: this regulatory protein, which is intrinsically disordered ^[40]^[41], contains seven cysteine residues and uses a residue from its interacting partner, Cyclin T1, to complete its two zinc fingers that are then folded as α-helices ^[42].

A third possibility comes from the fact that Tax can undergo several post-translational modifications, such as phosphorylation, acetylation, SUMOylation and/or poly-ubiquitination which are important for its function ^[1] and may influence its conformation. However, there is no algorithm to date which includes this parameter during protein structure prediction

References

Poiesz, B.J.; Ruscetti, F.W.; Gazdar, A.F.; Bunn, P.A.; Minna, J.D.; Gallo, R.C. Detection and isolation of type C retrovirus particles from fresh and cultured lymphocytes of a patient with cutaneous T-cell lymphoma. Proc. Natl. Acad. Sci. USA 1980, 77, 7415–7419.
Gessain, A.; Cassar, O. Epidemiological aspects and world distribution of HTLV-1 infection. Front. Microbiol. 2012, 3, 388.
Martinez, M.P.; Al-Saleem, J.; Green, P.L. Comparative virology of HTLV-1 and HTLV-2. Retrovirology 2019, 16, 21.
Currer, R.; van Duyne, R.; Jaworski, E.; Guendel, I.; Sampey, G.; Das, R.; Narayanan, A.; Kashanchi, F. HTLV tax: A fascinating multifunctional co-regulator of viral and cellular pathways. Front. Microbiol. 2012, 3, 406.
Boxus, M.; Twizere, J.-C.; Legros, S.; Dewulf, J.-F.; Kettmann, R.; Willems, L. The HTLV-1 Tax interactome. Retrovirology 2008, 5, 76.
Martella, C.; Waast, L.; Pique, C. Tax, marionnettiste de la transcription du HTLV-1. Med. Sci. 2022, 38, 359–365.
Fochi, S.; Mutascio, S.; Bertazzoni, U.; Zipeto, D.; Romanelli, M.G. HTLV deregulation of the NF-kappaB pathway: An update on Tax and antisense proteins role. Front. Microbiol. 2018, 9, 285.
Mohanty, S.; Harhaj, E.W. Mechanisms of Oncogenesis by HTLV-1 Tax. Pathogens 2020, 9, 543.
Simonis, N.; Rual, J.-F.; Lemmens, I.; Boxus, M.; Hirozane-Kihijawa, T.; Gatot, J.-S.; Dricot, A.; Hao, T.; Vertommen, D.; Legros, S.; et al. Host-pathogen interactome mapping for HTLV-1 and HTLV-2. Retrovirology 2012, 9, 26.
Fiorini, F.; Robin, J.P.; Kanaan, J.; Borowiak, M.; Croquette, V.; Le Hir, H.; Jalinot, P.; Mocquet, V. HTLV-1 Tax plugs and freezes UPF1 helicase leading to nonsense-mediated mRNA decay inhibition. Nat. Commun. 2018, 9, 431.
Higuchi, M.; Fujii, M. Distinct functions of HTLV-1 Tax1 from HTLV-2 Tax2 contribute key roles to viral pathogenesis. Retrovirology 2009, 6, 117.
Hleihel, R.; Skayneh, H.; de The, H.; Hermine, O.; Bazarbachi, A. Primary cells from patients with adult T cell leukemia/lymphoma depend on HTLV-1 Tax expression for NF-kappaB activation and survival. Blood Cancer J. 2023, 13, 67.
Garboczi, D.N.; Ghosh, P.; Utz, U.; Fan, Q.R.; Biddison, W.E.; Wiley, D.C. Structure of the complex between human T-cell receptor, viral peptide and HLA-A2. Nature 1996, 384, 134–141.
Gagnon, S.J.; Borbulevych, O.Y.; Davis-Harrison, R.L.; Baxter, T.K.; Clemens, J.R.; Armstrong, K.M.; Turner, R.V.; Damirjian, M.; Biddison, W.E.; Baker, B.M. Unraveling a hotspot for TCR recognition on HLA-A2: Evidence against the existence of peptide-independent TCR binding determinants. J. Mol. Biol. 2005, 353, 556–573.
Ding, Y.H.; Smith, K.J.; Garboczi, D.N.; Utz, U.; Biddison, W.E.; Wiley, D.C. Two human T cell receptors bind in a similar diagonal mode to the HLA-A2/Tax peptide complex using different TCR amino acids. Immunity 1998, 8, 403–411.
Ding, Y.H.; Baker, B.M.; Garboczi, D.N.; Biddison, W.E.; Wiley, D.C. Four A6-TCR/peptide/HLA-A2 structures that generate very different T cell signals are nearly identical. Immunity 1999, 11, 45–56.
Gagnon, S.J.; Borbulevych, O.Y.; Davis-Harrison, R.L.; Turner, R.V.; Damirjian, M.; Wojnarowicz, A.; Biddison, W.E.; Baker, B.M. T cell receptor recognition via cooperative conformational plasticity. J. Mol. Biol. 2006, 363, 228–243.
Piepenbrink, K.H.; Borbulevych, O.Y.; Sommese, R.F.; Clemens, J.; Armstrong, K.M.; Desmond, C.; Do, P.; Baker, B.M. Fluorine substitutions in an antigenic peptide selectively modulate T-cell receptor binding in a minimally perturbing manner. Biochem. J. 2009, 423, 353–361.
Khan, A.R.; Baker, B.M.; Ghosh, P.; Biddison, W.E.; Wiley, D.C. The structure and stability of an HLA-A*0201/octameric tax peptide complex with an empty conserved peptide-N-terminal binding site. J. Immunol. 2000, 164, 6398–6405.
Singh, N.K.; Alonso, J.A.; Harris, D.T.; Anderson, S.D.; Ma, J.; Hellman, L.M.; Rosenberg, A.M.; Kolawole, E.M.; Evavold, B.D.; Kranz, D.M.; et al. An Engineered T Cell Receptor Variant Realizes the Limits of Functional Binding Modes. Biochemistry 2020, 59, 4163–4175.
Borbulevych, O.Y.; Piepenbrink, K.H.; Gloor, B.E.; Scott, D.R.; Sommese, R.F.; Cole, D.K.; Sewell, A.K.; Baker, B.M. T cell receptor cross-reactivity directed by antigen-dependent tuning of peptide-MHC molecular flexibility. Immunity 2009, 31, 885–896.
Li, L.; Muzahim, Y.; Bouvier, M. Crystal structure of adenovirus E3-19K bound to HLA-A2 reveals mechanism for immunomodulation. Nat. Struct. Mol. Biol. 2012, 19, 1176–1181.
Madden, D.R.; Garboczi, D.N.; Wiley, D.C. The antigenic identity of peptide-MHC complexes: A comparison of the conformations of five viral peptides presented by HLA-A2. Cell 1993, 75, 693–708.
Gogl, G.; Zambo, B.; Kostmann, C.; Cousido-Siah, A.; Morlet, B.; Durbesson, F.; Negroni, L.; Eberling, P.; Jane, P.; Nomine, Y.; et al. Quantitative fragmentomics allow affinity mapping of interactomes. Nat. Commun. 2022, 13, 5472.
Maseko, S.B.; Brammerloo, Y.; van Molle, I.; Sogues, A.; Martin, C.; Gorgulla, C.; Plant, E.; Olivet, J.; Blavier, J.; Ntombela, T.; et al. Identification of small molecule antivirals against HTLV-1 by targeting the hDLG1-Tax-1 protein-protein interaction. Antiviral Res. 2023, 217, 105675.
Cousido-Siah, A.; Carneiro, L.; Kostmann, C.; Ecsedi, P.; Nyitray, L.; Trave, G.; Gogl, G. A scalable strategy to solve structures of PDZ domains and their complexes. Acta Crystallogr. D Struct. Biol. 2022, 78, 509–516.
Javorsky, A.; Maddumage, J.C.; Mackie, E.R.R.; Soares da Costa, T.P.; Humbert, P.O.; Kvansakul, M. Structural insight into the Scribble PDZ domains interaction with the oncogenic Human T-cell lymphotrophic virus-1 (HTLV-1) Tax1 PBM. FEBS J. 2023, 290, 974–987.
Kuzin, A.P.; Abashidze, M.; Seetharaman, J.; Vorobiev, S.M.; Wang, D.; Fang, Y.; Owens, L.; Ma, L.-C.; Xiao, R.; Liu, J.; et al. Crystal Structure of the Putative Nitrite Reductase NADPH (Small Subunit) Oxidoreductase Protein Q87HB1. Available online: https://www.wwpdb.org/pdb?id=pdb_00003c0d (accessed on 3 February 2024).
Moe, L.A.; Bingman, C.A.; Wesenberg, G.E.; Phillips, G.N., Jr.; Fox, B.G. Structure of T4moC, the Rieske-type ferredoxin component of toluene 4-monooxygenase. Acta Crystallogr. D Biol. Crystallogr. 2006, 62, 476–482.
Bruns, C.M.; Karplus, P.A. Refined crystal structure of spinach ferredoxin reductase at 1.7 A resolution: Oxidized, reduced and 2′-phospho-5′-AMP bound states. J. Mol. Biol. 1995, 247, 125–145.
Schulman, B.A.; Carrano, A.C.; Jeffrey, P.D.; Bowen, Z.; Kinnucan, E.R.; Finnin, M.S.; Elledge, S.J.; Harper, J.W.; Pagano, M.; Pavletich, N.P. Insights into SCF ubiquitin ligases from the structure of the Skp1-Skp2 complex. Nature 2000, 408, 381–386.
Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Zidek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589.
Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876.
Lin, Z.; Akin, H.; Rao, R.; Hie, B.; Zhu, Z.; Lu, W.; Smetanin, N.; Verkuil, R.; Kabeli, O.; Shmueli, Y.; et al. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science 2023, 379, 1123–1130.
Zheng, W.; Wuyun, Q.; Freddolino, P.L.; Zhang, Y. Integrating deep learning, threading alignments, and a multi-MSA strategy for high-quality protein monomer and complex structure prediction in CASP15. Proteins 2023, 91, 1684–1703.
Yuan, S.; Yu, X.; Topf, M.; Dorstyn, L.; Kumar, S.; Ludtke, S.J.; Akey, C.W. Structure of the Drosophila apoptosome at 6.9 a resolution. Structure 2011, 19, 128–140.
Kluska, K.; Adamczyk, J.; Krezel, A. Metal binding properties of zinc fingers with a naturally altered metal binding site. Metallomics 2018, 10, 248–263.
Hajikhezri, Z.; Darweesh, M.; Akusjarvi, G.; Punga, T. Role of CCCH-Type Zinc Finger Proteins in Human Adenovirus Infections. Viruses 2020, 12, 1322.
Yuan, S.; Xu, B.; Zhang, J.; Xie, Z.; Cheng, Q.; Yang, Z.; Cai, Q.; Huang, B. Comprehensive analysis of CCCH-type zinc finger family genes facilitates functional gene discovery and reflects recent allopolyploidization event in tetraploid switchgrass. BMC Genom. 2015, 16, 129.
Foucault, M.; Mayol, K.; Receveur-Bréchot, V.; Bussat, M.-C.; Klinguer-Hamour, C.; Verrier, B.; Beck, A.; Haser, R.; Gouet, P.; Guillon, C. UV and X-ray structural studies of a 101-residue long Tat protein from a HIV-1 primary isolate and of its mutated, detoxified, vaccine candidate. Proteins 2010, 78, 1441–1456.
Shojania, S.; O’Neil, J.D. HIV-1 Tat is a natively unfolded protein: The solution conformation and dynamics of reduced HIV-1 Tat-(1-72) by NMR spectroscopy. J. Biol. Chem. 2006, 281, 8347–8356.
Tahirov, T.H.; Babayeva, N.D.; Varzavand, K.; Cooper, J.J.; Sedore, S.C.; Price, D.H. Crystal structure of HIV-1 Tat complexed with human P-TEFb. Nature 2010, 465, 747–751.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Virology

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Christophe Guillon

Xavier Robert

Patrice Gouet

View Times: 55

Update Date: 13 Mar 2024

Table of Contents

Video Upload Options

Confirm