Lifetime Assessment Models for Coastal Reinforced Concrete Structures

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Luis F. Rincon	--	2281	2024-02-28 11:48:34	\|
2	format	Jason Zhu	Meta information modification	2281	2024-02-29 02:13:51	\| \|
3	format	Jason Zhu	-22 word(s)	2259	2024-03-01 11:25:21	\|

This entry is adapted from the peer-reviewed paper 10.3390/buildings14030562

Modern engineering faces challenges in ensuring technical standards for service, durability, and sustainability. Political, administrative, and budgetary factors, coupled with climate change, pose tasks to structural integrity, affecting industries and economies. Marine infrastructures represent a strategic asset of a country as they handle a large part of the economic exchanges.

chloride-induced corrosion reinforcement concrete degradation models

1. Introduction

Establishing maintenance schedules that preserve and/or extend the structures’ lifespans considering environmental, social, and economic impact is essential for modern society. In this field, degradation models contribute to understanding the deterioration process and determining the long-term performance of the asset. Therefore, they are essential in defining the type and timing of maintenance actions, which is crucial for ensuring that the system operates well.

This topic review presents the main research in this field applied especially to the corrosion propagation phase, where the corrosion produces a cross-sectional reduction in the reinforcement and an accumulation of corrosion products at the interface between concrete and steel, which leads to tensile stresses that initiate cracks, delamination, and spalling of concrete cover ^[1].

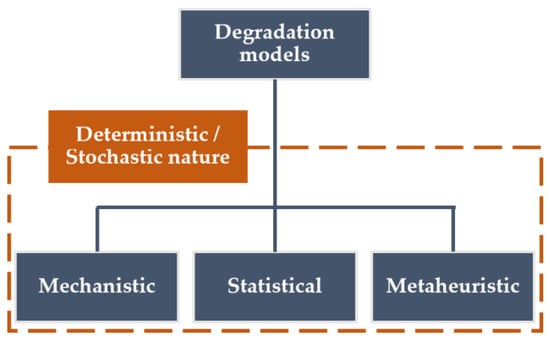
Once corrosion produces visible signs of deterioration, some degradation models make use of visual inspections to determine the future deterioration of the element or structure. Other degradation models focus on specific deterioration phenomena, such as corrosion, and consider the propagation phase, or even the initiation phase. Therefore, the nature of the degradation models can be deterministic or stochastic. In this context, the models published to date can be separated into three categories, as shown in Figure 1.

Figure 1. Main categories of degradation models. Adapted from ^[2]^[3].

2. Mechanistic Models

Mechanistic models aim to establish the relationship between the variables that influence the phenomenon and the observed outcomes. In general, mechanistic models are based on parameters with a high impact on the structural capacity and reliability such as material properties or stress conditions ^[3].

Villain et al. ^[4] developed a 3D cross-correlation model to perform a durability diagnosis to analyze a wharf of the Nantes–Saint-Nazaire Port, using laboratory tests and non-destructive techniques. Ožbolt et al. ^[5] present a three-dimensional fully coupled chemo–hygro–thermo–mechanical model to simulate the effects of corrosion of steel in concrete and evaluate the damage to the structure. More recently, Bui and Tan ^[6] presented a finite element model to simulate nonuniform corrosion-induced concrete cracking considering microcell and microcell mechanisms to determine the total corrosion rate. The results evidence that vertical cracks accelerated the spread of the corroded area and created a more rounded corrode depth.

A similar study was presented by Nguyen et al. ^[7], who predicted the chloride’s penetration into the concrete using a coupled thermo–hydro–chemical model but went beyond by considering multiple factors affecting the phenomena including diffusion, convection, chloride binding, ionic interaction, and concrete aging. Additionally, the researchers proposed a model simplification to reduce the computational cost, proving it to be efficient and accurate for long-term chloride ingress modeling and reducing the need for larger climate databases. In general, mechanistic models provide a reliable lifetime assessment. However, the main disadvantage of their implementation is the high cost in terms of data requirement and modeling, making it inefficient on a wider scale.

3. Statistical Models

Statistical models are based on the interpretation of a database of existing knowledge of failures or historical data to estimate future deteriorations. These models are often used for estimating the long-term performance of structures like bridges and are based on deterministic or stochastic approaches.

Markov Chain (MC) models stand out in this section because they are based on the discretization of the condition of the structural elements or systems and estimate a probability that the analyzed element deteriorates to the following state in a period ^[8]. Figure 2 presents a schematic of the transition of the degradation process of RC structures according to MC models, including the appearance and propagation of cracking and spalling. These probabilities can be established from expert opinions and/or monitoring data available ^[9].

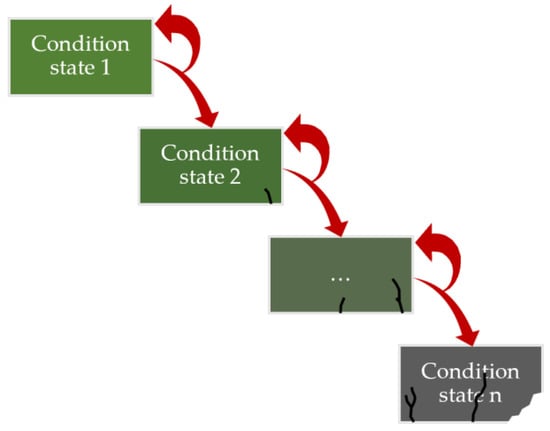
Figure 2. Transition of the degradation process according to MC models.

MC models have been applied to different types of structures and materials ^[10]^[11]^[12]^[13]^[14]. Considering the marine environment, Bastidas-Arteaga and Schoefs ^[15] presented a methodology that combines a numerical model of chloride penetration, the Markov degradation process, and decision theory. The research is based on the discussion with stakeholders on the integration of inspection data and chloride penetration models; however, further research is needed on the factors influencing the corrosion initiation such as environmental aspects and characteristics of the concrete and repair material.

A similar work was presented by Zhang et al. ^[16], where a structural degradation model was developed for a wharf in Tokyo. The formulation was based on a randomized MC model to describe the port infrastructural deteriorations and works as a more flexible tool to quantify the uncertainties associated with the deterioration process, compared to a deterministic approach.

3.1. Probabilistic Models

Probabilistic models take into account the variability of the different components of the phenomenon and establish that a deterministic analysis may provide more inaccurate results. Kwon et al. ^[17] used field data from two wharves of 8 and 11 years of service in South Korea for the probabilistic prediction of the service life of RC structures exposed to the marine environment conditions considering the crack effect on chloride penetration through the relationship between diffusion coefficients and crack widths. The results predict a shorter service life than that calculated using deterministic methods.

Bastidas-Arteaga et al. ^[18] developed a probabilistic lifetime prediction model for RC structures under the coupled effect of corrosion and fatigue, and the results show that the coupled effect strongly affects performance, leading to a large reduction in the expected lifespan. Imounga et al. ^[1] analyzed a similar situation, where they considered the effects of chloride-induced corrosion and load-induced concrete cracking on the serviceability and safety of RC structures.

Bastidas-Arteaga et al. ^[19] presented a stochastic model that considered the effects of convection, chloride binding, concrete aging, temperature, and humidity to study the influence of weather conditions and global warming on chloride ingress and the evaluation of the corrosion initiation time. The results show a lifetime reduction ranging from 2 to 18% on RC structures located in oceanic environments due to climate change and the importance of the implementation of countermeasures directed to reduce and/or mitigate the action of global warming on weather and minimize the impact of climate change on RC structures.

Molyneaux et al. ^[20] developed a probabilistic model for the deterioration of RC elements of Australian port infrastructures due to corrosion, cracking, and spalling. The study performed a parametric analysis of the influence of the variation in the concrete cover, the surface chloride concentration, and the diffusion coefficient, finding in the latter the largest variation observed in the field and its high sensitivity in the model. The model estimates the onset of corrosion of the analyzed elements, assuming a normal distribution of the input variables. Later, Homer, Law, and Molyneaux ^[21] extended the study by analyzing the statistical distribution of specified cover, element type, and method of construction.

Other studies such as ^[22] have developed a model to predict the service life of high-pile wharf structures in China by considering a probabilistic model for surface chloride content and chloride diffusion. The research was based on exposure trials and field data of seventeen high-pile wharf structures located on the south coast of China and presented reasonable results for concrete in the splash zone but significantly smaller chloride content results for the semi-splash zone.

Yu et al. ^[23] developed a time-dependent probabilistic model to describe chloride ingress for the durability assessment of RC structures. The model with a reliability index is highly dependent on characteristics such as the apparent chloride diffusion coefficient, the water-to-cement ratio, curing periods, and the depth of concrete cover. This model is less reliable for tidal zones than for splash and submerged zones.

Pereira et al. ^[24] used data from a 50-year-old bridge on a port in Portugal to establish structure deterioration models with a deterministic nature, based on the Model Code 2010 and the E465 specification from the Portuguese National Laboratory for Civil Engineering (LNEC). The results show that these models are too conservative and alluded to information not considered for the models such as cracks in the structure.

More recently, Pang et al. ^[25] analyzed the relationship between flexural strength, temperature, relative humidity, geometric parameters, and corrosion probability. The results showed high variability in corrosion probabilities depending on the exposure zone. The authors remarked that the randomness of temperature and humidity should be considered in the analysis of chloride ingress for RC beams on offshore atmospheric zones.

Due to the high uncertainty of the main factors influencing corrosion deterioration of coastal structures, a large number of models have been proposed. These models vary in complexity and applicability and have been implemented locally, so their adaptability to different climatic conditions has not been studied extensively. Statistical models in general have great advantages such as their simple approach and practicality at a network level. However, they ignore the interaction between degradation and the different components of the structures. Additionally, they provide qualitative results due to their basis on qualitative damage scales; therefore, the safety and reliability of the structure in terms of resistance are questionable ^[3]. Finally, the outputs of the models depend strongly on the information available. Models like the one by Mauch and Madanat ^[26] need at least 20 years of data; therefore, there are only specific cases where they can be applied.

4. Metaheuristic Models for Prediction

Metaheuristic algorithms are gradient-free, iterative, and frequently population-based approaches that start with a set of initial random solutions ^[27]. These models use searching tactics, such as exploration and exploitation, to steadily enhance the quality of solutions. They are specially designed to solve highly complex Nondeterministic Polynomial (NP) hard problems and have been applied for the solution for a variety of engineering problems.

Metaheuristic models include:

Expectation-maximization (EM) approach ^[28];
Case-Based Reasoning (CBR) ^[29];
Evolutionary algorithms like genetic algorithms ^[30];
Shuffled frog leaping ^[31];
Particle swarm optimization ^[32];
Artificial Neural Network (ANN) algorithms.

Among these, ANNs have become popular as they overcome the deficiencies of current mechanistic, probabilistic, and statistical models in degradation prediction. The ANN concept is an artificial intelligence method which is originated from the human brain’s understanding ^[33]. It consists of each neuron processing information separately and simultaneously, mimicking the brain’s functioning. ANNs obtain knowledge through the training phase, which is established by using a set of training data, where the system identifies the relationship between the input and output parameters. The concept of synaptic weights is determined to store the knowledge from training and to use it to solve problems for an unknown dataset ^[34]. Figure 3 presents an example of a neural network.

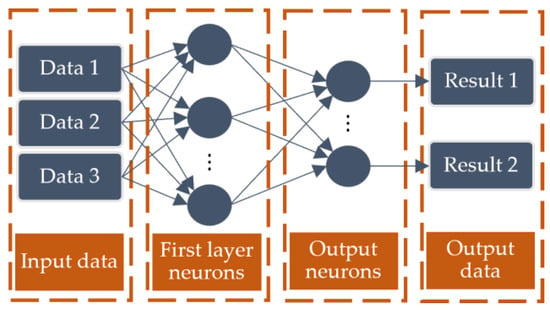
Figure 3. Example of a neural network. Adapted from ^[35].

In the context of coastal infrastructure, Ukrainczyk, Banjad, and Ukrainczyk ^[36] applied an ANN in the prediction of the expected future degree of damage considering a damage classification of steel corrosion gathered in three concrete structures in a marine environment, two bridges and a torpedo factory in Croatia. The authors classified the damage caused by corrosion into five categories, which corresponded to the types of work that would be required to repair the damage and corresponded to information obtained by testing and visual inspections. The results show that the ANN model developed can predict damage degree accurately and was able to analyze the influence of the main parameters on the damage. However, the model depends on the available data, so its reliability in predicting damage may vary depending on the structure and historical data.

Asghshahr, Rahai, and Ashrafi ^[37] used laboratory data on chloride penetration to develop classification and regression trees (CARTs) and ANN models to predict chloride concentration considering environmental conditions, penetration depth, water-to-cementitious material ratio, and silica fume mass as input parameters. The results showed a good ability and accuracy of the models for predicting the chloride concentration in concrete under marine environment conditions, with the best accuracy shown by the ANN model.

Lyne C and Lejano ^[38], presented an ANN model for estimating the microcell current density of steel in mortar mixed with seawater, where several variables were considered as input variables and the results consisted of eight input variables, eight neurons in the hidden layer, and one output variable. The resulting neural network model satisfactorily predicted the corrosion current density with high correlation coefficients. Other studies, such as ^[39], evaluated five metaheuristic models in the prediction of pitting corrosion risk and marine corrosion rate. The results were compared with two real-world datasets and a hybrid model combining support vector regression (SVR) with a smart nature-inspired metaheuristic optimization algorithm and presented the lowest errors.

More recently, Mohammadi et al. ^[40] proposed the use of an ANN optimized by four marine creature-based metaheuristic algorithms to model the apparent chloride diffusion of concrete exposed to atmosphere, tidal, splash, and submerged environments. The models were evaluated with 216 data points from relevant field experiments from the literature and the Wilcoxon rank-sum test showed that the ANN-JSO (Jellyfish Search Optimizer) algorithm showed better results. In the same year, Rincon et al. ^[41] developed MC models and ANN models to describe the degradation process of a marine exposed and repaired structure using data from corrosion sensors from 2006 to 2020. The results demonstrated the potential applicability of these models due to the lower errors obtained.

Therefore, it is possible to say that metaheuristic models could capture complex phenomena without prior knowledge. Within the metaheuristic models, ANN models are highlighted due to the possibility of generating estimations with higher accuracy. Additionally, ANN-based techniques can generate missing data to fill gaps. However, there are some disadvantages, such as a lack of transparency in their decision-making process and the high inaccuracy of the results when sufficient data are not available.

References

Imounga, H.M.; Bastidas-Arteaga, E.; Moutou Pitti, R.; Ekomy Ango, S.; Wang, X.-H. Bayesian Assessment of the Effects of Cyclic Loads on the Chloride Ingress Process into Reinforced Concrete. Appl. Sci. 2020, 10, 2040.
Falamarzi, A.; Moridpour, S.; Nazem, M. A Review of Rail Track Degradation Prediction Models. Aust. J. Civ. Eng. 2019, 17, 152–166.
Srikanth, I.; Arockiasamy, M. Deterioration Models for Prediction of Remaining Useful Life of Timber and Concrete Bridges: A Review. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 152–173.
Villain, G.; Sbartaï, Z.M.; Dérobert, X.; Garnier, V.; Balayssac, J.-P. Durability Diagnosis of a Concrete Structure in a Tidal Zone by Combining NDT Methods: Laboratory Tests and Case Study. Constr. Build. Mater. 2012, 37, 893–903.
Ožbolt, J.; Kušter, M.; Balabanić, G.; Oršanić, F. Numerical Modelling of Degradation of Reinforced Concrete Structures Exposed to Cracking and Chlorides. In Assessment, Upgrading and Refurbishment of Infrastructures; IABSE: Rotterdam, The Netherlands, 2013; pp. 204–205.
Bui, H.T.; Tan, K.H. Time-Dependent Nonuniform Numerical Model of Corrosion Process and Consequent Corrosion-Induced Concrete Cracking under Chloride Attack. Structures 2023, 52, 332–347.
Nguyen, P.T.; Bastidas-Arteaga, E.; Amiri, O.; El Soueidy, C.P. An Efficient Chloride Ingress Model for Long-Term Lifetime Assessment of Reinforced Concrete Structures Under Realistic Climate and Exposure Conditions. Int. J. Concr. Struct. Mater. 2017, 11, 199–213.
Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 9781119387596.
Lounis, Z.; Daigle, L.; Cusson, D.; Almansour, H. A multi-objective approach for the management of aging critical highway bridges. In Aging Infrastructures Workshop; Columbia University: New York, NY, USA, 2009; pp. 1–20.
Tolliver, D.; Lu, P. Analysis of Bridge Deterioration Rates: A Case Study of the Northern Plains Region. J. Transp. Res. Forum 2011, 50, 87–100.
Zakeri, J.-A.; Shahriari, S. Developing A Deterioration Probabilistic Model for Rail Wear. Int. J. Traffic Transp. Eng. 2012, 1, 13–18.
Ranjith, S.; Setunge, S.; Gravina, R.; Venkatesan, S. Deterioration Prediction of Timber Bridge Elements Using the Markov Chain. J. Perform. Constr. Facil. 2013, 27, 319–325.
Kotze, R.; Ngo, H.; Seskis, J. Improved Bridge Deterioration Models, Predictive Tools and Costs; Austroads Ltd.: Sydney, Australia, 2015; ISBN 978-1-925294-46-0.
Muñoz, Y.F.; Paz, A.; Fuente-Mella, H.D.; La; Fariña, J.V.; Sales, G.M. Estimating Bridge Deterioration for Small Data Sets Using Regression and Markov Models. Int. J. Urban Civ. Eng. 2016, 2016, 663–670.
Bastidas-Arteaga, E.; Schoefs, F. Stochastic Improvement of Inspection and Maintenance of Corroding Reinforced Concrete Structures Placed in Unsaturated Environments. Eng. Struct. 2012, 41, 50–62.
Zhang, Y.; Kim, C.W.; Tee, K.F.; Lam, J.S.L. Optimal Sustainable Life Cycle Maintenance Strategies for Port Infrastructures. J. Clean. Prod. 2017, 142, 1693–1709.
Kwon, S.J.; Na, U.J.; Park, S.S.; Jung, S.H. Service Life Prediction of Concrete Wharves with Early-Aged Crack: Probabilistic Approach for Chloride Diffusion. Struct. Saf. 2009, 31, 75–83.
Bastidas-Arteaga, E.; Bressolette, P.; Chateauneuf, A.; Sánchez-Silva, M. Probabilistic Lifetime Assessment of RC Structures under Coupled Corrosion-Fatigue Deterioration Processes. Struct. Saf. 2009, 31, 84–96.
Bastidas-Arteaga, E.; Chateauneuf, A.; Sánchez-Silva, M.; Bressolette, P.; Schoefs, F. Influence of Weather and Global Warming in Chloride Ingress into Concrete: A Stochastic Approach. Struct. Saf. 2010, 32, 238–249.
Molyneaux, T.C.K.; Law, D.W.; Collins, F.; Blin, F.; Zou, R.; Siamphukdee, K. Probabilistic Modelling of the Deterioration of Reinforced Concrete Port Infrastructure. Key Eng. Mater. 2013, 569–570, 207–214.
Homer, R.M.; Law, D.W.; Molyneaux, T.C.K. Probability Distribution Functions for Cover Used in 3-D Model Simulating Concrete Deterioration in Port Assets. J. Phys. Conf. Ser. 2015, 628, 012038.
Pang, L.; Li, Q. Service Life Prediction of RC Structures in Marine Environment Using Long Term Chloride Ingress Data: Comparison between Exposure Trials and Real Structure Surveys. Constr. Build. Mater. 2016, 113, 979–987.
Yu, B.; Ning, C.; Li, B. Probabilistic Durability Assessment of Concrete Structures in Marine Environments: Reliability and Sensitivity Analysis. China Ocean Eng. 2017, 31, 63–73.
Pereira, D.D.; Moreira, V.N.; Camões, A.; Matos, J.C. Assessing the Life Cycle of Existing Maritime Structures—Application to a Harbour Bridge in Porto Port. In High Tech Concrete: Where Technology and Engineering Meet; Hordijk, D.A., Lukovic, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1707–1714. ISBN 978-3-319-59471-2/978-3-319-59470-5.
Pang, S.; Yu, M.; Zhu, H.; Yi, C. The Corrosion Probability and Flexural Strength of an RC Beam under Chloride Ingress Considering the Randomness of Temperature and Humidity. Materials 2020, 13, 2260.
Mauch, M.; Madanat, S. Semiparametric Hazard Rate Models of Reinforced Concrete Bridge Deck Deterioration. J. Infrastruct. Syst. 2001, 7, 49–57.
Kaveh, A.; Eslamlou, A.D. Introduction. In Metaheuristic Optimization Algorithms in Civil Engineering: New Applications. Studies in Computational Intelligence; Springer: Cham, Switzerland, 2020; Volume 900, pp. 1–7.
Mašović, S.; Hajdin, R. Modelling of Bridge Elements Deterioration for Serbian Bridge Inventory. Struct. Infrastruct. Eng. 2014, 10, 976–987.
Morcous, G.; Rivard, H.; Hanna, A.M. Modeling Bridge Deterioration Using Case-Based Reasoning. J. Infrastruct. Syst. 2002, 8, 86–95.
Dong, Y.; Frangopol, D.M.; Sabatino, S. Optimizing Bridge Network Retrofit Planning Based on Cost-Benefit Evaluation and Multi-Attribute Utility Associated with Sustainability. Earthq. Spectra 2015, 31, 2255–2280.
Elbehairy, H.; Elbeltagi, E.; Hegazy, T.; Soudki, K. Comparison of Two Evolutionary Algorithms for Optimization of Bridge Deck Repairs. Comput. Civ. Infrastruct. Eng. 2006, 21, 561–572.
Elbehairy, H. Bridge Management System with Integrated Life Cycle Cost Optimization. Doctotal Thesis, University of Waterloo, Waterloo, ON, Canada, 2007.
Sataloff, R.T.; Johns, M.M.; Kost, K.M. Neural Networks in a Softcomputing Framework; Springer: London, UK, 2006; ISBN 1-84628-302-7.
Hasan, M.S. Deterioration Prediction of Concrete Bridge Components Using Artificial Intelligence and Stochastic Methods. Doctoral Thesis, RMIT University, Melbourne, Australia, 2015.
Kubat, M. An Introduction to Machine Learning; Springer: Berlin, Germary, 2017; ISBN 9783319639130.
Ukrainczyk, N.; Banjad, I.; Ukrainczyk, V. Application of Neural Network in Predicting Damage of Concrete Structures Caused by Chlorides. In Proceedings of the International Symposium: Durability and Maintenance of Concrete Structures, Dubrovnik, Croatia, 21–23 October 2004; pp. 187–194.
Asghshahr, M.S.; Rahai, A.; Ashrafi, H. Prediction of Chloride Content in Concrete Using ANN and CART. Mag. Concr. Res. 2016, 68, 1085–1098.
Roxas, C.L.C.; Lejano, B.A. An artificial neural network model for the corrosion current density of steel in mortar mixed with seawater. GEOMATE J. 2019, 16, 79–84.
Chou, J.-S.; Ngo, N.-T.; Chong, W.K. The Use of Artificial Intelligence Combiners for Modeling Steel Pitting Risk and Corrosion Rate. Eng. Appl. Artif. Intell. 2017, 65, 471–483.
Mohammadi, E.; Kashani, A.; Kim, T.; Arashpour, M. Concrete Chloride Diffusion Modelling Using Marine Creatures-Based Metaheuristic Artificial Intelligence. J. Clean. Prod. 2022, 374, 134021.
Rincon, L.F.; Matos, J.C.; Pereira, E.; Marcelino, J.; Santos, L.O.; Muñoz, Y.F.; Bastidas-Arteaga, E. Novel Trends on the Assessment and Management of Maritime Infrastructures: Outcomes from GIIP Project. In Proceedings of the Eighth World Conference on Structural Control and Monitoring (8WCSCM), Orlando, FL, USA, 5–8 June 2022.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Civil; Engineering, Marine

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Luis F. Rincon

Yina M. Moscoso

Ameur El Amine Hamami

José C. Matos

Emilio Bastidas-Arteaga

View Times: 79

Update Date: 01 Mar 2024

Table of Contents

Video Upload Options

Confirm