Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Teresa Donateo | -- | 7548 | 2024-02-20 10:27:04 | | | |
| 2 | Camila Xu | Meta information modification | 7548 | 2024-02-22 07:04:20 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Donateo, T. Open-Cathode PEM Fuel Cells. Encyclopedia. Available online: https://encyclopedia.pub/entry/55213 (accessed on 07 January 2026).
Donateo T. Open-Cathode PEM Fuel Cells. Encyclopedia. Available at: https://encyclopedia.pub/entry/55213. Accessed January 07, 2026.
Donateo, Teresa. "Open-Cathode PEM Fuel Cells" Encyclopedia, https://encyclopedia.pub/entry/55213 (accessed January 07, 2026).
Donateo, T. (2024, February 20). Open-Cathode PEM Fuel Cells. In Encyclopedia. https://encyclopedia.pub/entry/55213
Donateo, Teresa. "Open-Cathode PEM Fuel Cells." Encyclopedia. Web. 20 February, 2024.
Copy Citation
Fuel cells were first introduced in aircraft as auxiliary power units; however, in recent years, there has been an increasing interest in using fuel cells, batteries, and, sometimes, supercapacitors for the electric propulsion of small aerial vehicles. Open cathode fuel cells are characterized by a light and simple balance of plant but the control of temperature is quite critical under variable conditions of load and altitude, typical of the aerospace application.
hydrogen
open-cathode PEMFC
balance of plant
UAM
UAV
1. Introduction
The hydrogen economy is one of today’s most promising paths to obtaining cleaner energy and propulsion systems. Fuel cells were first introduced in aircraft as auxiliary power units; however, in recent years, there has been an increasing interest in using fuel cells, batteries, and, sometimes, supercapacitors for the electric propulsion of small aerial vehicles [1]. Compared with internal combustion engines fueled with hydrogen, fuel cells guarantee higher conversion efficiency and no direct emission. Thanks to the superior energy density of hydrogen and the high specific power of fuel cells, propulsion systems with fuel cells can guarantee lower takeoff weights and longer ranges than aerial vehicles powered by batteries alone [2]. Another advantage of fuel cells for aerospace applications is the possibility to use by-products (water, heat, and oxygen-depleted air) to save resources and reduce take-off mass [3].
Three types of fuel cells can be considered for this application: proton exchange membrane fuel cells (PEMFC), direct methanol fuel cells (DMFC), and solid oxide fuel cells (SOFC) [4]. Among them, PEMFCs are characterized by the highest power density (an important feature in aerospace applications), good start–stop capabilities and the possibility to operate at low temperatures. On the other hand, this kind of fuel cell presents a higher cost because of the use of expensive catalysts, materials, manufacturing technologies, and ancillaries. Furthermore, they show very poor tolerance to CO and thus require a very high purity of hydrogen unless high-temperature solutions are adopted. Since PEMFCs are the most used fuel cell in urban air mobility (UAM) and unmanned aerial vehicles (UAVs), this research concentrates on this kind of technology.
The cell of PEMFC consists of a membrane electrolyte assembly (MEA) included between the gas diffusion layers and the cathode and the anode flow channels. Bipolar plates, sealing gaskets, and current collectors complete the cell (see Figure 1). The cell converts the chemical energy of hydrogen into electricity with the following overall reaction:

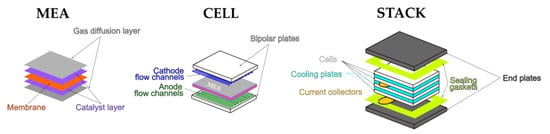
Figure 1. Structure of a PEM fuel cell.
During normal operation, the average voltage of a single cell ranges between 0.6 and 0.7 V. To achieve the required voltage, a certain number of cells are connected in series forming a stack [5]. The nominal electric power of the stack depends on the active area of the MEA and the number of cells connected in series.
To optimize the electrochemical conversion without sacrificing the thermodynamic efficiency, the temperature of the stack is usually kept between 60 °C and 80 °C. To increase the tolerance to CO and reduce the need for a catalyst, high-temperature PEMFCs can be adopted [6].
To make the conversion of hydrogen energy possible, it is necessary to provide the reactants, keep the working temperature within optimal values by an appropriate cooling system, and control the voltage with an electric power control system. The correct humidification of the membrane is also a critical aspect and may require a separate water management circuit [7]. All of these sub-systems form the so-called balance of plant (BOP) [5] and absorb parasitic electric power from the stack during normal operation and from a battery at the start-up.
For a power request below 6 kW, it is possible to adopt a simple configuration where the same flow of air is used both to deliver oxygen to the cathode and as a cooling medium. This kind of PEMFC is called open-cathode (OCPEMFC). For applications like cell phones and emergency chargers that require very low power, the PEMFC can be free-breathing; that said, generally, the air is forced through the OCPEMFC using a fan [8]. A review of heat and water management systems in an OCPEMFC is performed in [9] either at single-cell or stack level.
In the aerospace field, there is an effort to extend the range of applications of air-cooled fuel cells [10][11] by accurately selecting the location of the fuel cell in the fuselage [12][13] and by adopting advanced cooling techniques [14][15][16]. Edge cooling can increase the stack power by more than 15% [9]. In [17], heat spreaders and/or heat pipes have been proposed for a medium-scale (<10 kW) fuel cell. Such solutions increase the volume of the stack and require a higher flow of air than conventional air-cooling solutions but can be effective for UAVs [18]. A high-temperature air-cooled PEMFC is used in the Zeroavia project [11]. Another option is the modular construction of fuel cell systems [19] by connecting more lightweight air-cooled devices in series or parallel. This solution can be more suitable than larger, heavier, and more complicated single-stack water-cooled systems [20]. On the other hand, several technological issues must be considered in the association of elementary stacks: the partition of power between the several modules, the power electronic interface, and the auxiliary devices [21]. A power electronic interface is used in [21] to adapt the fuel cell voltage to that of the load by considering that each stack can have a different polarization curve.
For stacks with a nominal power greater than 10 kW, the heat released by the electrochemical reaction cannot be rejected without adopting a liquid cooling circuit and the flow of reactants needs to be increased to support the electrochemical reaction. To solve these issues, a closed-cathode configuration (CCPEMFC) where the air is compressed to the desired level is adopted [8]. Automotive fuel cell stacks in the range of 50–90 kW are liquid-cooled using deionized water or a mixture of water and glycol. Liquid-cooled PEMFCs are used in the ENFICA-FC [22] project as well as in Sigma-4 ultralight aircraft [23]. CCPEMFCs are characterized by a complex balance of plants that require a higher parasitic power, in particular for the compressor. On the other hand, their performance is less influenced by ambient conditions because it is possible to better regulate heat dissipation and membrane hydration [9]. A critical issue in this type of fuel cell is the control of the oxygen excess ratio (OER). Fuel cells operated with stoichiometric air are subject to oxygen starvation that in turn causes flooding of the stack and damage to the membrane. However, adopting high values of OER increases the parasitic power of the compressor and causes a reduction in the net power of the fuel cell. To avoid such problems and improve the performance of the stack, an OER of about 2 is generally adopted.
A review of semi-empirical models for CCPEMFCs has already been proposed by the author in a previous review paper [24]. The present investigation focuses on open-cathode fuel cell systems with forced air-cooling that will be simply referred to as OCPEMFCs.
The main control action in an OCPEMFC is the regulation of the fan flow rate to achieve the desired temperature according to the load. The hydrogen can be supplied in three possible ways: flow-through, dead-end anode, and recirculation [25]. The first one is used in laboratory tests and is based on the feeding of hydrogen in excess to remove the water diffused from the cathode to the anode. The hydrogen in excess is wasted and H2 emissions are produced. In recirculation mode, the residual hydrogen is recirculated back to the supply line by a pump or an ejector after passing through a separator to isolate the fuel from the impurities. The complexity and the high parasitic load of this solution mean that it is rarely used in aerospace applications [26][27][28]. In dead-end mode, the anode is sealed off and a solenoid valve is placed at the outlet to seal the anode. During the dead-end operation, the accumulation of impurities in the anode like inert gases and liquid water decreases the voltage of the cell. To remove such impurities and repristinate the voltage, the purge valve is opened with a frequency of activation that needs to be accurately chosen to improve fuel utilization [29]. The stack performance oscillates violently and periodically in the purging process, causing spikes in the voltage signal and hydrogen consumption [30]. A pulse width of 0.2 s is used in [31], which refers to a fixed-wing UAV. The same work also points out how the low hydrogen utilization at part load due to the purge action affects the overall efficiency of the powertrain, in particular during taxi operation while the efficiency in cruise conditions is in the range of 33–36%. In [32], the purge duration is optimized with an experimental approach applied to a single-cell PEM fuel cell. To this scope, the fuel cell power and hydrogen supplier rate were sampled with a frequency of 50 Hz.
As pointed out in [33], rapid variations in load and elevation during the flight have a great impact on the performances of aeronautics PEMFCs. A rise in flight altitude determines a reduction in air temperature, density, etc., that affects the behavior of the fan. A sudden increase in the load accelerates the electro-chemical reaction and increases hydrogen consumption without a simultaneous increase in the air flow rate due to the time lag of the BOP. This causes rapid growth of the stack temperature, which can damage the membrane [34]. To account for these effects, it is necessary to address the dynamic response of the fuel cell with appropriate models.
The effect of altitude on the behavior of the fuel cell is addressed in the scientific literature related to liquid-cooled fuel cells for road transportation. In the case of aerospace applications, only a few papers addressed this issue because of the difficulty of simulating and verifying PEMFC systems under a variable flight elevation. With a specific application to unmanned air vehicles (UAVs), the results of Atkinson et al. [35] indicated that OCPEMFC can be operated over wide ranges of temperature, relative humidity airspeed, and elevation. However, a significant reduction in the maximum power of the fuel cell is observed during the flight due to increasing ambient humidity (up to 24%), flight speed (up to 28%), and elevation (up to 20%). In aerial applications, the very dry and cold ambient air, together with the presence of dust, can harm the membrane of the fuel cell. In [18], a dome with regulated ventilation is proposed to solve this problem as well as to allow the retrieval of the water vapor generated by the fuel cell.
The scientific literature on the control of fuel cell systems is mainly focused on the regulation of heat transfer, mass flows and pressure levels, while the mismatch between the load and the fuel cell voltages is neglected. However, changes in the cathode pressure result in fluctuations in DC bus voltage [33] that in turn influence the speed regulation of the fan that supplies the air.
Fuel cell models can be classified on the basis of the level of analysis, complexity of the model, and way of encompassing dynamic effects.
Regarding the level of analysis, models for single cells and stacks concentrate on the voltage–current characteristic while system-level models of OCPEMFCs address the control of temperature with the fan and the management of the purge valve.
In relation to the underlying physics and computational effort, models are classified into black box, grey box, and white box [36]. In a black box model, input and output experimental data are correlated without any knowledge of the physical processes taking place in the system. Examples of black box models, also called data-driven models, include fuzzy logic and artificial neural networks. A black-box model is used for the control of temperature in [37]. Data-driven models have high accuracy in predicting the performance of a specific fuel cell system under a certain range of variation and require very low computational effort. This makes them suitable for online identification of operational parameters [36]. However, they have no generality. White box models, also called “mechanism models” [38][39][40], consist of algebraic and/or differential equations that implement the laws of electrochemistry, thermodynamics, and fluid mechanics. They are useful to study the effect of geometrical or operational parameters on the performance of a fuel cell. Grey box models are based on a combination of physical relationships and experimental data and offer a compromise between complexity and simplicity. Therefore, they are considered the best solution for energy management and control of fuel cells [36].
The behavior of a fuel cell system under variable load operation can be addressed either with a quasi-static or a dynamic model [41]. In the first case, the load and the boundary conditions are assumed to vary very slowly compared with the dynamic processes that take place in the system so that the fuel cell can be assumed to be always in equilibrium. Therefore, a quasi-static simulation is a sequence of static operating conditions performed over the mission duration. The goal of quasi-static models is to calculate the current and voltage of the PEMFC under very slow modifications of the load [26]. For this scope, equivalent electric circuit models with resistors and capacitor are often used. The preferred simulation environment is MATLAB Simulink [42], although other numerical tools are sometimes adopted [43]. Dynamic models are applied in the testing of the fuel cell control system and for assessing the response of the fuel cell to fast load changes [44].
In hybrid electric power systems with fuel cells, quasi-static models of the fuel cell system are generally used. However, the dynamic response of a PEMFC cannot be neglected when developing energy management strategies [36], and when the fuel cell system is subject to fast variations in load and altitude, as is the case for small drones [45][46]. A profile of the electric power request acquired on a quadcopter is reported in Figure 2.
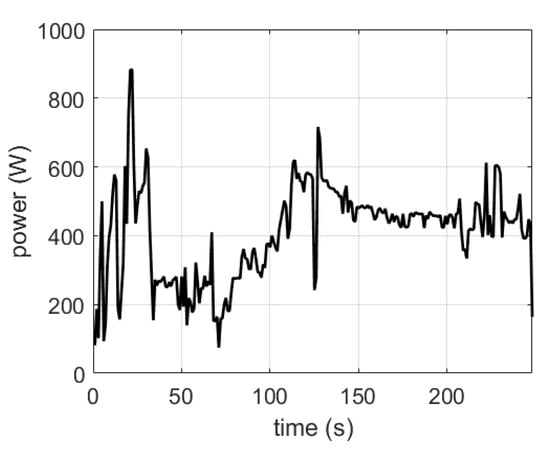
Figure 2. Recorded load power profile of a battery quadcopter [45].
The effect of the fan parasitic power on the fuel cell net efficiency and power is often neglected, and only a few experimental investigations address this aspect (Ou et al. [47], Lee et al. [48]).
In the scientific literature, there is an increasing interest in digital twins, i.e., simulation models that integrate physical models with sensor updates, historical data, and control information [49] with a bilateral mutuality between the virtual representation and the physical system [50]. In particular, the physical product modifies its real-time behavior according to the feedback generated by the digital twin. On the other hand, thanks to sensor updates and historical data, the model can precisely reflect the real-world condition of the physical body. In transportation systems, there are many uses of digital twins including increased safety, autonomous steering, smooth drive, and increased energy savings [50]. Nowadays, most of the works in the literature deal with digital twins for intelligent transport systems [51][52]. The concept of digital twins was formally defined in 2012 by NASA, which envisioned the possibilities it could entail in the aerospace industry [53]. However, the application of digital twins to fuel cell systems adopted in aerial vehicles is currently lacking, to the author’s knowledge.
2. Open-Cathode PEM Fuel Cells
A water management system is generally needed in a fuel cell to achieve a fully hydrated membrane while avoiding flooding. The control of hydration is traditionally performed with an external humidification system but can also be achieved by means of self-humidifying methods where the water generated from the reaction, Equation (1), is used to keep the desired level of hydration in the membrane. This solution is preferred in the aviation field because it reduces cost, weight, and complexity [54].
The typical configuration of a self-humidified OCPEMFC for UAV is shown in Figure 3 inclusive of the stack and the BOP. The BOP includes the hydrogen circuit, air path, electric circuit, and controller.
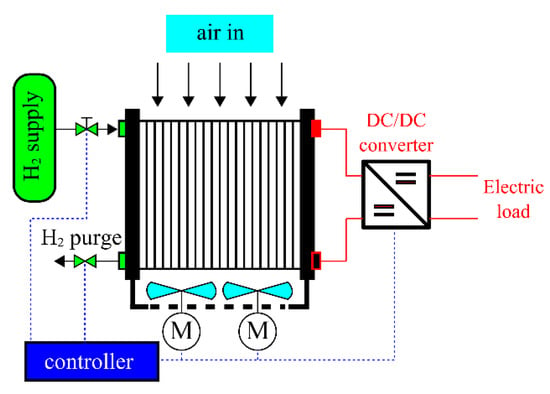
Figure 3. BOP of a self-humidified OCPEMFC. No external humidification is required because of the self-humidification process.
The hydrogen is supplied from a tank that can be of three types: pressurized vessels, cryogenic tanks, or metal-hydride storage systems [41].
The flow rate and the pressure of hydrogen are controlled using a regulation valve. The cathode is dead-end with a purge valve opened with a certain frequency to eliminate water and impurities. As explained in the introduction, the opening of the purge valve determines an outflow of hydrogen.
An inflow of air is guaranteed by the usage of one or more fans and is necessary both for providing the oxidant and as a cooling medium. The motor receives power from the stack or a battery (in particular during the start-up process). The temperature of the stack is regulated by controlling the speed of the fan motors and, therefore, the mass flow rate of the fan.
Since the voltage of the stack decreases with increasing current (i.e., load), a DC/DC converter is used to obtain the desired voltage of the electric load.
2.1. Performance and Efficiency Indexes
The gross electric power of a stack is given by:

When the OCPEMFC is analyzed at a system level, it is necessary to encompass the parasitic power of the BOP [56]. The net power of a fuel cell system is given by:

The efficiency of the stack can be expressed as:

The purging process determines a reduction in fuel utilization, particularly at low loads. To quantify this effect, the flow rate of hydrogen without purging was estimated by Verstraete et al. [62] by taking a moving average of the measured data. The fuel utilization curve of Figure 4 was obtained.
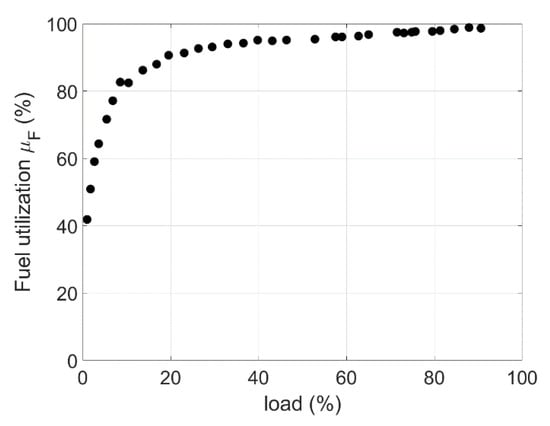
Figure 4. Fuel utilization vs. load [62].
The voltage of the fuel cell, 𝑉𝑐𝑒𝑙𝑙, is significantly inferior to 𝐸0 because of activation, ohmic, and concentration [5] losses that will be described in Section 3.
The net efficiency of a fuel cell system can be expressed as [1]:

where 𝑚˙𝐻2 is the hydrogen mass flow rate and 𝐻𝐻𝑉 is the higher heating value of hydrogen.
The net system efficiency was found to range between 32% and 49% in the power range of the H-500XP stack [57]. Typical curves of cell voltage, net efficiency, and net power vs. current are reported in Figure 5. Note that the net efficiency, unlike the gross efficiency (which follows the same trend as the cell voltage), tends to zero at low loads and is lower than the gross efficiency because it is affected by the duty cycle of the fan and by the loss of hydrogen caused by the purging action [17]. This evidences the importance of accounting for the parasitic power of the fan and the other components of the BOP.
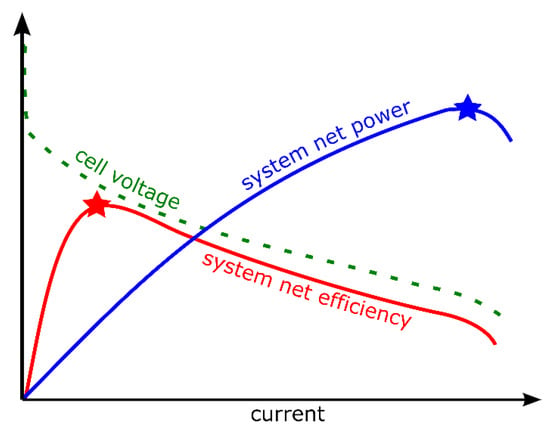
Figure 5. Typical curves of cell voltage, net efficiency, and net power vs. current.
Note that the maximum efficiency (red star in Figure 5) is obtained at low loads and high voltages while the maximum power (blue star in Figure 5) is obtained at medium-high currents and low voltages. According to the field of application, FC system designers can select the voltage that maximizes power, efficiency, or fuel utilization [68].
The performance of an OCPEMFC system can be measured also in terms of stack cooling effectiveness 𝜀 [69]:

A cooling device can be also characterized in terms of the ratio between heat removal rate and parasitic power. A well-designed cooling system can achieve an effectiveness ratio between 20% and 40%.
2.2. Fan Working Point and Speed Control
In OCPEMFCs, the role of the fan is to direct the airflow rate toward the air channels of the cathode and to overcome the major and minor head losses [70][71] of the stack.
The pressure of the air supplied to the cathode is the sum of the ambient pressure and the rise in pressure generated by the fan. The performance of a fan is expressed by its performance or characteristic curve that reports the pressure head vs. the air flow ratio. The pressure head in this application is given by:

An example of the performance curve of the fan is reported in Figure 6 together with a hypothetical stack resistance curve. The fan curve refers to the Delta FFB-0912-EHE model used in the Horizon H-1000 stack [64]. The actual air mass flow rate is obtained by intersecting the fan curve with the stack resistance curve [8], which is a quadratic function of the air flow rate. In general, the pressure head decreases when the air mass flow increases. However, most fans have a region of the performance curve where the pressure head increases with 𝑚˙𝑎𝑖𝑟 like the stack resistance curve (the instability region of Figure 6). This region is to be avoided because the fan presents unstable behavior (stall). If the fan attempts to generate more airflow, the system pressure increases, reducing the generated airflow. As airflow decreases, the system pressure also decreases, and the fan responds by generating more airflow. This induces larger changes in flow rates, which in turn can lead to cyclic behavior of the air flow rate.
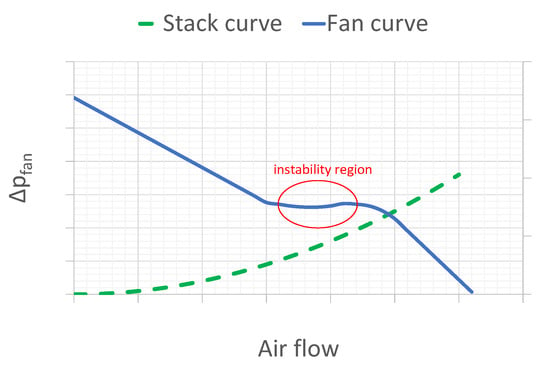
Figure 6. Typical performance of a fan and an example of stack resistance curve.
The fan must be selected so that its operating point falls in the stable part of the characteristic to guarantee a stable operation and avoid poor fan efficiency and wear on the fan components [72].
Centrifugal or axial fans can be adopted according to the desired air velocity, and two or more fans can be connected or in series to change the operating point. A comparison of centrifugal and axial fans with the different rated speeds is performed in [72]. However, the working point is affected slightly by the cell voltage and strongly by the fan speed.
A variable rotation speed allows the cooling air flow rate to be adjusted to regulate the stack temperature, reducing the noise of the fan and saving energy when full speed is not required. There are two main ways to control the speed of the fan: variable DC voltage supply and PWM (pulse-width modulation). In the first case, a series resistor is used to cause a voltage drop in the supply wire. The lower bound of voltage is limited by the need to avoid a stall in the fan. In the second and most common case, the speed of the fan is determined by the width of the PWM duty cycle while the input voltage is constant. A duty cycle of 40% keeps the electric motor on for 40% of the total time of the PWM signal, and the other 60% of the time, it will remain off. PWM is preferred because it does not generate additional heat, reduces noise thanks to the high-frequency driving signal, and increases the operational speed bandwidth [73]. With this technique, the speed variation of cooling fans is within 30–100% of the rated speed and the minimum speed achieved with PWM controllers is much lower than with DC fans. The duty cycle D is expressed as the ratio between the duration of pulse width and the period of the signal cycle. The fan speed response is almost linear with the PWM duty cycle in the operational bandwidth (D > 30%) [73].
2.3. Testing Procedure and Facilities
-
Overall performance (I–V curve, net power curve);
-
Relative effect of the three main loss mechanisms;
-
Mass transport proprieties;
-
Parasitic losses;
-
Structure of catalyst, electrodes and flows;
-
Heat balance;
-
Lifetime issues;
According to [1], the most useful methods for electrochemical characterizations of the stack are current–voltage measurements, current interrupt tests, electrochemical impedance spectroscopy, and cyclic voltammetry.
Current–voltage measurements are usually performed with galvanostatic techniques where the current is controlled by the user and the resulting voltage is recorded. In the first case, the current is gradually scanned in time from zero to the maximum value, and the voltage is measured after a long relaxation time. As pointed out in [1], it is important to ensure that steady-state conditions are reached. Moreover, test conditions must be carefully controlled and documented. To address the first point, it is necessary to conduct a series of measurements at different speeds. For the second point, a warm-up must be performed by operating the cell at a fixed current load for 30–60 min before testing and recording the fuel cell temperatures of the gases and of the stack during the measurements. The pressure at the inlets and outlets and the flows of reactants and products must be also recorded.
In the current interrupt measurement, a current is abruptly imposed or withdrawn, and the time signal of voltage is measured until it approaches the steady stage value. This method is used in [63] to tune a dynamic model of the fuel cell stack.
In electrochemical impedance spectroscopy, a sinusoidal perturbation is applied to the system and the amplitude and phase shifts of the resulting signal are measured. By repeating the test over a wide range of frequencies, an impedance spectrum is obtained. The difference between the low-frequency intercept and the high-frequency intercept of the real axis of an impedance spectrum represents the resistance of the electrode processes while the high-frequency intercept is the ohmic resistance [35].
Regarding the relative effect of losses in a stack, O’Hayre et al. [4] explain how it is possible to separate the individual contributions of activation, ohmic, and concentration losses from a current–voltage curve. As for the relative effect of the three loss mechanisms, from the results reported in [68][74], the most relevant contribution is that associated with activation losses.
The test bench of whole OCPEMFC systems usually consists of data acquisition systems, controllers for the fan voltage and the purging time, thermocouples for temperature measurement, and a flow-rate measurement for hydrogen flow rate [14][37]. A programmable electronic load is used to reproduce a variable current load. Generally, tests are performed in rooms where the temperature and humidity are not controlled, and their values are sometimes not even recorded. However, the details of pressure, temperature, humidity, and relaxation times are rarely reported in the scientific literature.
Altitude chambers have been proposed to reproduce the operation of a fuel cell system at high (<11,000 m) and very high altitudes (>11,000 m). Often, these chambers allow the control of pressure while humidity and temperature can be monitored. An environmental test chamber was included in a wind tunnel by Atkinson et al. [35] to study the effect of altitude on a single cell. The test system adopted in [35] includes a frequency response analyzer for the analysis of the impedance spectrum. Saadi et al. [26] used electrochemical impendence spectroscopy (EIS) to investigate the phenomena of diffusion and charge transfer. Wind tunnels are employed in [18] to study edge cooling in a UAV and in [75] to measure the convective heat transfer coefficient of a PEM. In [30], the stack is tested in an environmental chamber that allows the control of humidity, temperature, and oxygen concentration.
2.4. Transient Phenomena in an OCPEMFC
In applications characterized by rapid variation of loads like UAVs, the analysis of the dynamic behavior of PEMFCs is of the utmost importance [55][76]. One of the limitations of fuel cells compared with batteries and supercapacitors is the slower response to variable load profiles like that reported in Figure 2. A transient of 20–30 s from no load to rated power was measured in [60] for a fuel cell. In [61], the dynamic responses to step-down (20 A–0 A) and step-up (0 A–20 A) transient loads of a 1.2 kW Ballard fuel cell and a lithium battery were found to be 1.2 s and 0.6 s, respectively. This explains the need for the fuel cell to be coupled with a battery or a supercapacitor to improve the response to fast load changes [77]. Analyzing the transient behavior of a PEMFC is also significant in the case of start-up and shut-down operations to achieve a rapid increase in the stack temperature and to avoid the degradation of the fuel cell, respectively [78].
Different interconnected dynamics processes take place in an OCPEMFC, each requiring a suitable control action to optimize the behavior of the whole system [55][78].
The control of the temperature is the most critical issue in an OCPEMFC and is achieved by acting on the speed of the fan. On the one hand, an increase in temperature accelerates the electrochemical reaction and improves the efficiency. On the other hand, a too-high temperature can damage the membrane and increase the internal resistance [79]. Moreover, high temperatures cause dehydration in the catalyst layer and reduce the cell voltage [30]. As a consequence, both performance and efficiency are degraded. The optimal temperature of the stack according to Abul-Hawa et al. [55] should be 80 °C while a range of 65–85 °C is considered in [79]. In other investigations, the reference value for temperature is varied with the load [80]. Under cold-start operation, heaters are used for a fast warm-up of the stack [37].
To avoid an excessive difference in pressure across the membrane that can damage the membrane and increase reactant crossover, it is necessary to regulate the feeding pressure of hydrogen, especially at high-altitude, where the cathode pressure is lower [55].
The humidity of the cathode air must be high to minimize the internal resistance of the fuel cell but not too high to avoid flooding. Sudden variations in the water content cause hysteresis in the dynamic polarization curve [62]. In particular, a lower voltage at a given current is obtained in the case of load reduction. The faster the load variation, the higher the degree of hysteresis. The water content in the membrane is controlled with an external circuit humidification circuit. In self-humidifying fuel cells [81], additives are adopted into the catalyst layer or in the membrane to retain the water generated by reaction (1).
During transients, it is also important to avoid starvation of reactants to preserve the performances [79][82]. Using more fuel than needed for a specified power (i.e., adopting low values of 𝜇𝐹) is a possibility, but this determines a waste of hydrogen, which is a precious energy carrier. In [79], the optimization of stack orientation is also suggested as a way to solve the problem of oxygen starvation.
At a cell level, a further dynamic phenomenon has to be considered: the double-layer capacitor effect, which happens during the regular operation of the cell and is caused by the accumulation of charge at the anode–electrolyte and electrolyte–cathode layers. However, the double-layer capacitor effect has a much smaller time constant compared with the other dynamic phenomena, as shown in Table 1.
Table 1. Time constants of the transient phenomena in open-cathode fuel cells.
The orders of magnitude of the time constants for membrane hydration and electrochemical double-layer were estimated numerically in [83] and confirmed experimentally in [62].
2.5. Control Methods
A detailed review of control methods applied to OCPEMFCs is beyond the goal of this investigation. Nevertheless, it is significant to describe the control approaches for two reasons. On the one hand, the dynamic behavior of the fuel cell is strictly related to the control actions performed on the system. On the other hand, the number of recent papers on advanced control techniques underlines the importance of making available accurate and comprehensive control-oriented models.
In an open-cathode configuration, the main control action is related to temperature and is achieved by regulating a single component, i.e., the fan [47]. This makes the air stoichiometry rate calculation more critical than in a closed-cathode fuel cell [84]. On the other hand, Ou et al. [47] pointed out that if the focus of the control is only on the temperature, oxygen starvation can happen, in particular when a low air flow is required for cooling, for example, when the fuel cell has not yet reached the optimal temperature after the start from ambient conditions. To solve this problem, Ou et al. proposed a double calculation of the excess air to avoid overheating and protect the cell from air starvation.
In [30], two dynamic states are considered: the stack temperature and the liquid water saturation. The load current and the cathode inlet air temperature are the measurable external perturbations. The control variable is the inlet air velocity through the PWM control of the fan. The output of the system is the voltage. In this investigation, a local PI controller is used to regulate the voltage of the cooling fan, and an extremum-seeking algorithm is applied to obtain the optimal temperature set point for the PI controller. However, the experimental validation revealed that this controller was not able to stabilize the voltage because of the slow system dynamics of the drying of the catalyst layer. For this reason, other controllers were proposed in a subsequent study by Strahl et al. [85]. A review of the control method for temperature can be found in [14], where three control parameters are considered: the duty cycle of the fan, the cycle time, and the difference between the average output power of the current cycle and the previous cycle.
In [47], the control objective is to maximize the net power output and prevent overheating. For this scope, the relationship between net power and the duty cycle is mapped for different load currents, and the optimal value of the fan duty ratio is obtained. Then, the same process is used to identify the minimum duty ratio that allows the fuel cell to operate in safe temperature conditions. They found that the oxygen excess ratio of power optimization requires more air flow mass than the cooling system at high loads, and at lower currents, temperature protection is more critical. The oxygen excess ratio was selected as the maximum between the value that minimizes the net power and the minimum value required to avoid overheating. The values of the optimal oxygen excess ratios were fitted using a third-degree polynomial function and used as a reference for the fan control performed with a conventional PI controller.
The classical PI or PID controller with feedback is often used for the control of OCPEMFC, but sliding mode control has recently been proposed ([82][86]) to ensure the desired value of the oxygen excess ratio. A PID controller is a simple, economical, and easy-to-implement solution for single-input–single-output systems and is therefore applied in a variety of applications including the control of a fuel cell system [87]. The method is based on the difference (error) between a measured process variable and its setpoint and applies a correction based on the proportional, integral, and derivative terms. This control method requires tuning to find the best values of the constants used in the three terms. The tuning of the PID is addressed in detail in [65], where the author identified the best setting in terms of a trade-off between fast response and reactants consumption. In the work of Strahl et al. [30] on an H-100 stack, the proportional gain of the PID is 0.8, and the integrator time constant is 20.
A review of control methods used in fuel cell systems to avoid starvation can be found in [79]. They underlined the drawbacks of classical proportional integral and derivative controllers, i.e., the inaccuracy and slow response time that can be solved by more advanced controllers like the sliding mode, adaptive, neural network, fuzzy logic [88], and model-predictive controllers. In the last case, the availability of a fast but accurate dynamic model of the fuel cell system is critical. In [89], a model predictive control (MPC) and a PID controller were designed to control the voltage at the desired value by regulating both hydrogen and air flow rates. The two controllers were compared under different operating conditions and the MPC was found to be superior in fulfilling the stabilization of the voltage. Similarly, a comparison between MPC and traditional PID is reported in [90]. Li et al. [91] developed an active disturbance rejection controller (ADRC) with a switching law for temperature regulation.
In [74], fuzzy logic is used for the control of the temperature using the temperature error, its derivative, and current as inputs and the duty cycle of the fan as an output. A constant temperature of 35 °C was set as a reference. In [88], both temperature and humidity are controlled by employing a fuzzy-based logic that controls the PWM signal of the fan and the behavior of the external humidifier. The goal of the investigation presented in [92] was the simultaneous control of current and temperature to supply the requested power with the highest possible efficiency, i.e., with the lowest consumption of hydrogen. A fuzzy logic controller (FLC) is used to reach the reference temperature (that depends on the current) while a PI controller is used to control the current. As discussed in [92], PID controllers cause large temperature overshoots because they work well for a limited operating range. Moreover, their tuning is dependent on the accuracy of the model. On the other hand, FLCs are more flexible in terms of range of operation and also work well with not very accurate models.
In most of the papers cited above, the reference temperature is assumed to be constant (see, for example, [88]) while in [80], the optimal reference temperature is expressed as a function of the current. The results reported in [30] show that, for each current, there is an optimal stack temperature and, therefore, a different PWM value. Moreover, the optimal values of the temperature in that investigation were found to be higher than the default values considered in the standard controller. This also allows a reduction in the parasitic power of the fan thanks to the lower PWM. In [14], a temperature reference-seeking algorithm is employed to determine the optimal operating temperature in variable environmental conditions. The author of this review believes this approach to be particularly suitable for aerospace applications, but a further step is required. One of the scenarios investigated in [14] is a typical mission of a UAV. However, the effect of different values of ambient pressure and temperature due to flight altitude is not considered. Their strategy allowed an increase of up to 2.78% of the net power compared with the constant duty cycle control.
To optimize the behavior of the fuel cell system, it is also possible to control the operating point of the fuel cell to ensure maximum power or maximum efficiency through the power management unit that has the role of matching the operating point of the fuel cell with the load demand, i.e., to ensure that the power generated by the stack is equal to the power requested by the load [55]. Power management is needed because the voltage produced by the stack decreases when the current increases. The unstable direct current generated from the stack has to be strictly controlled to ensure the rapid delivery of the load required during fast transients [79]. A DC/DC power converter needs to be introduced between the fuel cell and the load to convert and stabilize the bus voltage [1]. An excessive change in DC/DC input current generates an insufficient supply of air. Therefore, the topology and control of the DC/DC converters must be designed and optimized in combination with the PEMFC system to improve output performances. To solve this problem, Zhao et al. [33] propose a PEMFC dynamic model that considers the disturbances of the internal load, the centrifugal compressor with its driving motors, and the external UAV power load under variable elevations and operating conditions.
Another possibility to control voltage is through hybridization. As already stated, the response of a fuel cell system to changes in demand is not comparable to that of its competitor (i.e., internal combustion engines and batteries) because its response to transient changes in load depends on the management of heat and water content, regulation of pressure and flow rate of the reactants [55]. For this reason, a secondary energy storage device (battery or capacitor) is needed to support the fuel cell during transients. Verstraete et al. [62] found that the controller developed by Horizon Energy Systems for their self-humidified stacks short circuits the stack output power every 10 s to increase the efficiency. A supercapacitor and/or a battery is needed to ensure continuous power during the short-circuiting process. In [77], a controller is developed for a fuel cell/supercapacitor system to keep the fuel cell power between the desired bounds and to limit the variation slope of the fuel cell to avoid starvation. Hybrid systems with batteries or supercapacitors can be passive or active [46]. In a passive system, no DC/DC converter is used; therefore, the voltage of the two systems (the fuel cell and the secondary storage system) must be similar. This reduces the weight and complexity but does not allow operation flexibility. A review of hybrid electric configurations with fuel cells for UAV applications can be found in [93].
2.6. Effect of Altitude and Cold Start
The variation in ambient temperature, pressure, and relative humidity with elevation can degrade the fuel cell performances and make the thermal management of the fuel cell system [94] more difficult. In fact, the request of air velocity and volumetric flow rate for the cooling of the fuel cell [75] increases with altitude because of the lower density. Since the increase in air velocity is smaller than the density variation, the Reynolds number of the flow also decreases.
The impact of vibration, cathode air starvation, low pressure, and cold start on PEMSs utilized in high-altitude environments is addressed in [95]. As the altitude rises, the drop in temperature and pressure and cathode air starvation cause a decline in the cell performance due to damage to the membrane electrode assembly. The effect of low pressure can be overcome by increasing the cathode air flow rate, but it is necessary to monitor the membrane humidity. A critical value of the air stoichiometric ratio must not be reached to prevent the membrane from drying.
Altitude affects the behavior of both closed-cathode and open-cathode fuel cells [67]. The effect of altitude on voltage and power in OCPEMFCs was experimentally evaluated for a single-cell system [35]. The fuel cell was tested in a depressurized chamber to simulate the pressure up to 3239 m and a decrease of 17% was found in the cell power. This reduction is suggested to be due to higher activation losses due to the operation at lower oxygen partial pressure. Moreover, the ohmic resistance increases because of the low cell temperature and relative humidity. On the other hand, the cell can dissipate waste heat more effectively at high altitudes thanks to the lower ambient temperature. Therefore, the maximum current density of the cell increases. However, as pointed out in [35], it is not possible to associate such variation only to altitude because the fuel cell is highly sensitive to ambient relative humidity and temperature.
The authors of [35] also pointed out how the availability of cool air at high temperatures could enable the removal of many traditional BOP components. The implementation of the open-cathode flexible fuel cell to cover the airframe is suggested for UAVs while hollow structures like the wings of fuselage can be used for hydrogen storage. On the other hand, this solution does not allow control of the fuel cell stack and, therefore, can cause the degradation of the cell performance when the temperature. They found that the forced airflow has little influence on OCPEMFC performance at low and intermediate cell voltage (<0.65 V).
When the stack works at an ambient temperature under 0 °C, the water produced by the reaction can solidify and the increase in water volume can destroy the MEA. To avoid such a problem, it is necessary to ensure that the heating rate is more rapid than the freezing rate of water by employing shutdown purging, external heating, etc. [69][95].
References
- Xu, L.; Huangfu, Y.; Ma, R.; Xie, R.; Song, Z.; Zhao, D.; Yang, Y.; Wang, Y.; Xu, L. A Comprehensive Review on Fuel Cell UAV Key Technologies: Propulsion System, Management Strategy, and Design Procedure. IEEE Trans. Transp. Electrif. 2022, 8, 4118–4139.
- Xiao, C.; Wang, B.; Zhao, D.; Wang, C. Comprehensive investigation on Lithium batteries for electric and hybrid-electric unmanned aerial vehicle applications. Therm. Sci. Eng. Prog. 2023, 38, 101677.
- Zakhvatkin, L.; Schechter, A.; Avrahami, I. Water Recuperation from Hydrogen Fuel Cell during Aerial Mission. Energies 2022, 15, 6848.
- O’Hayre, R.; Colella, W.; Cha, S.-W.; Prinz, F.B. Fuel Cell Fundamentals; Wiley: Hoboken, NJ, USA, 2016.
- Larmine, J.; Dicks, A. Fuel Cell Systems Explained; Wiley: Hoboken, NJ, USA, 2003; ISBN 9780470848579.
- Barreras, F.; Lozano, A.; Barroso, J.; Roda, V.; Maza, M. Theoretical Model for the Optimal Design of an Air cooling System of Polymer Electrolyte Fuel cell. Application for a High-temperature PEMFC. Fuel Cells 2013, 13, 227–237.
- Squadrito, G.; Maggio, G.; Passalacqua, E.; Lufrano, F.; Patti, A. An empirical equation for polymer electrolyte fuel cell (PEFC) behaviour. J. Appl. Electrochem. 1999, 29, 1449–1455.
- Ishaku, J.; Lotfi, N.; Zomorodi, H.; Landers, R.G. Control-oriented modeling for open-cathode fuel cell systems. In Proceedings of the 2014 American Control Conference—ACC 2014, Portland, OR, USA, 4–6 June 2014; pp. 268–273.
- Nóbrega, P.H.A. A review of physics-based low-temperature proton-exchange membrane fuel cell models for system-level water and thermal management studies. J. Power Sources 2023, 558, 232585.
- Wright, S.; Aaltonen, J. Fuel cells and novel thermal management advancements required for aviation. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences ICAS2022, Stockholm, Sweden, 4–9 September 2022; The International Council of the Aeronautical Sciences: Bonn, Germany, 2022.
- Nexa™ (310-0027) Power Module User’s Manual MAN5100078. Available online: http://faculty.stust.edu.tw/~wcchang/MAN5100078.pdf (accessed on 5 September 2023).
- Kim, T.; Kwon, S. Design and development of a fuel cell-powered small unmanned aircraft. Int. J. Hydrogen Energy 2012, 37, 615–622.
- Pratt, J.W.; Brouwer, J.; Samuelsen, G.S. Performance of proton exchange membrane fuel cell at high-altitude conditions. J. Propuls. Power 2007, 23, 437–444.
- Wang, Y.-X.; Chen, Q.; Zhang, J.; He, H. Real-time power optimization for an air-coolant proton exchange membrane fuel cell based on active temperature control. Energy 2021, 220, 119497.
- Chen, F.; Yu, Y.; Gao, Y. Temperature Control for Proton Exchange Membrane Fuel Cell based on Current Constraint with Consideration of Limited Cooling Capacity. Fuel Cells 2017, 17, 662–670.
- Tolj, I.; Penga, Ž.; Vukičević, D.; Barbir, F. Thermal management of edge-cooled 1 kW portable proton exchange membrane fuel cell stack. Appl. Energy 2020, 257, 114038.
- Xing, S.; Zhao, C.; Zou, J.; Zaman, S.; Yu, Y.; Gong, H.; Wang, Y.; Chen, M.; Wang, M.; Lin, M.; et al. Recent advances in heat and water management of forced-convection open-cathode proton exchange membrane fuel cells. Renew. Sustain. Energy Rev. 2022, 165, 112558.
- Zakhvatkin, L.; Schechter, A.; Buri, E.; Avrahami, I. Edge Cooling of a Fuel Cell during Aerial Missions by Ambient Air. Micromachines 2021, 12, 1432.
- Rathke, P.; Thalau, O.; Kallo, J.; Schirmer, J.; Stephan, T. Long Distance Flight Testing with the Fuel Cell Powered Aircraft Antares DLR-H2. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Stuttgart, Germany, 10–12 September 2013; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV.: Bonn, Germany, 2013. Document ID: 301219.
- Dudek, M.; Raźniak, A.; Rosół, M.; Siwek, T.; Dudek, P. Design, Development, and Performance of a 10 kW Polymer Exchange Membrane Fuel Cell Stack as Part of a Hybrid Power Source Designed to Supply a Motor Glider. Energies 2020, 13, 4393.
- De Bernardinis, A.; Péra, M.C.; Garnier, J.; Hissel, D.; Coquery, G.; Kauffmann, J.M. Fuel cells multi-stack power architectures and experimental validation of 1 kW parallel twin stack PEFC generator based on high frequency magnetic coupling dedicated to on board power unit. Energy Convers. Manag. 2008, 49, 2367–2383.
- Romeo, G.; Cestino, E.; Correa, G.; Borello, F. A fuel cell-based propulsion system for general aviation aircraft: The ENFI-CA-FC experience. SAE Int. J. Aerosp. 2011, 4, 724–737.
- Geliev, A.; Varyukhin, A.; Zakharchenko, V.; Kiselev, I.; Zhuravlev, D. Conceptual Design of an Electric Propulsion System Based on Fuel Cells for an Ultralight Manned Aircraft. In Proceedings of the 2019 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 21–25 October 2019; pp. 1–17.
- Donateo, T. Semi-Empirical Models for Stack and Balance of Plant in Closed-Cathode Fuel Cell Systems for Aviation. Energies 2023, 16, 7676.
- Zhu, K.-Q.; Ding, Q.; Xu, J.-H.; Yang, C.; Zhang, J.; Zhang, Y.; Huang, T.-M.; Wan, Z.-M.; Wang, X.-D. Dynamic performance for a kW-grade air-cooled proton exchange membrane fuel cell stack. Int. J. Hydrogen Energy 2022, 47, 35398–35411.
- Saadi, A.; Becherif, M.; Hissel, D.; Ramadan, H. Dynamic modeling and experimental analysis of PEMFCs: A comparative study. Int. J. Hydrogen Energy 2017, 42, 1544–1557.
- Zeng, T.; Zhang, C.; Huang, Z.; Li, M.; Chan, S.H.; Li, Q.; Wu, X. Experimental investigation on the mechanism of variable fan speed control in Open cathode PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 24017–24027.
- Wu, D.; Peng, C.; Yin, C.; Tang, H. Review of System Integration and Control of Proton Exchange Membrane Fuel Cells. Electrochem. Energy Rev. 2020, 3, 466–505.
- Yang, C.-W.; Chen, Y.-S. A mathematical model to study the performance of a proton exchange membrane fuel cell in a dead-ended anode mode. Appl. Energy 2014, 130, 113–121.
- Strahl, S.; Husar, A.; Puleston, P.; Riera, J. Performance Improvement by Temperature Control of an Open-Cathode PEM Fuel Cell System. Fuel Cells 2014, 14, 466–478.
- Bradley, T.H.; Moffitt, B.A.; Mavris, D.N.; Parekh, D.E. Development and experimental characterization of a fuel cell powered aircraft. J. Power Sources 2007, 171, 793–801.
- Lin, Y.-F.; Chen, Y.-S. Experimental study on the optimal purge duration of a proton exchange membrane fuel cell with a dead-ended anode. J. Power Sources 2017, 340, 176–182.
- Zhao, D.; Xia, L.; Dang, H.; Wu, Z.; Li, H. Design and control of air supply system for PEMFC UAV based on dynamic decoupling strategy. Energy Convers. Manag. 2022, 253, 115159.
- Peng, H.; Stefanopoulou, A.G. Simulation and analysis of transient fuel cell system performance-based on a dynamic reactant flow model. In Proceedings of the IMECE’02, ASME International Mechanical Engineering Congress & Exposition, New Orleans, LA, USA, 17–22 November 2002.
- Atkinson, R.W.; Hazard, M.W.; Rodgers, J.A.; Stroman, R.O.; Gould, B.D. An Open-Cathode Fuel Cell for Atmospheric Flight. J. Electrochem. Soc. 2017, 164, F46–F54.
- Kandidayeni, M.; Macias, A.; Amamou, A.; Boulon, L.; Kelouwani, S.; Chaoui, H. Overview and benchmark analysis of fuel cell parameters estimation for energy management purposes. J. Power Sources 2018, 380, 92–104.
- Sun, L.; Jin, Y.; You, F. Active disturbance rejection temperature control of open-cathode proton exchange membrane fuel cell. Appl. Energy 2020, 261, 114381.
- Hu, M.; Zhao, R.; Pan, R.; Cao, G. Disclosure of the internal mechanism during activating a proton exchange membrane fuel cell based on the three-step activation method. Int. J. Hydrogen Energy 2021, 46, 3008–3021.
- Zhan, Y.; Guo, Y.; Zhu, J.; Liang, B.; Yang, B. Comprehensive influences measurement and analysis of power converter low frequency current ripple on PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 31352–31359.
- Tan, B.; Chen, H.; Quan, R.; Quan, S.; Zhou, Y. Study on data-driven PEMFC humidity mechanism soft-sensing model. J. Phys. Conf. Ser. 2019, 1423, 012043.
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, Introduction to Modeling and Optimization, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013.
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. J. Prog. Energy Combust. Sci. 2020, 80, 100859.
- Wang, C.; Nehrir, M.; Shaw, S. Dynamic Models and Model Validation for PEM Fuel Cells Using Electrical Circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451.
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a Proton-Exchange Membrane Fuel Cell’s Model Parameters by Means of an Evolution Strategy. IEEE Trans. Ind. Inform. 2015, 11, 548–559.
- Boukoberine, M.N.; Zia, M.F.; Benbouzid, M.; Zhou, Z.; Donateo, T. Hybrid fuel cell powered drones energy management strategy improvement and hydrogen saving using real flight test data. Energy Convers. Manag. 2021, 236, 113987.
- Boukoberine, M.N.; Donateo, T.; Benbouzid, M. Optimized energy management strategy for hybrid fuel cell powered drones in persistent missions using real flight test data. IEEE Trans. Energy Convers. 2022, 37, 2080–2091.
- Ou, K.; Wang, Y.; Kim, Y. Performance Optimization for Open-cathode Fuel Cell Systems with Overheating Protection and Air Starvation Prevention. Fuel Cells 2017, 17, 299–307.
- Lee, C.-H.; Yang, J.-T. Modeling the Ballard-Mark-5 proton exchange membrane fuel cell with power converters for applications in autonomous underwater vehicles. J. Power Sources 2011, 196, 3810–3823.
- Vandana, G.A.; Panigrahi, B.K. Multi-dimensional digital twin of energy storage system for electrical vehicles: A brief review. Energy Storage Early View 2021, 3, e242.
- Bhatti, G.; Mohan, H.; Singh, R. R Towards the future of smart electric vehicles: Digital twin technology. Renew. Sustain. Energy Rev. 2021, 141, 110801.
- Li, Y.; Wang, S.; Duan, X.; Liu, S.; Liu, J.; Hu, S. Multi-objective energy management for Atkinson cycle engine and series hybrid electric vehicle based on evolutionary NSGA-II algorithm using digital twins. Energy Convers. Manag. 2021, 230, 113788.
- Kamran, S.S.; Haleem, A.; Bahl, S.; Javaid, M.; Nandan, D.; Verma, A.S. Role of smart materials and digital twin (DT) for the adoption of electric vehicles in India. Mater. Today Proc. 2022, 52, 2295–2304.
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and U.S. Air DT9 Force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012.
- Subin, K.; Jithesh, P.K. Experimental study on self-humidified operation in PEM fuel cells. Sustain. Energy Technol. Assess. 2018, 27, 17–22.
- Abul-Hawa, A.A.; Ebaid, M.S.; Bhinder, F.S.; Calay, R.K. Control strategy for polymer electrolyte membrane fuel cell system. In Proceedings of the 2006 UKACC International Conference on Control, Glasgow, UK, 30 August–1 September 2006; p. 94.
- Le, P.-L.; Singh, B.; Chen, Y.-S.; Arpornwichanop, A. An experimental study for optimizing the energy efficiency of a proton exchange membrane fuel cell with an open-cathode. Int. J. Hydrogen Energy 2021, 46, 26507–26517.
- Omran, A.; Lucchesi, A.; Smith, D.; Alaswad, A.; Amiri, A.; Wilberforce, T.; Sodré, J.R.; Olabi, A. Mathematical model of a proton-exchange membrane (PEM) fuel cell. Int. J. Thermofluids 2021, 11, 100110.
- Choe, S.-Y.; Ahn, J.-W.; Lee, J.-G.; Baek, S.-H. Dynamic Simulator for a PEM Fuel Cell System with a PWM DC/DC Converter. IEEE Trans. Energy Convers. 2008, 23, 669–680.
- Djerioui, A.; Houari, A.; Zeghlache, S.; Saim, A.; Benkhoris, M.F.; Meshabi, T.; Machmoum, M. Energy management strategy of Supercapacitor/Fuel Cell energy storage devices for vehicle applications. Int. J. Hydrogen Energy 2019, 44, 23416–23428.
- Hoogendoorn, J. Fuel Cells and Battery Hybrid System Optimization. Master’s Thesis in Aerospace Engineering, DELFT University of Technology, Delft, The Netherlands, 2018.
- Chang, V.; Gallman, J. Altitude Testing of Fuel Cell Systems for Aircraft Applications. Power Systems Conference. J. Aerosp. 2004, 113, 1943–1957.
- Verstraete, D.; Lehmkuehler, K.; Gong, A.; Harvey, J.R.; Brian, G.; Palmer, J.L. Characterisation of a hybrid, fuel-cell-based propulsion system for small unmanned aircraft. J. Power Sources 2014, 250, 204–211.
- Donateo, T.; Pacella, D.; Indiveri, G.; Ingrosso, F.; Damiani, A. Dynamic Modeling of a PEM Fuel Cell for a Low Consumption Prototype. SAE Tech. Pap. 2013, 2, 1–10.
- Saleh, I.M.M.; Ali, R.; Zhang, H. Simplified mathematical model of proton exchange membrane fuel cell based on horizon fuel cell stack. J. Mod. Power Syst. Clean Energy 2016, 4, 668–679.
- Sahel, I.M.M. Modeling, Simulation and Performance Evaluation: PEM Fuel Cells for High Altitude UAS. Ph.D. Thesis, Sheffield Hallam University, Sheffield, UK, 2015.
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. Analysis of the operating conditions influence on PEM fuel cell performances by means of a novel semi-empirical model. Int. J. Hydrogen Energy 2011, 36, 10434–10442.
- Fathy, A.; Abd Elaziz, M.; Alharbi, A.F. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845.
- Qingshan, X.; Nianchun, W.; Ichiyanagi, K.; Yukita, K. PEM Fuel Cell modeling and parameter influences of performance evaluation. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2827–2832.
- Mohamed, W.W.; Kamil, M.H.M. Hydrogen preheating through waste heat recovery of an open-cathode PEM fuel cell leading to power output improvement. Energy Convers. Manag. 2016, 124, 543–555.
- Musio, F.; Tacchi, F.; Omati, L.; Stampino, P.G.; Dotelli, G.; Limonta, S.; Brivio, D.; Grassini, P. PEMFC system simulation in MATLAB-Simulink® environment. Int. J. Hydrogen Energy 2011, 36, 8045–8052.
- Barreras, F.; Lopez, A.M.; Lozano, A.; Barranco, J.E. Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 7612–7620.
- Sasmito, A.P.; Birgersson, E.; Lum, K.W.; Mujumdar, A.S. Fan selection and stack design for open-cathode polymer electrolyte fuel cell stacks. Renew. Energy 2012, 37, 325–332.
- Arredondo, A.; Roy, P.; Wofford, E. Implementing PWM fan speed control within a computer chassis power supply. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, APEC 2005, Austin, TX, USA, 6–10 March 2005.
- Wang, Y.-X.; Qin, F.-F.; Ou, K.; Kim, Y.-B. Temperature Control for a Polymer Electrolyte Membrane Fuel Cell by Using Fuzzy Rule. IEEE Trans. Energy Convers. 2016, 31, 667–675.
- Barroso, J.; Renau, J.; Lozano, A.; Miralles, J.; Martín, J.; Sánchez, F.; Barreras, F. Experimental determination of the heat transfer coefficient for the optimal design of the cooling system of a PEM fuel cell placed inside the fuselage of an UAV. Appl. Therm. Eng. 2015, 89, 1–10.
- Wang, Y.; Wang, C.-Y. Dynamics of polymer electrolyte fuel cells undergoing load changes. Electrochim. Acta 2006, 51, 3924–3933.
- Tahri, A.; El Fadil, H.; Belhaj, F.; Gaouzi, K.; Rachid, A.; Giri, F.; Chaoui, F. Management of fuel cell power and supercapacitor state-of-charge for electric vehicles. Electr. Power Syst. Res. 2019, 160, 89–98.
- Ríos, G.M.; Becker, F.; Vorndran, A.; Gentner, C.; Ansar, S.A. Investigation of gas purging and cold storage impact on PEM fuel cell system performance for aeronautical applications. E3S Web Conf. 2022, 334, 06004.
- Daud, W.; Rosli, R.; Majlan, E.; Hamid, S.; Mohamed, R.; Husaini, T. PEM fuel cell system control: A review. Renew. Energy 2017, 113, 620–638.
- Mahjoubi, C.; Olivier, J.-C.; Skander-Mustapha, S.; Machmoum, M.; Slama-Belkhodja, I. An improved thermal control of open cathode proton exchange membrane fuel cell. 9th International Renewable Energy Congress (IREC). Int. J. Hydrogen Energy 2019, 44, 11332–11345.
- Mirfarsi, S.H.; Parnian, M.J.; Rowshanzamir, S. Self-humidifying proton exchange membranes for fuel cell applications: Advances and challenges. Processes 2020, 8, 1069.
- Kumar, S.S.; Cirrincione, M.; Lechappe, V.; Ram, K.R.; Mohammadi, A. A Simplified Control Oriented Model of an Open Cathode PEM Fuel Cell. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2415–2420.
- Wang, Y.; Wang, C.Y. Transient analysis of polymer electrolyte fuel cells. Electrochim. Acta 2005, 50, 1307–1315.
- López-Sabirón, A.M.; Barroso, J.; Roda, V.; Barranco, J.; Lozano, A.; Barreras, F. Design and development of the cooling system of a 2 kW nominal power open-cathode polymer electrolyte fuel cell stack. Int. J. Hydrogen Energy 2012, 37, 7289–7298.
- Strahl, S.; Costa-Castello, R. Temperature control of open-cathode PEM fuel cells. IFAC PapersOnLine 2017, 50, 11088–11093.
- Zhu, J.; Zou, J.; Li, X.; Peng, C. An adaptive sliding mode observer based near-optimum OER tracking control approach for PEMFC under dynamic operation condition. Int. J. Hydrogen Energy 2022, 47, 1157–1171.
- Qi, Y.; Espinoza-Andaluz, M.; Thern, M.; Li, T.; Andersson, M. Dynamic modeling and controlling strategy of polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2020, 45, 29718–29729.
- Ou, K.; Yuan, W.-W.; Choi, M.; Yang, S.; Kim, Y.-B. Performance increase for an open-cathode PEM fuel cell with humidity and temperature control. Int. J. Hydrogen Energy 2017, 42, 29852–29862.
- Zhu, J.; Zhang, P.; Li, X.; Jiang, B. Robust oxygen excess ratio control of PEMFC systems using adaptive dynamic programming. Energy Rep. 2022, 8, 2036–2044.
- Zhang, B.; Lin, F.; Zhang, C.; Liao, R.; Wang, Y.-X. Design and implementation of model predictive control for an open-cathode fuel cell thermal management system. Renew. Energy 2020, 154, 1014–1024.
- Li, X.; Qi, Y.; Li, S.; Tunestal, P.; Andersson, M. A multi-input and single-output voltage control for a polymer electrolyte fuel cell system using model predictive control method. Int. J. Energy Res. 2021, 45, 12854–12863.
- Kandidayeni, M.; Macias, F.A.; Boulon, L.; Kelouwani, S. Efficiency Enhancement of an Open Cathode Fuel Cell Through a Systemic Management. IEEE Trans. Veh. Technol. 2019, 68, 11462–11472.
- Çınar, H.; Kandemir, I.; Donateo, T. Current Technologies and Future Trends of Hydrogen Propulsion Systems in Hybrid Small Unmanned Aerial Vehicles. In Hydrogen Electrical Vehicles; Scrivener Publishing LLC: Beverly, MA, USA, 2023; pp. 75–109.
- Gong, C.; Xing, L.; Liang, C.; Tu, Z. Modeling and dynamic characteristic simulation of air-cooled proton exchange membrane fuel cell stack for unmanned aerial vehicle. Renew. Energy 2022, 188, 1094–1104.
- Song, W.J.; Chen, H.; Guo, H.; Ye, F.; Li, J.R. Research progress of proton exchange membrane fuel cells utilizing in high altitude environments. Int. J. Hydrogen Energy 2022, 47, 24945–24962.
More
Information
Subjects:
Energy & Fuels
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
2.4K
Revisions:
2 times
(View History)
Update Date:
22 Feb 2024
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




