Microstructured Optical Fibers in Ultrafast Optics

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Jinghua Sun	--	3475	2024-02-19 13:37:26	\|
2	update references and layout	Rita Xu	Meta information modification	3475	2024-02-20 02:39:11	\|

This entry is adapted from the peer-reviewed paper 10.3390/photonics11020151

With the development of laser technology, microstructured optical fibers (MOFs) have become an important part of ultrafast optics, providing excellent platforms for ultrafast laser pulse generation, amplification, and compression, promoting the development of fiber laser systems to generate high power, high pulse energy, and few-cycle duration pulses.

ultrafast optics photonic crystal fiber microstructured optical fiber

1. Introduction

Ultrafast lasers have played key roles in cutting-edge science and technology, bringing revolutionary progress in physical ^[1]^[2], biological ^[3]^[4], and chemical ^[5]^[6] sciences, as well as supplying advanced tools for modern industry. The Nobel Prize of 2023 was awarded to the field of ultrafast lasers for attosecond science. Looking back at the development of ultrafast lasers, the earliest pulsed lasers were on the millisecond scale, and in 1962, McClung et al. utilized Q-switching techniques and reduced the pulse width to the nanosecond scale ^[7]. With the advent of mode-locking techniques, the duration of the pulses could be reduced to the femtosecond scale, and in 1981, Fork et al. achieved sub-hundred femtosecond pulse output by colliding pulse mode-locking ^[8]. In 2001, Hentschel et al. used a femtosecond laser interacting with an inert gas to generate high harmonics and obtained a pulse output with a width of 650, which declared that ultrafast science had entered the attosecond stage ^[9]. This is considered one of the milestones in the history of laser science. In the history of ultrafast lasers, power, spectral width, pulse duration, and other parameters have been continuously measured. It has been able to produce a variety of ultrafast lasers, and microstructured optical fibers (MOFs) are definitely one of the important promoters due to their flexibility in the design of structure, making it possible to customize the dispersion and nonlinearity, while the two factors play a decisive role in ultrafast lasers. Ultrafast lasers generated with MOFs play an influential role in biomedicine ^[10]^[11], optical communication ^[12], precision measurement ^[13], etc., which has a great impact on either the development of science or people’s lives. MOFs also play important roles in many other fields, such as in sensing devices ^[14]^[15]^[16]^[17], etc.

2. Applications of MOFs in Ultrafast Optics

2.1. Pulse Amplification

One of the critical problems of laser amplification is heat dissipation. Fibers have a large ratio of surface-to-active volume, which makes them good mediums for laser amplification. There are many types of fiber laser amplifications: direct amplification of doped fibers, fiber Raman amplification, fiber optical parametric amplification, etc. Ultrafast laser amplifiers based on ytterbium-doped fiber can generate very high average power with pulse durations as short as tens of femtoseconds, since ytterbium-doped fibers provide optical-to-optical efficiencies well above 80%, hence becoming the first choice among the rare-earth ion-doped fibers ^[18]. Here researchers take ytterbium-doped MOFs as a clue and briefly introduce their application in laser amplification.

In fibers, the confinement of the light in a small core results in large intensities interacting with the material over long lengths, which triggers detrimental nonlinear effects. The amplification of ultrashort pulses directly in single-mode fibers is susceptible to the huge influence of nonlinear effects (self-phase modulation, stimulated Raman scattering (SRS), etc.), which leads to pulse distortion. In 2003, Limpert et al. constructed a chirped pulse amplification (CPA) system (schematic diagram illustrated in Figure 1) using Yb-doped double-clad fiber to reduce the peak power density in the core by several orders of magnitude to reduce the nonlinear effects. The final output with 76 W average power and 400 fs pulse width at 75 MHz repetition rate is obtained ^[19]. The oscillator is a 144 fs Nd:glass laser with a center wavelength of 1060 nm. The large mode area (LMA) of the ytterbium-doped fiber for the second-stage amplification is 415 μm², which is the key to realizing the transmission of femtosecond pulses with tolerable peak power density.

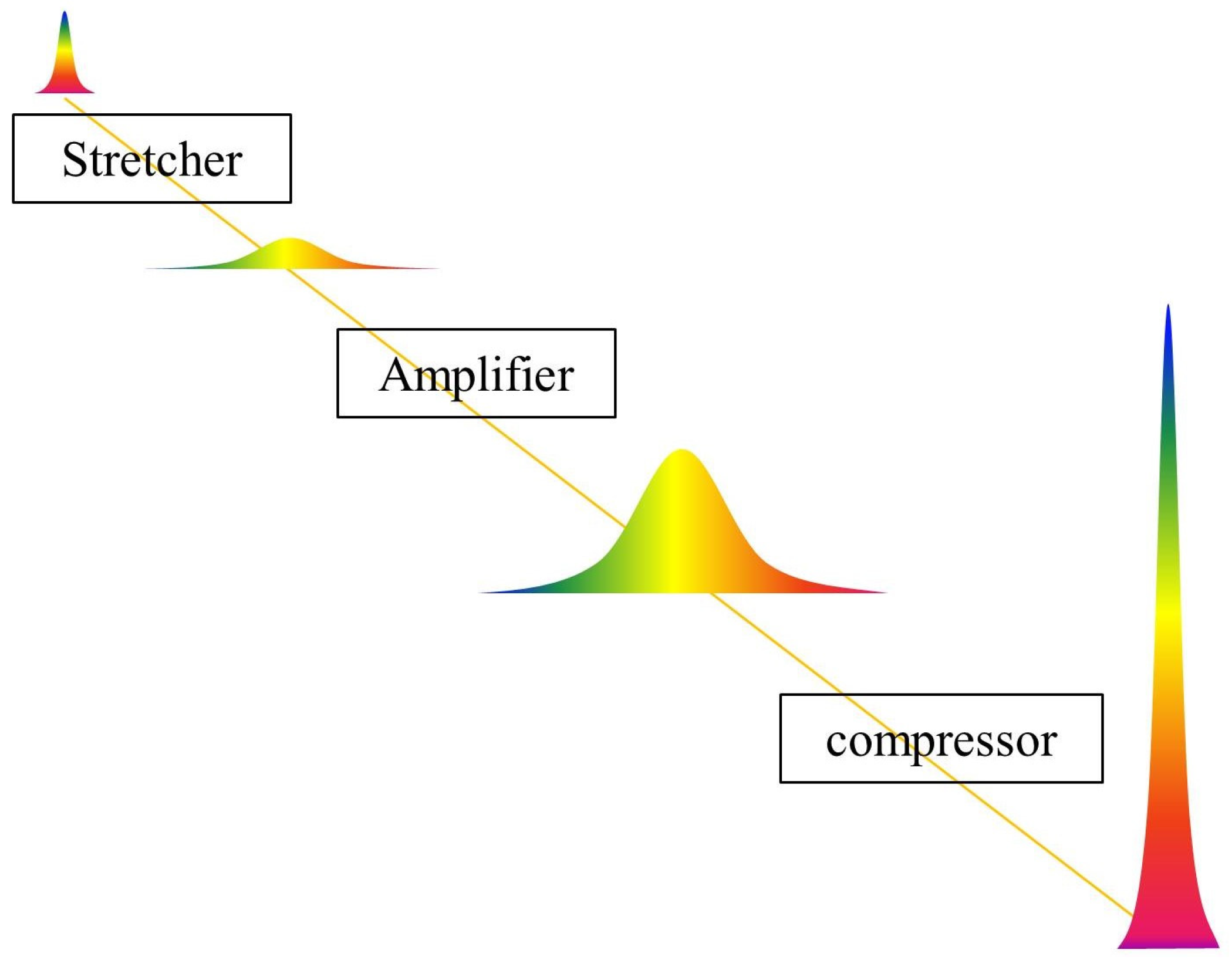
Figure 1. Schematic diagram of CPA technology.

Two years later, Limpert et al. designed Yb-doped rod-type PCFs, which are capable of providing high power extraction at short fiber lengths, solving the thermo-optic problem of coating damage. Due to the microstructure design of the PCF, it can output beam quality close to the diffraction limit. An output of 120 W with a center wavelength of 1035 nm was achieved, and the extracted power was 250 W/m; this was the highest value ever reported for fiber lasers at that time ^[20]. Subsequently, Röser et al. utilized Yb-doped rod-type PCF to build a CPA system with 100 W average power, 1 mJ pulse energy (the highest pulse energies ever reported from a fiber-based ultrafast laser system at that time), and an 800 fs pulse width. The first stage was a 1.2 m long air-clad PCF amplifier, and the second stage employed a 1.2 m long low-nonlinearity air-cladding rod-type PCF ^[21]. With the development of semiconductor lasers and PCF fabrication processes, higher output power was realized in an all-fiber system. Eidam et al. achieved 830 W average power by using a Yb-doped fiber CPA system, generating 640 fs pulse duration at a 78 MHz repetition rate ^[22]. The first stage of amplification consisted of a 1.2 m and 1.5 m Yb-doped double-clad PCF with a 30 μm core mode field and a 170 μm cladding mode field. The power output from the first stage could reach 100 W but was limited to 50 W to avoid the thermal lens effect in optical Faraday isolators. The main amplifier’s fiber was a water-cooled 8 m-long double-clad fiber with a 27 μm mode field diameter and 500 μm air clad.

Wan et al. constructed two kinds of all-fiber systems: Yb-doped high-energy and high-power femtosecond fiber lasers, respectively ^[23]. High energy system output: 1 mJ pulses at 100 kHz and 705 fs pulse duration; high power system output: 1052 W average power at 69 MHz and 800 fs pulse duration. The high energy system employed a Yb-doped ultra-large-core single-mode rod PCF seeded with a 50 µJ chirped pulse fiber laser. The high power system’s active medium was an 8 m-long double-cladding LMA fiber with a core diameter of 30 µm. However, continuing to increase the power of fiber lasers is limited by mode instability and excessive nonlinearity. In order to avoid these limitations, Müller et al. built an ultrafast fiber CPA system comprising eight coherently combined amplifier channels, boosting the average power to 1000 W with 1 mJ pulse energy and 260 fs pulse duration by employing large-pitch fibers (LPFs) with mode-field diameters as large as 64 μm ^[24]. Further, Stark et al. built a coherently combined Yb-doped LPF CPA laser system that outputs 1000 W average power with 10 mJ pulse energy and 120 fs pulses ^[25] (as shown in Figure 2). In 2023, Stark et al. boosted the data to 32 mJ and 158 fs at a 20 kHz repetition rate with an average power of 640 W, which was achieved by 16 parallel Yb-doped rod-type amplifiers ^[26]. It is worth pointing out that the output power of fiber lasers can reach more than 10,000 W through similar coherent combined amplification ^[27].

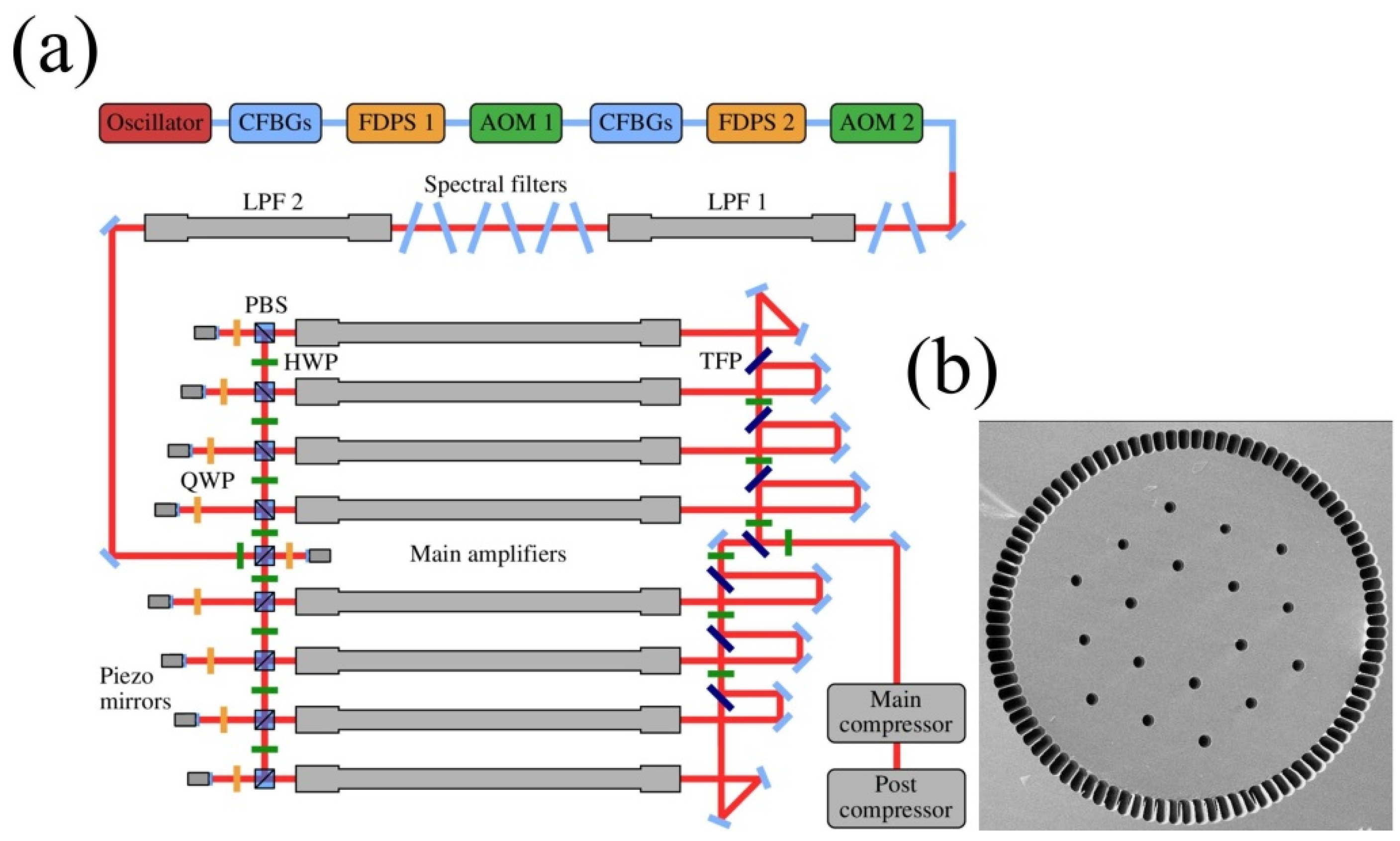
Figure 2. (a) Schematic of the coherently combined fiber CPA laser system (CFBG, chirped fiber Bragg gratings; FDPS, Fourier-domain pulse shaper; AOM, acousto-optic modulator; LPF, large-pitch fiber; QWP, quarter-wave plate; HWP, half-wave plate; PBS, polarizing beam splitter; TFP, thin-film polarizer); (b) SEM image of the cross-section of the LPF (the core diameter is 135 μm).

2.2. Spectrum Engineering

MOFs have been used in numerous works for spectral engineering, and their versatile structure allows different nonlinearities and dispersions to be met, which has enabled the realization of many ideas in spectrum modulation.

2.2.1. Supercontinuum Generation

The pursuit of the generation of different wavelengths of light has been ceaseless; different wavelengths of light have their own applications, and the emergence of supercontinuum has opened up a new perspective. SCG is undoubtedly one of the most successful applications of PCF. The generation of supercontinuum (SC) is achieved by the use of narrowband pulses incident on a nonlinear medium, resulting in a significant broadening of the spectrum. Compact SC sources are indispensable in many optical laboratories. The SCG was observed for the first time in 1970 when Alfano et al. launched picosecond pulses into a bulk optical crystal ^[28]. The emergence of the PCF provides an excellent nonlinear guiding medium for SCG with manageable nonlinearity and zero-dispersion wavelengths (ZDW) ^[29], enabling very strong spectrum broadening with a low-power pumping source such as a high-repetition-rate femtosecond laser resonator. In 1999, Ranka et al. demonstrated experimentally for the first time a broadband spectrum spanning from UV to NIR generated in a PCF with ZDW around 780 nm when pumped by 100 fs, 790 nm pulses with a peak power of kilowatts ^[30]. Subsequently, there has been a lot of research on PCFs to generate SC light, and the mechanisms and mathematical models have been intensively investigated ^[31]^[32]. Birks et al. pumped a tapered fiber with 200 fs, 3.9 nJ pulses from a Ti:sapphire laser, producing a broad spectrum from 400 nm to nearly 1600 nm ^[33]. Genty et al. used a 5 m long PCF with a highly birefringent elliptical core, produced a SC spectrum from 400 nm to beyond 1400 nm, and found that the experiments agreed well with their theories. The pump source was a Ti:sapphire laser with 100 fs pulse duration, 80 MHz repetition, and 1.7 W average power ^[34]. At the beginning of the 21st century, a lot of work was conducted by pumping PCFs with different experimental conditions (e.g., different pulse conditions or different structures of PCFs) to study the nonlinear and dispersion mechanisms in SCG ^[35]^[36]^[37]. It is worth pointing out that these PCFs are mostly solid and based on the refractive index guidance.

Extension of the spectrum to the UV direction was carried out by various methods, including the use of cascaded PCFs, tapered PCFs, nanoscale fibers, etc. Stone and Knight from Bath University obtained a spectrum from 350 nm up to 2450 nm, 50 nm deeper into the short-wave direction than the previous works, by modifying the structure of the PCF (see Figure 3) when pumped by a microchip laser with a pulse width of 600 ps at 1064 nm ^[38]. Chen et al. pumped 700 ps pulses at 1064 nm into a system consisting of three tapered PCFs in cascade to produce a SC spectrum spanning from 352 nm to 1750 nm ^[39]. Stark et al. used 800 nm, 130 fs, and 2 nJ pulses to pump a tapered solid core PCF to produce a SC spectrum down to 280 nm and found that the deep-UV radiation is limited by strong two-photon absorption in silica ^[40].

In terms of a high-power SC source, Qi et al. pumped 120 ps pulses at 1016 nm into a multi-core PCF, which was designed to provide strong dispersion to satisfy the conditions for UV SCG. The system outputs an 80 W SC light from 350 to 2400 nm ^[41]. Zhang et al. made an all-fiber SCG system using 1064 nm picosecond pulses pumped cascade PCF to obtain 104 W SC output covering 370 nm to 2400 nm ^[42]. It is difficult for a solid-core PCF to produce light at deeper UV. Ermolov et al. overcame this limitation by introducing a He-filled HC-kagome-style PCF. They launched linearly polarized, 35 fs, 1 kHz pulses at 800 nm generated by a Ti:sapphire amplifier into the He-filled HC-PCF and produced a SC covering 113 nm vacuum ultraviolet to 1000 nm NIR ^[43], where the key point is that the ZDW of the HC-PCF is in the UV region.

Figure 3. Experimental spectra of SCG. The blue curve was measured by the VUV spectrometer, and the brown curve was UV-NIR spectrometer. The solid black line is the simulated spectrum. The dashed vertical line marks the ZDW (N = normal, A = anomalous GVD).

Silica fibers limit the extension of SCG in the IR region to the vicinity of 2 μm due to the transmittance range. Researchers have gradually adopted other highly nonlinear materials for manufacturing PCF as the medium for SCG, such as tellurite, fluoride, chalcogenide (ChG), etc., which have a longer transparent edge in IR and can be well used as the medium for IR SCG. Delmonte et al. used a femtosecond OPO output of 1.5 μm to pump a tellurite wagon wheel MOF to produce a SC from 0.9 to 2.5 μm ^[44]. Domachuk et al. launched 1550 nm, 100 fs pulses into a section of a highly nonlinear tellurite microstructured PCF to produce SC extending from 789 nm to 4870 nm, which occurs in a sub-cm (8 mm) length of this PCF ^[45].

Among several types of promoting mid-IR optical glasses, optical fibers made of selenides and sulfides are extremely fragile, and toxic compounds are added to improve nonlinearity, whereas these problems can be avoided by using heavy metal oxide glasses. Buczynski et al. pumped 1540 nm, 150 fs pulses into a single-mode PCF made of lead-bismuth-gallate glass, producing a SC spectrum from 700 nm to 3000 nm ^[46], which was the broadest SC reported in heavy metal oxide glass fibers at that time.

ChG has an extremely wide transparency window (over 20 μm) and high nonlinearity (up to a thousand times greater than that of silica glasses), which make it one of the outstanding candidates for mid-IR SCG. Liu et al. obtained 2.2~3.3 μm SC from an all-solid ChG MOF with all-normal dispersion. The pump is an OPO output pulse with 2.7 μm, 200 fs, and 80 MHz ^[47]. Wang et al. pumped ChG step-index tapered fibers with 3.25 μm, 150 fs pulses in the normal dispersion regime and obtained a SC from 1.4 μm to 7.2 μm ^[48]. Xing et al. obtained a SC from 1670 nm to 2880 nm by pumping ChG PCF with pulses of 79 fs, 2070 nm, and 2.9 kW peak power. Their simulation by utilizing the generalized nonlinear Schrodinger equation model was in agreement with the experimental results ^[49].

Moreover, Tarnowski et al. reported a very compact all-fiber SC source (see Figure 4). By pumping the 25 fs, 116 mW pulses from Er-doped fiber into an all-normal dispersion MOF, a SC from 1.1 to 2.2 μm was obtained ^[50], which is simple and opens the path to outside-lab applications of SCG. In 2021, Zhu et al. used a dual-band MOPA system (1 μm and 1.5 μm) to pump a cascaded PCF to generate a 500~3000 nm SC with a maximum output power of 9 W ^[51]. Which is the highest power ever achieved from a SC source spanning from the visible to mid-infrared at that time.

Figure 4. Experimental setup of the compact SC source (EDF: Erbium-doped fiber; GSA: graphene saturable absorber; OC: output coupler; ISO: isolator; WDM: wavelength division multiplexer; PM-HNLF: polarization maintaining highly nonlinear fiber).

2.2.2. UV Generation

Ultrafast UV lasers have significant value in many applications due to their unique properties. Short-wavelength light has a smaller focusing area and higher photon energy, which are important in fields such as attosecond science ^[9], photolithography ^[52], etc. Ultrafast UV generation can be sorted by mechanisms, such as high harmonic generation (HHG) ^[53]^[54], third harmonic generation of NIR ^[55]^[56], filtering out the UV portion of the SCG, dispersive wave emission ^[57], and so on. Researchers take the gas-filled HC-PCF as a clue to illustrate its application for UV generation in terms of HHG and dispersive wave emission. Using gas-filled HC-PCF to generate ultrafast UV lasers can eliminate the diffraction of light in gases so that the UV output has excellent beam quality. Moreover, HC-PCF has high UV transparency and is less susceptible to material damage than solid materials.

HHG can produce very short wavelength output in extreme UV or even soft X-ray regions, and the mechanism can be explained by the three-step model ^[58]. Conventionally, intense infrared laser pulses are tightly focused into a noble gas jet to obtain HHG, which restricts the interaction length to the Rayleigh range of the focus. Utilizing a gas-filled HC-PCF to generate HHG can increase the interaction distance and obtain excellent conversion efficiency at low-energy pulses. In 2009, Heckl et al. first obtained HHG up to the 13th harmonic in a 15 mm-long kagome-type HC-PCF filled with Xe (see Figure 5). The system was pumped by an 800 nm, 10 μJ, 30 fs, 1 kHz Ti:sapphire laser, implying a UV wavelength that reaches near 50 nm ^[59], but the conversion efficiency was very low (10⁻⁹). Imperfect phase-matching leads to a significant reduction in the efficiency of HHG. Wiegandt et al. developed a time-multiplexed multimodal quasi-phase-matching technique that can solve the problem of efficiency. They used a negative-curvature PCF filled with Ne to obtain HHG up to 39th when pumped by pulses of 30 fs and 15 μJ at 790 nm, implying a high harmonic wavelength down to 20 nm, photon energy up to 61.6 eV, and a 60-fold enhancement of the HHG flux ^[60]. Tani et al. combined a gas-filled HC-PCF with a gas jet for HHG driven by laser pulses of a few tens of microjoules and obtained an output tunable from 17 to 45 eV ^[61].

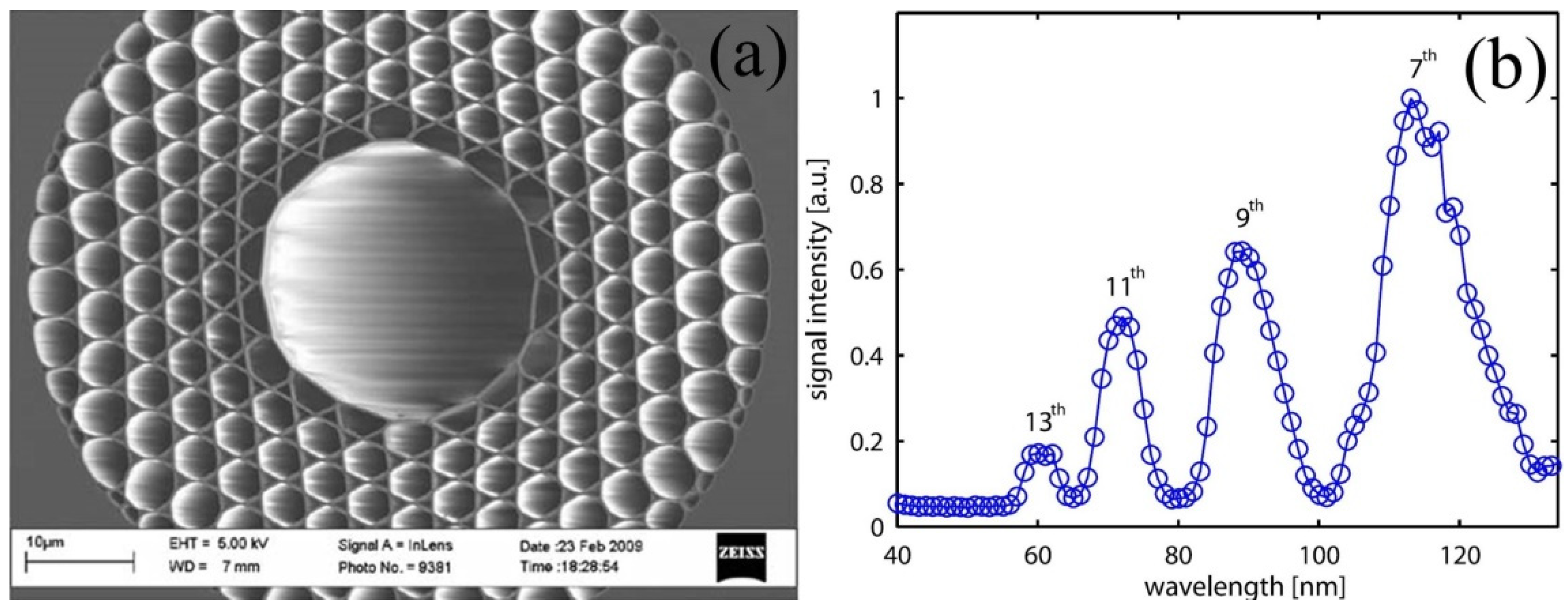
Figure 5. (a) SEM image of the cross section of the kagome-type HC-PCF used for HHG, where the effective mode diameter (corresponding to the hollow center core) is about 15 μm; (b) Measured spectrum of the HHG.

The UV generation from filtered SCG in a solid-core PCF has low brightness and is limited to 280 nm ^[40]. In contrast, the UV generated by the dispersive wave mechanism of a gas-filled HC-PCF can concentrate the energy into a narrower bandwidth, which is an excellent method to obtain a tunable UV output. The dispersive wave emission originates from the fundamental soliton propagation perturbed by high-order dispersion ^[62]. Joly et al. utilized 800 nm, 30 fs, and 1 μJ pulses to pump an Ar-filled HC-PCF and generate 200~320 nm tunable UV light. The wavelength tuning was achieved by varying the pulse energy, gas pressure, and IR to UV conversion efficiencies of up to 8%, with a threshold as low as 290 nJ ^[63]. Mak et al. conducted further study by pumping a HC-PCF filled with different gases using a light source of 800 nm and obtained a tunable output from 176 nm to 550 nm (see Figure 6). They also carried out numerical simulations, which were in good agreement with the experimental results ^[64].

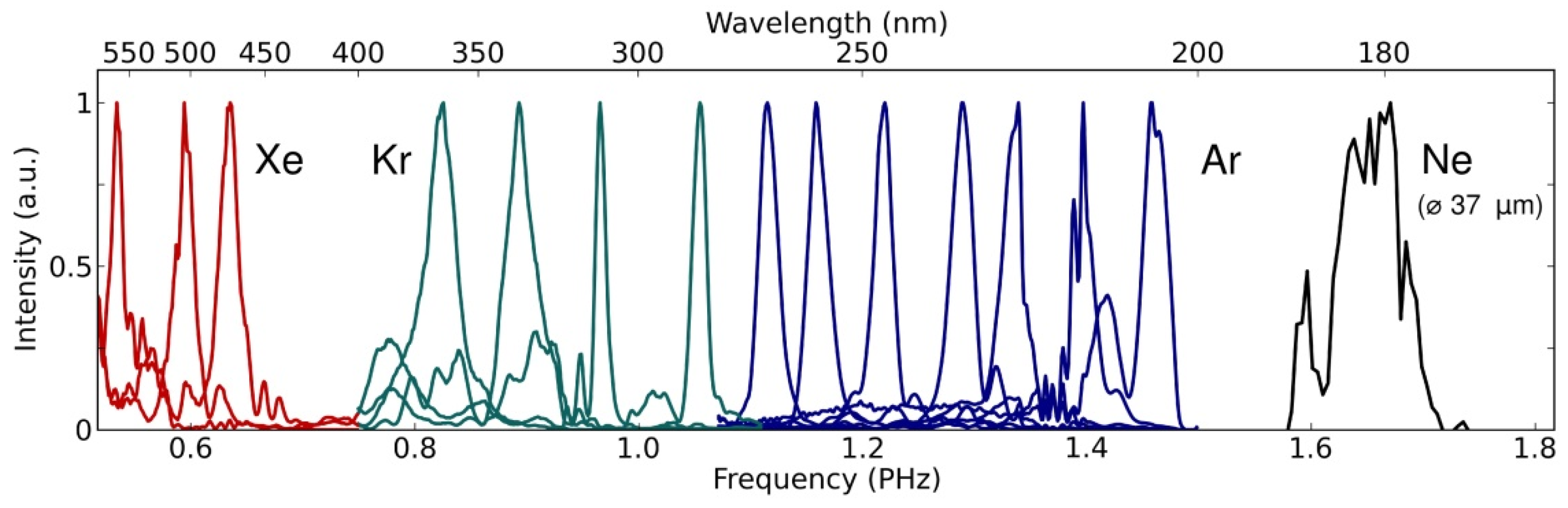
Figure 6. Experimental generation of coherent ultrashort pulses through resonant dispersive wave emission in gas-filled kagome HC-PCF. Each peak is the individual normalized spectrum for a specific gas, pressure, and pump energy. All the tuning was carried out in an identical length of kagomé HC-PCF (27 µm core diameter), except in the case of neon, where the core diameter was 37 µm.

Lowering the pumping energy threshold for obtaining UV output is desired. Recently, Sabbah et al. utilized an Ar-filled ARF with a core diameter of just 6 µm, which is much smaller than previous studies, and obtained a 220~700 nm spectrum with an input pulse energy of as low as 50 nJ ^[65]. While dispersive waves are usually used as a means of generating UV light, Meng et al. obtained additional NIR output, along with the 267~460 nm spectrum, by pumping a 42 cm-long Ar-filled kagome PCF with pulses of 40 fs at 1 μm and interpreting it with a more accurate antiresonant tube model ^[66].

2.2.3. IR Generation

Raman soliton self-frequency shift (SSFS) is one of the most effective methods to extend the wavelength to a longer region. It is the redshift of the wavelength of a high-peak power pulse under the effect of stimulated Raman scattering when it is transmitted in a nonlinear medium with anomalous dispersion. SSFS generates continuously tunable femtosecond pulses with a relatively concentrated spectrum, avoiding the utilization of extra nonlinear frequency conversion efforts such as optical parametric oscillators. There has been a lot of research on the SSFS since the emergence of PCF. Washburn et al. used a 110 fs, 806 nm Ti:sapphire laser-pumped 1.7 m PCF to produce Raman solitons tunable from 850 nm to 1050 nm ^[67]. Liu et al. launched 200 fs, 1.3 μm, 80 MHz pulses into a tapered air-silica MOF and obtained soliton pulses tunable in the range of 1.3 μm to 1.65 μm with a compressed pulse duration of less than 100 fs ^[68]. Nishizawa et al. used a 780 nm frequency-doubled Er-doped fiber laser to pump a 60 cm PCF and produced femtosecond tunable soliton pulses in the range of 780 nm to 900 nm ^[69]. A shorter pulse width benefits the SFSS effect greatly. Ishii et al. shifted a 6 fs Ti:sapphire laser pulse from 800 nm to 1.35 μm continuously by the SSFS effect in the PCF ^[70]. Using a highly nonlinear PCF, Chan et al. produced a 1245~2160 nm tunable output, and the range has reached the upper boundary of silica material, with pump pulses of 65 fs at 1245 nm ^[71].

OH absorption is a limiting factor in the SSFS when pumping below 1380 nm. Dekker et al. designed a PCF with reduced OH loss and produced a tunable output over more than an octave from 801 nm to 1708 nm ^[72]. Yuan et al. purified the silica material of PCF by the complex method of rectification and adsorption, greatly reduced the contents of OH, metal ions, and metallic and non-metallic oxides, and then obtained soliton pulses above 2 μm with a tuning range of 300 nm when coupled at 870 nm into a highly birefringent PCF ^[73]. While many fibers for SSFS are designed for only one wavelength, Szewczyk et al. designed a highly birefringent MOF that can be applied to SSFS at both 1.04 μm and 1.55 μm. With 1.04 μm pumping, the soliton pulses can be continuously tuned from 1.04 μm to 1.67 μm, and with 1.55 μm pumping, the pulse can be continuously tuned from 1.55 μm to 1.95 μm ^[74]. This has promising applications in multiphoton imaging and other areas.

The absorption loss of silica limits the SSFSs ability to achieve wavelengths longer than 2 μm. However, light sources above 2 μm are in the eye-safe range and have important applications, such as medical treatment. Bi et al., using a tellurite MOF, obtained the wavelength shift range from 1990 nm to 2264 nm by merely varying the pump power of a Tm-doped mode-locked fiber laser with a pulse width of 2.9 ps and a center wavelength near 2 μm ^[75]. Alamgir et al. employed an 8 cm highly nonlinear As₂S₃ tapered suspended core MOF for achieving tunable outputs from 2.04 μm to 2.66 μm ^[76].

References

Siek, F.; Neb, S.; Bartz, P.; Hensen, M.; Strüber, C.; Fiechter, S.; Torrent-Sucarrat, M.; Silkin, V.M.; Krasovskii, E.E.; Kabachnik, N.M. Angular momentum–induced delays in solid-state photoemission enhanced by intra-atomic interactions. Science 2017, 357, 1274–1277.
Géneaux, R.; Kaplan, C.J.; Yue, L.; Ross, A.D.; Bækhøj, J.E.; Kraus, P.M.; Chang, H.-T.; Guggenmos, A.; Huang, M.-Y.; Zürch, M. Attosecond time-domain measurement of core-level-exciton decay in magnesium oxide. Phys. Rev. Lett. 2020, 124, 207401.
Calegari, F.; Ayuso, D.; Trabattoni, A.; Belshaw, L.; De Camillis, S.; Anumula, S.; Frassetto, F.; Poletto, L.; Palacios, A.; Decleva, P. Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses. Science 2014, 346, 336–339.
Mara, M.W.; Hadt, R.G.; Reinhard, M.E.; Kroll, T.; Lim, H.; Hartsock, R.W.; Alonso-Mori, R.; Chollet, M.; Glownia, J.M.; Nelson, S. Metalloprotein entatic control of ligand-metal bonds quantified by ultrafast X-ray spectroscopy. Science 2017, 356, 1276–1280.
Sansone, G.; Kelkensberg, F.; Pérez-Torres, J.; Morales, F.; Kling, M.F.; Siu, W.; Ghafur, O.; Johnsson, P.; Swoboda, M.; Benedetti, E. Electron localization following attosecond molecular photoionization. Nature 2010, 465, 763–766.
Scherer, N.; Knee, J.; Smith, D.; Zewail, A. Femtosecond photofragment spectroscopy: The reaction ICN→CN + I. J. Phys. Chem. 1985, 89, 5141–5143.
McClung, F.J.; Hellwarth, R.W. Giant optical pulsations from ruby. Appl. Opt. 1962, 1, 103–105.
Fork, R.; Greene, B.; Shank, C.V. Generation of optical pulses shorter than 0.1 psec by colliding pulse mode locking. Appl. Phys. Lett. 1981, 38, 671–672.
Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513.
Strycker, B.D.; Han, Z.; Commer, B.; Shaw, B.D.; Sokolov, A.V.; Scully, M.O. CARS spectroscopy of Aspergillus nidulans spores. Sci. Rep. 2019, 9, 1789.
Lee, J.H.; Cho, E.H.; Shin, S.-M.; Oh, M.-K.; Ko, D.-K. Comparative study of breast normal and cancer cells using coherent anti-Stokes Raman scattering microspectroscopy imaging. Appl. Phys. Express 2012, 5, 082401.
Kurokawa, K.; Tajima, K.; Nakajima, K. 10-GHz 0.5-ps pulse generation in 1000-nm band in PCF for high-speed optical communication. J. Light. Technol. 2007, 25, 75–78.
Schibli, T.; Hartl, I.; Yost, D.; Martin, M.; Marcinkevičius, A.; Fermann, M.; Ye, J. Optical frequency comb with submillihertz linewidth and more than 10 W average power. Nat. Photonics 2008, 2, 355–359.
Zhu, W.; Yi, Y.; Yi, Z.; Bian, L.; Yang, H.; Zhang, J.; Yu, Y.; Liu, C.; Li, G.; Wu, X. High confidence plasmonic sensor based on photonic crystal fibers with a U-shaped detection channel. Phys. Chem. Chem. Phys. 2023, 25, 8583–8591.
Wang, D.; Zhu, W.; Yi, Z.; Ma, G.; Gao, X.; Dai, B.; Yu, Y.; Zhou, G.; Wu, P.; Liu, C. Highly sensitive sensing of a magnetic field and temperature based on two open ring channels SPR-PCF. Opt. Express 2022, 30, 39055–39067.
Jing, J.; Liu, K.; Jiang, J.; Xu, T.; Wang, S.; Liu, T. Highly sensitive and stable probe refractometer based on configurable plasmonic resonance with nano-modified fiber core. Opto-Electron. Adv. 2023, 6, 220072-1–220072-14.
Yang, L.; Li, Y.; Fang, F.; Li, L.; Yan, Z.; Zhang, L.; Sun, Q. Highly sensitive and miniature microfiber-based ultrasound sensor for photoacoustic tomography. Opto-Electron. Adv. 2022, 5, 200076-1–200076-8.
Paschotta, R.; Nilsson, J.; Tropper, A.C.; Hanna, D.C. Ytterbium-doped fiber amplifiers. IEEE J. Quantum Electron. 1997, 33, 1049–1056.
Limpert, J.; Clausnitzer, T.; Liem, A.; Schreiber, T.; Fuchs, H.-J.; Zellmer, H.; Kley, E.-B.; Tnnermann, A. High-average-power femtosecond fiber chirped-pulse amplification system. Opt. Lett. 2003, 28, 1984–1986.
Limpert, J.; Deguil-Robin, N.; Manek-Hönninger, I.; Salin, F.; Röser, F.; Liem, A.; Schreiber, T.; Nolte, S.; Zellmer, H.; Tünnermann, A. High-power rod-type photonic crystal fiber laser. Opt. Express 2005, 13, 1055–1058.
Röser, F.; Eidam, T.; Rothhardt, J.; Schmidt, O.; Schimpf, D.; Limpert, J.; Tünnermann, A. Millijoule pulse energy high repetition rate femtosecond fiber chirped-pulse amplification system. Opt. Lett. 2007, 32, 3495–3497.
Eidam, T.; Hanf, S.; Seise, E.; Andersen, T.V.; Gabler, T.; Wirth, C.; Schreiber, T.; Limpert, J.; Tünnermann, A. Femtosecond fiber CPA system emitting 830 W average output power. Opt. Lett. 2010, 35, 94–96.
Wan, P.; Yang, L.-M.; Liu, J. All fiber-based Yb-doped high energy, high power femtosecond fiber lasers. Opt. Express 2013, 21, 29854–29859.
Müller, M.; Kienel, M.; Klenke, A.; Gottschall, T.; Shestaev, E.; Plötner, M.; Limpert, J.; Tünnermann, A. 1 kW 1 mJ eight-channel ultrafast fiber laser. Opt. Lett. 2016, 41, 3439–3442.
Stark, H.; Buldt, J.; Müller, M.; Klenke, A.; Limpert, J. 1 kW, 10 mJ, 120 fs coherently combined fiber CPA laser system. Opt. Lett. 2021, 46, 969–972.
Stark, H.; Benner, M.; Buldt, J.; Klenke, A.; Limpert, J. Pulses of 32 mJ and 158 fs at 20-kHz repetition rate from a spatiotemporally combined fiber laser system. Opt. Lett. 2023, 48, 3007–3010.
Müller, M.; Aleshire, C.; Klenke, A.; Haddad, E.; Légaré, F.; Tünnermann, A.; Limpert, J. 10.4 kW coherently combined ultrafast fiber laser. Opt. Lett. 2020, 45, 3083–3086.
Alfano, R.; Shapiro, S. Emission in the region 4000 to 7000 Å via four-photon coupling in glass. Phys. Rev. Lett. 1970, 24, 584.
Knight, J.; Arriaga, J.; Birks, T.; Ortigosa-Blanch, A.; Wadsworth, W.; Russell, P.S.J. Anomalous dispersion in photonic crystal fiber. IEEE Photonics Technol. Lett. 2000, 12, 807–809.
Ranka, J.K.; Windeler, R.S.; Stentz, A.J. Visible continuum generation in air–silica microstructure optical fibers with anomalous dispersion at 800 nm. Opt. Lett. 2000, 25, 25–27.
Husakou, A.; Herrmann, J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 2001, 87, 203901.
Husakou, A.V.; Herrmann, J. Supercontinuum generation, four-wave mixing, and fission of higher-order solitons in photonic-crystal fibers. JOSA B 2002, 19, 2171–2182.
Birks, T.; Wadsworth, W.; Russell, P.S.J. Supercontinuum generation in tapered fibers. Opt. Lett. 2000, 25, 1415–1417.
Genty, G.; Lehtonen, M.; Ludvigsen, H.; Broeng, J.; Kaivola, M. Spectral broadening of femtosecond pulses into continuum radiation in microstructured fibers. Opt. Express 2002, 10, 1083–1098.
Coen, S.; Chau, A.H.L.; Leonhardt, R.; Harvey, J.D.; Knight, J.C.; Wadsworth, W.J.; Russell, P.S.J. Supercontinuum generation by stimulated Raman scattering and parametric four-wave mixing in photonic crystal fibers. JOSA B 2002, 19, 753–764.
Sakamaki, K.; Nakao, M.; Naganuma, M.; Izutsu, M. Soliton induced supercontinuum generation in photonic crystal fiber. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 876–884.
Genty, G.; Lehtonen, M.; Ludvigsen, H.; Kaivola, M. Enhanced bandwidth of supercontinuum generated in microstructured fibers. Opt. Express 2004, 12, 3471–3480.
Stone, J.M.; Knight, J.C. Visibly “white” light generation in uniform photonic crystal fiber using a microchip laser. Opt. Express 2008, 16, 2670–2675.
Chen, H.; Chen, Z.; Zhou, X.; Hou, J. Ultraviolet-extended flat supercontinuum generation in cascaded photonic crystal fiber tapers. Laser Phys. Lett. 2013, 10, 085401.
Stark, S.; Travers, J.; Russell, P.S.J. Extreme supercontinuum generation to the deep UV. Opt. Lett. 2012, 37, 770–772.
Qi, X.; Chen, S.; Li, Z.; Liu, T.; Ou, Y.; Wang, N.; Hou, J. High-power visible-enhanced all-fiber supercontinuum generation in a seven-core photonic crystal fiber pumped at 1016 nm. Opt. Lett. 2018, 43, 1019–1022.
Zhang, H.; Li, Y.; Yan, D.; Dong, K.; Lin, H.; Wang, J.; Jing, F. All-fiber high power supercontinuum generation by cascaded photonic crystal fibers ranging from 370 nm to 2400 nm. IEEE Photonics J. 2020, 12, 1–8.
Ermolov, A.; Mak, K.F.; Frosz, M.H.; Travers, J.C.; Russell, P.S.J. Supercontinuum generation in the vacuum ultraviolet through dispersive-wave and soliton-plasma interaction in a noble-gas-filled hollow-core photonic crystal fiber. Phys. Rev. A 2015, 92, 033821.
Delmonte, T.; Watson, M.A.; O’Driscoll, E.J.; Feng, X.; Monro, T.M.; Finazzi, V.; Petropoulos, P.; Price, J.H.; Baggett, J.C.; Loh, W. Generation of mid-IR continuum using tellurite microstructured fiber. In Proceedings of the 2006 Conference on Lasers and Electro-Optics and 2006 Quantum Electronics and Laser Science Conference, Long Beach, CA, USA, 21–26 May 2006; pp. 1–2.
Domachuk, P.; Wolchover, N.; Cronin-Golomb, M.; Wang, A.; George, A.K.; Cordeiro, C.; Knight, J.C.; Omenetto, F. Over 4000 nm bandwidth of mid-IR supercontinuum generation in sub-centimeter segments of highly nonlinear tellurite PCFs. Opt. Express 2008, 16, 7161–7168.
Buczynski, R.; Bookey, H.; Klimczak, M.; Pysz, D.; Stepien, R.; Martynkien, T.; McCarthy, J.E.; Waddie, A.J.; Kar, A.K.; Taghizadeh, M.R. Two octaves supercontinuum generation in lead-bismuth glass based photonic crystal fiber. Materials 2014, 7, 4658–4668.
Liu, L.; Cheng, T.; Nagasaka, K.; Tong, H.; Qin, G.; Suzuki, T.; Ohishi, Y. Coherent mid-infrared supercontinuum generation in all-solid chalcogenide microstructured fibers with all-normal dispersion. Opt. Lett. 2016, 41, 392–395.
Wang, Y.; Dai, S.; Li, G.; Xu, D.; You, C.; Han, X.; Zhang, P.; Wang, X.; Xu, P. 1.4–7.2 μm broadband supercontinuum generation in an As-S chalcogenide tapered fiber pumped in the normal dispersion regime. Opt. Lett. 2017, 42, 3458–3461.
Xing, S.; Kharitonov, S.; Hu, J.; Brès, C.-S. Linearly chirped mid-infrared supercontinuum in all-normal-dispersion chalcogenide photonic crystal fibers. Opt. Express 2018, 26, 19627–19636.
Tarnowski, K.; Martynkien, T.; Mergo, P.; Sotor, J.; Soboń, G. Compact all-fiber source of coherent linearly polarized octave-spanning supercontinuum based on normal dispersion silica fiber. Sci. Rep. 2019, 9, 12313.
Zhu, Y.; Zheng, Z.; Ge, X.; Du, G.; Ruan, S.; Guo, C.; Yan, P.; Hua, P.; Xia, L.; Lü, Q. High-power, ultra-broadband supercontinuum source based upon 1/1.5 µm dual-band pumping. Chin. Opt. Lett. 2021, 19, 041403.
Naulleau, P.; Goldberg, K.A.; Anderson, E.H.; Bradley, K.; Delano, R.; Denham, P.; Gunion, B.; Harteneck, B.; Hoef, B.; Huang, H. Status of EUV micro-exposure capabilities at the ALS using the 0.3-NA MET optic. In Proceedings of the Emerging Lithographic Technologies VIII, Santa Clara, CA, USA, 24–26 February 2004; pp. 881–891.
Ferray, M.; L’Huillier, A.; Li, X.; Lompre, L.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B At. Mol. Opt. Phys. 1988, 21, L31.
L’Huillier, A.; Schafer, K.; Kulander, K. Higher-order harmonic generation in xenon at 1064 nm: The role of phase matching. Phys. Rev. Lett. 1991, 66, 2200.
Rines, G.; Zenzie, H.; Schwarz, R.; Isyanova, Y.; Moulton, P. Nonlinear conversion of Ti: Sapphire laser wavelengths. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 50–57.
Rothhardt, J.; Rothhardt, C.; Müller, M.; Klenke, A.; Kienel, M.; Demmler, S.; Elsmann, T.; Rothhardt, M.; Limpert, J.; Tünnermann, A. 100 W average power femtosecond laser at 343 nm. Opt. Lett. 2016, 41, 1885–1888.
Cristiani, I.; Tediosi, R.; Tartara, L.; Degiorgio, V. Dispersive wave generation by solitons in microstructured optical fibers. Opt. Express 2004, 12, 124–135.
Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994.
Heckl, O.; Baer, C.; Kränkel, C.; Marchese, S.; Schapper, F.; Holler, M.; Südmeyer, T.; Robinson, J.; Tisch, J.; Couny, F. High harmonic generation in a gas-filled hollow-core photonic crystal fiber. Appl. Phys. B 2009, 97, 369–373.
Wiegandt, F.; Anderson, P.N.; Yu, F.; Treacher, D.J.; Lloyd, D.T.; Mosley, P.J.; Hooker, S.M.; Walmsley, I.A. Quasi-phase-matched high-harmonic generation in gas-filled hollow-core photonic crystal fiber. Optica 2019, 6, 442–447.
Tani, F.; Frosz, M.H.; Travers, J.C.; Russell, P.S.J. Continuously wavelength-tunable high harmonic generation via soliton dynamics. Opt. Lett. 2017, 42, 1768–1771.
Austin, D.R.; de Sterke, C.M.; Eggleton, B.J.; Brown, T.G. Dispersive wave blue-shift in supercontinuum generation. Opt. Express 2006, 14, 11997–12007.
Joly, N.Y.; Nold, J.; Chang, W.; Hölzer, P.; Nazarkin, A.; Wong, G.; Biancalana, F.; Russell, P.S.J. Bright spatially coherent wavelength-tunable deep-UV laser source using an Ar-filled photonic crystal fiber. Phys. Rev. Lett. 2011, 106, 203901.
Mak, K.F.; Travers, J.C.; Hölzer, P.; Joly, N.Y.; Russell, P.S.J. Tunable vacuum-UV to visible ultrafast pulse source based on gas-filled Kagome-PCF. Opt. Express 2013, 21, 10942–10953.
Sabbah, M.; Harrington, K.; Mears, R.; Brahms, C.; Alisauskas, A.; Murphy, L.R.; Yerolatsitis, S.; Wadsworth, W.J.; Knight, J.C.; Stone, J.M. Low-Threshold Green-Pumped Ultraviolet Resonant Dispersive-Wave Emission in Small-Core Anti-Resonant Hollow-Fibre. In Proceedings of the 2023 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 26–30 June 2023; p. 1.
Meng, F.; Liu, B.; Wang, S.; Liu, J.; Li, Y.; Wang, C.; Zheltikov, A.; Hu, M. Controllable two-color dispersive wave generation in argon-filled hypocycloid-core kagome fiber. Opt. Express 2017, 25, 32972–32984.
Washburn, B.; Ralph, S.E.; Lacourt, P.A.; Dudley, J.; Rhodes, W.T.; Windeler, R.S.; Coen, S. Tunable near-infrared femtosecond soliton generation in photonic crystal fibres. Electron. Lett. 2001, 37, 1.
Liu, X.; Xu, C.; Knox, W.; Chandalia, J.; Eggleton, B.; Kosinski, S.; Windeler, R. Soliton self-frequency shift in a short tapered air–silica microstructure fiber. Opt. Lett. 2001, 26, 358–360.
Nishizawa, N.; Ito, Y.; Goto, T. 0.78–0.90-μm wavelength-tunable femtosecond soliton pulse generation using photonic crystal fiber. IEEE Photonics Technol. Lett. 2002, 14, 986–988.
Ishii, N.; Teisset, C.Y.; Köhler, S.; Serebryannikov, E.; Fuji, T.; Metzger, T.; Krausz, F.; Baltuška, A.; Zheltikov, A. Widely tunable soliton frequency shifting of few-cycle laser pulses. Phys. Rev. E 2006, 74, 036617.
Chan, M.-C.; Chia, S.-H.; Liu, T.-M.; Tsai, T.-H.; Ho, M.-C.; Ivanov, A.A.; Zheltikov, A.M.; Liu, J.-Y.; Liu, H.-L.; Sun, C.-K. 1.2-to 2.2-μm tunable Raman soliton source based on a Cr: Forsterite laser and a photonic-crystal fiber. IEEE Photonics Technol. Lett. 2008, 20, 900–902.
Dekker, S.A.; Judge, A.C.; Pant, R.; Gris-Sánchez, I.; Knight, J.C.; de Sterke, C.M.; Eggleton, B.J. Highly-efficient, octave spanning soliton self-frequency shift using a specialized photonic crystal fiber with low OH loss. Opt. Express 2011, 19, 17766–17773.
Yuan, J.; Sang, X.; Yu, C.; Wang, K.; Yan, B.; Shen, X.; Han, Y.; Zhou, G.; Li, S.; Hou, L. Widely wavelength-tunable two-colored solitons and small spectral component for broadband mid-infrared wavelength generation in a highly birefringent photonic crystal fiber. IEEE Photonics Technol. Lett. 2012, 24, 670–672.
Szewczyk, O.; Pala, P.; Tarnowski, K.; Olszewski, J.; Vieira, F.S.; Lu, C.; Foltynowicz, A.; Mergo, P.; Sotor, J.; Soboń, G. Dual-wavelength pumped highly birefringent microstructured silica fiber for widely tunable soliton self-frequency shift. J. Light. Technol. 2021, 39, 3260–3268.
Bi, W.; Li, X.; Xing, Z.; Zhou, Q.; Fang, Y.; Gao, W.; Xiong, L.; Hu, L.; Liao, M. Wavelength conversion through soliton self-frequency shift in tellurite microstructured fiber with picosecond pump pulse. J. Appl. Phys. 2016, 119, 043102.
Alamgir, I.; Shamim, M.H.M.; Correr, W.; Messaddeq, Y.; Rochette, M. Mid-infrared soliton self-frequency shift in chalcogenide glass. Opt. Lett. 2021, 46, 5513–5516.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Optics

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ziwen Tang

Zihua Zheng

Boyao Li

Zhiyi Wei

Jinghua Sun

View Times: 175

Update Date: 20 Feb 2024

Table of Contents

Video Upload Options

Confirm