Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Hanan Almarashdi
 -- 2207 2024-01-25 19:04:35 |
2 format change
Peter Tang
 Meta information modification 2207 2024-01-26 06:39:18 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Almarashdi, H.S.; Mohamed, A.H.; Jarrah, A.M. Mathematics Enrichment Program. Encyclopedia. Available online: https://encyclopedia.pub/entry/54363 (accessed on 19 May 2024).
Almarashdi HS, Mohamed AH, Jarrah AM. Mathematics Enrichment Program. Encyclopedia. Available at: https://encyclopedia.pub/entry/54363. Accessed May 19, 2024.
Almarashdi, Hanan Shaher, Ahmed H. Mohamed, Adeeb M. Jarrah. "Mathematics Enrichment Program" Encyclopedia, https://encyclopedia.pub/entry/54363 (accessed May 19, 2024).
Almarashdi, H.S., Mohamed, A.H., & Jarrah, A.M. (2024, January 25). Mathematics Enrichment Program. In Encyclopedia. https://encyclopedia.pub/entry/54363
Almarashdi, Hanan Shaher, et al. "Mathematics Enrichment Program." Encyclopedia. Web. 25 January, 2024.
Mathematics Enrichment Program
Edit
This entry is adapted from the peer-reviewed paper 10.3390/su15054658

The mathematics enrichment activities aim to provide students with a stimulating mathematical experience, promote positive attitudes, raise the level of achievement, and contribute to efforts to enhance, generalize, and increase the general understanding of mathematics.

Mathematics Enrichment Program high-ability learners problem solving

1. Introduction

The focus of educational policy has recently begun to shift from completing compulsory education to ensuring quality education that will develop students to be ready for international competition. Likewise, one of the main pillars of the United Arab Emirates (UAE) National Agenda is to improve students’ competencies and abilities in diverse literacy skills in reading, mathematics, and science by developing an ideal and high-quality educational foundation [1]. The Program for International Student Assessment (PISA) examines the students’ ability to use mathematics to think about their lives, make plans for their future, and think about important problems and issues in their lives. Recently, the PISA results revealed a challenge for the UAE. The UAE students ranked in the 50th position in mathematics out of 79 countries in PISA 2018 [2]. Although Emirati students in PISA 2018 were leading the Arab countries as they scored the highest average performance in mathematics literacy compared to students of other Arab countries, the results indicated poor performance in general. PISA measures proficiency on a scale of one to six, with level 1 being the lowest. Only approximately 5% of UAE students can perform at the fifth and sixth levels, and nearly half of the students in the UAE still achieve below Level 2 [3].
One of the factors that cause PISA scores to drop is that students are not trained to solve contextual problems [4]. Most students have experienced “doing mathematics” which involves studying materials and working through abstract tasks. In contrast, PISA problems can be considered as one of the measures that address current social needs, focusing on students’ ability to solve real-life problems faced in modern society [5]. PISA problems are contextual in nature and are presented as word problems. Based on the literature, some reasons have been suggested to answer the question of why students are not very successful in solving word problems: first, students have limited experience with word problems [6]; second, lack of motivation to solve word problems [7]; and third, word problems were irrelevant to students’ lives [8]. This suggests that it is imperative to provide students with opportunities to become real-life problem solvers by exposing them to the type of problem that develops their problem-solving abilities [5].
Although remedial actions must be taken to help all students improve their learning levels, high-achieving students receive little attention despite their critical role in developing and transforming societies [9]. Long ago, in 1980, An Agenda for Action: Recommendations for School Mathematics stated that “outstanding mathematical ability is a precious societal resource, sorely needed to maintain leadership in a technological world” [10]. However, the discourse on equity focused primarily on providing access to a minimum of basic mathematics but ignored the high potential among disadvantaged students [11]. According to the Diversity in Mathematics Education Center for Learning and Teaching (DIME) [12], many countries report equity and learning opportunities primarily for low-achieving students and their chances of having some access to basic mathematics. Only recently, research and development have focused on the potential among underprivileged students, those who are not immediately identified as having high potential [11][13]. The “mathematical potential” construct is used for students “who can achieve a high level of mathematical performance when their potential is realized to the greatest extent” [14]. There is a call for a wider conceptualization of mathematical potential due to the economic demands raised by the huge need for STEM academics in a technical civilization. This concept of “mathematical potential” can be carried over from the top 2% to a wider group of about 20% of all students, and thus they are less exclusive than the usual “talented” or “gifted” [11].
The findings of a recent study by [15], which used the PISA framework to evaluate pupils’ mathematical literacy, were in line with those of the OECD [3]. The results revealed that students are comfortable addressing mathematical literacy problems at the low levels of 1–3 but struggle with problem-solving that requires higher-order thinking and reasoning problems at levels 4–6 where they scored only a 9% accuracy rate for level 4 questions, 5% for level 5, and only 2% for level 6. This suggests that there is a genuine need for intervention to raise these levels, particularly the performance of gifted and high achievers who can function at levels 5 and 6.

2. What Is Enrichment?

The Cambridge Dictionary [16] defines “enrichment” as “the act or process of improving the quality or power of something by adding something else” (para. 1). Enrichment is defined as any type of activity or learning that falls outside the core of the learning that most children do. The goal of enrichment is related to improving the quality of life in the classroom and increasing sensitivity [17]. The authors of [11] stated that enrichment means exposing the students to rich learning processes to expand their experiences and skills. However, enrichment is considered a relative concept as all definitions refer to normal practices that are not standardized in schools and classes [18]. Nevertheless, the enrichment curriculum will provide students with the opportunity to experience “the joy of confronting a novel situation and trying to make sense of it—the joy of banging your head against a mathematical wall, and then discovering that there may be ways of either going around or over that wall” [19].
Feng [18] points out that enrichment is a way to introduce accessible aspects of mathematics not covered by the curriculum, promote mathematical reasoning, encourage extended problem-solving, provide alternative approaches to curricular topics, and highlight links between aspects of mathematics presented separately in the curriculum. Thus, enrichment should not only be available to the fastest and brightest students but it should also be integrated into the curriculum. Moreover, enrichment is not only seen as a means for more capable students, but all students will also benefit from it; at least it can offer most students a more realistic option for classroom management [20].
The “enrichment of content” was defined as “any learning experience that replaces, supplements, or extends instruction beyond the restrictive bonds and boundaries of course content, textbook, and classroom and that includes depth of understanding, breadth of understanding, and relevance to the student and to the world in which he or she lives” [21]. In the same vein, ref. [20] focuses on depth, breadth, and relevance as major components of enrichment. To this end, there are two types of enrichment: obtained either through broadening or deepening. Enrichment through broadening represents learning additional topics rather than what is normally studied at school, while enrichment through deepening enhances the depth and complexity of the subject being studied in the school [11].
For the mathematics education field, enrichment is defined as “broadening students’ mathematical experiences by examining mathematics outside of the prescribed curriculum and also making connections with other curriculum areas” [22]. Additionally, enrichment in mathematics means allowing the learner to learn mathematics in more depth to expand the learner’s knowledge [23]. Enrichment through deepening the tasks and topics is mostly selected because it is in line with the regular curriculum unlike broadening through extracurricular activities [24]. For this research, the definition of enrichment as deepening and expanding students’ knowledge is chosen because it suits the needs of high-achieving students in regular classrooms through an emphasis on problem-solving and mathematical reasoning [20].

3. Paradigmatic Positions of Mathematics Enrichment

The enrichment activities aim to provide students with a stimulating mathematical experience, promote positive attitudes, raise the level of achievement, and contribute to efforts to enhance, generalize, and increase the general understanding of mathematics. From the enrichment literature, four paradigmatic positions can be identified to reflect educational views and priorities; Feng [18] listed enrichment positions as follows:
  • Development of exceptional mathematical talent (e.g., [25]);
  • Popular contextualization of mathematics (e.g., [26]);
  • Enhancement of mathematics learning processes (e.g., [20]); and
  • Outreach to the mathematically underprivileged (e.g., [27]).
According to Feng [18], the first position is directed to few students, only the gifted, as it aims to identify and develop mathematical talent. The second position applies to all students where the focus is on the application of mathematics as a means of engaging students in mathematics. This will make students appreciate the applications of mathematics in life, and not just as an academic discipline. This is expected to break the negative stereotypes of mathematics by deepening students’ understanding of mathematics and its applications [18]. The third position of enrichment is an approach to the ongoing process that should infuse all aspects of teaching and learning as an integral part of education for all students, whether in regular classrooms or beyond that is best described as student- and experience-centered [18]. The fourth position calls for social justice and equity; educators who support this view not only believe that enrichment should be open to all students, but also make proactive efforts to ensure mathematics enrichment for students who have not traditionally benefited from such provisions [18]. All of these mathematics enrichment positions are motivated to provide high-quality mathematics learning experiences. However, opposing views arose from differing perceptions of how to best achieve this and to whom it should be applied to achieve the most benefit.
The focus of this research is mainly on the third position to enhance the mathematics learning process while using contextual mathematics which will also lead to the satisfaction of the second position of enrichment as popular contextualization of mathematics. According to Feng [18], “using this interpretation of enrichment, the engagement of all students in meaningful mathematical practices is an essential and worthwhile part of education; this also forms the main goal of mathematics enrichment”. Enrichment tasks are often designed to use mathematical concepts and techniques at various levels of difficulty and may lead to qualitatively different endpoints [18][20]. If mathematics enrichment includes “mathematical problem solving and mathematical logic linked to mathematical contexts” [20], enrichment should be the basis for many, if not all, aspects of the curriculum, and all students should be able to benefit from this experience [18].

4. Mathematical Enrichment Content Framework

In this research, enrichment by deepening was adopted based on problem-solving and mathematical reasoning [20]. The problem-solving content entails the general scope of skills that can be applied both inside and outside of mathematics curricula [20]. Therefore, real-life applications can be incorporated into problem-solving to engage students in mathematics. Mathematical thinking is associated with specific mathematical skills that need to be drawn on for effective problem-solving. This enrichment program integrates PISA contextualized problems into its content that require thinking at a higher level, such as mathematical thinking [28]. Looking at the PISA 2021/2022 framework, the mathematics content is referred to as mathematical literacy that also covers problem-solving and reasoning [29][30]. Moreover, the components of mathematical literacy include mathematical thinking, such as reasoning and modeling [31]. These elements then work together and interact with both teachers and students as shown in Figure 1 [20].
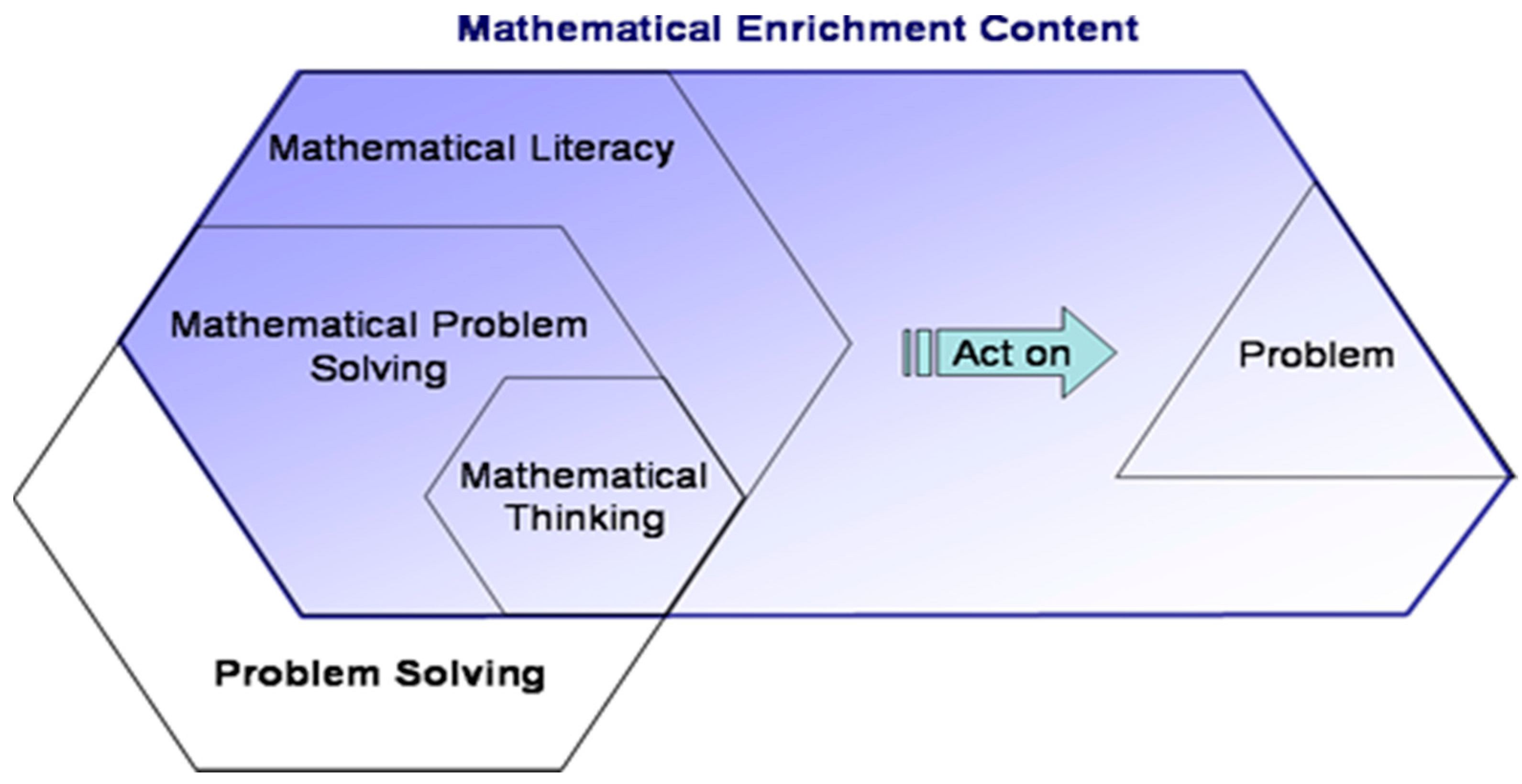
Figure 1. Mathematical Enrichment Content Framework.
PISA 2021/2022 [29][30] and Piggott [20] agree that learning general problem-solving skills will not suffice when teaching about problem-solving. Students also need mathematical thinking skills, because without them they would not have the skills to apply them to the problem-solving process. The reasoning is central to problem-solving (modeling processes) based on PISA 2021/2022 framework.
PISA aims to measure the students’ mathematical literacy that focuses on real-world problems as the students encounter situations and problems that go beyond what was learned in the school’s classroom [32]. Students are required to use the skills and competencies they acquired through their school learning to solve these contextual problems [32]. However, school mathematics curricula are usually structured into topics that focus on procedures and formulas. Mathematics is presented to students as a set of disjointed pieces of factual knowledge, not as overarching concepts and relationships [32]. Because of this organization, students may not be able to see or experience existing mathematics in new fields and applications [33].
For this content to make sense, learning and teaching environments need to encourage the effective use of resources so that students can develop the skills, strategies, and competence needed to effectively address problems and use basic thinking skills [20]. A specific view of teaching and learning supports engaging problems that develop and use problem-solving strategies and encourages mathematical thinking. Thus, teachers can apply Contextual Teaching and Learning (CTL) which is a method that helps the teachers relate subject content to real-world applications and motivate students to make connections [34][35]. There are several connections between the CTL steps and components of learning with indicators of mathematical literacy abilities [36]. Hence, mathematical literacy could be improved through the application of contextual learning.
This CTL approach reflects the constructive perspectives of learning through social interaction [37]. Constructivism emphasized, as a learning theory, the role of students rather than that of the teacher. In constructivism, students can use their prior knowledge and experience in testing ideas and apply these ideas to a new situation [34]. Learning aims to provide learners with learning situations to assimilate new learning together with prior knowledge to construct their unique cognition [38]. However, Swan [39] stressed the crucial role of students’ collaboration, building on the knowledge that students previously studied, and creating tension and cognitive conflict to be resolved by drawing on collective knowledge and discussion for multiple solution pathways. Non-routine problems let the students think of more than one solution and use more than one strategy. While the students work together and use their prior experience to gain new information in the process of problem-solving, the teacher’s role is to facilitate this collaboration.

References

  1. The Official Portal of the UAE Government. National Agenda. Available online: https://u.ae/en/about-the-uae/strategies-initiatives-and-awards/strategies-plans-and-visions/strategies-plans-and-visions-untill-2021/national-agenda (accessed on 7 February 2023).
  2. Sanderson, D. UAE Schools Improve in Maths But Lag Behind in Reading and Science, International Rankings Show. The National News. 3 December 2019. Available online: https://www.thenationalnews.com/uae/education/uae-schools-improve-in-maths-but-lag-behind-in-reading-and-science-international-rankings-show-1.946165 (accessed on 26 January 2023).
  3. OECD. United Arab Emirates: Country Note—PISA 2018 Results. Available online: https://www.oecd.org/pisa/publications/PISA2018_CN_ARE.pdf (accessed on 15 March 2020).
  4. Novita, R.; Putra, M. Using Task Like PISA’s Problem to Support Student’s Creativity in Mathematics. J. Math. Educ. 2016, 7, 31–42.
  5. Hong, J.Y.; Kim, M.K. Mathematical Abstraction in the Solving of Ill-Structured Problems by Elementary School Students in Korea. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 267–281.
  6. Bailey, T. Taking the Problems Out of Word Problems. Teach. PreK–8 2002, 32, 60–61.
  7. Hart, J.M. The Effect of Personalized Word Problems. Teach. Child. Math. 1996, 2, 504–505.
  8. Ensign, J. Linking Life Experiences to Classroom Math. In Proceedings of the Annual Meeting of the American Educational Research Association, Chicago, IL, USA, 24–28 March 1997.
  9. Meisenberg, G.; Lynn, R. Intelligence: A Measure of Human Capital in Nations. J. Soc. Political Econ. Stud. 2011, 36, 421–454.
  10. National Council of Teachers of Mathematics. An Agenda for Action; National Council of Teachers of Mathematics: Reston, VA, USA, 1980.
  11. Schnell, S.; Prediger, S. Mathematics Enrichment for All—Noticing and Enhancing Mathematical Potentials of Underprivileged Students as an Issue of Equity. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 143–165.
  12. Diversity in Mathematics Education Center for Learning and Teaching. Culture, Race, Power in Mathematics Education. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 405–433.
  13. Suh, J.; Fulginiti, K. Developing Mathematical Potential in Underrepresented Populations through Problem Solving, Mathematical Discourse and Algebraic Reasoning. In The Elements of Creativity and Giftedness in Mathematics; Sriraman, B., Lee, K., Eds.; Sense Publishing Inc.: Rotterdam, The Netherlands, 2011; Volume 1, pp. 67–79.
  14. Leikin, R. Bridging Research and Theory in Mathematics Education with Research and Theory in Creativity and Giftedness. In Creativity in Mathematics and the Education of Gifted Students; Leikin, R., Berman, A., Koichu, B., Eds.; Sense: Rotterdam, The Netherlands, 2009; pp. 383–409.
  15. Almarashdi, H.S.; Jarrah, A.M. Assessing Tenth-Grade Students’ Mathematical Literacy Skills in Solving PISA Problems. Soc. Sci. 2023, 12, 33.
  16. Cambridge University Press. Available online: https://dictionary.cambridge.org/dictionary/english/enrichment (accessed on 5 February 2023).
  17. Eyre, D.; Marjoram, T. Enriching and Extending the National Curriculum; Kogan Page Ltd.: London, UK, 1990.
  18. Feng, W. Conceptions of Mathematics Enrichment. In Proceedings of the British Educational Research Association (BERA) Annual Conference, Coventry, UK, 6–9 September 2006.
  19. Schoenfeld, A.H. Reflections on Doing and Teaching Mathematics. In Mathematical Thinking and Problem Solving; Schoenfeld, A.H., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1994; Volume 53–70.
  20. Piggott, J. Mathematics Enrichment: What is it and Who is it for? In Proceedings of the Annual Conference of the British Educational Research Association, University of Manchester, Manchester, UK, 15–18 September 2004.
  21. Clendening, C.P.; Davies, R.A. Challenging the Gifted: Curriculum Enrichment and Acceleration Models; R. R. Bowker Company: New York, NY, USA, 1983.
  22. Bicknell, B.A. Multiple Perspectives on the Education of Mathematically Gifted and Talented Students; Massey University: Palmerston North, New Zealand, 2009.
  23. Koshy, V. Teaching Gifted Children 4–7: A Guide for Teachers; David Fulton Publishers: London, UK, 2002.
  24. Sheffield, L.J. Extending the Challenge in Mathematics: Developing Mathematical Promise in K-8 Students; Corwin Press: Thousand Oaks, CA, USA, 2003.
  25. Roberts, J.L. Enrichment Opportunities for Gifted Learners; Prufrock Press Inc.: Austin, TX, USA, 2005.
  26. Zeeman, C. Christmas Lectures and Mathematics Master-Classes. In The Popularization of Mathematics; Howson, A.G., Kahane, J.-P., Eds.; Cambridge University Press: Cambridge, UK, 1990.
  27. Bouie, A. After School Success: Academic Enrichment Strategies with Urban Youth; Teachers College Press: New York, NY, USA, 2007.
  28. Ambarita, S.M.; Asri, L.; Agustina, A.; Octavianty, D.; Zulkardi. Mathematical Modeling Skills on Solving PISA Problems. J. Phys. Conf. Ser. 2018, 1097, 012115.
  29. OECD. Governing Board: PISA 2021 Mathematics Framework (First Draft). Available online: https://www.upc.smm.lt/naujienos/smm/penkiolikmeciu-matematinis-rastingumas/GB-2018-4-PISA-2021-Mathematics-Framework-First-Draft.pdf (accessed on 12 April 2019).
  30. OECD. PISA 2021 Mathematics Framework (Draft). Available online: http://www.oecd.org/pisa/pisaproducts/pisa-2021-mathematics-framework-draft.pdf (accessed on 1 May 2019).
  31. Stacey, K. What is Mathematical Thinking and Why is it Important? In Proceedings of the APEC-Tsukuba International Conference 2007: Innovative Teaching Mathematics through Lesson Study, Tokyo & Sapporo, Japan, 2–7 December 2006; pp. 4–13.
  32. OECD. PISA 2009 Assessment Framework Key Competencies in Reading, Mathematics and Science; OECD: Paris, France, 2009.
  33. Brown, J.S.; Collins, A.; Duguid, P. Situated Cognition and the Culture of Learning. Educ. Res. 1989, 18, 32–42.
  34. Berns, R.G.; Erickson, P.M. Contextual Teaching and Learning: Preparing Students for the New Economy. Highlighted Zone Res. @Work. 2001, 2, 1–8.
  35. Hudson, C.; Whisler, V.R. Contextual Teaching and Learning for Practitioners. J. Syst. Cybern. Inform. 2008, 6, 54–58.
  36. Maryani, N.; Widjajanti, D.B. Mathematical Literacy: How to Improve it Using Contextual Teaching and Learning Method? J. Phys. Conf. Ser. 2020, 1581, 012044.
  37. Confrey, J. What Constructivism Implies for Teaching. J. Res. Math. Educ. 1990, 4, 107–210.
  38. Ertmer, P.A.; Newby, T.J. Behaviorism, Cognitivism, Constructivism: Comparing Critical Features from an Instructional Design Perspective. Perform. Improv. Q. 2013, 26, 43–71.
  39. Swan, M. Designing a Multiple Representation Learning Experience in Secondary Algebra. Educ. Des. 2008, 1, 1–17.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Education & Educational Research
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Hanan Shaher Almarashdi
,
Ahmed H. Mohamed
,
Adeeb M. Jarrah
View Times: 172
Revisions: 2 times (View History)
Update Date: 26 Jan 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback