To Solve Scheduling Problems to Minimize Carbon Footprint

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Marichelvam Mariappan Kadarkarainadar	--	2532	2024-01-13 08:02:38	\|
2	layout	Camila Xu	Meta information modification	2532	2024-01-15 02:21:35	\|

This entry is adapted from the peer-reviewed paper 10.3390/pr12010143

Effective scheduling is an important method proposed by some shop floor engineers and operational analysts to minimize carbon emissions. Scheduling always has a key role in the manufacturing environment and operations management. There is a direct link between the energy consumption of a manufacturing facility and its environmental impact, which is mostly analyzed as a carbon footprint.

carbon footprint hybrid flow shop scheduling pigeon-inspired optimization algorithm (PIOA)

1. Introduction

The main objective of any manufacturing or service industry is to make a profit. The latest technological developments and the concepts of industrial engineering help these industries maximize their profits. But, in recent times, managers seem to understand that profit is not the only real goal to achieve. Leaving a positive impact on future generations in a sustainable environment also turns out to be important ^[1]. Ongoing usage of resources without thinking about their environmental effects becomes the main problem in most manufacturing companies. Thus, today the scenario has changed due to the universal environmental rules and regulations. Although there are different strategies to lessen the impacts on our world, better utilization of resources or reducing the waste of production facilities become the main research topics of the literature ^[2]. One of the proper ways to achieve these goals should be by designing a better schedule in a workshop environment.

It is our collective responsibility to reduce carbon emissions to mitigate the effects of greenhouse gas emissions, global warming, and climate change. Environment-friendly production also has a positive impact on consumers, which also increases their loyalty to the related companies. Therefore, most industries in the world attempt to lessen carbon emissions by adopting different strategies. In recent years, several researchers have attempted to reduce carbon emissions with the help of their potential research activities. Effective scheduling is an important method proposed by some shop floor engineers and operational analysts to minimize carbon emissions ^[3]^[4]. Scheduling always has a key role in the manufacturing environment and operations management. Overall, scheduling can be identified as the process of distributing existing inadequate resources in an effective manner to maximize or minimize certain objective functions ^[5]. Many scheduling environments are described in the literature, including flexible manufacturing system (FMS) scheduling, job shop scheduling, hybrid flow shop (HFS) scheduling, flow shop scheduling, parallel machine scheduling, single machine scheduling, and flexible job shop scheduling ^[6]. Among them, HFS scheduling is an important research area as many industries, such as textiles ^[7], furniture manufacturing ^[8], automobile component manufacturing ^[9], chemical industries ^[10], electronics industries ^[11], etc., resemble the HFS environment. The general layout of an HFS environment can be seen in Figure 1 ^[8].

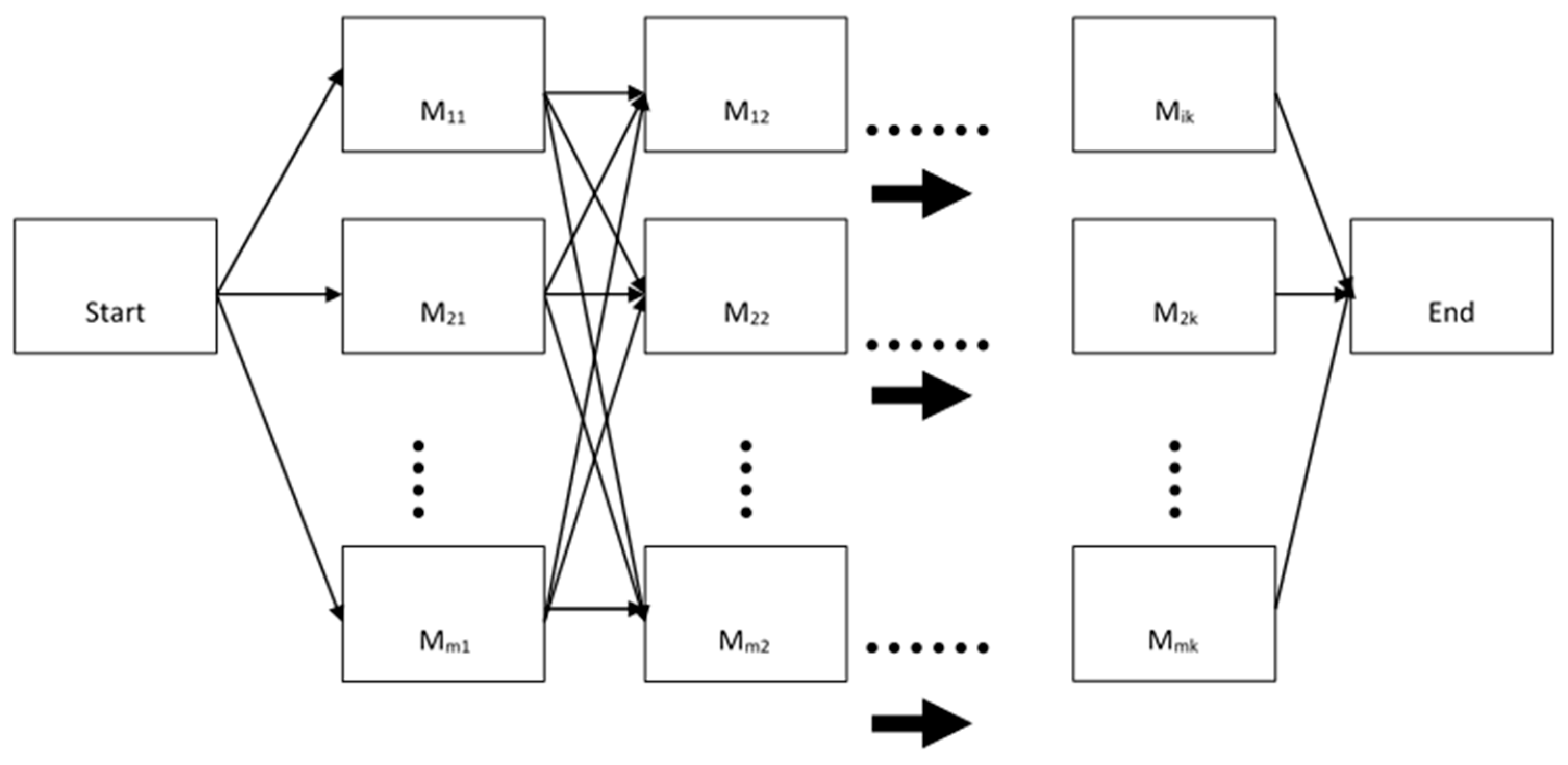
Figure 1. Layout of an HFS environment.

Arthanari and Ramamurthy ^[12] have addressed the HFS scheduling problems in their research. According to the research, the HFS scheduling problem is a type of combinatorial optimization problem that is NP-hard, or non-deterministic polynomial-time hard ^[13]^[14]. Therefore, exact solution techniques for these problems are difficult to obtain when the problem size ranges from moderate to large. Therefore, researchers use different types of heuristics and metaheuristics to solve HFS scheduling problems. Nowadays, scheduling researchers also concentrate on the reduction of carbon emissions. There is a discrepancy between the theoretical analysis and the actual requirements of industries, even though numerous scheduling researchers have addressed various scheduling problems with various goal functions ^[15]^[16].

2. Scheduling Problems with Carbon Footprint Minimization Objective

There is a direct link between the energy consumption of a manufacturing facility and its environmental impact, which is mostly analyzed as a carbon footprint. Mouzon & Yildirim ^[17] developed a novel greedy randomized adaptive metaheuristic algorithm for multiple objectives to minimize the total energy consumption and total delay in a single machine environment. By minimizing energy consumption, they reduced their carbon footprint. Fang et al. ^[18] developed a novel mathematical approach to minimize the peak energy load, power consumption, and associated carbon footprint in a cast iron plate manufacturing plant. An enhanced genetic simulated annealing algorithm (GSAA) was used to reduce the makespan and energy consumption in a flexible flow shop environment ^[19]. A multiobjective ant colony optimization algorithm (MOACO) was presented by Luo et al. ^[20] for minimizing the makespan and electricity usage. A multi-objective genetic algorithm (MOGA) was investigated by Liu and Huang ^[21] to decrease the carbon footprint by minimizing the total weighted tardiness. In another multi-objective study, a teaching and learning-based optimization algorithm (MTLBOA) was proposed by Lin et al. ^[22] for finding the best process constraints in turning industry with makespan and also the carbon footprint.

Ding et al. ^[23] studied a hybrid model of the NEH heuristic and an iterated greedy algorithm to analyze the flow shop scheduling environment with numerous objectives. They developed a multiobjective solution strategy with makespan minimization and total carbon emission minimization in their work. They generated several random problem instances with numerous numbers of jobs and machines to validate the given methods. The computational solutions were measured against several algorithms given in the literature and proved to be better. Yan et al. ^[24] developed a multi-level optimization solution approach to obtain better results for the energy-efficient flexible flow shop scheduling environment under the makespan and total energy usage. After developing a mathematical model, the genetic algorithm (GA) was used to find the optimal schedules. The effectiveness of the given method was investigated using a case study. Lei et al. ^[25] introduced a teaching-learning-based optimization algorithm (TLBOA) for finding the minimum of the total energy usage and total tardiness in an HFS problem. The HFS scheduling problem was divided into three sub-problems, and a three-string coding method was used for the solution representation of these sub-problems. Several test instances were solved to analyze the efficiency of the given approach. Liu et al. ^[26] investigated the efficiency of a fruit fly optimization algorithm (FFOA) for minimizing the carbon footprints of all products and makespan in a flexible job shop environment using the data from a case problem. They identified product carbon footprints using the relationships between resources and products using these resources.

In their study, Zhang et al. ^[27] integrated the minimum values of total electricity usage and carbon footprint into the objective function of their algorithm. Additionally, they incorporated the utilization of total energy and carbon emissions as constraints in their proposed approach. The researchers put forth the use of integer programming as a means to solve the mathematical model. Lu et al. ^[28] designed a multi-objective approach for the multi-stage HFS problems under makespan, noise pollution, and overall energy consumption. An improved gray-wolf algorithm was used to solve the problems. Nasiri et al. ^[29] used an integer programming method to reduce the sum of weighted tardiness and energy usage in an HFS environment. Pan et al. ^[30] developed an effective imperialist competitive algorithm (ICA) for multiobjective, low-carbon parallel machine scheduling. Piroozfard et al. ^[31] analyzed the minimization of the sum of the carbon footprint and total late work indicators in a flexible job shop environment. To achieve this objective, they employed a MOGA. The authors indicated that the choice of these two roles was indicative of aspirations rooted in sustainability and classical principles.

Wu et al. ^[32] analyzed a multi-criterion, flexible flow shop scheduling environment considering makespan and low-carbon scheduling objectives. The carbon emissions were measured with the use of renewable and non-renewable energy on a machine. They proposed a GA-based solution in their work. Meng et al. ^[33] analyzed the HFS problem to minimize the overall energy consumption under makespan and energy usage that can be varied under machines with different turning on/off state constraints. GA was used for solving the integrated mathematical model. Zhou and Liu ^[34] analyzed the effect of environmental pollution and increasing energy costs within an HFS with fuzzy processing times. Total weighted delivery time and energy usage were the objective functions. Chen et al. ^[35] have attempted to decrease the energy expenditure and minimize the completion time of a production system. They developed a multi-objective mixed-integer modeling approach to achieve energy efficiency HFS with lot streaming for the minimizing of the sum of two objectives, which are the makespan of the production and electric power usage.

Wang et al. ^[36] investigated a real-life scenario of a glass manufacturing business. A two-stage HFS in which machine eligibility in the first phase and batch machine in the following phase were selected. Similar to previous studies, makespan and total energy usage (which is preferred to reflect energy-efficient manufacturing) were used to measure the process. They considered time-of-use electricity prices and machine states (given as online, off, and idle) in their research. Different local search-based metaheuristics were used. The study conducted by Cai and Lei ^[37] addressed the management of a distributed energy-efficient hybrid flow shop scheduling environment that incorporates fuzzy processing time. To optimize the scheduling process, they introduced a cooperative shuffled frog-leaping algorithm (CSFLA). The objective of the research was to simultaneously determine the optimal values for fuzzy makespan, total agreement index, and fuzzy total energy usage. Shi et al. ^[38] studied a sustainable HFS environment under consideration of processing time, energy consumption, and carbon emissions. Using GA, dynamic scheduling was analyzed. Wang and Wang ^[39] investigated the energy-focused distributed HFS, considering makespan and energy usage. Using a multi-objective approach, a hybridized cooperative memetic algorithm (HCMA) was proposed to obtain optimal solutions. Zuo et al. ^[40] addressed the energy-efficient HFS scheduling problems considering the objectives of makespan, total tardiness, and total energy usage. With these objectives, the green scheduling and sustainable manufacturing needs of policymakers were achieved. Under variable speed constraints, an artificial bee colony algorithm (ABCA)-based solution methodology was developed.

3. Pigeon-Inspired Optimization Algorithm (PIOA)

The pigeon-inspired optimization algorithm (PIOA) is a metaheuristic based on swarm intelligence that was developed by Duan and Qiao ^[41]. The algorithm imitates the natural action pattern of pigeons in nature. While moving within a swarm, each member of this swarm (pigeons) has their own position, velocity, and personal best position; both of these are used for understanding their moves in a search space. The search activity of pigeons can be analyzed in two different phases: the first is based on their movements, while the second is related to the other pigeons in the swarm. The simple PIOA is described in ^[42]^[43]^[44].

Goel ^[45] used PIOA to search for the shortest path from a given point and measured the efficiency of the approach using Dijkstra’s algorithm. Hao et al. ^[46] enhanced the basic PIOA to solve the unmanned aerial vehicle (UAV) assignment problem under energy consumption. Sun and Duan ^[47] modified the PIOA with the prey–predator strategy to prevent the algorithm from trapping into a locally optimal solution. Their proposed approach was used for protein–protein interaction (PIP) parameter adjustment. Zhang and Duan ^[48] suggested a predator–prey pigeon-inspired optimization (PPPIO) algorithm to solve the three-dimensional path planning problem of UAVs. The authors put forth the concept of predator–prey dynamics as a means to improve the overall characteristics of global optimization and accelerate the convergence rate. The researchers demonstrated that the performance of the PPPIO technique outperformed both the PIOA and particle swarm optimization (PSO) algorithms. Deng et al. ^[49] integrated the PIOA with membrane computing to address the parameter design challenges encountered in an industrial motor.

According to the findings of Hu et al. ^[50], the utilization of PIOA in certain intricate settings results in the attainment of local optima, a sluggish rate of convergence, and unstable solution attributes. Therefore, to deal with these shortcomings, they applied an adaptive weighted approach to PIOA and analyzed the UAV route planning problem. Pei et al. ^[51] combined PIOA with the quantum chaotic process to find the optimal fuzzy control strategy for a hybrid electric vehicle. Rehman et al. ^[52] hybridized the PIOA with the GA to minimize electricity costs while minimizing user discomfort. Liu et al. ^[53] developed an improved PIOA to cope with a nonlinear optimization problem. In the improved IPIOA, the authors introduced PSO, an inverse factor, and a Gaussian factor, and better results were obtained. Shang et al. ^[54] addressed a multi-objective PIO (MOPIO) approach to solve a community detection problem in network science with negative ratio associations and ratio cuts. They proposed a crossover strategy to enhance the solution quality. They compared the quality of results from their algorithm with other multi-objective algorithms studied in previous papers from the literature and concluded that the MOPIO solution methodology provided better results. Modified and improved versions of binary PIOA were studied by the researchers to solve optimization problems in different fields ^[55]^[56]. The researchers have created enhanced iterations of PIOA to address the challenges posed by the dynamic facility layout problem ^[57] and the 0–1 knapsack problem ^[58]. An oppositional PIOA was suggested in ^[59] to solve the economic load dispatching problems. There are only a few studies in which PIOA is applied to scheduling problems. Fu et al. ^[60] studied a fuzzy production environment under maintenance. The MOPIO algorithm was developed using fuzzy makespan as the secondary objective. Wu et al. ^[61] applied PIOA to address the flexible job shop scheduling problem (FJSP) to minimize the makespan. Lei et al. ^[62] proposed a hybrid bat and pigeon for solving autonomous vehicle navigation and mapping. Ding and Dong ^[63] developed an improved PIOA to solve the continuous function optimization problem. Recently, Torky et al. ^[64] solved the financial crisis problems using the PIOA.

4. Firefly Algorithm (FA)

The recent versions of FA and their applications were addressed in ^[65]. The study conducted by Marichelvam et al. ^[66] examined the HFS scheduling environment, specifically focusing on analyzing the makespan and mean flow time using the FA. Karthikeyan et al. ^[67] proposed a solution methodology for addressing the challenges posed by multi-objective flexible job shop scheduling problems. The integration of local search techniques with FA effectively manages the maximum completion time, workload of the crucial machine, and total workload. In Fan et al. ^[68], a two-stage HFS environment with part arrivals and on-time delivery rate criteria was solved with FA. Marichelvam and Geetha ^[69] used FA to minimize the weighted sum of makespan, total flow time, and machine idle time in a multi-stage environment. Chakaravarthy et al. ^[70] analyzed the performance of the FA against the AIS (artificial immune system) algorithm for makespan and total flow time criteria in the m-machine flow shop scheduling problem. It is a given that both algorithms give better solution quality than other well-known solution methodologies.

Marichelvam and Geetha ^[71] investigated total flow time minimization for the m-machine flow shop scheduling problems. Qamhan et al. ^[72] integrated periodic maintenance, setup times, and release dates with makespan in a real-life problem. A hybridized FA was used for the solution. A chaos-based FA was proposed by Lo et al. ^[73] to solve the permutation flow shop scheduling problems under makespan. Kaya et al. ^[74] improved the efficiency of FA with chaos theory and local search strategies for makespan in a flow shop scheduling environment. Rashid and Osman ^[75] studied the energy-efficient HFS under makespan and energy utilization. Comparing FA against other well-known metaheuristics shows the superiority of the developed FA in the problem. The details of the FA to solve various applications can be seen in ^[76]^[77]. Ghasemi et al. ^[78] developed a new version of FA with improved global exploration for optimization problems in engineering. Bacanin et al. ^[79] solved the feature selection problem using the FA. Ezzeldin et al. ^[80] hybridized FA with GA and a particle swarm optimization algorithm to solve water distribution network problems. Sheeba and Uma Maheswari ^[81] proposed an enhanced FA for cloud computing applications. Recently, Villaruz et al. ^[82] suggested a scouting FA to solve global optimization problems.

References

Assia, S.; El Abbassi, I.; El Barkany, A.; Darcherif, M.; El Biyaali, A. Green scheduling of jobs and flexible periods of maintenance in a two-machine flowshop to minimize makespan, a measure of service level and total energy consumption. Adv. Oper. Res. 2020, 2020, 9732563.
Alvarez-Meaza, I.; Zarrabeitia-Bilbao, E.; Rio-Belver, R.M.; Garechana-Anacabe, G. Green scheduling to achieve green manufacturing: Pursuing a research agenda by mapping science. Technol. Soc. 2021, 67, 101758.
Hidri, L.; Alqahtani, A.; Gazdar, A.; Ben Youssef, B. Green scheduling of identical parallel machines with release date, delivery time and no-idle machine constraints. Sustainability 2021, 13, 9277.
Li, Y.Z.; Pan, Q.K.; Gao, K.Z.; Tasgetiren, M.F.; Zhang, B.; Li, J.Q. A green scheduling algorithm for the distributed flowshop problem. Appl. Soft Comput. 2021, 109, 107526.
Baker, K.R.; Trietsch, D. Principles of Sequencing and Scheduling, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 1–3.
Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems, 4th ed.; Springer: New York, NY, USA, 2012; pp. 13–33.
Grabowski, J.; Pempera, J. Sequencing of jobs in some production system. Eur. J. Oper. Res. 2000, 125, 535–550.
Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl. Soft Comput. 2014, 19, 93–101.
Marichelvam, M.K.; Geetha, M. Application of novel harmony search algorithm for solving hybrid flow shop scheduling problems to minimise makespan. Int. J. Ind. Syst. Eng. 2016, 23, 467–481.
Deal, D.E.; Yang, T.; Hallquist, S. Job scheduling in petrochemical production: Two-stage processing with finite intermediate storage. Comput. Chem. Eng. 1994, 18, 333–344.
Jin, Z.H.; Ohno, K.; Ito, T.; Elmaghraby, S.E. Scheduling hybrid flowshops in printed circuit board assembly lines. Prod. Oper. Manag. 2002, 11, 216–230.
Arthanari, T.S.; Ramamurthy, K.G. An extension of two machines sequencing problem. Oper. Res. 1971, 8, 10–22.
Gupta, J.N. Two-stage, hybrid flowshop scheduling problem. J. Oper. Res. Soc. 1988, 39, 359–364.
Hoogeveen, J.A.; Lenstra, J.K.; Veltman, B. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard. Eur. J. Oper. Res. 1996, 89, 172–175.
Ruiz, R.; Vázquez-Rodríguez, J.A. The hybrid flow shop scheduling problem. Eur. J. Oper. Res. 2010, 205, 1–18.
Tosun, Ö.; Marichelvam, M.K.; Tosun, N. A literature review on hybrid flow shop scheduling. Int. J. Adv. Oper. Manag. 2020, 12, 156–194.
Mouzon, G.; Yildirim, M.B. A framework to minimise total energy consumption and total tardiness on a single machine. Int. J. Sustain. Eng. 2008, 1, 105–116.
Fang, K.; Uhan, N.; Zhao, F.; Sutherland, J.W. A new approach to scheduling in manufacturing for power consumption and carbon footprint reduction. J. Manuf. Syst. 2011, 30, 234–240.
Dai, M.; Tang, D.; Giret, A.; Salido, M.A.; Li, W.D. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robot. Comput. Integ. Manuf. 2013, 29, 418–429.
Luo, H.; Du, B.; Huang, G.Q.; Chen, H.; Li, X. Hybrid flow shop scheduling considering machine electricity consumption cost. Int. J. Prod. Econ. 2013, 146, 423–439.
Liu, C.H.; Huang, D.H. Reduction of power consumption and carbon footprints by applying multi-objective optimisation via genetic algorithms. Int. J. Prod. Res. 2014, 52, 337–352.
Lin, W.; Yu, D.Y.; Zhang, C.; Liu, X.; Zhang, S.; Tian, Y.; Xie, Z. A multi-objective teaching−learning-based optimization algorithm to scheduling in turning processes for minimizing makespan and carbon footprint. J. Clean. Prod. 2015, 101, 337–347.
Ding, J.Y.; Song, S.; Wu, C. Carbon-efficient scheduling of flow shops by multi-objective optimization. Eur. J. Oper. Res. 2016, 248, 758–771.
Yan, J.; Li, L.; Zhao, F.; Zhang, F.; Zhao, Q. A multi-level optimization approach for energy-efficient flexible flow shop scheduling. J. Clean. Prod. 2016, 137, 1543–1552.
Lei, D.; Gao, L.; Zheng, Y. A novel teaching-learning-based optimization algorithm for energy-efficient scheduling in hybrid flow shop. IEEE Trans. Eng. Manag. 2017, 65, 330–340.
Liu, Q.; Zhan, M.; Chekem, F.O.; Shao, X.; Ying, B.; Sutherland, J.W. A hybrid fruit fly algorithm for solving flexible job-shop scheduling to reduce manufacturing carbon footprint. J. Clean. Prod. 2017, 168, 668–678.
Zhang, Y.; Liu, Q.; Zhou, Y.; Ying, B. Integrated optimization of cutting parameters and scheduling for reducing carbon emissions. J. Clean. Prod. 2017, 149, 886–895.
Lu, C.; Gao, L.; Li, X.; Zheng, J.; Gong, W. A multi-objective approach to welding shop scheduling for makespan, noise pollution and energy consumption. J. Clean. Prod. 2018, 196, 773–787.
Nasiri, M.M.; Abdollahi, M.; Rahbari, A.; Salmanzadeh, N.; Salesi, S. Minimizing the energy consumption and the total weighted tardiness for the flexible flowshop using NSGA-II and NRGA. J. Ind. Syst. Eng. 2018, 11, 150–162.
Pan, Z.; Lei, D.; Zhang, Q. A new imperialist competitive algorithm for multiobjective low carbon parallel machines scheduling. Math. Probl. Eng. 2018, 2018, 5914360.
Piroozfard, H.; Wong, K.Y.; Wong, W.P. Minimizing total carbon footprint and total late work criterion in flexible job shop scheduling by using an improved multi-objective genetic algorithm. Res. Conser. Recycl. 2018, 128, 267–283.
Wu, X.; Shen, X.; Cui, Q. Multi-objective flexible flow shop scheduling problem considering variable processing time due to renewable energy. Sustainability 2018, 10, 841.
Meng, L.; Zhang, C.; Shao, X.; Ren, Y.; Ren, C. Mathematical modelling and optimisation of energy-conscious hybrid flow shop scheduling problem with unrelated parallel machines. Int. J. Prod. Res. 2019, 57, 1119–1145.
Zhou, B.; Liu, W. Energy-efficient multi-objective scheduling algorithm for hybrid flow shop with fuzzy processing time. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 1282–1297.
Chen, T.L.; Cheng, C.Y.; Chou, Y.H. Multi-objective genetic algorithm for energy-efficient hybrid flow shop scheduling with lot streaming. Ann. Oper. Res. 2020, 290, 813–836.
Wang, S.; Wang, X.; Chu, F.; Yu, J. An energy-efficient two-stage hybrid flow shop scheduling problem in a glass production. Int. J. Prod. Res. 2020, 58, 2283–2314.
Cai, J.; Lei, D. A cooperated shuffled frog-leaping algorithm for distributed energy-efficient hybrid flow shop scheduling with fuzzy processing time. Complex Intell. Syst. 2021, 7, 2235–2253.
Shi, L.; Guo, G.; Song, X. Multi-agent based dynamic scheduling optimisation of the sustainable hybrid flow shop in a ubiquitous environment. Int. J. Prod. Res. 2021, 59, 576–597.
Wang, J.J.; Wang, L. A cooperative memetic algorithm with learning-based agent for energy-aware distributed hybrid flow-Shop scheduling. IEEE Trans. Evol. Comput. 2022, 26, 461–475.
Zuo, Y.; Fan, Z.; Zou, T.; Wang, P. A Novel Multi-Population Artificial Bee Colony Algorithm for Energy-Efficient Hybrid Flow Shop Scheduling Problem. Symmetry 2021, 13, 2421.
Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37.
Duan, H.; Wang, X. Echo state networks with orthogonal pigeon-inspired optimization for image restoration. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 2413–2425.
Varun, A.; Kumar, M.S. A comprehensive review of the pigeon-inspired optimization algorithm. Int. J. Eng. Technol. 2018, 7, 758–761.
Zhong, Y.; Wang, L.; Lin, M.; Zhang, H. Discrete pigeon-inspired optimization algorithm with Metropolis acceptance criterion for large-scale traveling salesman problem. Swarm Evolut. Comput. 2019, 48, 134–144.
Goel, S. Pigeon optimization algorithm: A novel approach for solving optimization problems. In Proceedings of the 2014 International Conference on Data Mining and Intelligent Computing, Delhi, India, 5–6 September 2014.
Hao, R.; Luo, D.; Duan, H. Multiple UAVs mission assignment based on modified pigeon-inspired optimization algorithm. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014.
Sun, H.; Duan, H. PID controller design based on prey-predator pigeon-inspired optimization algorithm. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014.
Zhang, B.; Duan, H. Predator-Prey Pigeon-Inspired Optimization for UAV Three-Dimensional Path Planning. In Advances in Swarm Intelligence, 1st ed.; Tan, Y., Shi, Y., Coello, C.A.C., Eds.; Springer: Cham, Switzerland, 2014; Volume 8795, pp. 96–105.
Deng, Y.; Zhu, W.; Duan, H. Hybrid membrane computing and pigeon-inspired optimization algorithm for brushless direct current motor parameter design. Sci. China Technol. Sci. 2016, 59, 1435–1441.
Hu, C.; Xia, Y.; Zhang, J. Adaptive operator quantum-behaved pigeon-inspired optimization algorithm with application to UAV path planning. Algorithms 2018, 12, 3.
Pei, J.; Su, Y.; Zhang, D. Fuzzy energy management strategy for parallel HEV based on pigeon-inspired optimization algorithm. Sci. China Technol. Sci. 2017, 60, 425–433.
Rehman, M.H.A.; Javaid, N.; Iqbal, M.N.; Abbas, Z.; Awais, M.; Khan, A.J.; Qasim, U. Demand side management using hybrid genetic algorithm and pigeon inspired optimization techniques. In Proceedings of the 2018 IEEE 32nd International Conference on Advanced Information Networking and Applications, Kraków, Poland, 16–18 May 2018.
Liu, H.; Yan, X.; Wu, Q. An improved pigeon-inspired optimisation algorithm and its application in parameter inversion. Symmetry 2019, 11, 1291.
Shang, J.; Li, Y.; Sun, Y.; Li, F.; Zhang, Y.; Liu, J.X. MOPIO: A Multi-Objective Pigeon-Inspired Optimization Algorithm for Community Detection. Symmetry 2020, 13, 49.
Bolaji, A.L.A.; Okwonu, F.Z.; Shola, P.B.; Balogun, B.S.; Adubisi, O.D. A modified binary pigeon-inspired algorithm for solving the multi-dimensional knapsack problem. J. Intell. Syst. 2021, 30, 90–103.
Pan, J.S.; Tian, A.Q.; Chu, S.C.; Li, J.B. Improved binary pigeon-inspired optimization and its application for feature selection. Appl. Intell. 2021, 51, 8661–8679.
Zhun, X.; Liyun, X.; Xufeng, L. An Improved Pigeon-inspired Optimization Algorithm for Solving Dynamic Facility Layout Problem with Uncertain Demand. Procedia CIRP 2021, 104, 1203–1208.
Hussein, R.B.; Algamal, Z. Solving 0–1 knapsack problem by an improved binary Pigeon Inspired Optimization Algorithm. Math. Stat. Eng. Appl. 2022, 71, 312–324.
Ramalingam, R.; Karunanidy, D.; Alshamrani, S.S.; Rashid, M.; Mathumohan, S.; Dumka, A. Oppositional Pigeon-Inspired Optimizer for Solving the Non-Convex Economic Load Dispatch Problem in Power Systems. Mathematics 2022, 10, 3315.
Fu, X.; Chan, F.T.; Niu, B.; Chung, N.S.; Qu, T. A multi-objective pigeon inspired optimization algorithm for fuzzy production scheduling problem considering mould maintenance. Sci. China Inform. Sci. 2019, 62, 1–18.
Wu, X.; Shen, X.; Zhao, N.; Wu, S. An improved discrete pigeon-inspired optimisation algorithm for flexible job shop scheduling problem. Int. J. Bio-Inspired Comput. 2020, 16, 181–194.
Lei, T.; Luo, C.; Sellers, T.; Rahimi, S. A bat-pigeon algorithm to crack detection-enabled autonomous vehicle navigation and mapping. Intell. Syst. Appl. 2021, 12, 20053.
Ding, G.; Dong, F. An improved pigeon-inspired optimisation for continuous function optimisation problems. Int. J. Comput. Sci. Math. 2023, 17, 207–219.
Torky, M.; Gad, I.; Hassanien, A.E. Explainable AI Model for Recognizing Financial Crisis Roots Based on Pigeon Optimization and Gradient Boosting Model. Int. J. Comput. Intell. Syst. 2023, 16, 50.
Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36–50.
Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. A discrete firefly algorithm for the multi-objective hybrid flowshop scheduling problems. IEEE Trans. Evol. Comput. 2013, 18, 301–305.
Karthikeyan, S.; Asokan, P.; Nickolas, S. A hybrid discrete firefly algorithm for multi-objective flexible job shop scheduling problem with limited resource constraints. Int. J. Adv. Manuf. Technol. 2014, 72, 1567–1579.
Fan, B.; Yang, W.; Zhang, Z. Solving the two-stage hybrid flow shop scheduling problem based on mutant firefly algorithm. J. Ambient Intell. Humaniz. Comput. 2019, 10, 979–990.
Marichelvam, M.K.; Geetha, M. Solving tri-objective multistage hybrid flow shop scheduling problems using a discrete firefly algorithm. Int. J. Intell. Eng. Inform. 2014, 2, 284–303.
Chakaravarthy, G.V.; Marimuthu, S.; Sait, A.N. Comparison of firefly algorithm and artificial immune system algorithm for lot streaming in m-machine flow shop scheduling. Int. J. Comput. Intell. Syst. 2012, 5, 1184–1199.
Marichelvam, M.K.; Geetha, M. A hybrid discrete firefly algorithm to solve flow shop scheduling problems to minimise total flow time. Int. J. Bio-Inspired Comput. 2016, 8, 318–325.
Qamhan, M.A.; Qamhan, A.A.; Al-Harkan, I.M.; Alotaibi, Y.A. Mathematical modeling and discrete firefly algorithm to optimize scheduling problem with release date, sequence-dependent setup time, and periodic maintenance. Math. Prob. Eng. 2019, 2019, 8028759.
Lo, H.L.; Fong, S.; Zhuang, Y.; Wang, X.; Hanne, T. Applying a chaos-based firefly algorithm to the permutation flow shop scheduling problem. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence, Bali, Indonesia, 7–8 December 2015.
Kaya, S.; Gümüşçü, A.; Aydilek, İ.B.; Karaçizmeli, İ.H.; Tenekeci, M.E. Solution for flow shop scheduling problems using chaotic hybrid firefly and particle swarm optimization algorithm with improved local search. Soft Comput. 2021, 25, 7143–7154.
Rashid, M.F.F.A.; Osman, M.A.H. Optimisation of energy efficient hybrid flowshop scheduling problem using firefly algorithm. In Proceedings of the 2020 IEEE 10th Symposium on Computer Applications & Industrial Electronics, Penang, Malaysia, 18–19 April 2020.
Tilahun, S.L.; Ngnotchouye, J.M.T.; Hamadneh, N.N. Continuous versions of firefly algorithm: A review. Artif. Intell. Rev. 2019, 51, 445–492.
Kumar, V.; Kumar, D. A systematic review on firefly algorithm: Past, present, and future. Arch. Comput. Methods Eng. 2021, 28, 3269–3291.
Ghasemi, M.; Kadkhoda Mohammadi, S.; Zare, M.; Mirjalili, S.; Gil, M.; Hemmati, R. A new firefly algorithm with improved global exploration and convergence with application to engineering optimization. Decis. Analyt. J. 2022, 5, 100125.
Bacanin, N.; Venkatachalam, K.; Bezdan, T.; Zivkovic, M.; Abouhawwash, M. A novel firefly algorithm approach for efficient feature selection with COVID-19 dataset. Microprocess. Microsyst. 2023, 98, 104778.
Ezzeldin, R.; Zelenakova, M.; Abd-Elhamid, H.F.; Pietrucha-Urbanik, K.; Elabd, S. Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks. Water 2023, 15, 1906.
Sheeba, A.; Uma Maheswari, B. An efficient fault tolerance scheme based enhanced firefly optimization for virtual machine placement in cloud computing. Concurr. Comput. Pract. Exp. 2023, 35, e7610.
Villaruz, J.A.; Gerardo, B.D.; Gamao, A.O.; Medina, R.P. Scouting Firefly Algorithm and its Performance on Global Optimization Problems. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 445–451.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Industrial

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

M. Geetha

R. Chandra Guru Sekar

M. K. Marichelvam

Ömür Tosun

View Times: 90

Update Date: 15 Jan 2024

Table of Contents

Video Upload Options

Confirm