Neuromorphic Photonic Integrated Circuits

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Muhammad Ali Butt	--	7472	2024-01-09 07:58:26	\|
2	layout & references	Sirius Huang	Meta information modification	7472	2024-01-10 02:04:40	\|

This entry is adapted from the peer-reviewed paper 10.3390/nano13243139

Neuromorphic photonics is a cutting-edge fusion of neuroscience-inspired computing and photonics technology to overcome the constraints of conventional computing architectures. Its significance lies in the potential to transform information processing by mimicking the parallelism and efficiency of the human brain. Using optics and photonics principles, neuromorphic devices can execute intricate computations swiftly and with impressive energy efficiency. This innovation holds promise for advancing artificial intelligence and machine learning while addressing the limitations of traditional silicon-based computing.

neuromorphic computing photonic integrated circuit imaging artificial intelligence machine learning

1. Introduction

Neuromorphic photonics represents a cutting-edge, multidisciplinary realm at the confluence of artificial intelligence (AI), photonics, and neuroscience ^[1]. Its overarching goal is nothing short of a transformative evolution in computing, seamlessly uniting the foundational principles of neuromorphic computing with the swiftness and efficiency inherent in photonics ^[2]. This inventive paradigm employs light-based neurons and optical synapses to emulate the intricate behaviors of human brain cells closely, resulting in specialized hardware uniquely tailored for the domains of AI and machine learning ^[3]. The standout feature of this field is its remarkable energy efficiency, enabling lightning-fast, parallel data processing while conserving power resources. By harnessing the velocity of light and mirroring the intricate neural networks (NNs) of the human brain, neuromorphic photonics has the potential to unlock entirely novel horizons in high-performance computing, poised to dramatically elevate applications in pattern recognition, data manipulation, and intricate problem-solving ^[4]^[5]. While still in its infancy, this field holds promise of more capable and efficient AI systems, with the potential to fundamentally reshape the computing landscape ^[6].

AI technologies, encompassing facial recognition, machine learning, and autonomous driving, are reshaping our daily lives ^[7]^[8]. Deploying of task-specific AI systems demands training NNs with extensive datasets on conventional computers. However, limitations in throughput and efficiency due to prevailing computer architectures currently hinder this process ^[9]. Drawing inspiration from the intricate architecture of the human brain, researchers are pioneering the development of next-generation intelligent computing systems designed to emulate synapses and neurons. These systems encode information using spatiotemporal pulse patterns generated by presynaptic neurons, with postsynaptic neurons accumulating and generating new neuronal pulses upon reaching stimulation thresholds. By integrating myriad neurons, these systems give rise to nonlinear spiking NNs, enabling information processing through spatiotemporally encoded neuron pulses. Intel’s TrueNorth chips, for instance, have achieved a remarkable level of energy efficiency, surpassing conventional microelectronic chips for specific AI tasks and rivaling the computational capabilities of the human brain ^[10]. Nevertheless, the scalability of integrated neurons remains hampered by challenges such as electrical interconnect bandwidth, pulse loss, and communication delays. Optical interconnects, offering substantial bandwidth, minimal loss, and negligible latency, have the potential to address these electrical interconnect limitations ^[11].

The demands of real-time, data-intensive, intelligent information processing tasks underscore the need for innovative and smart optimization hardware. Convolutional neural networks (CNNs) excel at extracting hierarchical feature maps to enhance recognition accuracy, and there is a growing interest in employing photonics for their implementation. In this context, a large-scale and adaptable photonic convolutional neural network (PCNN) that leverages a hardware-friendly distributed feedback laser diode (DFB-LD) is proposed ^[12]. This approach involves applying a biological time-to-first-spike coding method to a DFB-LD neuron to execute temporal convolutional operations (TCO) for image processing. In practical experiments, PCNN successfully employs TCO to extract image features using 11 × 11 convolutional kernels. Additionally, the temporal pulse shaping of a DFB-LD neuron is explored to construct a densely connected and fully connected layer, enabling rapid adjustments of synaptic weights at a remarkable rate of 5 GHz and providing high classification accuracy in benchmark image classification tasks, with 98.56% for MNIST and 87.48% for Fashion-MNIST. These findings underscore the potential of optical analog computing platforms resembling neurons for real-time and intricate intelligent processing networks ^[13].

2. Neuromorphic Photonic Integrated Circuits

With the recent emergence of Photonic Integrated Circuit (PIC) technology platforms, the timing is perfect for developing scalable, fully reconfigurable systems capable of executing vastly more complex operations than ever before ^[14]. While numerous fields, such as microwave photonics and physical layer security, stand to benefit significantly from this rapid increase in complexity, the community has yet to establish a universal processing standard for programming intricate multistage operations within the photonic domain. Neuromorphic photonics is an exciting and emerging field at the intersection of neuroscience and photonics. This groundbreaking discipline harnesses the efficiency of NNs and the lightning-fast capabilities of photonics to create processing systems that can outperform microelectronics by orders of magnitude. Thanks to their partial analog nature, neuromorphic circuits can leverage optical signals’ vast bandwidth and energy efficiency. Additionally, they set the stage for a comprehensive processing standard for reconfigurable circuits capable of theoretically executing any task that an artificial NN can compute. Integrating these systems with low-power microelectronic control promises processing efficiencies that surpass current digital standards by a considerable margin. In essence, the emergence of PIC technology, coupled with the advent of neuromorphic photonics, heralds a new era of computing where the potential for innovation and efficiency is boundless.

To transcend the constraints imposed by traditional microelectronic computing, it is imperative to incorporate unconventional techniques that leverage new processing methodologies. PICs offer a promising avenue to address these limitations, and several factors underscore their suitability. Firstly, photonic interconnects present a direct solution to the data transport quandary: a substantial portion of energy consumption on modern microelectronic chips is attributed to metal wires’ constant charging and discharging. This energy overhead can be circumvented by using on-chip photonic links, especially as optical devices advance in efficiency ^[15]. Secondly, photonic systems can harness optical multiplexing and high-speed signals to achieve an impressive bandwidth density. This translates into a remarkable computational density (operations per second per square millimeter, ops/s/mm²) for closely spaced waveguides or filters that perform densely packed operations ^[16].

Furthermore, implementing linear operations like Multiply-Accumulate (MACs) in the photonic realm inherently consumes minimal energy, yielding a highly advantageous, sublinear scaling of energy consumption concerning the number of operations conducted ^[17]. The combination of these three properties can deliver substantial enhancements in performance, encompassing energy efficiency and computational density, as illustrated in Figure 1.

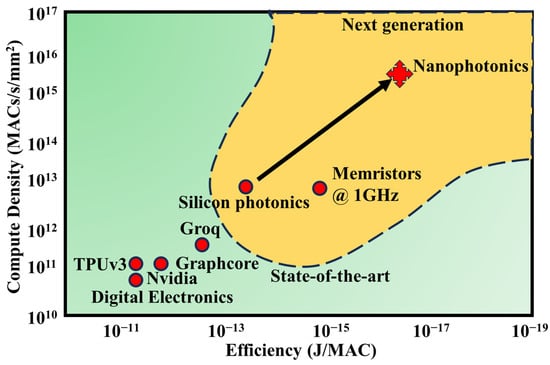
Figure 1. A comparison between specialized deep-learning digital electronic architectures and silicon photonic and nanophotonic platforms. In this context, photonic systems can support high on-chip bandwidth densities while maintaining low energy consumption during data transmission and computational tasks. The metrics for electronic architectures have been sourced from various references ^[18]^[19]^[20]^[21]. The metrics for silicon photonic platforms are estimated based on a contemporary silicon photonic setup operating at 20 GHz, comprising 100 channels with tightly packed micro rings. Meanwhile, the nanophotonic metrics are derived from the assumption of closely packed athermal microdisks ^[22], each occupying an area of approximately 20 µm, running at 100 GHz and operating close to the shot noise limit. Inspired by ^[14].

Neuromorphic photonic systems have demonstrated processing speeds 6–8 orders of magnitude higher than their electronic counterparts ^[23]. Silicon photonics, an optoelectronic integration technology compatible with well-established microelectronics, harmonizes the ultra-large-scale logic and precision manufacturing attributes of CMOS technology with the high-speed and low-power consumption benefits of photonic technology, effectively reconciling the conflict between technological advancement and cost constraints. In recent years, on-chip NNs based on silicon photonic technology have made significant strides ^[24]. In 2017, Shen et al. showcased an on-chip NN employing a silicon-based Mach–Zehnder interferometer structure capable of recognizing fundamental vowels ^[17]. In this architecture, an external subsystem configures the matrix element values for vector-matrix multiplication using Mach–Zehnder interferometer (MZI) structures. To modify these values during optimization, signals must be relayed from the NN to the control system. Tait et al. introduced on-chip variable weight synapses based on silicon electro-optical modulators in 2016 ^[25], as well as on-chip neurons relying on silicon electro-optical modulators in conjunction with off-chip multi-wavelength lasers, wavelength division multiplexers/demultiplexers, and on-chip photodetectors in 2019 ^[26]. This innovative structure facilitates weight adjustments by modulating the silicon microring with electrical signals and regulates the silicon microring modulator to achieve neuron functionality through electrical signals derived from on-chip detector optoelectrical conversion.

Neuromorphic PICs on silicon platforms have witnessed remarkable advancements in recent times ^[23]^[27]^[28]^[29]. These photonic NNs (PNNs), even in their early stages with a limited number of neurons, have showcased their prowess in high-bandwidth, low-latency machine-learning signal processing applications. The next frontier in this domain involves the quest for large-scale PNNs endowed with flexibility and scalability, positioning them to tackle data-intensive machine learning (ML) applications with high-speed requirements. In ^[30], architectural foundations are proposed, focusing on microring resonator (MRR)-based photonic neurons, both non-spiking and spiking, and the orchestration of PNNs through a broadcast-and-weight approach. A novel expansion of NN topologies by cascading photonic broadcast loops is discussed, culminating in a scalable NN structure with consistent wavelengths. Moreover, incorporating wavelength-selective switches (WSS) within these broadcasting loops is proposed, delivering the concept of a wavelength-switched photonic NN (WS-PNN). This innovative architecture opens new doors for integrating off-chip WSS switches, enabling the interconnection of photonic neurons in versatile combinations, delivering unmatched scalability for PNNs, and accommodating an array of feedforward and recurrent NN topologies.

2.1. Deep DNNs

Deep neural networks (DNNs) have gained prominence due to advancements in processing power and the ubiquity of data. Faster and more affordable computing resources have facilitated rapid convergence, making deep learning (DL) more accessible. The widespread availability of data, along with improved algorithms, enhances the value of these networks, especially in applications like chatbots for businesses ^[31]^[32]. These networks, however, demand substantial computational power and extensive data sets. They excel in scenarios where ample data is available and where it is feasible to categorize or rank preferred outcomes ^[4].

DNN represents a sophisticated machine learning (ML) technique that empowers computers, through training, to accomplish tasks that would be exceedingly challenging with traditional programming methods ^[33]. The inspiration for NN algorithms is drawn from the human brain and its intricate functions. Like the human mind, DNNs are designed not to rely solely on predetermined rules but to predict solutions and draw conclusions based on previous iterations and experiences. A NN consists of multiple layers of interconnected nodes that receive input from previous layers and generate an output, ultimately reaching a final result. NNs can encompass various hidden layers, and the complexity increases with adding more layers. Here are distinct neural network architectures (Figure 2):

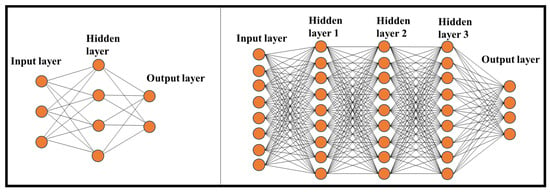
Figure 2. Traditional NN (left) versus DNN (right).

(A): Traditional NNs: Typically composed of 2 or 3 hidden layers.
(B): DL Networks: These can contain up to 150 hidden layers, making them significantly more complex.

A DNN is considerably more intricate than a “simple” NN. A standard NN operates akin to a chess game, adhering to predefined algorithms. It offers different tactics based on inputs from the programmer, such as how chess pieces move, the size of the chessboard, and strategies for various situations. However, a NN transcends this input-bound behavior and can learn from past experiences, evolving into a DNN. For instance, on the same computer, you can train an NN, play games against other individuals, and enable it to learn as it engages in these matches. As it learns from various players, defeating a DNN, even for chess masters, might become exceedingly challenging or even insurmountable. DNNs can recognize voice commands, identify voices, recognize sounds and graphics, and accomplish a wide array of tasks beyond the capacity of traditional NNs. They leverage “big data” along with sophisticated algorithms to tackle complex problems, often requiring minimal to no human intervention.

Understanding the process of a DNN is best illustrated through a practical example. Imagine you have an extensive collection of hundreds of thousands of images, some of which feature dogs, and you aim to create a computer program to identify dogs in these pictures. At this point, you face a crucial decision. You can either write a program explicitly designed to identify dogs or opt for a more intelligent approach—a program that “learns” how to recognize dogs. Initially, you might choose the former option, but this turns out to be a less-than-ideal choice. Conventional programming techniques require a laborious and intricate process, and the outcomes often lack the desired accuracy. To explicitly identify dog pictures, you must create a software program filled with conditional “if” and “then” statements. This program would elevate the probability of a dog’s presence whenever it detects a dog-like attribute, such as fur, floppy ears, or a tail.

Convolutional neural networks (CNNs) represent a subset of AI explicitly designed to handle and learn from vast datasets. These networks are aptly named due to their distinctive architecture and purpose. CNNs excel in image recognition and perform not only generative but also descriptive tasks. Generative tasks encompass various activities such as auto-cropping, caption generation, video processing, mimeographing, and image overlays. A vital component of a CNN is the convolutional layer, where each neuron processes information from a small portion of the visual field, with their inputs forming a checksum-like pattern to create feature maps.

Artificial neural networks (ANNs) are interconnected perceptrons organized into various layers. ANNs are often called Feedforward Neural Networks, as they process inputs linearly, forwarding the results through the network layers. These networks are known as universal function approximators, capable of learning any function, and their versatility is attributed, in part, to activation functions. These functions introduce nonlinearity into the network, enabling it to learn intricate relationships between inputs and outputs and promoting cooperative learning among network parts. It is important to note that the logic behind neural networks is often incomprehensible to humans. Deep learning models operate as black boxes, with hidden layers of nodes creating complex, interconnected logic. Some attempts have been made to visualize the logic behind NNs for image recognition, but this is not always possible, especially for demanding tasks.

2.2. NNs with Complex Arithmetic Calculations

While computers excel at performing complex calculations, the realm of solving mathematical problems continues to present a significant challenge for artificial intelligence ^[34]. This challenge can be viewed from two distinct angles. On the one hand, grounding structured mathematical knowledge into a framework of intrinsic meaning has persisted as a longstanding issue in symbolic AI ^[35]. On the other hand, NNs have traditionally struggled to acquire mathematical proficiency, as their nature primarily hinges on statistical pattern recognition abilities rather than the explicit application of syntactic rules ^[36]. The process of mathematical reasoning poses well-documented hurdles for connectionist models. Mathematical formulas employ symbols that often appear as arbitrary tokens, necessitating manipulation under well-defined rules that involve compositionality and systematicity. Furthermore, extracting mathematical knowledge from examples should extend beyond the observed data distribution, facilitating the ability to extrapolate by discovering fundamental ‘first principles’.

Notwithstanding these formidable challenges, recent breakthroughs in DL have sparked a renewed enthusiasm for the notion that NNs may attain advanced reasoning capabilities, consequently displaying symbolic behavior ^[37]. Although deep networks have historically grappled with fundamental concepts such as the understanding of ‘integer numbers’ ^[38], the last few years have witnessed the emergence of several models that showcase remarkable proficiency in tackling intricate mathematical tasks.

For instance, sequence-to-sequence architectures have demonstrated their ability to learn the intricacies of function integration and the resolution of ordinary differential equations, occasionally outperforming even widely used mathematical software packages in terms of accuracy ^[39]. DL models have further made notable inroads in the realm of automated theorem proving ^[40] and have actively supported expert mathematicians in the formulation of conjectures and the establishment of pioneering results in the realm of pure mathematics ^[41].

In remarkable developments from last year, deep reinforcement learning uncovered a more efficient algorithm for performing matrix multiplication ^[42], while fine-tuning a pre-trained language model on computer code enabled the resolution of university-level mathematical problems at a level comparable to human expertise ^[43]. These achievements herald a promising new era where neural networks may bridge the gap between mathematical reasoning and machine learning, potentially unlocking new frontiers in artificial intelligence.

These outstanding accomplishments owe much to the advent of meticulously curated, expansive datasets encompassing mathematical problems and their corresponding solutions. Furthermore, they owe their success to inventing novel, sometimes ad hoc, architectures tailored to more effectively process numerical symbols and mathematical notations. In addition, strides in many tasks have been propelled by creating large-scale language models, which exhibit astonishing innate numerical capabilities ‘out of the box’, that can be further honed through fine-tuning and strategic prompting techniques.

However, it is imperative to emphasize that these achievements do not necessarily equate to a full grasp of the semantics underlying numbers and basic arithmetic by these models. Their performance on relatively straightforward numerical tasks often reveals fragility, signaling a need to enhance their foundational mathematical skills to establish a more dependable foundation for mathematical capabilities. This notion finds support in a wealth of literature on child development and education, which underscores the significance of fundamental numeracy skills such as counting, quantity comparison, comprehension of number order, and mastery of the base-ten positional numeral system as robust predictors of later mathematical achievement ^[44].

The quest for solutions to matrix eigenvalues has perpetually been a focal point of contemporary numerical analysis, with profound implications for the practical application of engineering technology and scientific research. While extant algorithms for matrix eigenvalue computation have made considerable progress in computational accuracy and efficiency, they have struggled to find a foothold of photonic platforms. Enter the PNN, a remarkable fusion of potent problem-solving capabilities and the inherent advantages of photonic computing, characterized by its astonishing speed and minimal energy consumption. In ^[45], an innovative approach introduces an eigenvalue solver tailored for real-value symmetric matrices, leveraging reconfigurable PNNs. This strategy demonstrates the practicality of solving eigenvalues for n × n real-value symmetric matrices using locally connected networks. In a groundbreaking series of experiments, the capacity to solve eigenvalues for 2 × 2, 3 × 3, and 4 × 4 real-value symmetric matrices through the deployment of graphene/Si thermo-optical modulated reconfigurable photonic neural networks featuring a saturated absorption nonlinear activation layer was showcased. Theoretical predictions indicate a remarkable test set accuracy of 93.6% for 2 × 2 matrices, with experimental results achieving a measured accuracy of 78.8%, aligning with standardized metrics for easy comparison. This work not only charts a course for on-chip integrated photonic solutions to eigenvalue computation for real-value symmetric matrices but also forms the bedrock for a new era of intelligent on-chip integrated all-optical computing. This breakthrough promises to transform the landscape of computational methodologies, ushering in a future where photonic platforms play a pivotal role in numerical problem-solving across various domains ^[45].

The objective of the proposed PNN is to address the challenge of computing eigenvalues for symmetric matrices. This problem frequently arises in the context of various physical scenarios (as shown in Figure 3a). The initial focus centers on solving the eigenvalue problem for 2 × 2 symmetric matrices characterized by non-negative real-value elements and eigenvalues. Furthermore, the matrix elements were confined within the range of 0 to 10. This limitation does not constrain the network’s performance, as any other matrices can be derived through linear scaling from a matrix within this constrained domain. Crucially, this network is adaptable and designed to handle the eigenvalue problem for n × n matrices under similar conditions. This versatility allows it to be employed in diverse scenarios, offering a powerful tool for eigenvalue computation in various applications.

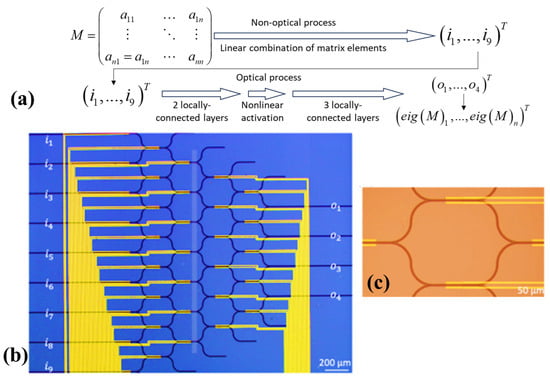
Figure 3. Conceptual framework of the newly proposed photonic neural network. The essential steps involved in achieving the desired task (a), an optical micrograph showcasing the distinctive structure of the proposed network, featuring nine input ports (i₁–i₉) and four output ports (o₁–o₄) ^[45] (b), an optical micrograph that zooms in on a single cell within the network, housing two phase shifters and a merging structure ^[45] (c).

The structure of the PNN is characterized by an architectural design that includes a single linear fully connected layer, complemented by a sophisticated five-layer locally connected arrangement. This network boasts nine input and four output ports, as Figure 3b depicts. The five-layer structure is a critical component of the described architecture, characterized by an intricate arrangement of neurons. In the first layer, eight neurons are featured, each sharing a phase shifter with its neighboring unit (as illustrated in Figure 3c).

The next layer comprises seven neurons, with each successive layer reducing the count by one, resulting in 35 tunable weights. Additionally, the researchers introduced two extra weights for training. The first weight pertains to the input light’s intensity, denoting the intensity ratio. This factor is crucial as the nonlinear activation function behaves differently under varying intensities. The second weight governs the output ratio, linearly adjusting the relationship between output intensity and the corresponding eigenvalue, effectively establishing the output ratio. This adjustment is essential because, unlike electronic neural networks, optical layers cannot manipulate light intensity freely and directly. Consequently, the absolute value of the output signal may not align with the scale provided in the dataset.

Photonic circuits have also found their applicability in complex-valued neural networks ^[46]^[47]^[48]. The articles ^[46]^[47] presented neural network architectures that use complex arithmetic computations and a MZI to encode information in both phase and amplitude (Figure 4a,b). This approach allows complex arithmetic to be performed using the properties of interference. The resulting complex-valued ONCs (optical neural chips) perform better on several tasks than their counterparts in single-neuron and deployed network implementations. A single complex-valued neuron can solve some nonlinear problems that a real-valued analog cannot compute. There are many comparative analyses, tests, and trainings of the NN on various datasets. The data obtained suggest that this architecture uses double the number of trained free parameters, and can classify nonlinear patterns with simple architectures (fewer layers). Research results have shown that these architectures significantly improve the speed and accuracy of computation compared to traditional real-valued circuits.

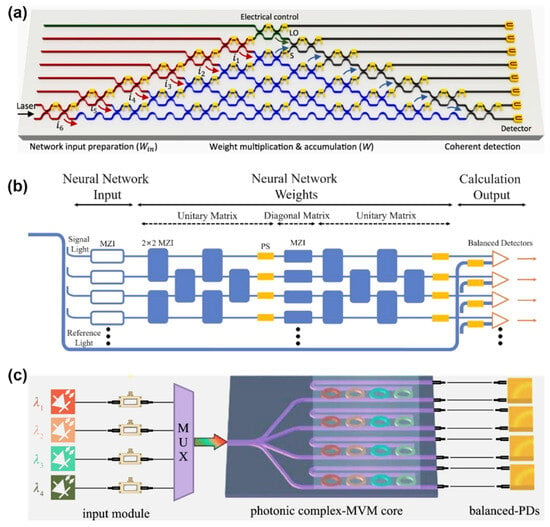
Figure 4. The developed architectures of complex-valued optical neural architectures using: (a,b) MZIs, the circuits themselves realize a multiport interferometer with phase shifters (PSs) inserts used for phase tuning ^[46]^[47]; (c) MRRs for matrix-vector multiplication (MVM) applications using WDM ^[48].

The application of MRR arrays in complex-valued neural networks is also possible, as demonstrated in ^[48]. To realize the transition from real values to complex-valued data, an approach with a pre-decomposition of the input matrix (the values are supplied to beams with different wavelengths employing optical intensity modulators) and the transmission matrix (controlled by selection of values utilizing heaters on the resonator rings) (Figure 4c) is used in this work. A balanced photodetector registers the result of the multiplication of the two matrices. This approach allowed the realization of other mathematical transformations, including discrete Fourier transform (DFT) and convolutional image processing. The results of the experiments in both signal and image processing unequivocally show that the newly proposed system can expand matrix computation to include real numbers, full complex numbers, higher processing dimensions, and convolution. Consequently, the processor can function as a versatile matrix arithmetic processor capable of handling intricate tasks in different scenarios. The researchers note that improved system performance can be obtained by adding parallel computation with WDM and increasing the degree of integration of the circuit components.

2.3. Spike NNs

Over the past decade, ANNs have made remarkable strides, progressing from the initial multi-layer perceptron (MLP) of the first generation to the cutting-edge techniques of the second-generation DNNs ^[49]^[50]. This advancement has been significantly fueled by abundant annotated data and the widespread availability of high-performance computing devices, including versatile Graphics Processing Units (GPUs). However, even with these achievements, ANNs still fall short of matching biological neural networks’ (BNN) energy efficiency and their online learning capabilities. Many endeavors have been undertaken to diminish the power consumption of conventional deep-learning models. These efforts aim to uncover more streamlined networks that deliver similar performance with reduced complexity and fewer parameters than their original counterparts. Several techniques have been developed for this purpose, including quantization ^[51], pruning ^[52], and knowledge distillation ^[53]. Quantization involves converting the network’s weights and inputs into integer types, thereby lightening the overall computational load. Pruning entails the iterative removal of connections within a network during or after training to compress the network without compromising performance. Knowledge distillation transfers the intricate knowledge acquired by a high-complexity network, the teacher, to a lightweight network known as the student.

While ANNs and DNNs have traditionally been inspired by the brain, they fundamentally differ in structure, neural computations, and learning rules compared to BNNs. This realization has led to the emergence of spiking neural networks (SNNs), often regarded as the third generation of NNs, offering the potential to surmount the limitations of ANNs. The utilization of SNNs on neuromorphic hardware like TrueNorth ^[54], Loihi ^[55], SpiNNaker ^[56], NeuroGrid ^[57], and others presents a promising solution to the energy consumption predicament. In SNNs, similar to BNNs, neurons communicate via discrete electrical signals known as spikes and operate continuously in time. Due to their functional resemblance to BNNs, SNNs can exploit the sparsity inherent in biological systems and are highly amenable to temporal coding ^[58]. While SNNs may still trail behind DNNs regarding overall performance, this gap is narrowing for specific tasks. Notably, SNNs typically demand considerably less energy for their operations. Nevertheless, training SNNs remains challenging due to the intricate dynamics of neurons and the non-differentiable nature of spike operations.

2.4. Convolutional Neural Networks (CNNs)

CNNs are inherently feedforward networks, exhibiting unidirectional information flow, transmitting data exclusively from inputs to outputs. As ANNs draw inspiration from biological systems, CNNs share a similar motivation. Their architecture is heavily influenced by the brain’s visual cortex structure, characterized by layers of simple and complex cells ^[59]^[60]. CNN architectures offer a range of variations yet generally comprise convolutional and pooling (subsampling) layers organized into distinct modules. These modules are subsequently followed by one or more fully connected layers, resembling a conventional feedforward NN. Often, these modules are stacked to create deep models. Figure 5 illustrates typical CNN architecture for a simplified image classification task, where an image is initially fed into the network and undergoes several convolution and pooling stages. The representations obtained from these operations are then channeled into one or more fully connected layers. Finally, the last fully connected layer provides the output as a class label. While this architecture remains the most prevalent in the literature, various changes have been proposed in recent years to enhance image classification accuracy or economize on computation costs.

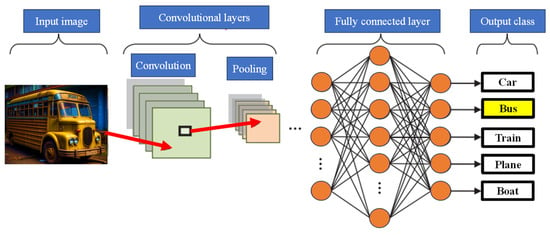
Figure 5. CNN image classification pipeline.

CNNs represent a revolutionary paradigm shift in image recognition, enabling the detection and interpretation of intricate patterns within visual data ^[61]. Their effectiveness is unrivaled, positioning them as the preeminent architecture for image classification, retrieval, and detection tasks, delivering results characterized by exceptional accuracy. The versatility of CNNs extends to real-world scenarios, where they consistently yield high-quality results. They excel in localizing and identifying objects, be it a person, a car, a bird, or any other entity within an image. This adaptability has made CNNs the default choice for predictive image input tasks. A fundamental attribute of CNNs is their capacity to attain ‘spatial invariance’. This signifies their ability to autonomously learn and extract image features from any location within the image, obviating the need for manual feature extraction. CNNs draw these features directly from the image or data, underscoring their potency within the realm of DL and their remarkable precision. As elucidated in ^[62], the purpose of pooling layers is to reduce the spatial resolution of feature maps, thereby achieving spatial invariance to input distortions and translations. Pooling layers streamline image processing and enhance computational efficiency by reducing the number of required parameters, resulting in expedited data processing. This reduction in memory demands and computational costs bolsters the appeal of CNNs. While CNNs have prominently left their mark on image analysis, their scope extends well beyond this domain. They can be applied to diverse data analysis and classification challenges. This adaptability spans various sectors, yielding precise outcomes in face recognition, video classification, street and traffic sign recognition, galaxy classification, and the interpretation and diagnosis of medical images, among others ^[63]^[64]^[65].

2.5. Methods for Implementing the Activation Functions in Optical Neural Networks

AI has become instrumental across diverse applications. Nevertheless, AI systems traditionally demand substantial computational resources and memory. The diminishing returns of Moore’s law have signaled a shift away from conventional architectures for AI algorithms, as referenced in ^[66]. Furthermore, the pressing need for power-efficient implementations of ANNs has surfaced, particularly in scenarios like image recognition, where processing a single image may entail billions of operations ^[67]. There is an active exploration into replacing or supplementing traditional integrated electronic circuits with photonic circuits. A pivotal facet of silicon photonics is WDM, which empowers the simultaneous transmission of multiple signals over a shared medium without interference. In Optical Neural Networks (ONNs), WDM facilitates parallel processing of multiple data streams simultaneously. ONNs promise to surpass their electronic counterparts in terms of both speed and energy efficiency. For instance, common operations like matrix multiplications are resource-intensive on conventional computers, but they can be executed at ultra-high speeds using specialized configurations of photonic networks ^[68]. All-optical ANNs, devoid of optoelectronics or electro-optical conversion other than the interface, enable matrix multiplications to occur at the speed of light as optical signals propagate through waveguides. Silicon photonics further allows the integration of photonic and electronic devices on the same platform ^[69].

In this context, two prominent optical modulators, Mach–Zehnder interferometers (MZIs) and microring resonators (MRRs), are commonly employed ^[70]^[71]. MZIs, although bulkier, exhibit resilience to process and temperature variations due to their signal processing method, which involves signal delay within one of the two branches. On the other hand, MRRs are more compact and rely on slight detuning of the resonant wavelength from the input signal to perform dot products. This approach enables WDM but introduces challenges related to the accurate calibration of the resonant rings, as their resonance can drift with temperature variations, leading to increased complexity and power overhead.

Replicating an ANN with an Optical Neural Network (ONN) presents a significant challenge, primarily revolving around the comprehensive optical implementation of every core module in a conventional ANN. While optical matrix multiplication has been successfully realized ^[72], the activation function (AF), a pivotal element in ANNs, remains a complex issue. The matrix multiplication stage corresponds to the linear transformation data undergo in an ANN. However, to achieve optimal results, a non-linear transformation is equally essential, typically performed by the AF. Existing contributions in this domain have taken different approaches. Some ONN implementations incorporate the AF through computer-based or partially electrical components. In contrast, others strive for full optical integration by utilizing optical non-linearities at either a material or device level. In the former approach, the optical circuit’s information is converted into electrical format for AF processing on a computer, and then the output is reconverted into the optical circuit. However, this method limits the network’s speed due to electronic circuit constraints, introducing noise that degrades accuracy. Moreover, this dual conversion process introduces considerable latency and higher power consumption, ultimately undermining the advantages of optical implementation.

Despite the introduced network delays and significant increases in power consumption and chip size, the O-E-O conversion remains the most common way to implement the activation function on a photonic chip. Since achieving nonlinearity of the characteristic only on photonic elements is a challenging task, many researchers are developing various combinations of photonic elements that can influence the characteristic for the necessary adjustment by electronic components. Also, solutions include using hybrid structures (Ge/Si hybrid structure in a micro-ring resonator) ^[73], structures using the free-carrier dispersion effect (scheme with a Mach–Zehnder interferometer loaded with MCR, heating elements, and a Mach–Zehnder coupler) ^[73]^[74]^[75] and another popular direction—phase change material (PCM) coatings ^[76]^[77]. The given examples can realize not one but several variants of activation functions: radial basis, sigmoid, softplus, Relu, and ELU. This increases the flexibility of these structures because, depending on the task solved by the neural network, different characteristics and threshold values of activation functions may be required.

Consequently, despite the promising results achieved by works that implement the AF electrically ^[78]^[79], it is believed that an optical AF is imperative to unlock the full potential of ONNs. Such an approach can mitigate the bottlenecks associated with electronic conversions and offer the speed, precision, and efficiency required to fully harness the capabilities of ONNs.

Nevertheless, the implementation of AFs in optical networks can diverge due to the inherent nature of optical computing. Several standard optical activation functions are employed in these systems. One approach involves Nonlinear Optical Activation; whereby optical components are deliberately engineered to demonstrate nonlinear behavior. Notable examples include the Kerr effect and cross-phase modulation, both of which enable the creation of nonlinear optical activations by nonlinearly modulating the intensity of the light field ^[80]. Optical bistability is another avenue, employing optical bistable devices as activation functions. These devices exhibit two stable states and can be manipulated by adjusting input power or other optical parameters, thus serving as activation elements ^[81]. Optical switches come to the fore in the realm of all-optical Switches ^[82]. These switches can be deployed to execute binary-like activation functions by altering the optical signal’s path or state based on input intensity, rendering them well-suited for binary activations within optical neural networks. MZIs represent yet another option, capable of generating optical interference patterns sensitive to input intensity ^[83]. Through controlled phase shifts in the interferometer, they can be harnessed to perform activation functions. Nonlinear crystals offer a different route, enabling the creation of optical parametric amplifiers and oscillators and introducing nonlinear activation functions within photonic neural networks ^[84]. Lastly, resonators like ring resonators can be incorporated as activation functions, capitalizing on their resonance properties and input power levels ^[85].

The choice of an optical activation function in photonic neural networks hinges on the specific architectural design, hardware components, and the intended network characteristics. These optical activation functions are engineered to carry out nonlinear operations on optical signals, mirroring the behavior of digital activation functions found in conventional neural networks. Optical neural networks remain an active arena of research, continually producing novel techniques for implementing optical activation functions.

2.6. Programmable PNNs

The rapid and explosive growth of AI and Deep Learning (DL), coupled with the maturation of photonic integration, has opened a new realm of possibilities for optics in computational tasks ^[86]^[87]. Applying photons and advanced optical technologies in Neural Network (NN) hardware holds immense promise. It is projected to substantially increase Multiply-Accumulate (MAC) operations per second compared to traditional NN electronic platforms. Computational energy efficiency is estimated to plummet below the femtojoule (fJ) per MAC mark, while the area efficiency is anticipated to soar beyond millions of MAC operations per square millimeter ^[88]^[89]. This paradigm shift in NN hardware seeks to leverage the high data transmission rates enabled by integrated photonic technologies while also harnessing the compact size and low power consumption capabilities inherent to chip-scale designs. Up until now, the predominant focus in photonic devices designed for weight calculations has centered around elements that can be slowly reconfigured, such as Thermo-Optic (T/O) phase shifters ^[47] and Phase-Change Material (PCM)-based non-volatile memory structures ^[86]. This emphasis on slow reconfiguration implies that inference applications currently take precedence in neuromorphic photonics ^[23].

Extending reconfiguration capabilities to Photonic (P)-NN implementations demands a platform that can accommodate various functional layouts within the same neural hardware. Over the past few years, the realm of photonics has made significant strides in programmability ^[90], and programmable PICs ^[91] have emerged as a pivotal resource for fostering cost-effective, versatile, and multifunctional photonic platforms, akin to the concept of electronic Field-Programmable Gate Arrays (FPGAs) ^[90]. Furthermore, it has been demonstrated that merely incorporating slowly reconfigurable Mach–Zehnder Interferometric (MZI) switches within a suitable architectural framework can provide a plethora of circuit connectivity and functional possibilities ^[90]. Nonetheless, the unique characteristics of NN architectures necessitate the exploration of alternative functionalities yet to be covered by programmable photonic implementations. While contemporary photonic weighting technology can indeed facilitate weight value reconfiguration ^[17], there is a growing shift towards considering programmable activation functions ^[92]. Nevertheless, it is essential to note that existing neuromorphic photonic architectures lack reconfiguration mechanisms for their linear neuron stages. Photonic Neural Networks (PNNs) have mainly advanced within two primary architectural categories for implementing linear neural layers. The first category involves incoherent or Wavelength-Division-Multiplexed (WDM) layouts, where each axon within the same neuron is assigned a distinct wavelength ^[93]. The second category centers on coherent interferometric schemes, in which a single wavelength is utilized throughout the entire neuron, harnessing interference between coherent electrical fields to perform weighted sum operations.

An innovative architecture is proposed in ^[94] that seamlessly integrates WDM and coherent photonics to empower Programmable Photonic Neural Networks (PPNNs) with four distinct operational modes for linear neural layers. Building upon their previously proposed dual-IQ coherent linear neuron architecture ^[95], which recently demonstrated remarkable computational performance as a PIC with groundbreaking compute rates per axon ^[96], their next step is advancing single neuron architecture. This approach involves harnessing multiple wavelength channels and corresponding WDM De/Multiplexing (DE/MUX) structures to create multi-element and single-element fan-in (input) and weight stages for each axon. Programmability is achieved by integrating Mach–Zehnder Interferometer (MZI) switches, which can dynamically configure the connections between fan-in and weighting stages, offering the flexibility to define neural layer topologies through software.

A comprehensive mathematical framework for this programmable neuromorphic architecture was established and delved into a thorough analysis of potential performance limitations associated with using multiple wavelengths within the same interferometric arrangement. These findings led to a straightforward mechanism to mitigate wavelength-dependent behaviors in modulators and phase shifters at the fan-in and weighting stages. As a result, this programmable layout consistently delivers exceptional performance across all four distinct operational modes, ensuring that supported neurons always maintain a relative error rate lower than a specified threshold, provided that inter-channel crosstalk remains within the typical range of values below a certain threshold.

Figure 6a ^[94] depicts the fundamental structure of the neural layer. Instead of a single Continuous Wave (CW) input optical signal, M multiplexed CW signals are each centered at λ_m and dedicated to an independent virtual neuron. The input and weight modulators have been replaced by more intricate modulator banks, as illustrated in Figure 6c,e. Software-controlled switches enclose these modulator banks. The multichannel input signal is divided into two portions in the initial stage. One portion is directed to the bias branch, while the remaining part enters the Optical Linear Algebraic Unit (OLAU). Within the OLAU, the signal undergoes further splitting, with equal power distribution achieved by a 1-to-N splitter, an example of which is provided in Figure 6b. Subsequently, after being appropriately modulated by inputs (x_n,m) and weighted by (w_n,m), the signal is routed to the N-to-1 combiner, as depicted in Figure 6d ^[94]. At this juncture, the output signal interferes with the bias signal within a 3 dB X-coupler and is then directed to the DEMUX to generate the outputs (y_m). In the final step, each channel (m) undergoes algebraic addition of the weighted inputs with a designated bias. This results in a total of M independent N-fan-in neurons.

Many cutting-edge programmable photonic circuits leverage the remarkable capabilities of Mach–Zehnder interferometers (MZIs). MZIs offer precise control over power splitting ratios and relative phase shifts between input and output ports, achieved by adjusting the phase-shifting control elements using either thermo-optic or electro-optic effects. Through the strategic combination of multiple directional couplers and phase shifters within specific mesh configurations ^[97]^[98], MZI-based architectures can perform a diverse array of linear transformations across various ports. When complemented by optic-electro-optic nonlinearity ^[17] or optical-modulator-based reprogrammable nonlinearity ^[99], MZI-based architectures have proven their mettle in tackling intricate machine learning tasks, boasting superior processing speeds. Nevertheless, in the pursuit of significant phase tuning ranges, MZIs demand relatively high driving voltages ^[100], and the devices can extend up to around 100 μm in length. In large-scale on-chip integrated circuits designed for complex applications, two vital factors emerge as primary concerns: the device’s footprint and power consumption. A natural and promising avenue is the adoption of resonant structures that enhance light-matter interactions, thereby reducing device footprint, driving voltages, and overall power consumption ^[100].

Among these, MRRs have garnered attention for their ability to program real-valued weights through a ‘broadcast-and-weight’ protocol ^[101], resembling a continuous-time recurrent neural network ^[27]. A notable advancement involves programming weights at the interconnected waveguides between two MRRs using phase-change materials. This innovation has led to the development of a photonic tensor core, serving as a robust dot-product engine ^[102]. It is worth mentioning that most prior proposals employing MRRs primarily relied on wavelength-division multiplexing for input signals, and incoherently aggregated signals at the photodetectors. The potential of coherence networks, which harness the wave nature of electromagnetic fields, holds promise for novel advancements in the design of optical neural networks ^[47].

A groundbreaking coherent optical neural network architecture built upon MRRs is proposed in ^[103]. This innovative approach offers notable advantages regarding device footprint and energy efficiency compared to conventional optical neural networks based on Mach–Zehnder interferometer (MZI) architectures. This architecture’s linear matrix multiplication layer is fashioned by linking multiple linear units, each comprising a serially coupled double-RR ^[104] for harmonizing signals from different ports and a single-RR for precise phase adjustments. Incorporating element-wise activation at each port, this nonlinear unit is crafted using microring modulators and electrical signal processing, granting the flexibility to program diverse nonlinear activation functions. Notably, the linear and nonlinear components presented in this work maintain the coherency of input signals, thus constituting a complex-valued neural network ^[47]. Moreover, the inherent flexibility of this design enables the direct cascading of each layer on the same chip without the need for intermediate digital-to-analogue conversions. This reduces latency and minimizes energy waste associated with signal conversions. The input-output relationship in the designed architecture was illustrated through a transfer function, and automatic differentiation was employed ^[24]^[25] to train the tunable parameters directly. The design and training algorithms are not confined to the ring-based MRR design and can be adapted to various tunable systems. The network’s proficiency in information processing tasks was showcased to provide a concrete example of its capabilities, such as functioning as an Exclusive OR (XOR) gate and conducting handwritten digit recognition using the MNIST dataset ^[105].

In ^[103], ring-based programmable coherent optical neural network configuration is presented, as illustrated in Figure 6. Figure 6f,g are dedicated to the fundamental elements responsible for executing the linear transformation, described by the matrix 𝑊_𝑙. In contrast, Figure 6h represents the component running nonlinear activation functions. These components are constructed using waveguides that are intricately coupled to RRs. It is noteworthy that in this design, all RRs maintain a uniform diameter, while the separation distances between the rings and waveguides can be adjusted based on the specific functionality they serve.

Furthermore, this design operates under continuous wave conditions at a single operating frequency, denoted as ω₀. This characteristic enables us to exert precise control over the phase and amplitude of transmitted signals by adjusting the refractive index of each component. In essence, this allows for fine-tuning the neural network’s performance ^[103]. Figure 6i displays a waveguide’s transmission and phase responses of side-coupled with a ring as a function of phase detuning, Δϕ. These responses are shown for both the critically coupled and over-coupled scenarios. In the case of over-coupling, indicated by the components colored in green, these responses are utilized for phase-tuning purposes. On the other hand, the nonlinear activation ring, highlighted in blue, requires critical coupling to achieve a more extensive amplitude tuning range. Figure 6j presents an illustrative example of the transmission and phase response of the coupled double ring employed as a signal-mixing component. The key parameters involved here are the ring-waveguide coupling coefficient (𝑟𝑟𝑤) at 0.85, the ring-ring coupling coefficient (𝑟𝑟𝑟) at 0.987, and the single round trip amplitude transmission (𝑎) at 1 ^[103].

Figure 6. (a) An illustration of the PPNN. It consists of several components, including M laser diodes (LDs), a MUX, a 3dB X-splitter, a bias branch denoted as W_b, and a reconfigurable Optical Linear Algebra Unit (OLAU) ^[94]. The OLAU comprises a 1-to-N splitting stage, input (X_n) and weight (W_n) modulator banks, and an N-to-1 combiner stage. The output from the combiner stage interferes with the bias signal within a 3dB X-coupler and is then sent to a DEMUX. A closer examination reveals details of (b) 1-to-N splitting and (d) its N-to-1 coupling stage ^[94], (c) view of the bias branch, which includes wavelength-selective weights and phase modulators ^[94], (e) a closer look at an axon of the OLAU, which consists of switches for signal routing and modulators for inputs (x_n,m) and weights (w_n,m) ^[94], layout of a Single Layer Coherent Optical Neural Network ^[103] (f) a tunable all-pass single RR functions as a phase tuning component, (g) tunable serially-coupled double RRs are employed as signal mixing components between the ports, (h) the nonlinear activation unit transforms input signal 𝑥𝑛 into 𝑓(𝑥𝑛), where 𝑓 represents a nonlinear function (with 𝑛 = 3 in this example). The black ring within the nonlinear activation unit acts as a directional coupler, directing a portion of the optical energy (𝛼) for electrical signal processing. The diode is a photodetector, and the blue ring modulates the signal. An electronic circuit (M) processes the electronic output from the photodetector to generate a modulation signal for the right ring ^[103] (i) displays the transmission and phase responses of a bus waveguide side-coupled with a ring, showcasing variations as a function of phase detuning, Δϕ. Over-coupling, indicated in green, is employed for phase-tuning components. At the same time, critical coupling, highlighted in blue, is crucial for achieving a larger amplitude tuning range in the nonlinear activation ring ^[103], (j) provides an example transmission and phase response of the coupled double ring, used as a signal mixing component ^[103].

References

Schuman, C.D.; Kulkarni, S.R.; Parsa, M.; Mitchell, J.P.; Date, P.; Kay, B. Opportunities for Neuromorphic Computing Algorithms and Applications|Nature Computational Science. Nat. Comput. Sci. 2022, 2, 10–19. Available online: https://www.nature.com/articles/s43588-021-00184-y (accessed on 22 October 2023).
van de Burgt, Y.; Santoro, F.; Tee, B.; Alibart, F. Editorial: Focus on organic materials, bio-interfacing and processing in neuromorphic computing and artificial sensory applications. Neuromorphic Comput. Eng. 2023, 3, 040202.
Alagappan, G.; Ong, J.R.; Yang, Z.; Ang, T.Y.L.; Zhao, W.; Jiang, Y.; Zhang, W.; Png, C.E. Leveraging AI in Photonics and Beyond. Photonics 2022, 9, 75. Available online: https://www.mdpi.com/2304-6732/9/2/75 (accessed on 13 November 2023).
Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 1–74. Available online: https://journalofbigdata.springeropen.com/articles/10.1186/s40537-021-00444-8 (accessed on 25 October 2023).
Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81.
Das, R.R.; Reghuvaran, C.; James, A. Graphene-based RRAM devices for neural computing. Front. Neurosci. 2023, 17, 1253075.
Nassehi, A.; Zhong, R.Y.; Li, X.; Epureanu, B.I. Chapter 11-Review of machine learning technologies and artificial intelligence in modern manufacturing systems. In Design and Operation of Production Networks for Mass Personalization in the Era of Cloud Technology; Mourtzis, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 317–348.
Mukhamediev, R.I.; Popova, Y.; Kuchin, Y.; Zaitseva, E.; Kalimoldayev, A.; Symagulov, A.; Levashenko, V.; Abdoldina, F.; Gopejenko, V.; Yakunin, K.; et al. Review of Artificial Intelligence and Machine Learning Technologies: Classification, Restrictions, Opportunities and Challenges. Mathematics 2022, 10, 2552. Available online: https://www.mdpi.com/2227-7390/10/15/2552 (accessed on 13 November 2023).
Le, Q.V. Building high-level features using large scale unsupervised learning. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8595–8598.
Ríos, C.; Youngblood, N.; Cheng, Z.; Le Gallo, M.; Pernice, W.H.P.; Wright, C.D.; Sebastian, A.; Bhaskaran, H. In-memory computing on a photonic platform. Sci. Adv. 2023, 5, eaau5759.
Zhang, D.; Tan, Z. A Review of Optical Neural Networks. Appl. Sci. 2022, 12, 5338.
Zhang, J.; Ma, B.; Zhao, Y.; Zou, W. A Large-Scale Photonic CNN Based on Spike Coding and Temporal Integration. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 7600910.
Huang, C.; de Lima, T.F.; Tait, A.N.; Marquez, B.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic Photonics for Intelligent Signal Processing. In Proceedings of the 2021 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 18–21 October 2021; pp. 1–2.
Peng, H.-T.; Nahmias, M.A.; de Lima, T.F.; Tait, A.N.; Shastri, B.J.; Prucnal, P. Neuromorphic Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–15.
Du, W.; Wang, T.; Chu, H.-S.; Nijhuis, C.A. Highly efficient on-chip direct electronic–plasmonic transducers. Nat. Photonics 2017, 11, 623–627.
Prucnal, P.R.; Shastri, B.J.; Teich, M.C. (Eds.) Neuromorphic Photonics; CRC Press: Boca Raton, FL, USA, 2017.
Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446.
Accelerating Systems with Real-Time AI Solutions-Groq. Available online: https://groq.com/ (accessed on 22 October 2023).
Teich, P. Tearing Apart Google’s TPU 3.0 AI Coprocessor-The Next Platform. Available online: https://www.nextplatform.com/2018/05/10/tearing-apart-googles-tpu-3-0-ai-coprocessor/ (accessed on 22 October 2023).
Smith, R. NVIDIA Volta Unveiled: GV100 GPU and Tesla V100 Accelerator Announced. Available online: https://www.anandtech.com/show/11367/nvidia-volta-unveiled-gv100-gpu-and-tesla-v100-accelerator-announced (accessed on 22 October 2023).
Wijesinghe, P.; Ankit, A.; Sengupta, A.; Roy, K. An All-Memristor Deep Spiking Neural Computing System: A Step Toward Realizing the Low-Power Stochastic Brain. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 345–358. Available online: https://ieeexplore.ieee.org/document/8471280?denied= (accessed on 22 October 2023).
Timurdogan, E.; Sorace-Agaskar, C.M.; Sun, J.; Shah Hosseini, E.; Biberman, A.; Watts, M.R. An Ultralow Power Athermal Silicon Modulator. Nat. Commun. 2014, 5, 1–11. Available online: https://www.nature.com/articles/ncomms5008 (accessed on 22 October 2023).
Shastri, B.J.; Huang, C.; Tait, A.N.; de Lima, T.F.; Prucnal, P.R. Silicon Photonics for Neuromorphic Computing and Artificial Intelligence: Applications and Roadmap. In Proceedings of the 2022 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 25–29 April 2022; pp. 18–26.
Zhou, Z.; Chen, R.; Li, X.; Li, T. Development trends in silicon photonics for data centers. Opt. Fiber Technol. 2018, 44, 13–23.
Tait, A.N.; De Lima, T.F.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Continuous Calibration of Microring Weights for Analog Optical Networks. IEEE Photonics Technol. Lett. 2016, 28, 887–890. Available online: https://ieeexplore.ieee.org/document/7377037 (accessed on 21 October 2023).
Tait, A.N.; De Lima, T.F.; Nahmias, M.A.; Miller, H.B.; Peng, H.T.; Shastri, B.J.; Prucnal, P.R. Silicon Photonic Modulator Neuron. Phys. Rev. Appl. 2019, 11, 064043. Available online: https://journals.aps.org/prapplied/abstract/10.1103/PhysRevApplied.11.064043 (accessed on 21 October 2023).
Tait, A.N.; de Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 7430.
de Lima, T.F.; Tait, A.N.; Mehrabian, A.; Nahmias, M.A.; Huang, C.; Peng, H.-T.; Marquez, B.A.; Miscuglio, M.; El-Ghazawi, T.; Sorger, V.J.; et al. Primer on silicon neuromorphic photonic processors: Architecture and compiler. Nanophotonics 2020, 9, 4055–4073.
Marquez, B.A.; Huang, C.; Prucnal, P.R.; Shastri, B.J. Neuromorphic Silicon Photonics for Artificial Intelligence. In Silicon Photonics IV: Innovative Frontiers; Lockwood, D.J., Pavesi, L., Eds.; Topics in Applied Physics; Springer International Publishing: Cham, Switzerland, 2021; pp. 417–447.
Xu, L.; de Lima, T.F.; Peng, H.-T.; Bilodeau, S.; Tait, A.; Shastri, B.J.; Prucnal, P.R. Scalable Networks of Neuromorphic Photonic Integrated Circuits. IIEEE J. Sel. Top. Quantum Electron. 2022, 28, 1–9.
Peng, S.; Zeng, R.; Liu, H.; Cao, L.; Wang, G.; Xie, J. Deep Broad Learning for Emotion Classification in Textual Conversations. Tsinghua Sci. Technol. 2024, 29, 481–491.
Taouktsis, X.; Zikopoulos, C. A decision-making tool for the determination of the distribution center location in a humanitarian logistics network. Expert Syst. Appl. 2024, 238, 122010.
Wu, H.; Lei, R.; Peng, Y.; Gao, L. AAGNet: A graph neural network towards multi-task machining feature recognition. Robot. Comput. Manuf. 2024, 86, 102661.
Choi, C.Q. 7 Revealing Ways AIs Fail: Neural Networks can be Disastrously Brittle, Forgetful, and Surprisingly Bad at Math. IEEE Spectr. 2021, 58, 42–47. Available online: https://ieeexplore.ieee.org/document/9563958 (accessed on 26 October 2023).
Searle, J.R. Minds, Brains, and Programs. Behav. Brain Sci. 1980, 3, 417–424. Available online: https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/minds-brains-and-programs/DC644B47A4299C637C89772FACC2706A (accessed on 26 October 2023).
Marcus, G. Deep Learning: A Critical Appraisal. arXiv 2018, arXiv:1801.00631.
Santoro, A.; Lampinen, A.; Mathewson, K.; Lillicrap, T.; Raposo, D. Symbolic Behaviour in Artificial Intelligence. arXiv 2022, arXiv:2102.03406.
Trask, A.; Hill, F.; Reed, S.E.; Rae, J.; Dyer, C.; Blunsom, P. Neural Arithmetic Logic Units. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Nice, France, 2018; Available online: https://proceedings.neurips.cc/paper_files/paper/2018/hash/0e64a7b00c83e3d22ce6b3acf2c582b6-Abstract.html (accessed on 26 October 2023).
Lample, G.; Charton, F. Deep Learning for Symbolic Mathematics. arXiv 2019, arXiv:1912.01412.
Lee, D.; Szegedy, C.; Rabe, M.N.; Loos, S.M.; Bansal, K. Mathematical Reasoning in Latent Space. arXiv 2019, arXiv:1909.11851.
Davies, A.; Veličković, P.; Buesing, L.; Blackwell, S.; Zheng, D.; Tomašev, N.; Tanburn, R.; Battaglia, P.; Blundell, C.; Juhász, A.; et al. Advancing Mathematics by Guiding Human Intuition with AI. Nature 2021, 600, 70–74. Available online: https://www.nature.com/articles/s41586-021-04086-x (accessed on 26 October 2023).
Fawzi, A.; Balog, M.; Huang, A.; Hubert, T.; Romera-Paredes, B.; Barekatain, M.; Novikov, A.; RRuiz, F.J.; Schrittwieser, J.; Swirszcz, G.; et al. Discovering Faster Matrix Multiplication Algorithms with Reinforcement Learning. Nature 2022, 610, 47–53. Available online: https://www.nature.com/articles/s41586-022-05172-4 (accessed on 26 October 2023).
Drori, I.; Zhang, S.; Shuttleworth, R.; Tang, L.; Lu, A.; Ke, E.; Liu, K.; Chen, L.; Tran, S.; Cheng, N.; et al. A Neural Network Solves, Explains, and Generates University Math Problems by Program Synthesis and Few-Shot Learning at Human Level. Proc. Natl. Acad. Sci. USA 2022, 119, e2123433119. Available online: https://www.pnas.org/doi/10.1073/pnas.2123433119 (accessed on 26 October 2023).
Jordan, N.C.; Kaplan, D.; Ramineni, C.; Locuniak, M.N. Early math matters: Kindergarten number competence and later mathematics outcomes. Dev. Psychol. 2009, 45, 850–867.
Liao, K.; Li, C.; Dai, T.; Zhong, C.; Lin, H.; Hu, X.; Gong, Q. Matrix eigenvalue solver based on reconfigurable photonic neural network. Nanophotonics 2022, 11, 4089–4099.
Wang, R.; Wang, P.; Lyu, C.; Luo, G.; Yu, H.; Zhou, X.; Zhang, Y.; Pan, J. Multicore Photonic Complex-Valued Neural Network with Transformation Layer. Photonics 2022, 9, 384.
Zhang, H.; Gu, M.; Jiang, X.D.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457.
Cheng, J.; Zhao, Y.; Zhang, W.; Zhou, H.; Huang, D.; Zhu, Q.; Guo, Y.; Xu, B.; Dong, J.; Zhang, X. A small microring array that performs large complex-valued matrix-vector multiplication. Front. Optoelectron. 2022, 15, 15.
Goel, A.; Goel, A.K.; Kumar, A. The Role of Artificial Neural Network and Machine Learning in Utilizing Spatial Information. Spat. Inf. Res. 2023, 31, 275–285. Available online: https://link.springer.com/article/10.1007/s41324-022-00494-x (accessed on 25 October 2023).
Yamazaki, K.; Vo-Ho, V.-K.; Bulsara, D.; Le, N. Spiking Neural Networks and Their Applications: A Review. Brain Sci. 2022, 12, 863.
Zhang, D.; Yang, J.; Ye, D.; Hua, G. LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 365–382. Available online: https://openaccess.thecvf.com/content_ECCV_2018/html/Dongqing_Zhang_Optimized_Quantization_for_ECCV_2018_paper.html (accessed on 25 October 2023).
Li, G.; Qian, C.; Jiang, C.; Lu, X.; Tang, K. Optimization based Layer-wise Magnitude-based Pruning for DNN Compression. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13 July 2018; International Joint Conferences on Artificial Intelligence Organization: San Francisco, CA, USA, 2018; pp. 2383–2389.
Jin, X.; Peng, B.; Wu, Y.; Liu, Y.; Liu, J.; Liang, D.; Yan, J.; Hu, X. Knowledge Distillation via Route Constrained Optimization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, October 27–November 2 2019; pp. 1345–1354. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Jin_Knowledge_Distillation_via_Route_Constrained_Optimization_ICCV_2019_paper.html (accessed on 25 October 2023).
Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673.
Davies, M.; Srinivasa, N.; Lin, T.-H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99.
Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665.
Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.-M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716.
Kasabov, N.K. Time-Space, Spiking Neural Networks and Brain-Inspired Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; Available online: https://link.springer.com/book/10.1007/978-3-662-57715-8 (accessed on 25 October 2023).
Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574–591.
Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154.2.
Mo, W.; Luo, X.; Zhong, Y.; Jiang, W. Image recognition using convolutional neural network combined with ensemble learning algorithm. J. Phys. Conf. Ser. 2019, 1237, 022026.
Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. Available online: https://pubmed.ncbi.nlm.nih.gov/28599112/ (accessed on 25 October 2023).
He, Y.; Zhao, C.; Zhou, X.; Shen, W. MJAR: A novel joint generalization-based diagnosis method for industrial robots with compound faults. Robot. Comput. Manuf. 2024, 86, 102668.
Daidone, M.; Ferrantelli, S.; Tuttolomondo, A. Machine learning applications in stroke medicine: Advancements, challenges, and future prospectives. Neural Regen. Res. 2024, 19, 769–773.
Pacal, I. Enhancing crop productivity and sustainability through disease identification in maize leaves: Exploiting a large dataset with an advanced vision transformer model. Expert Syst. Appl. 2024, 238, 122099.
Stoica, I.; Song, D.; Popa, R.A.; Patterson, D.; Mahoney, M.W.; Katz, R.; Joseph, A.D.; Jordan, M.; Hellerstein, J.M.; Gonzalez, J.E.; et al. A Berkeley View of Systems Challenges for AI. arXiv 2017, arXiv:1712.05855. Available online: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2017/EECS-2017-159.html (accessed on 24 October 2023).
Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An Energy-Efficient Reconfigurable Accelerator for Deep Convolutional Neural Networks. IEEE J. Mag. 2016, 52, 127–138. Available online: https://ieeexplore.ieee.org/document/7738524 (accessed on 24 October 2023).
De Lima, T.F.; Peng, H.T.; Tait, A.N.; Nahmias, M.A.; Miller, H.B.; Shastri, B.J.; Prucnal, P.R. Machine Learning with Neuromorphic Photonics. IEEE J. Mag. 2019, 37, 1515–1534. Available online: https://ieeexplore.ieee.org/document/8662590 (accessed on 21 October 2023).
Bai, B.; Shu, H.; Wang, X.; Zou, W. Towards Silicon Photonic Neural Networks for Artificial Intelligence. Sci. China Inf. Sci. 2020, 63, 1–14. Available online: https://link.springer.com/article/10.1007/s11432-020-2872-3 (accessed on 24 October 2023).
Sacher, W.D.; Poon, J.K. Dynamics of Microring Resonator Modulators. Opt. Express 2008, 16, 15741–15753. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-16-20-15741&id=172148 (accessed on 24 October 2023).
Hassanien, A.E.; Ghoname, A.O.; Chow, E.; Goddard, L.L.; Gong, S. Compact MZI Modulators on Thin Film Z-Cut Lithium Niobate. Opt. Express 2022, 30, 4543–4552. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-30-3-4543&id=468841 (accessed on 24 October 2023).
Hughes, T.W.; Minkov, M.; Shi, Y.; Fan, S. Training of Photonic Neural Networks through in Situ Backpropagation and Gradient Measurement. Optica 2018, 5, 864–871. Available online: https://opg.optica.org/optica/fulltext.cfm?uri=optica-5-7-864&id=395466 (accessed on 24 October 2023).
Wu, B.; Li, H.; Tong, W.; Dong, J.; Zhang, X. Low-threshold all-optical nonlinear activation function based on a Ge/Si hybrid structure in a microring resonator. Opt. Mater. Express 2022, 12, 970–980.
Jha, A.; Huang, C.; Prucnal, P.R. Reconfigurable all-optical nonlinear activation functions for neuromorphic photonics. Opt. Lett. 2020, 45, 4819–4822.
Tait, A.N.; Shastri, B.J.; Fok, M.P.; Nahmias, M.A.; Prucnal, P.R. The DREAM: An Integrated Photonic Thresholder. J. Light. Technol. 2013, 31, 1263–1272.
Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214.
Xu, Z.; Tang, B.; Zhang, X.; Leong, J.F.; Pan, J.; Hooda, S.; Zamburg, E.; Thean, A.V.-Y. Reconfigurable nonlinear photonic activation function for photonic neural network based on non-volatile opto-resistive RAM switch. Light. Sci. Appl. 2022, 11, 288.
Hamerly, R.; Bernstein, L.; Sludds, A.; Soljačić, M.; Englund, D. Large-Scale Optical Neural Networks Based on Photoelectric Multiplication. Phys. Rev. X 2019, 9, 021032. Available online: https://journals.aps.org/prx/abstract/10.1103/PhysRevX.9.021032 (accessed on 24 October 2023).
Sludds, A.; Bandyopadhyay, S.; Chen, Z.; Zhong, Z.; Cochrane, J.; Bernstein, L.; Bunandar, D.; Dixon, P.B.; Hamilton, S.A.; Streshinsky, M.; et al. Delocalized Photonic Deep Learning on the Internet’s Edge. Science 2022, 378, 270–276. Available online: https://www.science.org/doi/10.1126/science.abq8271 (accessed on 24 October 2023).
Zuo, Y.; Li, B.; Zhao, Y.; Jiang, Y.; Chen, Y.-C.; Chen, P.; Jo, G.-B.; Liu, J.; Du, S. All-optical neural network with nonlinear activation functions. Optica 2019, 6, 1132–1137.
Bonifacio, R.; Lugiato, L.A.; Gronchi, M. Theory of Optical Bistability; Springer: Berlin/Heidelberg, Germany, 1979; Available online: https://link.springer.com/chapter/10.1007/978-3-540-38950-7_45 (accessed on 24 October 2023).
Zhang, P.; Chung, T.F.; Li, Q.; Wang, S.; Wang, Q.; Huey, W.L.; Yang, S.; Goldberger, J.E.; Yao, J.; Zhang, X. All-Optical Switching of Magnetization in Atomically Thin CrI3. Nat. Mater. 2022, 21, 1373–1378. Available online: https://www.nature.com/articles/s41563-022-01354-7 (accessed on 24 October 2023).
Li, Q.; Liu, S.; Zhao, Y.; Wang, W.; Tian, Y.; Feng, J.; Guo, J. Optical Nonlinear Activation Functions Based on MZI-Structure for Optical Neural Networks. In Proceedings of the 2020 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 24–27 October 2020; Available online: https://ieeexplore.ieee.org/document/9365615 (accessed on 24 October 2023).
Lin, Q.; Ma, J.; Yin, Z.; Yuan, P.; Wang, J.; Xie, G.; Qian, L. Optical modification of nonlinear crystals for quasi-parametric chirped-pulse amplification. Fundam. Res. 2022.
All Optical Nonlinear Activation Function Based on Ge/Si Hybrid Micro-Ring Resonator. Available online: https://opg.optica.org/abstract.cfm?uri=ACPC-2021-M5I.6 (accessed on 24 October 2023).
Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel Convolutional Processing Using an Integrated Photonic Tensor Core. Nature 2021, 598, 52–58. Available online: https://www.nature.com/articles/s41586-020-03070-1 (accessed on 24 October 2023).
Porte, X.; Skalli, A.; Haghighi, N.; Reitzenstein, S.; Lott, J.A.; Brunner, D. A Complete, Parallel and Autonomous Photonic Neural Network in a Semiconductor Multimode Laser. J. Phys. Photonics 2021, 3, 024017. Available online: https://iopscience.iop.org/article/10.1088/2515-7647/abf6bd (accessed on 24 October 2023).
Totovic, A.R.; Dabos, G.; Passalis, N.; Tefas, A.; Pleros, N. Femtojoule per MAC Neuromorphic Photonics: An Energy and Technology Roadmap. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–15.
Nahmias, M.A.; de Lima, T.F.; Tait, A.N.; Peng, H.-T.; Shastri, B.J.; Prucnal, P.R. Photonic Multiply-Accumulate Operations for Neural Networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–18.
Pai, S.; Williamson, I.A.; Hughes, T.W.; Minkov, M.; Solgaard, O.; Fan, S.; Miller, D.A. Parallel Programming of an Arbitrary Feedforward Photonic Network. IEEE J. Mag. 2020, 26, 6100813. Available online: https://ieeexplore.ieee.org/document/9103211 (accessed on 24 October 2023).
Lu, T.; Wu, S.; Xu, X.; Yu, F.T.S. Two-dimensional programmable optical neural network. Appl. Opt. 1989, 28, 4908–4913.
Huang, C.; Jha, A.; De Lima, T.F.; Tait, A.N.; Shastri, B.J.; Prucnal, P.R. On-Chip Programmable Nonlinear Optical Signal Processor and Its Applications. IEEE J. Mag. 2020, 27, 6100211. Available online: https://ieeexplore.ieee.org/document/9104002 (accessed on 24 October 2023).
Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS Photonic Convolutional Accelerator for Optical Neural Networks. Nature 2021, 598, 44–51. Available online: https://www.nature.com/articles/s41586-020-03063-0 (accessed on 24 October 2023).
Totovic, A.; Giamougiannis, G.; Tsakyridis, A.; Lazovsky, D.; Pleros, N. Programmable photonic neural networks combining WDM with coherent linear optics. Sci. Rep. 2022, 12, 5605.
Mourgias-Alexandris, G.; Totovic, A.; Tsakyridis, A.; Passalis, N.; Vyrsokinos, K.; Tefas, A.; Pleros, N. Neuromorphic Photonics With Coherent Linear Neurons Using Dual-IQ Modulation Cells. J. Light. Technol. 2020, 38, 811–819.
Giamougiannis, G.; Tsakyridis, A.; Mourgias-Alexandris, G.; Moralis-Pegios, M.; Totovic, A.; Dabos, G.; Passalis, N.; Kirtas, M.; Bamiedakis, N.; Tefas, A.; et al. Silicon-integrated coherent neurons with 32GMAC/sec/axon compute line-rates using EAM-based input and weighting cells. In Proceedings of the 2021 European Conference on Optical Communication (ECOC), Bordeaux, France, 13–16 September 2021; IEEE: Piscataway Township, NJ, USA, 2021; pp. 1–4.
Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61.
Optimal Design for Universal Multiport Interferometers. Available online: https://opg.optica.org/optica/fulltext.cfm?uri=optica-3-12-1460&id=355743 (accessed on 24 October 2023).
Fard, M.M.P.; Williamson, I.A.; Edwards, M.; Liu, K.; Pai, S.; Bartlett, B.; Minkov, M.; Hughes, T.W.; Fan, S.; Nguyen, T.A. Experimental Realization of Arbitrary Activation Functions for Optical Neural Networks. Opt. Express 2020, 28, 12138–12148. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-28-8-12138&id=429881 (accessed on 24 October 2023).
Liang, G.; Huang, H.; Mohanty, A.; Shin, M.C.; Ji, X.; Carter, M.J.; Shrestha, S.; Lipson, M.; Yu, N. Robust, Efficient, Micrometre-Scale Phase Modulators at Visible Wavelengths. Nat. Photonics 2021, 15, 908–913. Available online: https://www.nature.com/articles/s41566-021-00891-y (accessed on 24 October 2023).
Tait, A.N.; Wu, A.X.; De Lima, T.F.; Zhou, E.; Shastri, B.J.; Nahmias, M.A.; Prucnal, P.R. Microring Weight Banks. IEEE J. Mag. 2016, 22, 312–325. Available online: https://ieeexplore.ieee.org/document/7479545/ (accessed on 24 October 2023).
Miscuglio, M.; Sorger, V.J. Photonic Tensor Cores for Machine Learning. Appl. Phys. Rev. 2020, 7, 031404. Available online: https://pubs.aip.org/aip/apr/article/7/3/031404/998338/Photonic-tensor-cores-for-machine-learning (accessed on 24 October 2023).
Wang, J.; Rodrigues, S.P.; Dede, E.M.; Fan, S. Microring-based programmable coherent optical neural networks. Opt. Express 2023, 31, 18871.
Sato, T.; Enokihara, A. Ultrasmall design of a universal linear circuit based on microring resonators. Opt. Express 2019, 27, 33005–33010.
Deng, L. The MNIST Database of Handwritten Digit Images for Machine Learning Research . IEEE J. Mag. 2012, 18, 141–142. Available online: https://ieeexplore.ieee.org/document/6296535 (accessed on 24 October 2023).

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Optics

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ruslan V. Kutluyarov

Aida G. Zakoyan

Grigory S. Voronkov

Elizaveta P. Grakhova

Muhammad A. Butt

View Times: 96

Update Date: 10 Jan 2024

Table of Contents

Video Upload Options

Confirm