Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Ying Wang
 -- 1532 2024-01-03 07:21:14 |
2 format
Jason Zhu
 Meta information modification 1532 2024-01-08 06:56:26 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Wang, Y.; Chen, Y.; Yao, Y.; Ou, J. Engineering Applications of Optimal Sensor Placement for SHM. Encyclopedia. Available online: https://encyclopedia.pub/entry/53352 (accessed on 17 November 2024).
Wang Y, Chen Y, Yao Y, Ou J. Engineering Applications of Optimal Sensor Placement for SHM. Encyclopedia. Available at: https://encyclopedia.pub/entry/53352. Accessed November 17, 2024.
Wang, Ying, Yue Chen, Yuhan Yao, Jinping Ou. "Engineering Applications of Optimal Sensor Placement for SHM" Encyclopedia, https://encyclopedia.pub/entry/53352 (accessed November 17, 2024).
Wang, Y., Chen, Y., Yao, Y., & Ou, J. (2024, January 03). Engineering Applications of Optimal Sensor Placement for SHM. In Encyclopedia. https://encyclopedia.pub/entry/53352
Wang, Ying, et al. "Engineering Applications of Optimal Sensor Placement for SHM." Encyclopedia. Web. 03 January, 2024.
Engineering Applications of Optimal Sensor Placement for SHM
Edit
This entry is adapted from the peer-reviewed paper 10.3390/buildings13123129

Structural health monitoring (SHM) is critical to maintaining safe and reliable civil infrastructure, but the optimal design of an SHM sensing system, i.e., optimal sensor placement (OSP), remains a complex challenge.

structural health monitoring (SHM) optimal sensor placement (OSP)

1. Bridges

Several studies have explored OSP for monitoring bridges in different locations. These studies utilize various techniques such as the effective independence approach, ant colony algorithm, MAC, and other optimization algorithms. Researchers have applied these methodologies to bridges in Poland, Spain, Dalian, Italy, Liaoning, Harbin, and Foshan, demonstrating the versatility and effectiveness of sensor placement for structural monitoring.
Figure 1 depicts the strategic arrangement of accelerometers on the Yingwuzhou Yangtze River Bridge, a three-tower, four-span suspension bridge, which extends 3.42 km in length, with its main span reaching 850 m, connecting Hanyang and Wuchang. It is equipped with an array of 58 sensors, including thermometers, anemometers, and accelerometers. These sensors facilitate real-time tracking of the bridge’s condition, ensuring its safety and operational integrity.
Buildings 13 03129 g011
Figure 1. Layout of Yingwuzhou Yangtze River Bridge. (a) The real bridge overview, (b) layout of monitoring sensors of the bridge [1].
Moreover, Błachowski et al. [2] undertook OSP for load monitoring using the effective independence method, augmented by convex relaxation, on a tied-arch simply supported bridge situated in Poland. Pachón et al. [3] utilized the effective independence method to determine optimal sensor locations for the E. Torroja bridge, constructed in Spain in 1957. In a study by Feng et al. [4], an optimal arrangement method for triaxial sensors, complemented by the effective independence approach, was employed to assess the Dalian South Bay Cross-sea Bridge. Furthermore, Vincenzi et al. [5] introduced a novel methodology based on IE theory, integrating both distance and modal vectors, for OSP on a pedestrian bridge in Italy. These practical applications showcase the versatility and effectiveness of sensor placement methodologies across diverse structural scenarios.
Meanwhile, Feng et al. [6] introduced an arrangement method for triaxial acceleration sensors, leveraging the ant colony algorithm and MAC, and implemented this approach on the North Bridge in Dalian, Liaoning. Yang et al. [7] proposed a beetle-swarm evolution competitive algorithm with MAC as the objective function, effectively applied to a large-span bridge on the Haqi high-speed railroad in Harbin. Luo et al. [8] developed a novel harmony search cat swarm optimization algorithm, utilizing the MAC matrix’s non-diagonal element maxima as the evaluation criterion, which was successfully employed for the Beijiang Bridge in Foshan, Guangdong. Zhou et al. [9] innovatively merged the MAC evaluation criterion with considerations of wireless sensor connectivity and energy balance to formulate a hybrid discrete firefly algorithm, deployed on the Runyang Yangtze River Highway Bridge in Jiangsu Province.
Moreover, Xiao et al. [10] focuses on identifying damage in large-scale space truss structures using a stiffness separation method, particularly aimed at large-scale structures where traditional damage detection methods may be less effective due to the complexity and size of the structures. Later, by using numerical optimization, Xiao’s team determined the minimal number of sensors and their most effective layout for evaluating a bridge’s structural condition [11].

2. High-Rise Buildings

High-rise buildings, both current and future, have a significant need for SHM. In this part, studies have utilized different evaluation criteria such as MAC, MKE, and a combination of both. Researchers have conducted trials on diverse structures, including MIT campus buildings, the Canton Tower, Shanghai Center Tower, Shanghai Center Building, Jingji Financial Center, Dalian World Trade Center, and the Civil Engineering Research Building of National Taiwan University. The outcomes of these studies showcase the effectiveness and advantages of these innovative algorithms in achieving OSP for monitoring high-rise buildings and superstructures.
The Canton Tower in South China, standing at 610 m, is equipped with a long-term SHM system featuring over 700 sensors of 16 types. Ni et al. [12] developed a reduced-order FEM for benchmarking, comprising 37 beam elements and 185 DOFs, closely matching the full-scale FEM in modal frequencies and shapes. This benchmark study includes field data from 20 accelerometers, an anemometer, and a temperature sensor, along with details on sensor locations and specifications, as shown in Figure 2.
Buildings 13 03129 g012
Figure 2. Benchmark model of Canton Tower [13].
Additionally, Sun et al. [14] proposed a discrete optimization scheme based on an artificial bee colony algorithm, using MAC as the evaluation criterion, and conducted trials on various structures, including campus buildings at MIT and the iconic Canton Tower. Mahjoubi et al. [15] introduced a hypotrochoid spiral optimization algorithm to study optimal triaxial accelerometer placement for high-rise building monitoring. In an extensive evaluation using seven optimization algorithms, the efficiency of these approaches was assessed using the 632-m Shanghai Center Tower as a case study, with MAC as the key evaluation criterion. To realize the reconstruction of response to ground shaking, Hu et al. [16] applied a sequential sensor placement algorithm to achieve the OSP configuration with the minimum reconstruction error, and illustrated it with the example of Shanghai Center Building. By using the Jingji Financial Center as the engineering background, Fan et al. [17] studied the super high-rise construction monitoring system, applying the whole process of construction simulation technology to the OSP, according to the structural response changes in the process of construction simulation, to design a suitable temperature, vertical displacement, and stress measurement points placement scheme. Yi et al. [18] improved the monkey swarm algorithm and combined it with the MAC objective function to apply it in the Dalian World Trade Center, illustrating the advantages of the algorithm. Yang et al. [19] proposed an OSP method that can be used for structures that require repetitive monitoring to reduce the number of sensors required and to find the higher modal frequencies of the structure and illustrated the workability of the method by conducting a field test at the Civil Engineering Research Building of National Taiwan University. Mghazli et al. [20] combined the objective functions of MKE and MAC in a mixed meta-heuristic algorithm to design an OSP for the Willis Tower in Chicago and compared it with other algorithms to illustrate the effectiveness of the algorithm.

3. Others

Structures with complex designs, such as stadiums and museums, require SHM due to their architectural intricacies and high usage. SHM is essential for early detection of structural issues, ensuring safety, and preserving the integrity of these culturally significant buildings. This proactive approach is crucial for their long-term durability and safe operation.
The Shenzhen Sports Center spans 57,500 square meters and features a grandstand capable of seating approximately 45,000 spectators. The stadium is characterized by its elliptical grandstand, which measures 258 m along its major axis and 200 m along its minor axis, with the field’s main axis oriented north–south. The structure’s highest point reaches 32 m, featuring a grandstand that includes both upper and lower seating sections and a layer of private boxes sandwiched in between. The stadium is equipped with an SHM system that includes more than 100 sensors of four different types, strategically placed to monitor various critical points throughout the stadium, as shown in Figure 3.
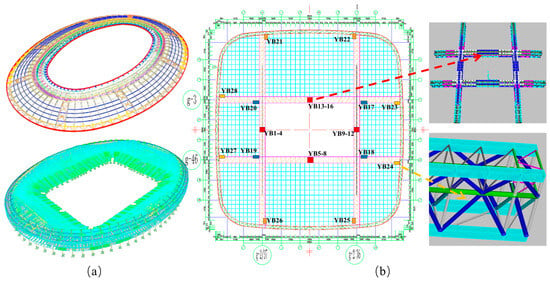
Buildings 13 03129 g013
Figure 3. Sensors placement for Shenzhen Sports Center. (a) Overview of the Center, up: steel roof, down: grandstand, (b) locations of strain gauges.
Teng et al. [21] proposed a GA based on modal energy for optimal placement of multi-objective sensors and used the steel structure of the National Swimming Center as an engineering background to optimize the placement of acceleration sensors during its modal testing process. Xu et al. [22] used the particle swarm algorithm to optimize the arrangement of acceleration sensors and strain sensors in the monitoring system of Xining City Stadium, respectively. Jin et al. [23] used the effective independence method for OSP on the giant telescope cable network structure.
Wang et al. [24] proposed a new method named “Reduced Redundant Biaxial Modal Assurance Criteria” based on the three-dimensional modal assurance criterion for optimal placement of biaxial acceleration sensors and illustrated the advantages of the RRBMAC method with the example of a lattice transmission tower. Based on the ant colony optimization (ACO) algorithm, Feng et al. [25] proposed the “siege ant colony algorithm”, which aims to improve the efficiency and accuracy of the OSP problem in large-scale structure monitoring. The method is applied and compared with the standard method by using the Han River transmission tower as an example.
Schulze et al. [26] used a GA to minimize MAC non-diagonal elements to design an optimal solution for acceleration sensors for a 3-MWwind turbine. Cong et al. [27] developed a comprehensive strategy involving OSP, complex mode expansion, and cross-model cross-mode-based model updating technique. To demonstrate the effectiveness of the proposed method, computer simulations with the National Renewable Energy Laboratory 5-MW reference turbine are carried out.
Yan et al. [28] studied the method of OSP for offshore platforms using the example of an offshore platform in the South China Sea. Wang et al. [29] proposed an offshore platform sensor position fractional order optimization method and applied the effective independence method to experimentally study the fractional order placement of the sensors and validated the method with an offshore platform in Jinzhou as an example. A digital twin framework with OSP to accurately calculate the modal response and identify the damage rate of an offshore jacket platform was proposed by Wang et al. [30]. The OSP model was validated using a multi-objective Lichtenberg’s algorithm for sensor number/location optimization, and the proposed method was validated using an offshore jacket platform. These applications underscore the diverse range of innovative OSP for SHM.

References

  1. Hou, J.L.; Cao, S.G.; Hu, H.; Zhou, Z.W.; Wan, C.F.; Noori, M.; Li, P.Y.; Luo, Y.A. Vortex-Induced Vibration Recognition for Long-Span Bridges Based on Transfer Component Analysis. Buildings 2023, 13, 2012.
  2. Blachowski, B.; Swiercz, A.; Ostrowski, M.; Tauzowski, P.; Olaszek, P.; Jankowski, L. Convex relaxation for efficient sensor layout optimization in large-scale structures subjected to moving loads. Comput. Aided Civ. Infrastruct. Eng. 2020, 35, 1085–1100.
  3. Pachon, P.; Castro, R.; Garcia-Macias, E.; Compan, V.; Puertas, E.E. Torroja’s bridge: Tailored experimental setup for SHM of a historical bridge with a reduced number of sensors. Eng. Struct. 2018, 162, 11–21.
  4. Feng, S.; Jia, J.Q. Acceleration sensor placement technique for vibration test in structural health monitoring using microhabitat frog-leaping algorithm. Struct. Health Monit. 2018, 17, 169–184.
  5. Vincenzi, L.; Simonini, L. Influence of model errors in optimal sensor placement. J. Sound. Vib. 2017, 389, 119–133.
  6. Feng, S.; Jia, J.Q. 3D sensor placement strategy using the full-range pheromone ant colony system. Smart Mater. Struct. 2016, 25, 075003.
  7. Yang, J.H.; Peng, Z.R. Beetle-Swarm Evolution Competitive Algorithm for Bridge Sensor Optimal Placement in SHM. IEEE Sens. J. 2020, 20, 8244–8255.
  8. Luo, B.; Yi, L.; Wu, H.; Qiu, Y.; Li, X.; Tang, F.; Zhang, Y. A Novel Harmony Search Cat Swarm Optimization Algorithm for Optimal Bridge Sensor Placement. In Proceedings of the 2022 IEEE International Conferences on Internet of Things (iThings) and IEEE Green Computing & Communications (GreenCom) and IEEE Cyber, Physical & Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Espoo, Finland, 22–25 August 2022; pp. 41–47.
  9. Zhou, G.D.; Yi, T.H.; Zhang, H.; Li, H.N. Energy-aware wireless sensor placement in structural health monitoring using hybrid discrete firefly algorithm. Struct. Control. Health Monit. 2015, 22, 648–666.
  10. Xiao, F.; Sun, H.M.; Mao, Y.X.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118.
  11. Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y.J. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13, 11.
  12. Ni, Y.Q.; Xia, Y.; Lin, W.; Chen, W.H.; Ko, J.M. SHM benchmark for high-rise structures: A reduced-order finite element model and field measurement data. Smart. Struct. Syst. 2012, 10, 411–426.
  13. Lin, W.; Song, G.B.; Chen, S.H. PTMD Control on a Benchmark TV Tower under Earthquake and Wind Load Excitations. Appl. Sci. 2017, 7, 425.
  14. Sun, H.; Buyukozturk, O. Optimal sensor placement in structural health monitoring using discrete optimization. Smart Mater. Struct. 2015, 24, 125034.
  15. Mahjoubi, S.; Barhemat, R.; Bao, Y. Optimal placement of triaxial accelerometers using hypotrochoid spiral optimization algorithm for automated monitoring of high-rise buildings. Autom. Constr. 2020, 118, 103273.
  16. Hu, R.P.; Xu, Y.L.; Zhao, X. Optimal multi-type sensor placement for monitoring high-rise buildings under bidirectional long-period ground motions. Struct. Control. Health Monit. 2020, 27, e2541.
  17. Feng, F.A.N.; Huajie, W.; Xiaofei, J.I.N.; Xudong, Z.H.I.; Gang, H.; Jianxin, L.U.; Enchun, Z.H.U. Development and application of construction monitoring system for super high-rise buildings. J. Build. Struct. 2011, 32, 50–59.
  18. Yi, T.H.; Li, H.N.; Song, G.B.; Zhang, X.D. Optimal sensor placement for health monitoring of high-rise structure using adaptive monkey algorithm. Struct. Control. Health Monit. 2015, 22, 667–681.
  19. Yang, Y.Y.; Leu, L.J. Optimal sensors placement for structural health monitoring based on system identification and interpolation methods. J. Chin. Inst. Eng. 2021, 44, 803–819.
  20. Mghazli, M.O.; Zoubir, Z.; Nait-Taour, A.; Cherif, S.; Lamdouar, N.; El Mankibi, M. Optimal sensor placement methodology of triaxial accelerometers using combined metaheuristic algorithms for structural health monitoring applications. Structures 2023, 51, 1959–1971.
  21. Teng, J.; Zhu, Y. Optimal sensor placement for modal parameters test of large span spatial steel structural. Eng. Mech. 2011, 28, 150–156.
  22. Xu, J.; Liu, B.; Dong, J.; Zhang, C.; Wang, X. Optimal placement of sensors for monitoring systems on agymnasium using particle swarm optimization. Spat. Struct. 2019, 25, 40–46.
  23. Jin, X.-f.; Fan, F.; Qian, H.-l.; Shen, S.-z. Optimal sensor placement of 30-meter scaled structure of large telescope FAST. J. Harbin Inst. Technol. 2009, 41, 31–35.
  24. Wang, Z.; Wang, J. Optimal placement of biaxial acceleration sensor for transmission towers. Chin. J. Sci. Instrum. 2017, 38, 2200–2209.
  25. Feng, S.; Jia, J.Q.; Zhang, J.C. Sensor configuration optimizing in modal identification by siege ant colony algorithm. J. Mech. 2017, 33, 269–277.
  26. Schulze, A.; Zierath, J.; Rosenow, S.E.; Bockhahn, R.; Rachholz, R.; Woernle, C. Optimal sensor placement for modal testing on wind turbines. In Proceedings of the Conference on Science of Making Torque from Wind (TORQUE), Munich, Germany, 5–7 October 2016.
  27. Cong, S.; Hu, S.L.J.; Li, H.J. Using incomplete complex modes for model updating of monopiled offshore wind turbines. Renew. Energy 2022, 181, 522–534.
  28. Yan, T.; Zhou, G.; Wang, W.; Zhao, H. Optimal sensor placement of structural health monitoring for jacket platform. J. Mach. Des. 2022, 39, 51–55.
  29. Wang, C.; Liu, F.; Li, W. Experiment Study of Optimal Sensor Placement on Offshore Platform for Different Mode Orders. J. Ocean. Univ. China 2013, 43, 103–108.
  30. Wang, M.M.; Incecik, A.; Feng, S.Z.; Gupta, M.K.; Królczyk, G.; Li, Z. Damage identification of offshore jacket platforms in a digital twin framework considering optimal sensor placement. Reliab. Eng. Syst. Saf. 2023, 237, 109336.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Civil
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Ying Wang
,
Yue Chen
,
Yuhan Yao
,
Jinping Ou
View Times: 259
Revisions: 2 times (View History)
Update Date: 08 Jan 2024
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback