Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Philipp Glira | -- | 1566 | 2023-11-23 09:11:37 | | | |
| 2 | Sirius Huang | Meta information modification | 1566 | 2023-11-24 02:00:41 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Glira, P.; Weidinger, C.; Otepka-Schremmer, J.; Ressl, C.; Pfeifer, N.; Haberler-Weber, M. Variants of Point Cloud Registration Algorithms. Encyclopedia. Available online: https://encyclopedia.pub/entry/51978 (accessed on 07 February 2026).
Glira P, Weidinger C, Otepka-Schremmer J, Ressl C, Pfeifer N, Haberler-Weber M. Variants of Point Cloud Registration Algorithms. Encyclopedia. Available at: https://encyclopedia.pub/entry/51978. Accessed February 07, 2026.
Glira, Philipp, Christoph Weidinger, Johannes Otepka-Schremmer, Camillo Ressl, Norbert Pfeifer, Michaela Haberler-Weber. "Variants of Point Cloud Registration Algorithms" Encyclopedia, https://encyclopedia.pub/entry/51978 (accessed February 07, 2026).
Glira, P., Weidinger, C., Otepka-Schremmer, J., Ressl, C., Pfeifer, N., & Haberler-Weber, M. (2023, November 23). Variants of Point Cloud Registration Algorithms. In Encyclopedia. https://encyclopedia.pub/entry/51978
Glira, Philipp, et al. "Variants of Point Cloud Registration Algorithms." Encyclopedia. Web. 23 November, 2023.
Copy Citation
The registration of point clouds is relevant in many application domains, e.g., remote sensing, computer vision, robotics, autonomous driving, or healthcare. The general objective is to minimize the distances between overlapping point clouds.
point cloud registration
iterative closest point
transformation
lidar
1. Introduction
The registration of point clouds, i.e., a set of 2D or 3D points in object space, is relevant in many application domains, e.g., remote sensing, computer vision, robotics, autonomous driving, or healthcare. The general objective is to minimize the distances between overlapping point clouds. To achieve this, some kind of geometric transformation 𝒯 is estimated and applied individually to each nonfixed point cloud. The transformed point clouds can be regarded as optimally registered if the residual distances are purely random, i.e., if they are nonsystematic. In case a rigid-body transformation is not sufficient to model the discrepancies between the point clouds, a nonrigid transformation is needed—an example is shown in Figure 1.
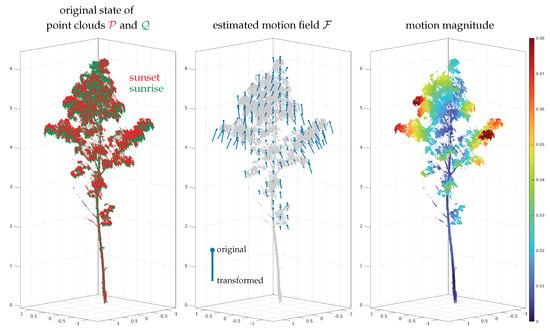
Figure 1. Example for a nonrigid registration between two point clouds.
Most point cloud registration methods are inspired indubitably by the works of Besl and McKay [1] and Chen and Medioni [2], who introduced approximately at the same time the iterative closest point (ICP) algorithm. It is used to improve the alignment of two point clouds by minimizing iteratively the distances within the overlap area of these point clouds. Nowadays, the term ICP does not necessarily refer to the algorithm presented in these original publications, but rather to a group of point cloud registration algorithms that have in common the following aspects: (I) correspondences are established iteratively; (C) the closest point, or more generally, the corresponding point, is used as correspondence; and (P) correspondences are established on a point basis [3].
A general taxonomy for ICP-based algorithms was introduced by Rusinkiewicz and Levoy [4]. Accordingly, a traditional point cloud registration pipeline can be roughly divided into five stages, cf. Figure 2. For the registration of a fixed point cloud 𝒬 and a loose point cloud 𝒫, these stages are:
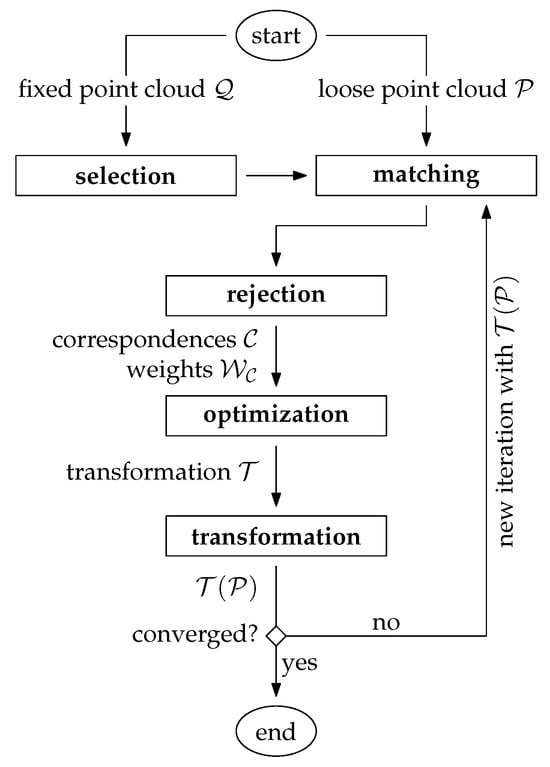
Figure 2. ICP-based point cloud registration pipeline.
-
Selection: A subset of points (instead of using each point) is selected within the overlap area in one point cloud [3]. For this, the fixed point cloud 𝒬 is typically chosen.
-
Matching: The points, which correspond to the selected subset, are determined in the other point cloud, typically the loose point cloud 𝒫.
-
Rejection: False correspondences (outliers) are rejected on the basis of the compatibility of points. The result of these first three stages is a set of correspondences 𝒞 with an associated set of weights 𝒲𝒞.
-
Optimization: The transformation 𝒯 for the loose point cloud is estimated by minimizing the weighted and squared distances (e.g., the Euclidean distances) between corresponding points.
-
Transformation: The estimated transformation 𝒯 is applied to the loose point cloud: 𝒯(𝒫).
Finally, a suitable convergence criterion is tested. If it is not met, a new iteration restarts from the matching stage using the transformed loose point cloud 𝒯(𝒫). The iterative nature of the ICP algorithm results from the following basic assumption: in the first iteration, correspondences are often imperfect due to a typically relatively large displacement of the two point clouds. With each transformation of the loose point cloud 𝒫, however, the correspondence assignments get better. Thus, this process is repeated until the correspondences become stable, i.e., until the variations become statistically insignificant. In this case, convergence is assumed to be achieved and the algorithm ends.
2. Variants of Point Cloud Registration Algorithms
For each of the five stages, multiple variations have been proposed in the past for many different applications—literature surveys can be found in [5][6][7][8]. As a brief review, point cloud registration algorithms can be roughly classified according to the following properties
-
Coarse registration vs. fine registration: Often the initial relative orientation of the point clouds is unknown in advance, e.g., if an object or a scene is scanned from multiple arbitrary view points. The problem of finding an initial transformation between the point clouds in the global parameter space is often denoted as coarse registration. Solutions to this problem are typically heavily based on matching of orientation-invariant point descriptors [9]. The 3DMatch benchmark introduced by [10] evaluates the performance of 2D and 3D descriptors for the coarse registration problem. Once a coarse registration of the point clouds is found that lies in the convergence basin of the global minima, a local optimization, typically some variant of the ICP algorithm, can be applied for the fine registration. It is noted that in case of multisensor setups, the coarse registration is often observed by means of other sensor modalities. For instance, in case of dynamic laser scanning systems, e.g., airborne laser scanning (ALS) or mobile laser scanning (MLS), the coarse registration between overlapping point clouds is directly given through the GNSS/IMU trajectory of the platform—in such cases, only a refinement of the point cloud registration is needed, e.g., by strip adjustment or (visual-)lidar SLAM (see below).
-
Rigid transformation vs. nonrigid transformation: Rigid methods apply a rigid-body transformation to one of the two point clouds to improve their relative alignment. A rigid-body transformation has 3/6 degrees of freedom (DoF) in 2D/3D and is usually parameterized through a 2D/3D translation vector and 1/3 Euler angles. In contrast, nonrigid methods have usually a much higher number of DoF in order to model more complex transformations. Consequently, the estimation of a nonrigid transformation field requires a much larger number of correspondences. Another challenging problem is the choice of a proper representation of the transformation field: on the one hand, it must be flexible enough to model systematic discrepancies between the point clouds, and on the other hand, overfitting and excessive computational costs must be avoided.
-
Traditional vs. learning based: Traditional methods are based entirely on handcrafted, mostly geometric relationships. This may also include the design of handcrafted descriptive point features used in the matching step. Recent advances in the field of point cloud registration, however, have been clearly dominated by deep-learning-based methods—a recent survey is given by [11]. Such methods are especially useful for finding a coarse initial transformation between the point clouds, i.e., to solve the coarse registration problem. In such scenarios, deep-learning-based methods typically lead to a better estimate of the initial transformation by automatically learning more robust and distinct point feature representations. This is particularly useful in the presence of repetitive or symmetric scene elements, weak geometric features, or low-overlap scenarios [6]. Recently, deep-learning-based methods have also been published for the nonrigid registration problem, e.g., HPLFlowNet [12] or FlowNet3D [13].
-
Pairwise vs. multiview: The majority of registration algorithms can handle a single pair of point clouds only. In practice, however, objects are typically observed from multiple viewpoints. As a consequence, a single point cloud generally overlaps with >1 other point clouds. In such cases, a global (or joint) optimization of all point clouds is highly recommended. Such an optimization problem is often interpreted as a graph where each node corresponds to an individual point cloud with associated transformation and the edges are either the correspondences themselves (single-step approach, e.g., [14]) or the pairwise transformations estimated individually in a preprocessing step (two-step approach, e.g., [15][16][17]).
-
Full overlap vs. partial overlap Many algorithms (particularly also in the context of nonrigid transformations, e.g., [18][19]) assume that the two point clouds are fully overlapping. However, in practice, a single point cloud often corresponds only to a small portion of the observed scene, e.g., when scanning an object from multiple viewpoints. It is particularly difficult to find valid correspondences (under the assumption that the point clouds are not roughly aligned) in low-overlap scenarios, e.g., point clouds with an overlap below 30%. This challenge is addressed by [7] and the therein introduced 3DLoMatch benchmark.
-
Approximative vs. rigorous: Most registration algorithms are approximative in the sense that they use the 2D or 3D point coordinates as inputs only and try to minimize discrepancies across overlapping point clouds by applying a rather simple and general (rigid or nonrigid) transformation model. Ref. [20] describes this group of algorithms as rubber-sheeting coregistration solutions. In contrast, rigorous solutions try to model the point cloud generation process as accurately as possible by going a step backwards and using the sensor’s raw measurements. The main advantage of such methods is that point cloud discrepancies are corrected at their source, e.g., by sensor self-calibration of a miscalibrated lidar sensor [21]. Rigorous solutions are especially important in case of point clouds captured from moving platforms, e.g., robots, vehicles, drones, airplanes, helicopters, or satellites. In a minimal configuration, such methods simultaneously register overlapping point clouds and estimate the trajectory of the platform. More sophisticated methods additionally estimate intrinsic and extrinsic sensor calibration parameters and/or consider ground truth data, e.g., ground control points (GCPs), to improve the georeference of the point clouds. If point clouds need to be generated online, e.g., in robotics, this type of problem is addressed by SLAM (simultaneous localization and mapping), and especially lidar SLAM [22] and visual-lidar SLAM [23] methods. For offline point cloud generation, however, methods are often summarized under the term (rigorous) strip adjustment, as the continuous platform’s trajectory is often divided into individual strips for easier data handling—an overview can be found in [20][24].
References
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Robotics-DL Tentative; International Society for Optics and Photonics: Bellingham, WA, USA, 1992; pp. 586–606.
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155.
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. A Correspondence Framework for ALS Strip Adjustments based on Variants of the ICP Algorithm. PFG Photogramm. Fernerkund. Geoinf. 2015, 2015, 275–289.
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152.
- Pomerleau, F.; Colas, F.; Siegwart, R. A review of point cloud registration algorithms for mobile robotics. Found. Trends Robot. 2015, 4, 1–104.
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote. Sens. 2020, 163, 327–342.
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. Predator: Registration of 3D point clouds with low overlap. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4267–4276.
- Li, L.; Wang, R.; Zhang, X. A tutorial review on point cloud registrations: Principle, classification, comparison, and technology challenges. Math. Probl. Eng. 2021, 2021, 9953910.
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A globally optimal solution to 3D ICP point-set registration. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2241–2254.
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017.
- Zhang, Z.; Dai, Y.; Sun, J. Deep learning based point cloud registration: An overview. Virtual Real. Intell. Hardw. 2020, 2, 222–246.
- Gu, X.; Wang, Y.; Wu, C.; Lee, Y.J.; Wang, P. HPLFlowNet: Hierarchical Permutohedral Lattice FlowNet for Scene Flow Estimation on Large-scale Point Clouds. In Proceedings of the 2019 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019.
- Liu, X.; Qi, C.R.; Guibas, L.J. FlowNet3D: Learning Scene Flow in 3D Point Clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 529–537.
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. Rigorous Strip Adjustment of Airborne Laserscanning Data Based on the ICP Algorithm. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, II-3/W5, 73–80.
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Globally consistent registration of terrestrial laser scans via graph optimization. ISPRS J. Photogramm. Remote. Sens. 2015, 109, 126–138.
- Brown, B.; Rusinkiewicz, S. Global Non-Rigid Alignment of 3-D Scans. ACM Trans. Graph. 2007, 26, 1–9.
- Ressl, C.; Pfeifer, N.; Mandlburger, G. Applying 3D affine transformation and least squares matching for airborne laser scanning strips adjustment without GNSS/IMU trajectory data. In Proceedings of the ISPRS Workshop Laser Scanning 2011, Calgary, Canada, 29–31 August 2011.
- Myronenko, A.; Song, X.; Carreira-Perpinan, M. Non-rigid point set registration: Coherent point drift. Adv. Neural Inf. Process. Syst. 2006, 19, 1009–1016.
- Liang, L.; Wei, M.; Szymczak, A.; Petrella, A.; Xie, H.; Qin, J.; Wang, J.; Wang, F.L. Nonrigid iterative closest points for registration of 3D biomedical surfaces. Opt. Lasers Eng. 2018, 100, 141–154.
- Toth, C.K. Strip Adjustment and Registration. In Topographic Laser Ranging and Scanning-Principles and Processing; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 235–268.
- Lichti, D.D. Error modelling, calibration and analysis of an AM–CW terrestrial laser scanner system. ISPRS J. Photogramm. Remote. Sens. 2007, 61, 307–324.
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278.
- Zhang, J.; Singh, S. Visual-lidar odometry and mapping: Low-drift, robust, and fast. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181.
- Glira, P. Hybrid Orientation of LiDAR Point Clouds and Aerial Images. PhD Thesis, TU Wien, Vienna, Austria, 2018.
- Chui, H.; Rangarajan, A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Underst. 2003, 89, 114–141.
More
Information
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
716
Revisions:
2 times
(View History)
Update Date:
24 Nov 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




