Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Jingwen QI
 -- 1339 2023-11-10 14:24:34 |
2 update references and layout
Rita Xu
 -3 word(s) 1336 2023-11-13 02:59:53 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Qi, J.; Chen, T.; Zheng, J.; Wang, S. Port Call Optimization at a Ferry Terminal. Encyclopedia. Available online: https://encyclopedia.pub/entry/51426 (accessed on 16 November 2024).
Qi J, Chen T, Zheng J, Wang S. Port Call Optimization at a Ferry Terminal. Encyclopedia. Available at: https://encyclopedia.pub/entry/51426. Accessed November 16, 2024.
Qi, Jingwen, Tingting Chen, Jianfeng Zheng, Shuaian Wang. "Port Call Optimization at a Ferry Terminal" Encyclopedia, https://encyclopedia.pub/entry/51426 (accessed November 16, 2024).
Qi, J., Chen, T., Zheng, J., & Wang, S. (2023, November 10). Port Call Optimization at a Ferry Terminal. In Encyclopedia. https://encyclopedia.pub/entry/51426
Qi, Jingwen, et al. "Port Call Optimization at a Ferry Terminal." Encyclopedia. Web. 10 November, 2023.
Port Call Optimization at a Ferry Terminal
Edit
This entry is adapted from the peer-reviewed paper 10.3390/jmse11091644

Ferry shipping is an indispensable method of public transportation, especially in areas with well-developed river systems or coastal areas. The increasing demand for transport requires additional visits and introduces the problem of ship visit schedule engineering at ferry terminals with stochastic servicing time.

ferry shipping port call optimization visit schedule engineering

1. Introduction

Ferry shipping is an important component of public transportation servicing and plays an essential role in providing mobility for passengers in cities with coastal areas and river systems, such as Hong Kong [1] and Sydney [2]. In the management of ferry transportation, arranging ferry visits at the ferry terminal is a critical issue that potentially influences the service level and total profit of the ferry operation company. In practice, ferry servicing companies generally arrange ferry visits to provide the servicing for the ferry passengers at the ferry terminal. Specifically, a ferry visit denotes the process of a ferry arriving at the terminal, mooring at a berth, and servicing the disembarking and boarding passengers. The arrangement for ferry visits, including berthing time (ferry arrival times at the port), berthing locations (the berths that ferries moor at), and servicing time (time taken for disembarking and boarding), are generally stipulated in advance by the ferry visit plan, which is designed at the planning stage.
The servicing time of ferry visits is mainly affected by the numbers of boarding and disembarking passengers on each ferry visit. In practice, the number of passengers on each ferry visit is uncertain, which will result in the stochastic servicing time of ferry visits. This is due to the exact value of the passenger demand being unknown at the planning stage, and the servicing time of ferry visits is, thus, stochastic. The ferry servicing company allocates the servicing time for each ferry visit based on the historical passenger demand, which is referred to as allocated servicing time. The number of passengers taking the ferry will be revealed when the servicing is finished. Then, the actual servicing time of ferry visits will also be acquired. Figure 1 illustrates the ferry visit plan of three ferry visits at two berths, which is designed at the planning stage. Additionally, the actual servicing time of three ferry visits at the operational stage is also revealed in Figure 1. The x-axis and y-axis represent the time and berth, respectively. The actual servicing time and allocated servicing time are denoted by the solid red arrow line and the black one. For ferry visit 1, its actual servicing time (i.e., 25 min) far exceeds the allocated servicing time (i.e., 15 min). Then, ferry visit 2 cannot moor at berth 1 at its designed berthing time and serve passengers on time, thereby affecting the implementation of the ferry visit plan and reducing the servicing quality. For ferry visit 3, its actual servicing time (i.e., 20 min) is less than the allocated servicing time (i.e., 25 min), which will not affect the performance of the ferry servicing system. Therefore, the uncertain servicing time is an essential factor to consider at the planning stage since considering the servicing time uncertainty can make the ferry visit plan more applicable in practical operations.
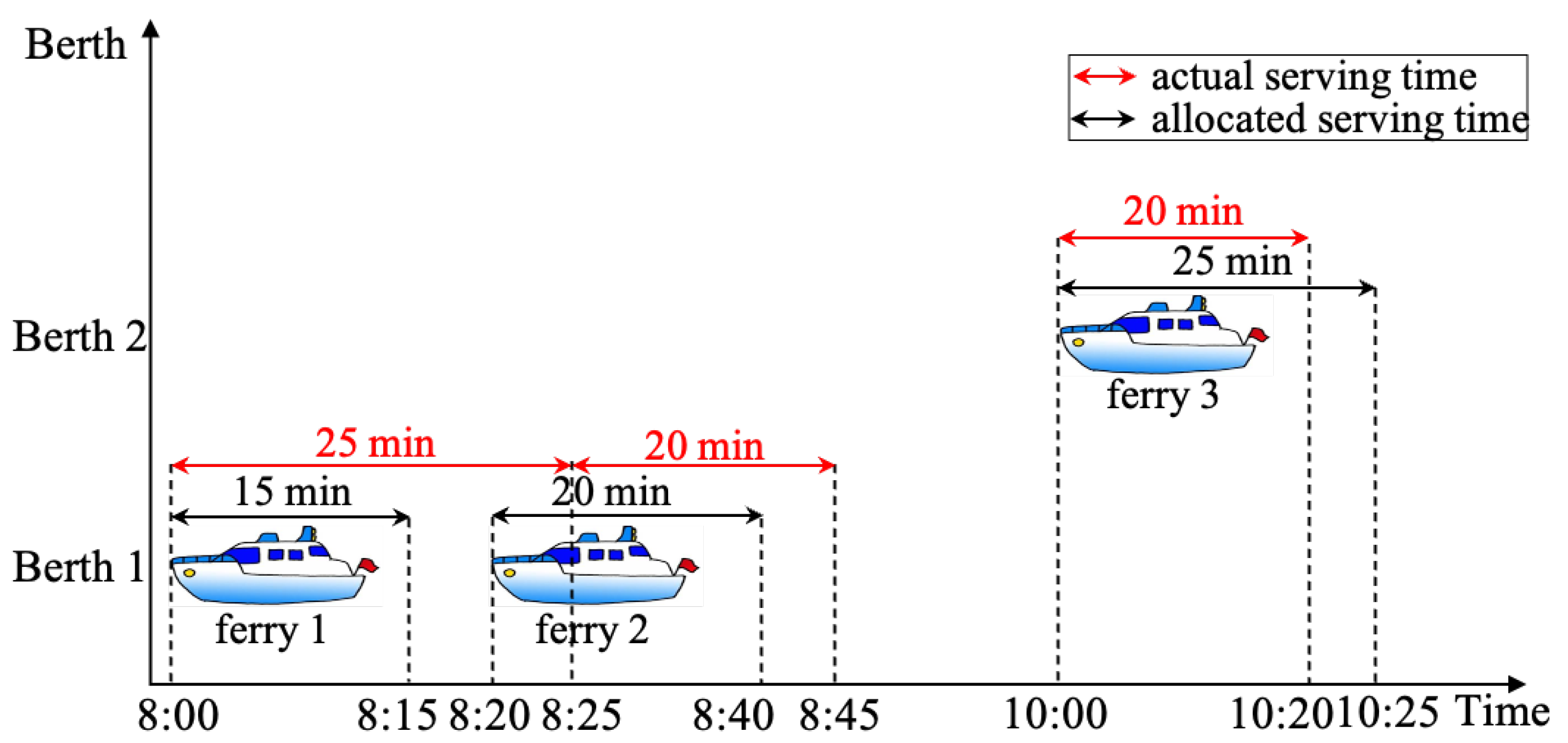
Figure 1. An illustration of actual and allocated servicing time.
In addition, the ferry passenger demand varies throughout the day. The ferry passenger demand during the peak hours tends to be higher than that during the flat hours. Correspondingly, the ferry visits operating during the peak hour typically serve more passengers and therefore bring higher revenue to the ferry servicing company. This varying revenue incurred by the time-dependent passenger demand is referred to as the time-dependent revenue in this study.

2. Port Call Optimization at a Ferry Terminal

Currently, there is only a fraction of papers focusing on the management problems regarding the ferry servicing. Among these works, the ferry network design problem (FNDP), which optimizes the ferry servicing network and passenger flow, is extensively studied. The FNDP was first proposed by [3]. They focused on a multiple origin–destination network flow problem with ferry capacity constraint. In [4], they extended [3] by introducing different ferry servicing types and passenger preferences with arrival time windows. Later, Ref. [5] studied a stochastic FNDP under uncertain demand and formulated a two-stage stochastic model. As an extension of the earlier works, Ref. [6] involved user equilibrium flows and hard capacity constraints. In [7], they proposed two robust optimization models for their FNDP. Recently, Ref. [8] utilized the maximum passenger utility spanning tree approach to optimize the connection between all pairs of ferry stations and the locations of hubs. In [9], they considered FNDP by introducing autonomous ferries. A two-step optimization approach was proposed to identify the optimal autonomous ferry servicing schedules. In their later study, Ref. [10], they focused on planning the ferry servicing schedule, which combined the dial-a-ride on-demand servicing and fixed schedule servicings simultaneously.
Although there has been some ferry-servicing-related research, the ferry visit planning problem that determines the berthing time, berthing location, and servicing time has rarely been studied. The ferry visit planning problem relates closely to the berth allocation problem (BAP), which allocates the berthing time and locations to the arriving vessels. In the past two decades, many researchers and practitioners have made great efforts to solve the BAP arising in the container port terminal. An early study was proposed by [11], and they focused on the objective of minimizing the overall staying time of vessels and dissatisfaction with vessel berthing order in the BAP. Later, some researchers studied the deterministic BAP by incorporating practical characteristics. For example, Ref. [12] investigated the integration of BAP, quay crane assignment problem, and yard allocation problem. In [13], they also studied an integrated problem that combined BAP with the quay crane allocation and scheduling problems. In practice, it is generally impossible for all the parameters to be fixed and known in advance. Uncertainties often arise in practical operations due to weather conditions and mechanical failures. A comprehensive review of the BAP under uncertainties was given by [14]. According to the review, uncertain factors regarding the arrival time [15][16][17][18], handling time [19][20][21][22], quay crane breakdown [23][24][25], and unscheduled vessel calling [26][27] were commonly considered in BAP problems. Arrival time and handling time are the most common uncertain parameters to be considered in the BAP. For the uncertain arrival time, Ref. [28] introduced a time buffer to handle the uncertain arrival time in the robust BAP. In [29], they proposed a robust model to optimize the berth allocation and quay crane assignment considering arrival time uncertainty. In [30], they addressed a berth allocation and assignment problem under uncertain vessel arrival time and port servicing time, where the cooperation among the liner carriers and that between port operator and liner shipping carriers were involved. For the uncertain handling time, Refs. [31][32] used the robust optimization method and distributionally robust optimization method to solve BAP, respectively. There are also many scholars who considered the uncertainties of arrival time and handling time simultaneously. In [22], they focused on the weekly berth and quay crane planning, where the berth position, berthing time, and quay crane assignment were optimized. In [33], they integrated BAP with yard space allocation, where the uncertain handling time was incurred by the uncertain number of loading and unloading containers. In [34], they optimized the berth allocation, assignment of tugboats, and the vessel sequence at the seaport.
To sum up, most of the existing literature has focused on either FNDP regarding the ferry servicing or BAP targeting the vessels transferring cargoes in the container port terminal. There is no paper studying the ferry visit planning problem that considers the deviation between the redesigned ferry visit plan and the current one, uncertain servicing time, and time-dependent revenue simultaneously. Firstly, the ferry passengers typically prefer the current ferry visit plan. If the redesigned ferry visit plan deviates from the current one, passengers’ travel plans will be affected. Hence, the deviation between the redesigned ferry visit plan and the current one should be considered. Secondly, the passenger demand is uncertain, resulting in an uncertain servicing time. Considering the servicing time uncertainty will make the ferry visit plan more applicable in practical operations. Thirdly, the passenger demand varies throughout the day, which introduces time-dependent revenue.

References

  1. Lau, Y.; Tam, K.; Ng, A.K. Ferry services and the community development of peripheral island areas in Hong Kong: Evidence from Cheung Chau. Isl. Stud. J. 2023, 1–25.
  2. Transportnsw.Info. Ferry|Transportnsw.Info. 2023. Available online: https://transportnsw.info/travel-info/ways-to-get-around/ferry#/ (accessed on 4 May 2023).
  3. Lai, M.; Lo, H.K. Ferry service network design: Optimal fleet size, routing, and scheduling. Transp. Res. Part A Policy Pract. 2004, 38, 305–328.
  4. Wang, D.Z.; Lo, H.K. Multi-fleet ferry service network design with passenger preferences for differential services. Transp. Res. Part B Methodol. 2008, 42, 798–822.
  5. Lo, H.K.; An, K.; Lin, W.H. Ferry service network design under demand uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2013, 59, 48–70.
  6. An, K.; Lo, H.K. Ferry service network design with stochastic demand under user equilibrium flows. Transp. Res. Part B Methodol. 2014, 66, 70–89.
  7. Ng, M.; Lo, H.K. Robust models for transportation service network design. Transp. Res. Part B Methodol. 2016, 94, 378–386.
  8. Bell, M.G.; Pan, J.J.; Teye, C.; Cheung, K.F.; Perera, S. An entropy maximizing approach to the ferry network design problem. Transp. Res. Part B Methodol. 2020, 132, 15–28.
  9. Aslaksen, I.E.; Svanberg, E.; Fagerholt, K.; Johnsen, L.C.; Meisel, F. Ferry service network design for kiel fjord. In Proceedings of the Computational Logistics: 11th International Conference, ICCL 2020, Enschede, The Netherlands, 28–30 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 36–51.
  10. Aslaksen, I.E.; Svanberg, E.; Fagerholt, K.; Johnsen, L.C.; Meisel, F. A combined dial-a-ride and fixed schedule ferry service for coastal cities. Transp. Res. Part A Policy Pract. 2021, 153, 306–325.
  11. Imai, A.; Nagaiwa, K.; Tat, C.W. Efficient planning of berth allocation for container terminals in Asia. J. Adv. Transp. 1997, 31, 75–94.
  12. Liu, C. Iterative heuristic for simultaneous allocations of berths, quay cranes, and yards under practical situations. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101814.
  13. Chargui, K.; Zouadi, T.; El Fallahi, A.; Reghioui, M.; Aouam, T. Berth and quay crane allocation and scheduling with worker performance variability and yard truck deployment in container terminals. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102449.
  14. Rodrigues, F.; Agra, A. Berth allocation and quay crane assignment/scheduling problem under uncertainty: A survey. Eur. J. Oper. Res. 2022, 303, 501–524.
  15. Han, X.L.; Lu, Z.Q.; Xi, L.F. A proactive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time. Eur. J. Oper. Res. 2010, 207, 1327–1340.
  16. Zhen, L.; Lee, L.H.; Chew, E.P. A decision model for berth allocation under uncertainty. Eur. J. Oper. Res. 2011, 212, 54–68.
  17. Umang, N.; Bierlaire, M.; Vacca, I. Exact and heuristic methods to solve the berth allocation problem in bulk ports. Transp. Res. Part E Logist. Transp. Rev. 2013, 54, 14–31.
  18. Ursavas, E.; Zhu, S.X. Optimal policies for the berth allocation problem under stochastic nature. Eur. J. Oper. Res. 2016, 255, 380–387.
  19. Zhen, L.; Chang, D.F. A bi-objective model for robust berth allocation scheduling. Comput. Ind. Eng. 2012, 63, 262–273.
  20. Shang, X.T.; Cao, J.X.; Ren, J. A robust optimization approach to the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 44–65.
  21. Xiang, X.; Liu, C.; Miao, L. A bi-objective robust model for berth allocation scheduling under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 294–319.
  22. Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389.
  23. Li, M.Z.; Jin, J.G.; Lu, C.X. Real-time disruption recovery for integrated berth allocation and crane assignment in container terminals. Transp. Res. Rec. 2015, 2479, 49–59.
  24. Liu, C.; Zheng, L.; Zhang, C. Behavior perception-based disruption models for berth allocation and quay crane assignment problems. Comput. Ind. Eng. 2016, 97, 258–275.
  25. Nourmohammadzadeh, A.; Voss, S. A robust multiobjective model for the integrated berth and quay crane scheduling problem at seaside container terminals. Ann. Math. Artif. Intell. 2022, 90, 831–853.
  26. Xiang, X.; Liu, C.; Miao, L. Reactive strategy for discrete berth allocation and quay crane assignment problems under uncertainty. Comput. Ind. Eng. 2018, 126, 196–216.
  27. Al-Refaie, A.; Abedalqader, H. Optimal berth scheduling and sequencing under unexpected events. J. Oper. Res. Soc. 2020, 73, 430–444.
  28. Park, H.J.; Cho, S.W.; Lee, C. Particle swarm optimization algorithm with time buffer insertion for robust berth scheduling. Comput. Ind. Eng. 2021, 160, 107585.
  29. Rodrigues, F.; Agra, A. An exact robust approach for the integrated berth allocation and quay crane scheduling problem under uncertain arrival times. Eur. J. Oper. Res. 2021, 295, 499–516.
  30. Guo, L.; Zheng, J.; Du, H.; Du, J.; Zhu, Z. The berth assignment and allocation problem considering cooperative liner carriers. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102793.
  31. Xiang, X.; Liu, C. An expanded robust optimisation approach for the berth allocation problem considering uncertain operation time. Omega 2021, 103, 102444.
  32. Agra, A.; Rodrigues, F. Distributionally robust optimization for the berth allocation problem under uncertainty. Transp. Res. Part B Methodol. 2022, 164, 1–24.
  33. Zhen, L.; Zhuge, D.; Wang, S.; Wang, K. Integrated berth and yard space allocation under uncertainty. Transp. Res. Part B Methodol. 2022, 162, 1–27.
  34. Liu, B.; Li, Z.C.; Wang, Y. A two-stage stochastic programming model for seaport berth and channel planning with uncertainties in ship arrival and handling times. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102919.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Operations Research & Management Science
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Jingwen Qi
,
Tingting Chen
,
Jianfeng Zheng
,
Shuaian Wang
View Times: 305
Revisions: 2 times (View History)
Update Date: 13 Nov 2023
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback