Adaptive Self-Organizing Map Using Optimal Control

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Mohamed Hussien Dessokey	--	2444	2023-10-19 10:42:20	\|
2	format correct	Catherine Yang	Meta information modification	2444	2023-10-19 10:46:01	\|

This entry is adapted from the peer-reviewed paper 10.3390/math11091995

The self-organizing map (SOM), which is a type of artificial neural network (ANN), was formulated as an optimal control problem. Its objective function is to minimize the mean quantization error, and the state equation is the weight updating equation of SOM. Based on the objective function and the state equations, the Hamiltonian equation based on Pontryagin’s minimum principle (PMP) was formed.

self-organizing map artificial neural network optimal control problem

1. Introduction

Deep Learning (DL), machine learning (ML), and other forms of Artificial Intelligence (AI) are on the rise in terms of solving numerous varieties of modern business problems and research, and they are used in engineering applications ^[1]. Clustering is a type of unsupervised learning method. This simply means that the references are drawn from datasets that contains input data without labeled responses. However, clustering is useful to find generative features, meaningful structure, and groupings that are inherent in a set of examples. The SOM algorithm was formulated as an optimal control problem with the objective to reduce the quantization error. Hence, giving more flexibility to engineers to manipulate many attributes of optimal control to be further improved, and thus enhancing SOM to obtain more accurate results in shorter periods of time. The slow learning process speed becomes an obstacle for SOM to be employed in real time and dynamic system applications. However, by applying optimal control with the aim to reduce the mean quantization error, a more accurate solution can be obtained. Basically, SOMs differ in the way that they use competitive learning and cooperative learning as opposed to error-correction learning. There are many methods that can be applied to solve optimal control problems. One of the methods that has obtained the most attention in recent years is Pontryagin’s minimum principle (PMP). PMP is used in the optimal control theory to identify the optimum feasible control for bringing a dynamical system from one state to another, especially in the face of limitations on the state or input controls. The proper Hamiltonian equation must be formulated to obtain the adjoint equation and switching function. SOM has been modeled as a PMP problem using MATLAB based on the SOM toolbox. This means that this algorithm implements a characteristic, non-linear projection from the high-dimensional space of input onto a low dimensional regular grid, which can be effectively utilized to visualize and explore the properties of the data ^[2]. The first issue with SOM, which may become a bottleneck for the analysis, is the data. To implement SOM, enough data for generating meaningful clusters are required, as insufficient or extraneous data might add additional randomness to the clusters ^[3]. This further motivates us to improve the SOM algorithm using the optimal control as the current data analysis, which requires a large amount of data to be clustered. When training with huge amounts of data, the training tends to be slower ^[4]. However, once the training has been completed, new data can be mapped quickly to the SOM. The error measured during the training period can be improved to obtain an improved clustering. The quantization error will be addressed in this study and improved using the optimal control. Generally, the smaller the quantization error, the better the quantization ^[5]. Moreover, in ^[6], a synthetic neural network-based SOM for the classification problem of Coronary Heart Disease (CHD) was proposed. The simulation results show a better accuracy and error rate compared to another dataset. The authors of ^[7] introduced a path planning and control method for a humanoid robot, which requires a path planning system that can take data representing an external sensor, extract the connected paths, and link the paths together to form the Cartesian motion for the robotic system. A comparison of the back-propagation model and the SOMs model in terms of planning the motion in a humanoid robot is presented in this study, showing that SOM performs better and achieves better results. Color image segmentation is based on the SOM and K-means algorithms proposed by ^[8]; the outcomes show that SOM performs better in terms of discriminating the main features of the image, whereas the results from the K-means algorithm present the minimum number of the non-connected regions corresponding to the objects that are contained in the image. SOM also performs better in terms of noise toleration and topology preservation. In ^[9], the researchers argue that SOM dataset can be efficiently used for clustering as it can classify image objects with an unknown probability distribution without requiring the determination of complicated parameters. They defined a hierarchical SOM and used it to construct the clustering method. The appropriate number of classes and the hierarchical relations in the datasets can be effectively revealed through SOM. However, the error loss and the learning speed are not discussed in this study. In ^[10], a classification system based on a Principal Component Analysis Convolutional Network (PCN) was proposed, where convolutional filters are used to extract discriminative and hierarchical features. According to the experimental results, the proposed PCN system is feasible for real-time applications because of its robustness against various challenging distortions, such as translations, rotations, illumination conditions, and noise contaminations. In general, optimal control problems consist of mathematical expressions that include the objective function and all constraints, and are collectively known as optimization problems. The constraints include the state equation, any conditions that must be satisfied at the beginning and end of the time horizon, and anything that restricts choices between the beginning and end. At a minimum, dynamic optimization problems must include the objective function, the state equation(s), and initial conditions for the state variables ^[11]. It is interesting to evaluate the performance of metaheuristics in solving multi-objective fed-batch fermentation problems. Therefore, the problem that is being addressed in this work is to reduce the mean quantization error of SOM by formulating the conventional self-organizing map algorithm as the optimal control problem. The mean quantization error equation becomes the objective function to be minimized and the online mode weight updating equation becomes the state equation. In terms of new designs of the Power Amplifier (PA) for next-generation wireless communication, the researchers in ^[12] suggested a new approach to enhance the performance of the PAs in the context of efficiency and linearity. The aim is to eliminate the design cost and space. Additionally, the authors of ^[13] explored the effect of two classes of grass-trimming machine engine noise on the operator in the natural working environment. The experimental results indicate that the sound pressure level of the grass trimmer machine’s engine exceeds the noise limit recommended for other machine engines by approximately 98 h per week. The authors of ^[14] carried out a Genetic Algorithm (GA) to determine the optimal chip placement of the Multi-Chip Model (MCM) and Printed Circuit Board (PCB) under certain thermal constraints. The comparison results of the optimal placement utilizing a GA with other placement techniques were elaborated. However, the evaluation is valid under steady-state conditions and for MCM or PCB constant characteristics. The chip/component can only be a specific standard size. Furthermore, ^[15] developed a Variable Order Ant System (VOAS) to optimize the area and wirelength by combining the VOAS with a floorplan model called a Corner List (CL), where two classes of ants are introduced to determine the local information in this study. The results showed that VOAS has better improvement, purely in terms of area optimization and the composite function of the area and wirelength compared to other benchmark techniques. The author of ^[16] proposed a Hierarchical Congregated Ant System (H-CAS) to perform a variable order bottom-up hierarchical placer that can generate compact placement in a chip layout for hard and soft modules of floor planning. The empirical outcomes demonstrated that H-CAS performs a more efficient placer than state-of-the-art technique in terms of the circuit size, complexity increase, stability, and scalability. Additionally, H-CAS excels in all other techniques for higher-size issues in area minimization. Additionally, a novel non-linear consequent part recurrent T2FS (NCPRT2FS) for the prediction and identification of renewable energy systems was proposed ^[17]. Furthermore, this study took the advantages of the non-linear consequent and recurrent structure, in order to create a better model for highly non-linear systems and assist with the proper selection for the identification of system dynamics, respectively. The simulations indicated that the NCPRT2FS based on the backpropagation algorithm and adaptive optimization rate performed better than the other techniques in terms of identifications with fewer errors and a smaller number of fuzzy rules. Another work proposed a sequential quadratic Hamiltonian (SQH) algorithm for solving non-smooth supervised learning problems (SLPs) where the stability of the proposed algorithm is theoretically investigated in the framework of residual neural networks with a Runge–Kutta structure; a numerical comparison of the SQH algorithm with the extended method of successive approximation (EMSA) was involved. The numerical results showed a better performance of the SQH algorithm in terms of the efficiency and robustness of the training process ^[18]. On the hand, a sequential quadratic Hamiltonian (SQH) scheme for solving non-smooth quantum optimal control problems was discussed in ^[19], where the numerical and theoretical outcomes that were presented demonstrate the ability of the SQH scheme to solve control problems that are governed by quantum spin systems.

2. Artificial Neural Networks

Artificial neural networks (ANNs) are a machine approximation of biological neural networks such as the connective structure of the human brain for the purpose of learning. Moreover, the ANN algorithm is divided into supervised learning, unsupervised learning, and semi-supervised learning. In supervised learning, models are trained using labeled data including the required output. While unsupervised learning does not include output variables, which means that the data are not labeled. On the other hand, a combination of both supervised and unsupervised learning is called semi-supervised learning. This type of learning includes unlabeled data and labeled data. Additionally, this type of learning is useful in cases where labelling all the data would be time consuming, cost-prohibitive, or infeasible ^[10]^[20].

3. Clustering

Clustering is a basic challenge in many data-driven application fields, and the quality of the data representation has a significant impact on the performance of clustering. As a result, feature modifications, whether linear or non-linear, have been extensively employed to develop a better data representation for clustering. However, clustering using K-means tends to be slower and provide higher errors. Hence, the self-organization map is highly beneficial in clustering as it typically produces fewer errors compared to K-means because it preserves the topology of its nodes on the dataset ^[16]^[21].

4. Self-Organization Map

A self-organization map (SOM) is a type of ANN that is taught using unsupervised learning to generate a small, discernible representation of the training samples’ input space, called a map, which is a way to reduce dimensionality. Moreover, SOM mapping processes begin with weight vector initialization. Every weight vector has neighboring weights that are close to it. The picked weight is rewarded by the fact that the randomly picked sample vector is more similar. The neighbors of that weight are also rewarded by being able to become more like the chosen sample vector. Furthermore, SOM is defined as an unsupervised class based on competitive learning, where the output neurons compete amongst themselves to be activated ^[3]. Meanwhile, back-propagation is applied in supervised learning to learn the weights of a multi-layer neural network with a fixed architecture. A network forward propagation of activation produces an output and a backward propagation produces an error to find the weight changes. In the study, the incrementing number of hidden neurons leads to the better approximation in the SOM and more neurons are used in SOM compared to back-propagation. Moreover, there is less risk of local minima, stable convergence, and faster training. The SOM may be considered a good tool for classification and clustering processes. Generally, the SOM consists of two layers, the input layer and the output layer. The difficulties faced when deploying SOM algorithm are that in the normalization of the input’s space, the classifications lose their precision and the neurons cannot differentiate between the original inputs. Moreover, the standardization of the input vectors may provoke serious problems if a similarity or linearity between the inputs parameters are detected. To overpass this inconvenience, the use of supplementary tools that can handle the input’s space without affecting the classification ability, such as PCA, is required ^[22]. The SOM toolbox has been introduced as a tool in the visualization of high-dimensional data. However, the SOM toolbox generally facilitates the utilization of the SOM algorithm, encompassing data formatting, construction, preprocessing, initialization, and training using SOM. The default topology of the SOM is hexagonal ^[23]^[24].

5. Optimal Control Problem Using Pontryagin’s Minimum Principle

The optimal control way of solving the optimization problem makes use of Pontryagin’s minimum principle. In the optimal control theory, the variable

λ_{t}

is called the costate variable.

λ_{t}

is equal to the marginal value of relaxing the constraint, which means that

λ_{t}

is equal to the marginal value of the state variable

x_{t}

. The costate variable plays a critical role in dynamic optimization.

The Hamiltonian is a function employed to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain period ^[25]^[26]. The Hamiltonian equation can be written as follows:

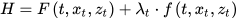where

F (t, x_{t}, z_{t})

is the objective function and

f (t, x_{t}, z_{t})

is the state equation,

x_{t}

is the state variable(s) and

z_{t}

is the set of choice variable(s). For the solution using the Hamiltonian to yield the same minimum, the following conditions must be satisfied:

$\frac{\partial H}{\partial z_{t}} = 0$ , the Hamiltonian should be minimised with respect to the control variable at every point in time.
$\frac{\partial H}{\partial x_{t}} = λ_{t - 1} - λ_{t},$ the costate variable changes over time at a rate equal to minus the marginal value of the state variable to the Hamiltonian.
$\frac{\partial H}{\partial λ_{t}} = x_{t + 1} - x_{t}$ , the state equation must always be satisfied.

For this work, the first-order necessary condition is sufficient, as the problem is solved using Pontryagin’s maximum principle (PMP). On the other hand, the second-order sufficient condition is not always necessary in the PMP of the optimal control. The second-order sufficient condition is a more stringent condition that provides a sufficient condition for optimality by analyzing the convexity of the Hamiltonian. However, it is not necessary for the application of the maximum principle. This has been discussed in several pieces of literatures on optimal control theory, such as ^[27]^[28]. In particular, ref. ^[27] states that “it is generally not necessary to determine whether the second-order conditions hold” for the maximum principle to be applicable. Similarly, Sanders notes that “it is important to keep in mind that the maximum principle is concerned only with first-order conditions”.

Therefore, while the second-order sufficient condition can provide a useful criterion for determining optimality in some cases, it is not necessarily important in the context of the maximum principle of optimal control.

References

Soon, F.C.; Khaw, H.Y.; Chuah, J.H.; Kanesan, J. Vehicle logo recognition using whitening transformation and deep learning. Signal Image Video Process. 2018, 13, 111–119.
Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600.
Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480.
Wehrens, H. Data mapping: Linear methods versus nonlinear techniques. Compr. Chemom. 2009, 2, 619–633.
Sun, Y. On quantization error of self-organizing map network. Neurocomputing 2000, 34, 169–193.
Widiyaningtyas, T.; Zaeni, I.A.E.; Wahyuningrum, P.Y. Self-Organizing Map (SOM) For Diagnosis Coronary Heart Disease. In Proceedings of the 2019 4th International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 20–21 November 2019; pp. 286–289.
Wankhede, S.B. Study of back-propagation and self organizing maps for robotic motion control: A survey. In Proceedings of the 2017 International Conference on Trends in Electronics and Informatics (ICEI), Tirunelveli, India, 11–12 May 2017; pp. 537–540.
Ristic, D.M.; Pavlovic, M.; Reljin, I. Image segmentation method based on self-organizing maps and K-means algorithm. In Proceedings of the 2008 9th Symposium on Neural Network Applications in Electrical Engineering, Belgrade, Serbia, 25–27 September 2008; pp. 27–30.
Zhang, X.-Y.; Chen, J.-S.; Dong, J.-K. Color clustering using self-organizing maps. In Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007; pp. 986–989.
Soon, F.C.; Khaw, H.Y.; Chuah, J.H.; Kanesan, J. Semisupervised PCA convolutional network for vehicle type classification. IEEE Trans. Veh. Technol. 2020, 69, 8267–8277.
Chong, E.K.; Zak, S.H. An Introduction to Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 75.
Eswaran, U.; Ramiah, H.; Kanesan, J. Power amplifier design methodologies for next generation wireless communications. IETE Technol. Rev. 2014, 31, 241–248.
Badruddin, I.A.; Hussain, M.K.; Ahmed, N.S.; Kanesan, J.; Mallick, Z. Noise characteristics of grass-trimming machine engines and their effect on operators. Noise Health 2009, 11, 98–102.
Jeevan, K.; Quadir, G.; Seetharamu, K.; Azid, I. Thermal management of multi-chip module and printed circuit board using FEM and genetic algorithms. Microelectron. Int. 2005, 22, 3–15.
Hoo, C.-S.; Jeevan, K.; Ganapathy, V.; Ramiah, H. Variable-Order ant system for VLSI multiobjective floorplanning. Appl. Soft Comput. 2013, 13, 3285–3297.
Hoo, C.-S.; Yeo, H.-C.; Jeevan, K.; Ganapathy, V.; Ramiah, H.; Badruddin, I.A. Hierarchical congregated ant system for bottom-up VLSI placements. Eng. Appl. Artif. Intell. 2013, 26, 584–602.
Tavoosi, J.; Suratgar, A.A.; Menhaj, M.B.; Mosavi, A.; Mohammadzadeh, A.; Ranjbar, E. Modeling renewable energy systems by a self-evolving nonlinear consequent part recurrent type-2 fuzzy system for power prediction. Sustainability 2021, 13, 3301.
Hofmann, S.; Borzì, A. A sequential quadratic hamiltonian algorithm for training explicit RK neural networks. J. Comput. Appl. Math. 2022, 405, 113943.
Breitenbach, T.; Borzì, A. A sequential quadratic Hamiltonian scheme for solving non-smooth quantum control problems with sparsity. J. Comput. Appl. Math. 2020, 369, 112583.
Alkawaz, A.N.; Abdellatif, A.; Kanesan, J.; Khairuddin, A.S.M.; Gheni, H.M. Day-Ahead Electricity Price Forecasting Based on Hybrid Regression Model. IEEE Access 2022, 10, 108021–108033.
Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514.
Lasri, R. Clustering and classification using a self-organizing MAP: The main flaw and the improvement perspectives. In Proceedings of the 2016 SAI Computing Conference (SAI), London, UK, 13–15 July 2016; pp. 1315–1318.
Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. Self-organizing map in Matlab: The SOM Toolbox. In Proceedings of the Matlab DSP Conference, Espoo, Finland, 16–17 November 1999; pp. 16–17.
MathWorks. Plotsomhits. 2022. Available online: https://www.mathworks.com/help/deeplearning/ref/plotsomhits.html (accessed on 1 November 2022).
Ferguson, B.S.; Lim, G.C.; Lim, G.C. Introduction to Dynamic Economic Models; Manchester University Press: Manchester, UK, 1998.
Alkawaz, A.N.; Kanesan, J.; Khairuddin, A.S.M.; Chow, C.O.; Singh, M. Intelligent Charging Control of Power Aggregator for Electric Vehicles Using Optimal Control. Adv. Electr. Comput. Eng. 2021, 21, 21–30.
Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: North Chelmsford, MA, USA, 2004.
Macki, J.; Strauss, A. Introduction to Optimal Control Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Chemistry, Organic

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ali Najem Alkawaz

Jeevan Kanesan

Irfan Anjum Badruddin

Sarfaraz Kamangar

Mohamed Hussien Dessokey

Maughal Ahmed Ali Baig

N. Ameer Ahammad

View Times: 170

Update Date: 19 Oct 2023

Table of Contents

Video Upload Options

Confirm