Characteristics and Models of Viscoelastic Materials

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Zdzisław Mikołaj Pawlak	--	3242	2023-10-07 11:00:52	\|
2	layout	Jessie Wu	+ 2 word(s)	3244	2023-10-08 02:54:08	\| \|
3	corrections	Przemysław Litewka	-32 word(s)	3215	2023-10-09 10:52:19	\|

This entry is adapted from the peer-reviewed paper 10.3390/buildings13092223

Viscous and viscoelastic (VE) dampers have been extensively used for the seismic response control in buildings. Such devices are exploited with good results in newly erected structures and also in retrofit projects.

viscoelastic dampers and layers systems with viscoelastic elements free steady-state and transient vibrations

1. General Characteristics of Classical and New Viscoelastic Materials Used in Dampers and Layers

Viscoelastic (VE) materials dissipate energy through forces related to the velocity of motion and the involved damping occurs for different levels of excitations. Fluid and solid VE materials are applied in the passive control systems. Various highly viscous fluids, such as Polydimethylsiloxane (C₂H₆OSi) (see ^[1]), are used in the fluid dampers ^[2]^[3]^[4]. Typically, these dampers have the form of a cylinder filled with a VE fluid and a perforated piston. Its movement causes the liquid to flow through its orifices and thus the damping force is generated. There exist also semi-active or active control systems using magnetorheological and electrorheological fluids. In this case the magnetic or electric field is applied when the fluid flows through the orifices to change its rheological properties very quickly in time. The literature concerning mechanical problems for these types of systems is very broad and is outside the scope of the present entry. Interested readers can consult the review papers ^[5]^[6] where an introduction to this problem and an overview of the literature are presented.

Many types of polymeric materials, classified as solid VE, exhibit a damping behavior. In ^[7], one can find a list of several categories of polymers available for manufacturing of stable material damping systems. Polymers are materials composed of long, intertwined and cross-linked molecular chains. Elastomers are an important class of polymers and they are very often used in VE damping devices. Many types of rubbers represent an important subclass. Elastomers exhibit the capability of reversible deformation under an action of mechanical forces, while maintaining the structural continuity. When subjected to loading, an elastomer can deform in a wide displacement range and can dissipate energy through shear deformation, both axial and rotational ^[8]. Each solid VE material exhibits two fundamental rheological phenomena, i.e., creep and stress relaxation ^[7]^[8]. Creep is the tendency to undergo a slow increase in deformation under the action of a constant mechanical stress. It occurs as a result of a long-term exposure to high levels of stress which are still below the yield strength of the material. Relaxation is a phenomenon which is characterized by decreasing the existing stress when the material is subjected to a constant state of strain. In dynamics, the most important mechanical properties of solid VE materials are the storage modulus, which characterizes the stiffness of the material, and the loss modulus and the loss factor, which are the measures of damping properties. All these parameters are dependent on the excitation frequency, temperature and magnitude of vibration amplitudes, if the amplitudes are large enough. A general trend is that the storage modulus and the loss factor increase with increasing excitation frequencies. The impact of ambient temperature on the properties of solid VE materials is a more complex problem. At low ambient temperature conditions, called the glassy region, the polymer molecules are frozen and the VE material has a high stiffness, a large storage modulus and a small loss factor. As the temperature increases some of the polymer molecules begin to wiggle around. This range of temperature is called the transition region. In the transition region, the storage modulus decreases with temperature but the loss factor reaches its maximum at a certain value of temperature. With the further increase in temperature, the VE materials enter the rubbery region. Now, both the storage modulus and the loss factor decrease with temperature. These tendencies are schematically illustrated in Figure 1. The combination of properties of VE materials in the transition region is most appropriate for the dissipation of energy and is exploited in VE dampers and layers. Moreover, the temperature of VE materials can increase due to self-heating, which was experimentally and numerically studied, for example, in ^[9]^[10].

Figure 1. Temperature dependence of the storage modulus and the loss factor.

In Figure 1, the generic curves of the storage modulus and the loss factor versus temperature are show nnot representing any specific experimental data. However, qualitatively similar experimental results can be found, for example, in the papers ^[11]^[12].

VE materials used in dampers and layers must satisfy some specific requirements. First of all, they must feature a large loss factor. They must also be characterized by high heat dissipation and low heat generation properties. Another requirement is a stable working performance in a wide range of temperatures. The VE material should also be durable, i.e., resistant to corrosion, oxidation, and fatigue. All these requirements are not easily satisfied by real VE materials. For this reason, modified rubbers are often used in VE dampers. Fillers, such as silica, silicate, clay and carbon black, which is most popular, are used for improving the properties of rubber. A high damping rubber with a high deformation capacity produced in China was investigated by Chen et al. in ^[13]. Wu et al. ^[14] found that the addition of small organic molecules to rubber can greatly improve its loss factor. Several types of VE materials with various types of matrices based on nitrile butadiene rubber and silicone rubber were proposed for dampers in ^[15]. Experimental results showed that such VE materials had a high energy dissipation capacity and featured stable performance. A high damping acrylate-based VE material was described by Xu et al. in ^[16], who investigated the dynamic properties of acrylate VE dampers at different temperatures, frequencies and amplitudes. Experimental results showed that these dampers had an excellent damping capacity. The feasibility of using a blended rubber matrix to enlarge the working temperature range of VE materials was investigated in ^[17]. It was found that the loss factor was almost doubled in comparison with a single rubber matrix. In the paper by Ge et al. ^[18], results of an experimental study of nitrile-butadiene rubber with different damping modifiers were presented. The obtained VE material was found to possess excellent damping properties. In ^[19], some other papers about the modification of rubbers were reviewed. The influence of aging on some VE materials used in dampers was experimentally investigated in ^[19]. Experimental results concerning the dynamic properties of the VE material were also presented by Xu et al. ^[20]. Very recently, the feasibility of using a novel hyperelastic and high-damping rubber material was experimentally investigated in ^[21] in order to determine its damping ratio, compressibility, and elasticity behavior under axial dynamic load. The results showed that the considered material could provide a high damping ratio between 10% and 13%. An elastomer compound with a high damping capacity and a relatively low stiffness was tested by He et al. ^[22]. The obtained results indicated that the tested VE material had excellent deformability with a strain amplitude of over 500% combined with a high-stress strength. Moreover, the examined VE material featured a superior energy dissipation capacity with a maximum viscous damping ratio of up to 30%. Low frequency dependence under cyclic dynamic loading and a better energy dissipation capacity at high loading frequency were also observed. Results from the dynamic testing of a thermoplastic elastomer of the olefin-styrene series were presented in ^[23]. The considered material exhibited a low temperature dependence. The mechanical properties of the VE material and their dependence on the amplitude and frequency of excitation of the material, as well as on its temperature, were determined.

2. Models of Viscoelastic Materials and Identification of Theirs Parameters

Various studies on materials with rheological properties were conducted in the 19th century by Ludwig Boltzmann, James Clark Maxwell, and Lord Kelvin ^[24]. The linear theory of viscoelasticity is founded on the Boltzmann superposition principle, according to which each load step makes an independent contribution to the final state ^[25]. This principle is most often used to formulate the integral representation of linear viscoelasticity. However, the more common way of describing linear viscoelasticity is the differential approach, where the rheological properties are represented by an appropriate combination of simple mechanical elements: springs and dashpots. The spring is a symbol of a purely elastic solid obeying Hooke’s law, whereas the dashpot, as a damping element, symbolizes the properties of an ideal Newtonian viscous fluid. A number of individual mechanical elements and the way they can be connected are illustrated graphically in Figure 2.

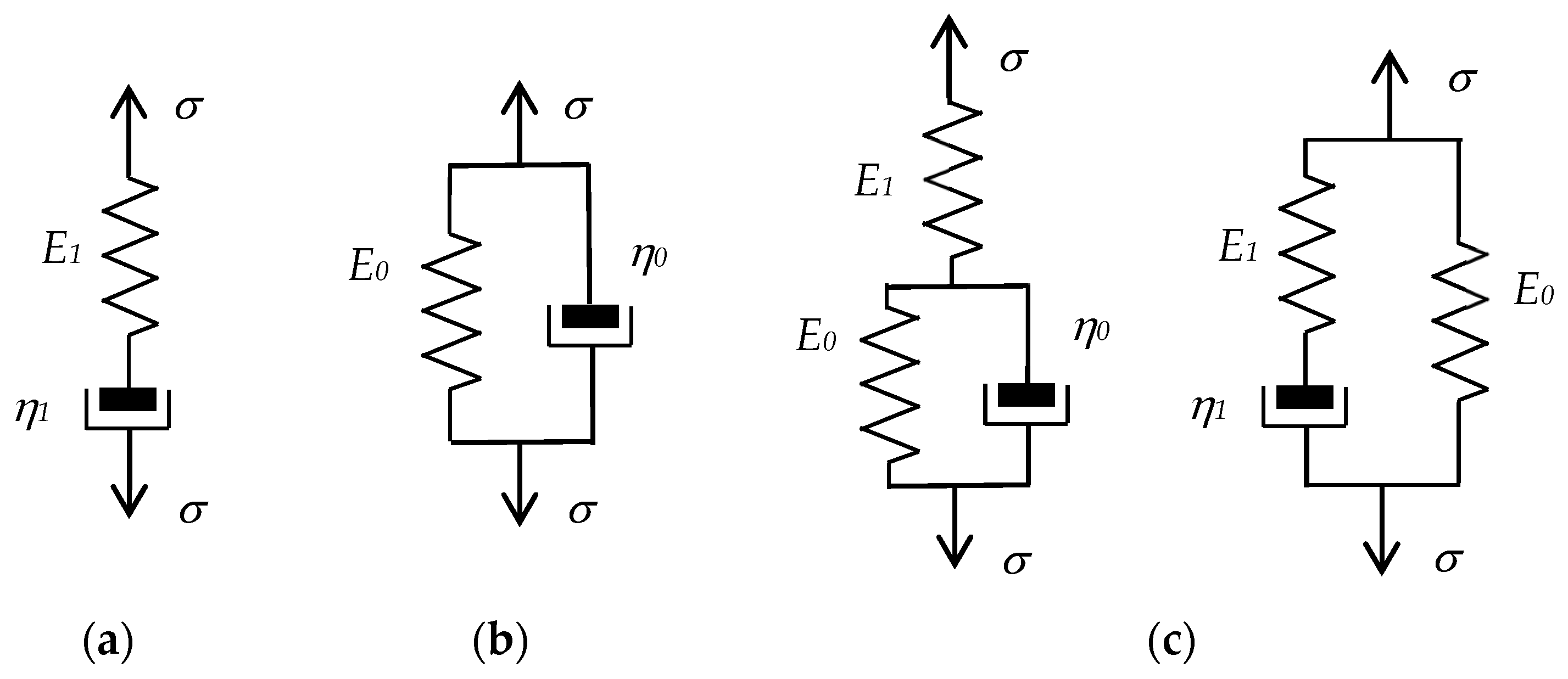
Figure 2. Basic classical mechanical models of VE materials: (a) Maxwell model, (b) Kelvin–Voigt model, (c) standard three-parameter models.

The basic classical mechanical models of VE materials are composed of an elastic spring and a viscous damping element connected in series for the Maxwell model (see Figure 2a) or in parallel for the Kelvin–Voigt model (Figure 2b). In Figure 2,

σ

stands for stress, E_i is the coefficient of elasticity, and η_i is the coefficient of viscous damping.

However, the basic models are insufficient to fully describe the dynamic behavior of VE materials and they are only effective in a small frequency range. The Maxwell model fails to reproduce the phenomenon of creep ^[25], whereas the Kelvin–Voigt model does not describe the relaxation behavior well and represents the rheological properties poorly, even for uncomplicated materials such as rubbers ^[26].

By connecting a spring in series with a Kelvin–Voigt element or in parallel with a Maxwell element, the three-element elastic models ^[27], also called standard linear solid models, are obtained; see Figure 2c. These models are also referred to as standard three-parameter Voigt and Maxwell models ^[28] or standard linear Kelvin and Maxwell solid models ^[29], respectively. They both exhibit the same mechanical behavior although their structure is different. According to the principle of conversion, one model can be replaced with another and they can be described by the same equation ^[29]^[30].

In the classical approach to modeling of linear VE behavior, the stress–strain equation can be represented in a general form by differential operators ^[31].

\sum_{m = 0}^{M} a_{m} \frac{d^{m} σ (t)}{d t^{m}} = \sum_{n = 0}^{N} b_{n} \frac{d^{n} ε (t)}{d t^{n}}

where σ(t) and ε(t) are the functions of stress and strain varying in time t, a_m and b_m are the model coefficients and M and N are the corresponding numbers of the series components.

More complex four-parameter classical models are formed as a combination of basic models. The Burgers model ^[32] is built from the Kelvin–Voigt model connected in series with the Maxwell model. On the other hand, a parallel connection leads to the standard model, also known as the Zener model ^[33]. These models more realistically represent rheological properties of a VE material with a good trade-off between complexity and accuracy ^[26]. The Burgers model is widely used in road construction engineering because it describes in the best way the creep and the relaxation characteristics of asphalt composite concrete.

Three- or four-element models can describe the dynamic behavior of VE materials with a good approximation only for selected small ranges of temperature and vibration frequencies. Representation of rheological properties of VE materials over a wider temperature or frequency range requires models with a large or even infinite number of mechanical elements, i.e., springs and dashpots ^[25]^[35].

By combining a much larger number of basic models, generalized series/parallel models are obtained, which have two forms: the generalized Maxwell-type models, useful for the analysis of VE fluids and rubber-like materials, and the generalized Voigt-type models, which should be used for VE solids ^[24]. If a spring is added in parallel to the generalized Maxwell model, as in Figure 3, an extended model is obtained that is suitable for solving problems in the dynamics of solids, including VE materials ^[28]^[36].

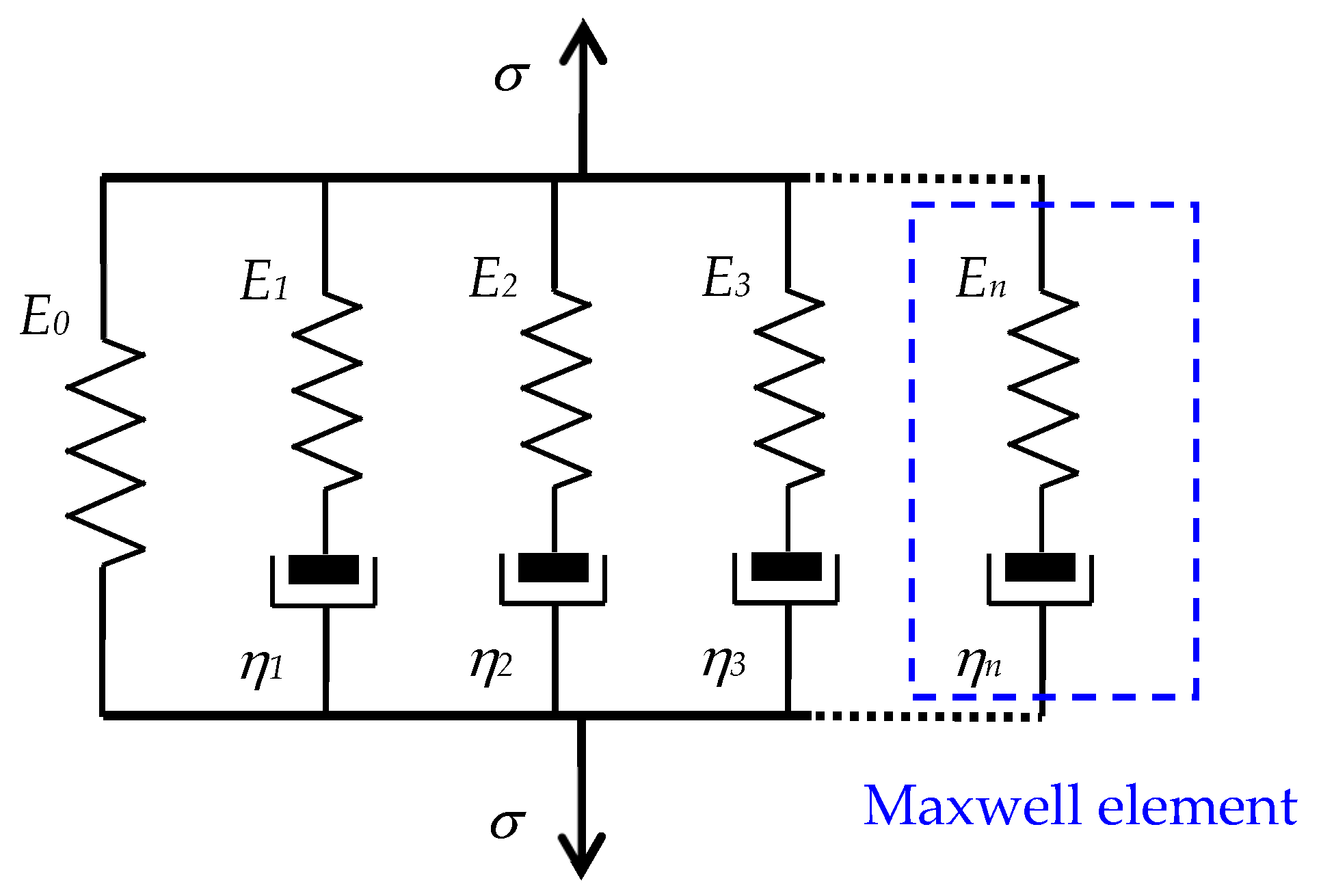
Figure 3. The generalized Maxwell model with an additional spring.

A highly versatile and accurate model can be built by combining basic and generalized models in an arbitrary way. For any model composed of springs and dashpots, the constitutive relation can be written in a form of a differential equation. The advantage of the differential equations approach is that each model can be easily understood and interpreted physically. The disadvantage is that more advanced models are described by a higher-order differential equation, what complicates the calculations, and it is very difficult or sometimes impossible to identify the parameters of the model adopted for the real material ^[26]^[37].

A way to overcome these problems is the use of fractional calculus to describe rheological phenomena ^[38]^[39]. Dashpots used in the classical rheological models can be replaced with the so-called spring-pot elements, i.e., the Scott-Blair elements, for which the constitutive equation includes a non-integer derivative ^[40]^[41]. At the turn of the 20th century, many definitions of fractional derivatives appeared, given by Liouville, Riemann, Grunwald and Letnikov. Currently, one of the most commonly used definitions of the fractional derivative is the Caputo derivative ^[42]. It can be proved that fractional models using a limited number of parameters make it possible to describe the behavior of VE materials at various frequencies, excitation amplitudes, and temperatures with acceptable accuracy ^[43]^[44]. The constitutive equation for such a model can be derived from Equation (1) by adopting the appropriate orders of derivatives smaller than unity (i.e.,

0 < m < 1

or/and

0 < n < 1

In the case of more complex models, it is also desirable to establish a relationship between the mechanical performance and the micro-configurations of the VE material, since changes in the rheological properties of the VE materials are attributed to a change in the microstructure ^[8]^[45]. It is proved that the higher-order fractional derivative model modified with the theory of internal variables and the principle of temperature–frequency equivalence is sufficiently accurate in describing the dynamic behavior of VE materials with varying frequencies and displacement amplitudes [44]. Non-linear models are created when it is assumed that the resistance force depends on the velocity and amplitude of deformation ^[46].

The VE properties are exhibited by various polymeric materials, such as adhesives, elastomers, and rubber. In order to accurately describe the dynamic behavior of a real VE material, it is essential to select a proper rheological model and correctly identify its parameters. Usually, the identification of model parameters requires a series of appropriate and relevant experiments and then, via a proper mathematical description of the physical behavior in the test, the results of the experiments are fitted to the mathematical model ^[47]. There are many methods for evaluating the performance of VE damping materials, which can be grouped in different ways.

In the context of the type of experimental tests, researchers can distinguish uniaxial tests ^[48], shear dynamic modulus tests ^[49], creep tests, stress relaxation tests ^[50]^[51], and beam bending tests ^[52]. All these tests can be dynamic ^[53] or pseudo-static, and they typically involve the measurement and acquisition of time histories of forces and displacements, which are then processed numerically ^[54].

In the case of static experiments, creep data are usually only available and the identification scheme is used to determine the parameters of the retardation function from the creep data ^[55]. The retardation function can then be transformed into a relaxation function. The relaxation experiment can be simulated by forcing a strain in the material and measuring the stress generated ^[51]. Studying the creep and the relaxation curves of materials is an effective method for dynamic testing at low frequencies, as the material needs time to respond to excitation ^[35].

In the vast majority of cases, experimental data are obtained by Dynamic Mechanical Analysis (DMA) ^[48]^[49]. DMA involves forcing the material to oscillate at a certain frequency and measuring its strain and stress beyond the resonant frequencies of the test stand. By varying the frequency, a transfer function can be built between the stress and strain over its wide range. This type of test is most suitable to acquire information on the frequency-dependent behavior ^[35].

With more advanced measurement technologies such as Digital Image Correlation (DIC) and Digital Volume Correlation (DVC), it is possible to obtain local information contained in full-field displacement/deformation data ^[56]. The use of DIC measurements in dynamic experimental tests can be subject to quality problems such as loss of grid points during loading, inaccessible measurements close to the boundary and non-Gaussian noise.

Depending on how the experimental data are processed, identification methods can be divided into two categories—direct and inverse identification methods ^[57]. In the direct methods, experimental dynamic data can be converted directly to dynamic stress–strain data or, equivalently, to the dynamic modulus at a specified frequency or strain rate ^[48]. The direct methods are not suitable for measuring dynamic mechanical properties of adhesives at lap joints with adherents because it is very difficult to distinguish between the elastic effects of the adherents and the adhesives ^[57].

In the category of inverse methods for identifying properties of VE materials, an inverse problem solving is used. For example, methods based on updating a FE model can be used. A numerical model of a structure with VE material is created. Then the parameters of the adopted material model are adjusted so that the response of the real structure measured in the experiment coincides with the results obtained from the finite element simulation ^[58]. Differences between measured and calculated values can be minimized using a gradient-based optimization algorithm to estimate the true values of the VE material model parameters ^[57]^[59].

The majority of identification cases are based on a cantilever beam specimen, where only damping of the VE material is included in the analytical model, whereas damping of the clamped specimen and air damping are usually ignored ^[60]. The results of some analyses show that the loss factor of VE materials would be overestimated if only material damping were included in the analysis model ^[61].

In the context of the fitting methods, stochastic techniques ^[62], evolution strategies ^[1]^[63] and optimization procedures ^[55]^[58]^[64]^[65] can be considered. Although no gradient information is needed in most of these methods, their performance is poor ^[47]. In addition, the process of parameter identification is an inverse problem that is determinate and it can be ill-conditioned due to noise present in the experimental data ^[1]. The choice of testing and fitting method also depends on the number of parameters present in the model that must be identified. Direct identification from time-domain or frequency-domain data is generally a difficult task, especially when more sophisticated models are required to achieve sufficient accuracy in relatively broad domains ^[66]. Some approaches to overcome these problems, illustrated by four identification methods, are described in ^[55].

When the number of model parameters is small, such as in the classical Kelvin or Maxwell models, appropriate algebraic operations can lead to formulae that determine the model parameters directly from the experiment results ^[67].

The hysteretic model allows the definition of a stress–strain or a load–displacement relationship using a closed-form expression that does not require any iterative algorithm to fully characterize the response ^[68]. The constitutive parameters represent physical properties that can be directly related to quantities deduced from experimental data ^[65].

Stochastic identification techniques have an advantage over deterministic methods in their ability to account for uncertainty associated with established models, which can be caused by varying material properties, as well as their spatial distribution, measurement or modeling errors and insufficient information available ^[62].

The Ant Colony Optimization algorithm can be used to solve the inverse problem of identifying unknown constitutive parameters in homogeneous/regionally inhomogeneous fractional VE fields ^[63].

Very recently, a computational homogenization framework for VE composites within the framework of non-ordinary state-based peridynamic theory was presented in ^[69]. The proposed framework was used to calculate the effective properties in both time and frequency domains of two VE matrix-inclusion composite systems—one with an elastic inclusion and VE matrix, and the other one with VE inclusion and an elastic matrix.

References

Lewandowski, R.; Słowik, M.; Przychodzki, M. Parameters identification of fractional models of viscoelastic dampers and fluids. Struc. Eng. Mech. 2017, 63, 181–193.
Spencer, B.F.; Nagarajaiah, S. State of the art of structural control. J. Struct. Eng. 2003, 129, 845–856.
Housner, G.W.; Bergmann, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971.
Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley: Chichester, UK; New York, NY, USA, 1997.
Eshaghi, M.; Sedaghati, R.; Rakheja, S. Dynamic characteristics and control of magnetorheological/electrorheological sandwich structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2003–2037.
Osial, M.; Pregowska, A.; Warczak, M.; Giersig, M. Magnetorheological fluids: A concise review of composition, physicochemical properties, and models. J. Intell. Mater. Syst. Struct. 2023, 34, 1045389X231157357.
Jones, D.I.G. Handbook of Viscoelastic Vibration Damping; Wiley: New York, NY, USA, 2001.
Shu, Z.; You, R.; Zhou, Y. Viscoelastic materials for structural dampers: A review. Constr. Build. Mater. 2022, 342, 127955.
Shu, Z.; Ning, B.; Li, S.; Li, Z.; Gan, Z.; Xie, Y. Experimental and numerical investigations of replaceable moment-resisting viscoelastic damper for steel frames. J. Constr. Steel Res. 2020, 170, 106100.
De Cazenove, J.; Rade, D.A.; de Lima, A.M.G.; Araujo, C.A. A numerical and experimental investigation on self-heating effects in viscoelastic dampers. Mech. Sys. Sig. Proc. 2012, 27, 433–445.
Chakraborty, B.C.; Ratna, D. Polymers for Vibration Damping Applications; Elsevier: Cambridge, MA, USA, 2020.
Shedbale, N.; Muley, P.V. Review on Viscoelastic Materials used in Viscoelastic Dampers. Int. Res. J. Eng. Technol. 2017, 4, 7.
Chen, Y.; Chen, C.; Ma, Q.; Jang, H.; Wan, Z. Study on mechanical properties of high damping viscoelastic dampers. Adv. Struct. Eng. 2019, 22, 2925–2936.
Wu, C.; Otani, Y.; Namiki, N.; Emi, H.; Nitta, K. Phase modification of acrylate rubber/chlorinated polypropylene blends by a hindered phenol compound. J. Polym. 2001, 33, 322–329.
Xu, Z.D.; Liao, Y.X.; Ge, T.; Xu, C. Experimental and theoretical study on viscoelastic dampers with different matrix rubbers. J. Eng. Mech. 2016, 142, 04016051.
Xu, Z.D.; Ge, T.; Liu, J. Experimental and theoretical study of high-energy dissipation-viscoelastic dampers based on acrylate-rubber matrix. J. Eng. Mech. 2020, 146, 04020057.
Xu, Z.D.; Yang, Y.; Zhu, Y.N.; Ge, T. Experimental study and mathematical modeling of viscoelastic dampers with wider temperature range based on blended rubber matrix. J. Build. Eng. 2023, 70, 106414.
Ge, T.; Xu, Z.D.; Yuan, F.G. Development of viscoelastic damper based on NBR and organic small-molecule composites. J. Mater. Civ. Eng. 2022, 34, 04022192.
Ge, T.; Xu, Z.D.; Yuan, F.G. Predictive model of dynamic mechanical properties of VE damper based on acrylic rubber–graphene oxide composites considering aging damage. J. Aero. Eng. 2022, 35, 04021132.
Xu, Y.S.; Xu, Z.D.; Guo, Y.Q.; Ge, T.; Xu, C.; Huang, X. Theoretical and experimental study of viscoelastic damper based on fractional derivative approach and micromolecular structures. J. Vib. Acoust. 2019, 141, 031010.
Teh, T.W.; Tan, C.G.; Jumaat, M.Z. Feasibility evaluation of novel high-damping rubbers as energy-dissipation material under axial dynamic load for damper devices. Buildings 2022, 12, 1917.
He, Z.; Shi, F.; Lin, Z.; Zhang, C.; Zhou, Y.; Zhao, F. Experimental characterization on cyclic stability behavior of a high-damping viscoelastic damper. Constr. Build. Mater. 2023, 371, 130749.
Nakamura, Y.; Hanzawa, T.; Nomura, T.; Takada, T. Performance-based placement of manufactured viscoelastic dampers for design response spectrum. Front. Built Environ. 2016, 2, 10.
Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. In Theoretical Analyses, Computations, and Experiments of Multiscale Materials; Giorgio, I., Placidi, L., Barchiesi, E., Abali, B.E., Altenbach, H., Eds.; Springer: Cham, Switzerland, 2022; Volume 175.
Genovese, A.; Carputo, F.; Maiorano, A.; Timpone, F.; Farroni, F.; Sakhnevych, A. Study on the generalized formulations with the aim to reproduce the viscoelastic dynamic behavior of polymers. Appl. Sci. 2020, 10, 2321.
Vasques, C.M.A.; Moreira, R.A.S.; Rodrigues, J.D. Viscoelastic damping Technologies—Part I: Modeling and finite element implementation. J. Adv. Res. Mech. Eng. 2010, 1, 76–95.
Bland, D.R. The Theory of Linear Viscoelasticity; Pergamon Press: Oxford, UK, 1960.
Tschoegl, N.W. Representation of Linear Viscoelastic Behavior by Series-Parallel Models. In The Phenomenological Theory of Linear Viscoelastic Behavior; Springer: Berlin/Heidelberg, Germany, 1989.
Steinmann, P.; Runesson, K. The Catalogue of Computational Material Models: Basic Geometrically Linear Models in 1D; Springer: Cham, Switzerland, 2021.
Lin, C.-Y. Rethinking and researching the physical meaning of the standard linear solid model in viscoelasticity. Mech. Adv. Mater. Struct. 2023, 1–16, in print.
Park, S.W. Analytical modeling of viscoelastic dampers for structural and vibration control. Int. J. Solids Struct. 2001, 38, 8065–8092.
Burgers, J.M. First and Second Report on Viscosity and Plasticity; Academy of Sciences at Amsterdam: Amsterdam, NY, USA, 1935.
Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948.
Huang, C.; Gao, D.; Meng, T.; Yang, C. Investigation into Viscoelastic Properties of Fiber-Reinforced Asphalt Composite Concrete Based on the Burgers Model. Buildings 2023, 13, 449.
Renaud, F.; Dion, J.L.; Chevallier, G.; Tawfiq, I.; Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech. Syst. Signal Process. 2011, 25, 991–1010.
Lewandowski, R.; Bartkowiak, A.; Maciejewski, H. Dynamic analysis of frames with viscoelastic dampers: A comparison of damper models. Struct. Eng. Mech. 2012, 41, 113–137.
Ottosen, N.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, NY, USA, 2005.
Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped materials. AIAA J. 1983, 21, 741–748.
Rossikhin, Y.A.; Shitikova, M.V. A new method for solving dynamic problems of fractional derivative viscoelasticity. Int. J. Eng. Sci. 2001, 39, 149–176.
Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 2003, 265, 935–952.
Lewandowski, R.; Chorążyczewski, B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comp. Struct. 2010, 88, 1–17.
Caputo, M. Linear models of dissipation whose is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539.
Lewandowski, R.; Przychodzki, M. Approximate method for temperature-dependent characteristics of structures with viscoelastic dampers. Arch. Appl. Mech. 2018, 88, 1695–1711.
Xu, Y.; He, Q.; Guo, Y.-Q.; Huang, X.-H.; Dong, Y.-R.; Hu, Z.-W.; Kim, J. Experimental and theoretical investigation of viscoelastic damper by applying fractional derivative method and internal variable theory. Buildings 2023, 13, 239.
Tang, S.; Greene, M.S.; Liu, W.K. Two-scale mechanism-based theory of nonlinear viscoelasticity. J. Mech. Phys. Solids 2012, 60, 199–226.
Vasile, O.; Bugaru, M. A New Modeling Approach for Viscous Dampers Using an Extended Kelvin–Voigt Rheological Model Based on the Identification of the Constitutive Law’s Parameters. Computation 2023, 11, 3.
Ghobadi, E.; Shutov, A.; Steeb, H. Parameter Identification and Validation of Shape-Memory Polymers within the Framework of Finite Strain Viscoelasticity. Materials 2021, 14, 2049.
Zhang, L.H.; Yao, X.H.; Zang, S.G.; Han, Q. Temperature and strain rate dependent tensile behavior of a transparent polyurethane interlayer. Mater. Des. 2015, 65, 1181–1188.
Martinez-Agirre, M.; Illescas, S.; Elejabarrieta, M.J. Characterisation and modelling of prestrained viscoelastic films. Int. J. Adhes. Adhes. 2014, 50, 183–190.
Chen, T. Determining a Prony Series for a Viscoelastic Material from Time Varying Strain Data; Technical Report; NASA: Washington, DC, USA, 2000.
Rothermel, R.; Panfilenko, W.; Sharma, P.; Wald, A.; Schuster, T.; Jung, A.; Diebels, S. A method for determining the parameters in a rheological model for viscoelastic materials by minimizing Tikhonov functionals. Appl. Math. Sci. Eng. 2022, 30, 141–165.
Najib, M.F.; Nobari, A.S.; Nikbin, K. Modification and evaluation of a FRF-based model updating method for identification of viscoelastic constitutive models for a nonlinear polyurethane adhesive in a bonded joint. Int. J. Adhes. Adhes. 2017, 74, 181–193.
Pawlak, Z.M.; Denisiewicz, A. Identification of the fractional Zener model parameters for a viscoelastic material over a wide range of frequencies and temperatures. Materials 2021, 14, 7024.
Vasques, C.M.A.; Moreira, R.A.S.; Rodrigues, J. Viscoelastic damping technologies—Part II: Experimental identification procedure and validation. J. Adv. Res. Mech. Eng. 2010, 1, 96–110.
Gerlach, S.; Matzenmiller, A. Comparison of numerical methods for identification of viscoelastic line spectra from static test data. Int. J. Numer. Meth. Eng. 2005, 63, 428–454.
Marino, E.; Flaschel, M.; Kumar, S.; de Lorenzis, L. Automated identification of linear viscoelastic constitutive laws with EUCLID. arXiv 2022, arXiv:2212.10969.
Najib, M.F.; Nobari, A.S. Nonlinear viscoelastic constitutive model identification for a polyurethane adhesive in a bonded joint using structural dynamic model updating. Mech. Mater. 2016, 100, 72–85.
Kim, S.-Y.; Lee, D. Identification of fractional-derivative-model parameters of viscoelastic materials from measured FRFs. J. Sound Vib. 2009, 324, 570–586.
Naraghi, T.; Nobari, A.S. Identification of the dynamic characteristics of a viscoelastic, nonlinear adhesive joint. J. Sound Vib. 2015, 352, 92–102.
Sun, W.; Wang, Z.; Liu, R.; Yan, X. Inverse Identification of the frequency-dependent mechanical parameters of a viscoelastic core layer based on the vibration response. Appl. Sci. 2017, 7, 455.
Sun, W.; Wang, Z.; Yan, X.; Zhu, M. Inverse identification of the frequency-dependent mechanical parameters of viscoelastic materials based on the measured FRFs. Mech. Syst. Signal Process. 2018, 98, 816–833.
Mehrez, L.; Kassem, E.; Masad, E.; Little, D. Stochastic Identification of Linear-Viscoelastic Models of Aged and Unaged Asphalt Mixtures. J. Mater. Civ. Eng. 2015, 27, 04014149.
Xiao, Z.; Haitian, Y.; Yiqian, H. Identification of constitutive parameters for fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 311–322.
Deng, R.; Davies, P.; Bajaj, A.K. Flexible polyurethane foam modelling and identification of viscoelastic parameters for automotive seating applications. J. Vib. Acoust. 2003, 262, 391–417.
Sessa, S.; Vaiana, N.; Paradiso, M.; Rosati, L. An inverse identification strategy for the mechanical parameters of a phenomenological hysteretic constitutive model. Mech. Syst. Signal Process. 2020, 139, 106622.
Grosso, P.; de Felice, A.; Sorrentino, S. A method for the experimental identification of equivalent viscoelastic models from vibration of thin plates. Mech. Syst. Signal Process. 2021, 153, 107527.
Lewandowski, R.; Chorążyczewski, B.; Wasilewicz, P. Evaluation of parameters of viscous fluid and viscoelastic dampers. Vib. Phys. Syst. 2006, 22, 223–228.
Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings. Compos. Struct. 2019, 211, 196–212.
Galadima, Y.K.; Oterkus, S.; Oterkus, E.; Amin, I.; El-Aassar, A.-H.; Shawky, H. A nonlocal method to compute effective properties of viscoelastic composite materials based on peridynamic computational homogenization theory. Compos. Struct. 2023, 319, 117147.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Civil

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Roman Lewandowski

Przemysław Litewka

Magdalena Łasecka-Plura

Zdzisław M. Pawlak

View Times: 864

Update Date: 09 Oct 2023

Table of Contents

Video Upload Options

Confirm

1. General Characteristics of Classical and New Viscoelastic Materials Used in Dampers and Layers

2. Models of Viscoelastic Materials and Identification of Theirs Parameters

References