Quantum-Resistant Blockchain System

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Joel Marion Marceline	--	2500	2023-09-20 03:58:59	\|
2	layout & references	Sirius Huang	Meta information modification	2500	2023-09-20 05:24:32	\|

This entry is adapted from the peer-reviewed paper 10.3390/math11183947

Blockchain transactions are decentralized, secure, and transparent, and they have altered industries. However, the emergence of quantum computing presents a severe security risk to the traditional encryption algorithms used in blockchain. Post-quantum signatures are required to preserve integrity and reliability. Furthermore, combining the InterPlanetary File System (IPFS) with blockchain provides a long-term strategy for data storage and sharing.

blockchain blockchain security cryptography quantum computing

1. Introduction

Blockchain transactions that are transparent, safe, and decentralized have changed entire sectors. Two basic strategies—quantum-secured blockchain and quantum-resistant blockchain—have been employed by researchers to protect blockchain in recent years from future quantum computer attacks. Digital signatures derived from quantum-resistant algorithms are used in quantum-resistant blockchain, although their practical applications are still limited, and the problem of long public keys still exists. Numerous industries have adopted blockchain technology, and almost 3000 virtual currencies, including well-known ones like Ethereum ^[1], Ripple, and Tether, use it for cross-border transactions.

The family of post-quantum algorithms with the highest efficacy in countering quantum attacks, which have garnered a lot of attention recently, is lattice cryptography. A few signature techniques based on lattice cryptography have been proposed in references ^[2]^[3]^[4]. These approaches aim to enhance transaction handling within blockchain systems, yet they prove ineffective for blockchain technologies operating in computationally intricate environments. Gao et.al. unveiled a blockchain-compatible double signing method ^[3]. The scheme’s security is solely predicated on the SIS assumption. Li et.al. created a technique for digital signatures using the bonsai trees technology ^[4]. Its security is established within the framework of the random oracle model. The author in ^[5] explores how blockchain technology is being used in smart cities and suggests a quantum-resistant blockchain platform built upon lattice cryptography. The paper ^[6] analyzes the most significant cryptocurrencies in the context of quantum risks, ranking them by market capitalization (MC). The author suggests a blockchain design for the Internet of Things (IoT) using the NTRU lattice, along with a cryptographic security validation for the system, in order to build a highly effective post-quantum blockchain infrastructure.

There are no recent data breaches or security breaches in the domain of blockchain using quantum computers, but there are some potential vulnerabilities due to the development of quantum computing, which highlights the urgency for introducing quantum-resistant algorithms. Demonstrations of quantum algorithms like Shor’s have showcased their potential to compromise widely used encryption techniques, placing data security at risk. Additionally, there is a concern regarding historical data encrypted using vulnerable methods, as they could be exposed in the future, posing potential breaches. Quantum computing’s ability to intercept and decrypt secure communications has significant implications for national security. Furthermore, blockchain technology, which relies on public key cryptography for its decentralized trust model, is particularly susceptible to quantum attacks that could expose private keys from public ones. Notably, a recent study reveals that a substantial portion of cryptocurrency holdings, including 25% of Bitcoin and 65% of ether, resides in addresses with publicly known public keys, raising concerns about their vulnerability to theft by powerful quantum computers. To mitigate these risks, it is imperative to expedite the development and adoption of quantum-resistant cryptographic solutions to ensure the continued security of digital systems and assets.

2. Blockchain Basics and IPFS

2.1. Blockchain-Enabled Systems

A technological infrastructure that uses blockchain technology to offer decentralized, open-source, and safe solutions for diverse applications is referred to as a blockchain-enabled system depicted in Figure 1.

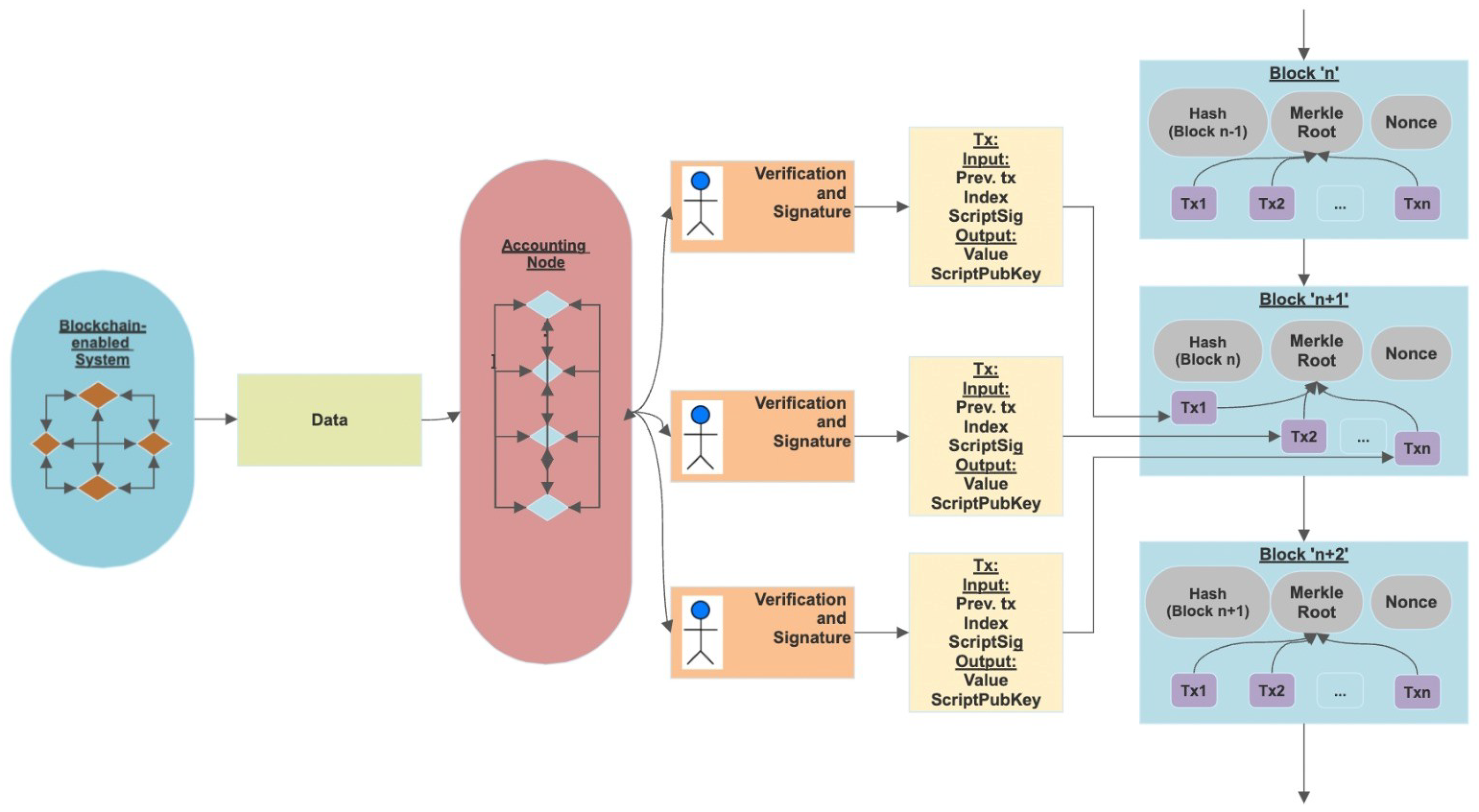
Figure 1. Representation of a blockchain-enabled system.

At its foundation, blockchain is a decentralized record keeping system that holds transactional data via an unchangeable and impenetrable method. By incorporating blockchain into many systems, it is possible to improve their effectiveness, reliability, and data integrity, giving them distinct advantages over classic centralized systems. Here are some essential traits and illustrations of systems that utilize blockchain technology:

Decentralization: blockchain removes the necessity for a central governing entity or middleman by operating within a decentralized network of interconnected nodes. By ensuring that no single entity controls the entire system, decentralization increases resilience and lowers the possibility of single points of failure.
Transparency and immutability: every transaction recorded on the blockchain is openly accessible to the public and is publicly viewable. A transaction becomes immutable once it is added to the blockchain, which means it cannot be changed or removed without network consent.
Security and data integrity: transactions are securely recorded and verified using cryptographic methods in blockchain technology. Any attempt to tamper with the data would require changing every transaction in the chain of blocks because each transaction is linked to the one before it.

2.2. Blockchain Security

Blockchain systems need to be secure in order to guard against fraud, tampering, and unauthorized access. This section explores key cryptographic techniques enhancing blockchain security.

Digital signatures: a crucial cryptographic tool utilized in blockchain technology is the digital signature. A private key and a public key are the two types of cryptographic keys that each member of the blockchain network has. The matching public key is made available to others in order to validate the legitimacy of the signatures, while the private key is kept secret and utilized to create digital signatures. Digital signatures demonstrate that a transaction has been approved by the holder of the private key, demonstrating the validity and authorization of transactions on the blockchain.
Hash functions: also known as message digests or hash codes. Hash functions are cryptographic techniques that transform data of any size into fixed-length, singular character strings. Each block in the blockchain contains the data from the preceding block’s hash value, resulting in a chain of blocks that are connected by their hashes. The blockchain’s immutability is ensured by this chaining method. It is simple to spot tampering because any alteration to the data within a block will result in a different hash value.
Merkle trees: Merkle trees are binary trees, also known as known as hash trees, that make it possible to verify huge datasets of data efficiently. Merkle trees are used in blockchain to arrange and compile the transactions contained in a block. Participants can quickly confirm the existence and integrity of particular transactions within a block without having to process all of the individual transactions thanks to the Merkle tree’s root hash, which is included in the block header.
Public key infrastructure (PKI): public key infrastructure encompasses a series of protocols and processes responsible for handling the generation, dispersion, and invalidation of digital certificates and public keys. In the blockchain context, PKI enables participants in the blockchain to validate each other’s public keys and confirm the validity of transactions by enabling them to authenticate each other’s public keys.
Consensus methods: for transaction authentication and the addition of new blocks in a blockchain, proof-of-work (PoW) and proof-of-stake (PoS) consensus mechanisms employ hash functions. This guarantees that only valid transactions are added.
Quantum-resistant cryptography: as quantum computing advances, established cryptographic techniques employed in blockchain, such RSA and ECC, are at risk of being compromised. Adopting quantum-resistant algorithms is essential to protect blockchain security from quantum threats in the future.

Some actual threats to blockchain technology are double spending, Sybil attacks, smart contract vulnerabilities, privacy concerns, key management, distributed denial of service (DDoS) attacks, and transaction malleability.

It is worth noting that, while quantum-resistant algorithms address the threat of quantum computing, they may not directly solve the other threats listed above. The other threats are typically mitigated through various cryptographic and non-cryptographic techniques. However, quantum-resistant cryptography plays a crucial role in ensuring the long-term security of blockchain networks in the face of quantum advancements.

2.3. InterPlanetary File System

The InterPlanetary File System (IPFS) revolutionizes online file storage and sharing by establishing a permanent and decentralized method. The IPFS’s primary objective is to offer a distributed file system that guarantees files that may be accessed from various places, removing the possibility of data loss due to server outages or shutdowns. The IPFS enables effective content retrieval and verification over the network by dividing files into smaller portions and giving them distinct cryptographic hashes. This cutting-edge technology has a number of benefits, including improved security, privacy, and user control. Without relying on a centralized authority, users can safely transfer files, lowering the possibility of censorship or unauthorized access to private information. Additionally, the IPFS is perfect for long-term information preservation because of its decentralized design, which permits files to endure forever. With regard to blockchain applications, the IPFS is used to store massive data, such as public keys and signatures, while the blockchain itself just stores the corresponding hash values. By doing this, the storage requirements of the blockchain are drastically decreased, resulting in more scalable and effective blockchain networks.

3. Quantum Computing’s Effects on Cryptosystems and the Need for Post-Quantum Cryptosystems

3.1. Quantum Computing

The cutting-edge discipline of computing known as quantum computing uses the concepts of quantum physics to process and modify data. Quantum computers employ quantum bits, also known as qubits, which can exist in several states at once due to the phenomenon known as superposition. This is in contrast to classical computers, which use bits to encode data as either 0 or 1.

Using quantum Fourier transform ^[7] to solve problems related to integer factorization and discrete logarithms can be exponentially sped up using Shor’s approach ^[8]. The searching problem can be quadratically sped up using Grover’s algorithm ^[9]. It offers a significant speed advantage over the conventional brute force approach, which takes

O (N)

time in classical attacks. This method can find the original input corresponding to a function’s output in approximately

O (\sqrt{N})

time. Many widely used encryption systems rely on these intricate mathematical challenges. However, quantum computers are expected to solve these problems within a bounded polynomial time.

The extent to which these quantum benefits can be developed and the duration of the feasibility gap between classical and quantum models are also unknown ^[10]. The question of whether it is possible to create a large-scale quantum computer is complex and contentious. Many researchers now think that enormous quantum computers are just a very difficult engineering problem, although in the past it was less obvious whether they were a physical reality.

In the next 20 years or so, according to any scientists who still make such predictions ^[11], powerful quantum computers will be developed that will be able to break all of the current core public key infrastructures quickly. It will take much work to enable a seamless and stable transition from the newest widely used cryptosystems to their counterparts that can withstand quantum computing. Regardless of whether we are able to predict with accuracy when the era of quantum computing will begin, we must continue building more secure communication channels that, for instance, might revolutionize the field of cryptography.

3.2. Post-Quantum Cryptosystems

Due to their reliance on mathematical problems that can be solved effectively by quantum computers, existing cryptographic systems like RSA and ECC may become vulnerable as quantum computing technology develops. A cryptographic system created on alternative mathematical structures and algorithms to survive attacks from quantum computers is known as a post-quantum cryptosystem. With the advent of potent quantum computers, these new cryptographic techniques seek to increase security and guarantee the ongoing preservation of critical data. Post-quantum signatures are known as quantum-resistant signatures or quantum-safe signatures. In the age of quantum computing, post-quantum signature systems are appropriate for secure communications and digital identity verification since they are made to be capable of withstanding assaults from both conventional and quantum computers. Post-quantum signature systems will aid in ensuring the long-term security of digital communications and safeguarding sensitive data from potential quantum attacks once they are widely adopted and put into use. In order to provide a collection of safe post-quantum cryptography algorithms, standardization efforts are still being made. To guarantee these algorithms’ efficacy and compatibility, organizations like the National Institute of Standards and Technology (NIST) are driving the technique of soliciting, assessing, and standardizing them.

Post-quantum signature schemes can be classified into five categories: hash-based, lattice-based, code-based, multivariate polynomial-based, and super-singular isogeny-based schemes.

3.2.1. Code-Based Cryptosystem

Code-based cryptography relies on the difficulty of decoding specific structured linear error-correcting codes. Daniel J. Bernstein proposed Classic McEliece, which is a potential post-quantum public key cryptographic system based on error-correcting codes under consideration by the NIST for global standardisation, in 2017 ^[12]^[13]^[14]. In the McEliece concept, a public key is formed through a combination of the Goppa code and a linear transformation. To encrypt a message, the sender introduces a set level of random noise to the message ^[15]. Without knowing how to factor in the public key, recovering the message is a computationally difficult job for the attacker. Several code-based cryptographic methods exist, and, among them, certain ones could potentially provide security against quantum attacks: Classic McEliece, BIKE, and HQC.

3.2.2. Hash-Based Cryptosystem

The cryptographic secure hash function used in hash-based signatures is created to exhibit security properties, like being hard to reverse, resistant to finding original inputs, immune to generating similar outputs for different inputs, and robust against collision attacks. Hash-based signature schemes are classified as stateless or stateful based on their implementation approach. They can also be categorized as a one-time signature (OTS), few-time signature (FTS), multi-time signature (MTS), and hierarchical signature (HS). These classifications depend on factors such as how keys are generated, how signatures are generated, and other parameters used in their construction.

S P H I N C S^{+}

is a hash-based quantum-safe cryptographic algorithm. It is a signature system with no state and an improved version of SPHINCS, designed to reduce signature size ^[13].

3.2.3. Lattice-Based Cryptosystems

These cryptographic techniques are constructed using lattices, which are sets of points arranged periodically in multi-dimensional spaces. To find the smallest non-zero point within a lattice, a complex problem known as the shortest vector problem (SVP) is utilized. This problem, which is difficult to solve and falls under the NP-hard category, forms the foundation of security in lattice-based systems. Additional challenges related to lattices, such as the closest vector problem (CVP) and the shortest independent vectors problem (SIVP), as mentioned by ^[16], are currently beyond the capabilities of quantum computers. The algorithm’s implementation is relatively efficient, and it provides worst-case hardness-based security proofs that are extremely strong. The quantum-resistant algorithms based on the lattice are CRYSTALS-KYBER, SABER, NTRU, FrodoKEM, NTRU Prime CRYSTALS-Dilithium, and FALCON.

3.2.4. Multivariate-Based Cryptosystems

Multivariate system of equations have been demonstrated to be NP-complete or NP-hard, and multivariate-based techniques rely on this complexity ^[12]. Despite their resilience to quantum assaults, more research is required to increase their decryption speed, decrease their enormous key size, and lower their ciphertext overhead ^[17]. Rainbow and GeMSS are the potentially quantum-safe cryptographic techniques based on multivariate quadratic equations.

3.2.5. Super Singular Elliptic Curve Isogeny Cryptosystems

These are a novel approach that first appeared in the year 2000. To create public key cryptosystems, isogeny-based cryptography employs mappings between elliptic curves. Isogeny cryptography relies on the security of solving super singular isogeny problems. These problems involve finding the connection (isogeny mapping) between two super singular elliptic curves that have an equal count of points. In comparison with other post-quantum cryptography possibilities, the protocols based on isogeny need a very small key. SIKE is one of the isogeny cryptography family’s putative quantum-safe algorithms ^[18]^[19]^[20].

References

Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32.
Yin, W.; Wen, Q.; Li, W.; Zhang, H.; Jin, Z. An anti-quantum transaction authentication approach in blockchain. IEEE Access 2018, 6, 5393–5401.
Gao, Y.L.; Chen, X.B.; Chen, Y.L.; Sun, Y.; Niu, X.X.; Yang, Y.X. A secure cryptocurrency scheme based on post-quantum blockchain. IEEE Access 2018, 6, 27205–27213.
Li, C.Y.; Chen, X.B.; Chen, Y.L.; Hou, Y.Y.; Li, J. A new lattice-based signature scheme in post-quantum blockchain network. IEEE Access 2018, 7, 2026–2033.
Zhang, P.; Wang, L.; Wang, W.; Fu, K.; Wang, J. A blockchain system based on quantum-resistant digital signature. Secur. Commun. Netw. 2021, 2021, 6671648.
Ciulei, A.T.; Crețu, M.C.; Simion, E. Preparation for post-quantum era: A survey about blockchain schemes from a post-quantum perspective. Cryptol. ePrint Archive 2022. Available online: https://eprint.iacr.org/2022/026 (accessed on 16 March 2023).
Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information. Phys. Today 2001, 54, 60.
Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332.
Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219.
Chen, L.; Chen, L.; Jordan, S.; Liu, Y.K.; Moody, D.; Peralta, R.; Perlner, R.; Smith-Tone, D. Report on Post-Quantum Cryptography; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016; Volume 12.
Mosca, M. Cybersecurity in an era with quantum computers: Will we be ready? IEEE Secur. Priv. 2018, 16, 38–41.
Bernstein, D.J. Introduction to post-quantum cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14.
Bernstein, D.J.; Hülsing, A.; Kölbl, S.; Niederhagen, R.; Rijneveld, J.; Schwabe, P. The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 2129–2146.
Singh, H. Code based cryptography: Classic mceliece. arXiv 2019, arXiv:1907.12754.
McEliece, R.J. A public-key cryptosystem based on algebraic. Coding Thv. 1978, 4244, 114–116.
Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108.
Petzoldt, A.; Bulygin, S.; Buchmann, J. Selecting parameters for the rainbow signature scheme. In Proceedings of the Post-Quantum Cryptography: Proceedings of the Third International Workshop, PQCrypto 2010, Darmstadt, Germany, 25–28 May 2010; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2010; pp. 218–240.
Costello, C. Supersingular isogeny key exchange for beginners. In Proceedings of the Selected Areas in Cryptography, SAC 2019: 26th International Conference, Waterloo, ON, Canada, 12–16 August 2019; Revised Selected Papers 26. Springer: Berlin/Heidelberg, Germany, 2020; pp. 21–50.
De Feo, L. Mathematics of isogeny based cryptography. arXiv 2017, arXiv:1711.04062.
Taraskin, O.; Soukharev, V.; Jao, D.; LeGrow, J.T. Towards isogeny-based password-authenticated key establishment. J. Math. Cryptol. 2020, 15, 18–30.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Information Systems

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

P. Thanalakshmi

A. Rishikhesh

Joel Marion Marceline

Gyanendra Prasad Joshi

Woong Cho

View Times: 441

Update Date: 20 Sep 2023

Table of Contents

Video Upload Options

Confirm