Theoretical Consideration of Molecular Helicenes and Their Properties

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Robert Evarestov	--	3462	2023-09-12 19:20:34	\|
2	references update	Fanny Huang	-3 word(s)	3459	2023-09-14 05:49:47	\|

This entry is adapted from the peer-reviewed paper 10.3390/nano13162295

Some theoretical studies of properties of helicenes are considered. It was shown that helicenes are promising molecules for use as components of various nanodevices, due to the continuous π-system having a helical topology. Peripheral modifications of the edges make it possible to change the properties of helicenes over a wide range. The transition to polymeric helicenes is also considered.

helicene

1. Introduction

Helical structures formed at the molecular level have attracted the attention of researchers for a long time. Many molecular structures in living organisms exist in the form of helices, in particular DNA and RNA molecules and various peptides. Such molecules are natural polymers. The successive development of methods of polymer organic chemistry has led to the possibility of the synthesis of artificial stereoregular polymers, the threads of which are also ordered in a spiral manner (helical polymers) ^[1]^[2]^[3]. The spiral topology opens up great opportunities for various technological applications regarding helical polymers. In particular, the circularly polarized luminescence (CPL) of cis-cisoid polyene-based polymers ^[4], the magneto-optical properties of helical poly-3-(alkylsulfone)thiophene ^[5], various stimuli-responsive devices as sensors ^[6], asymmetric catalysis and chiral recognition ^[2], and chirality-induced spin selectivity (CISS) ^[7] should be mentioned.

The development of experimental methods for the synthesis of nanostructures that are much more extended in one dimension than in the other two (for brevity, researchers call such objects one-dimensional, 1D) made it possible to obtain nano objects of various morphologies and structures, including helical ones ^[8]. Among the most frequently used synthetic methods that allow for 1D helical objects to be obtained are the following: (i) the screw-dislocation-driven growth of 1D crystals ^[8] and (ii) various methods based on the addition of a chiral component to the reaction mixture (template-assisted synthesis) ^[9]. The 1D nanostructures with intrinsic chirality can be noted separately. The existence of such 1D crystals is due to the fact that the symmetry of the initial 3D crystals of these compounds is described by the Sohncke symmetry groups ^[10]. Among such structures, recently synthesized ultrathin tellurium nanorods can be mentioned ^[11].

Helical 1D nanostructures, here referred to as nanohelicenes ^[12], with both helical polymers and nanorods with intrinsic chirality can be considered. In molecular [n]helicenes, the number n denotes the number of ortho-fused benzene rings ^[13]. If n tends to infinity, then a polymeric [∞]helicene will be obtained, which can be considered as a ribbon infinitely turned along the helical axis (Figure 1). By considering [∞]helicene as the basic nanohelicene, it is possible to construct many modifications that will have different properties. At the same time, all nanohelicenes will have two main properties—a continuous π-system, and a helical topology.

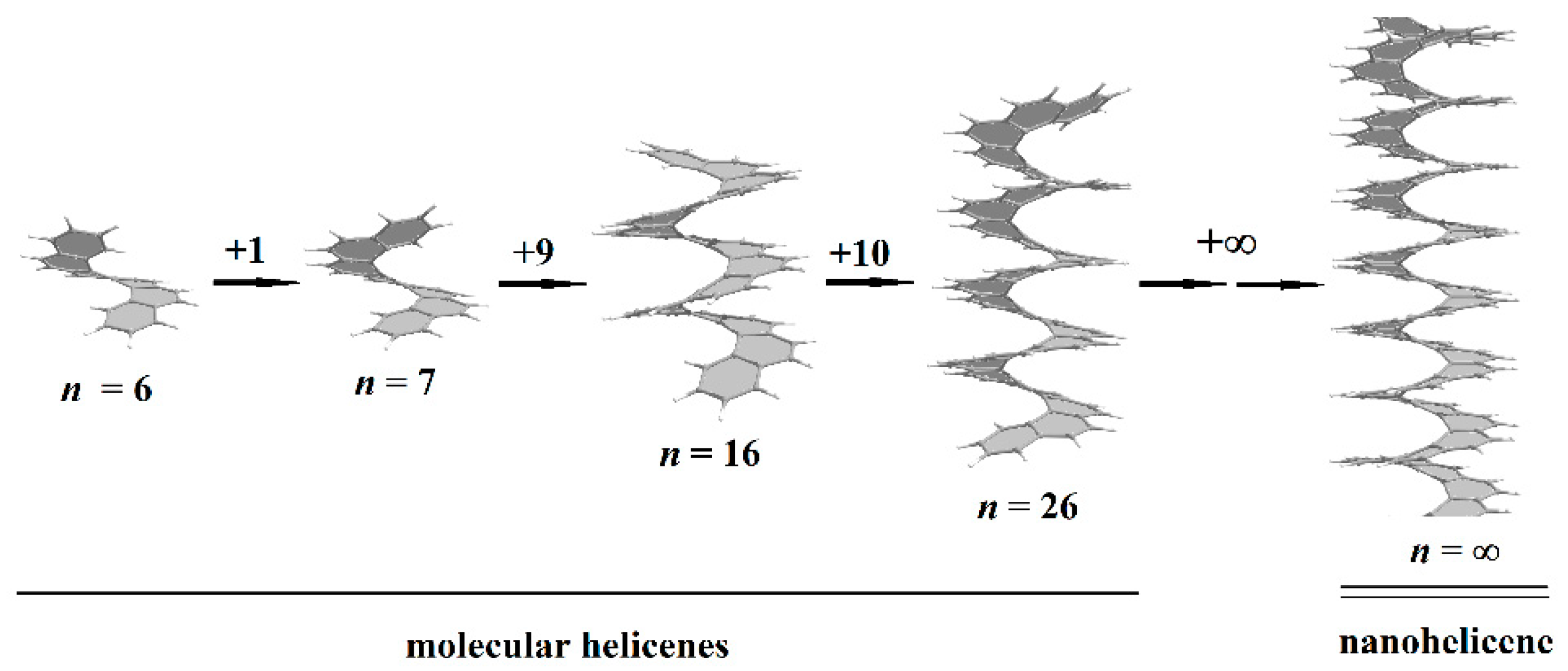
Figure 1. Molecular [n]helicenes and nanohelicene. From left to right: [6]helicene, [7]helicene, [16]helicene, [26]helicene, and [∞]helicene = nanohelicene. Gray and white spheres are carbon and hydrogen atoms, respectively.

Further, the consideration of nanohelicenes as “graphite” nanorods with a screw dislocation ^[14]^[15] makes it possible to understand these objects as structures formed by a graphene ribbon of a special morphology, which allows it to helically turn around a screw axis.

Therefore, other names are also used for nanohelicenes: “graphene spiral” ^[16], “graphene helicoid” ^[17], “helical graphene nanoribbon” ^[18], and “helical graphene” ^[19]. In addition, conventional graphene nanoribbons can be twisted into “helicoidal graphene nanoribbons” ^[20], which are qualitatively different from the objects considered here.

2. Theoretical Consideration of Molecular Helicenes and Their Properties

Molecular helicenes have a long story. In 1956, the [6]helicene was synthesized ^[21], which can be considered as one coil of the [∞]helicene. The synthesis of helicenes with two coils began in 1967 with the synthesis of the [7]helicene ^[22]. In 2015, the [14]helicene was obtained ^[23], i.e., helicene with three incomplete coils, and, to date, helicene with maximum n (Figure 1) remains to be obtained experimentally. It can be assumed that a further increase in n is a difficult synthetic problem, which is due to significant steric hindrance existing for inner atoms. However, there are some experimental data ^[24] that enable one to speculate on the presence of helicenes in interstellar space up to the [26]helicene (with more than four coils), which can be explained on the basis of the principles of minimum energy and polarizability (Figure 1) ^[25]^[26]^[27].

Thus, at the moment, the properties of helicenes with a further increase in n, and the approximation of properties to n → ∞ can only be estimated based on quantum chemical calculations. The first quantum chemical calculations (at the level of semi-empirical CNDO/S, PM3, and the HF method) of the helicenes appeared quite a long time ago and dealt with the structure of helicenes, racemization barriers, and chiroptical properties ^[28]^[29]^[30]. In ^[31], the effect of the distortion of the π-system due to twisting was theoretically investigated by comparing the energy characteristics of [n]helicenes and their planar counterparts, [n]phenacenes. The calculations were carried out at the level of HF/6-31G* and B3LYP/6-31G* at n = 6–10 and n = 16 and in the more powerful 6-311G** basis set for n = 6–10.

The dependence of the difference, ΔE, between the energies of helicenes and phenacenes with increasing n was considered ^[31]:

Δ E (n) = E ([n] helicene) - E ([n] phenacene)

The results show a linear increase in the ΔE between helicenes and phenacenes with increasing n. In other words, an increase in n does not lead to any stabilization of helicene. At n = 16 (largest experimentally synthesized helicene), the difference reaches 83.4 kcal/mol (the result of B3LYP/6-31G* calculations). This makes it possible to understand the observed difficulties in obtaining helicenes with a further increase in n.

The difference in magnetic susceptibilities between helicenes and phenacenes was also investigated in ^[31]. This quantity enables us to determine the aromaticity of the studied molecules. According to the data of ^[31], helical distortions in the π-system expectedly lead to a decrease in the aromaticity of helicenes in comparison with phenacenes. However, this decrease is not so large—the loss of aromaticity in helicenes is approximately 10–13% compared to phenacenes.

Similar results were obtained by the authors of ^[32], who performed DFT calculations using the functional B3LYP with the TZVP basis set and the empirical Grimme correction to account for the dispersion forces ^[33] and applying the conductor-like screening model (COSMO) ^[34] to take into account the solvent (acetonitrile). Incremental Gibbs free energies, ΔG_n, were obtained, which show the difference between the homodesmic addition of naphthalene (C₁₀H₈) to helicene or phenacene:

Δ G_{n} = G ([n]) + G (benzene) - G ([n - 1]) - G (naphthalene)

Here, G([n]) and G([n − 1]) are the Gibbs free energies of [n]helicene or [n]phenacene and [n − 1]helicene or [n − 1]phenacene, respectively. The ΔG_n reaches a constant value of ~10 kJ/mol at n ~ 6 for helicenes, which qualitatively corresponds to the result of ^[31] on inherent instability and explains the difficulty of the synthesis of helicenes with a large n. A similar result was obtained at the M06-2X/6-311+G(3d,p) level of calculations ^[35].

Researchers also note that the small difference between the aromaticity of helicenes and phenacenes noted earlier in ^[31] is confirmed by the results of subsequent works ^[32]^[35].

For the first time, the possibility of using helicene in terms of springs for application in nanotechnologies was discussed in ^[36]. From this point of view, at the level of the semi-empirical PM3 Hamiltonian, the force constants of axial tension for neutral helicenes and their cationic and anionic forms were estimated. Calculations were made for helicenes with n = 12 and 18, which corresponds to the number of coils of two and three, respectively. According to ^[36], the force constants are in the range 9.8–14.6 kcal·mol⁻¹·Å⁻² for small “springs” and approximately in the range 4.9–5.4 kcal·mol⁻¹·Å⁻² for large “springs”. The differences in hardness depend little on the electronic state of helicenes (i.e., neutral, cationic, or anionic states).

In ^[32], a somewhat larger value was obtained for [14]helicene, equal to 23.6 kcal·mol⁻¹·Å⁻². It can be assumed that the difference is due to a more accurate calculation method, which was carried out within the DFT (B3LYP functional) in the TZVP basis set, taking into account the solvent and dispersion corrections. A further theoretical study of the influence of the axial deformations of [∞]helicene and its non-hexagonal modifications on mechanical stability, deformability, and fracture processes was carried out in ^[37] at the PBE/PAW level of theory. It was found that the presence of pentagons or heptagons instead of hexagons had a significant influence on the mechanical properties, and some helicenes could achieve very large reversible tensile strains (more than 200%). The roughly estimated effective tensile strength of pristine [∞]helicene is equal to 117 GPa.

The authors of ^[32] also made an attempt to computationally evaluate the convergence of the physicochemical properties of [n]helicenes with increasing n. The results of TD DFT calculations of excitation energies ^[32] agree well with experiments and demonstrate the convergence of the results at n ~ 14. In particular, for [14]helicene, the calculated wavelength for the S₀ → S₁ vertical transition is 476 nm (2.60 eV).

The convergence of the gap between the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) was studied at the B3LYP/6-31G* computational level ^[38]. Calculations were carried out for helicenes and phenacenes (and their analogs with sulfur) with an n of up to 30 and under PBCs (periodic boundary conditions) in order to obtain the change in the electronic band gap of the structures with n → ∞. The data obtained for [14]helicene in ^[38] correlate with the results in ^[32], taking into account the fact that the HOMO–LUMO gap is only an upper estimate of the energies of the S₀ → S₁ vertical transition obtained by the TD DFT.

The obtained extrapolations are very close to the results of the calculations under PBCs (2.90 eV and 3.59 eV for [∞]helicene and [∞]phenacene, respectively ^[38]). The value 2.90 eV correlates with the 2.49 eV value obtained for [∞]helicene by the authors of earlier work ^[39].

Ref. ^[39] is the first work in which the infinite [∞]helicene was also considered (in the periodic model at the tight-binding level). In addition, researchers note that in ^[39], not only simple [∞]helicene but also its other topological variants (anthra-helicene and benzo-helicene) were considered for the first time. [∞]benzo-helicene has been shown to be potentially metallic, with a zero band gap, unlike simple [∞]helicene, which is a semiconductor.

The band structure of these two 1D structures shows that the [∞]benzo-helicene conduction band is “inside” the band gap of [∞]helicene, which allowed the authors of Ref. ^[39] to propose a variant of a quantum dot constructed as a hybrid of semi-conductor helicene and metallic benzo-helicene. The I/V characteristics (i.e., current-voltage) were calculated for finite size ^[21]benzo-helicene, [24]helicene, and their hybrid. As expected from the band structure, the I/V curve of the hybrid is similar to that of semiconductor helicene. This can also be understood in terms of the molecular orbitals (MO) of the hybrid. It can be seen from the figure that the MOs, which correspond to the energy levels within the band gap of the semiconductor part, will be localized on the metal part of the hybrid. If the voltage exceeds the band gap value of the semiconductor part, then the conductivity is restored, and MOs are delocalized throughout the hybrid. Hybrids that combine different types of helicenes have not been theoretically studied anywhere except in ^[39].

Researchers also note that in ^[39], for the first time, such issues as the Peierls distortion of metallic helicene were raised, and a decrease in the band gap with “expanding” helicene (i.e., a transition from simple helicene to anthra-helicene) was also shown. These issues were repeatedly analyzed in subsequent theoretical works on nanohelicenes.

In ^[40], the stability and properties of some other classes of helicenes were theoretically studied at the B3LYP/6-31G* level. Some ways for constructing a spiral from various combinations of hexagons, pentagons, and tetragons from carbon atoms were considered, including the “lateral-extending” of the helicene’s π-system, which is the object of study in subsequent theoretical works.

The presence of a continuous π-system and axial chirality makes helicenes and their derivatives promising for achieving non-linear optical (NLO) properties. At the level of the semi-empirical AM1 Hamiltonian, within the framework of the time-dependent Hartree-Fock (TD HF) theory, the change in the first hyperpolarizability (

\bar{β}

) and its projection on the dipole moment (

β_{∥}

) were theoretically studied with a successive increase in n (up to n = 19) for helicenes and their antiaromatic analogs, phenylenes ^[41]. It was found that

\bar{β}

increases monotonically with the size of the system. At the same time, in helicenes,

β_{∥}

is positive and presents quasi-periodic oscillations with the helix.

It was theoretically shown at the PBEPBE/6-31G(d,p) level that the modification of the helicene backbone by fusing the azulene element leads to a significant enhancement of the second-order NLO properties due to the polar charge distribution in the pentagon end (a component of azulene) ^[42]. NLO properties have also been shown to exhibit only slight changes under an external strain.

Further works in this area concerned third-order NLO properties, two-photon circular dichroism, and so on. A detailed review of the calculations and experiments on the NLO properties of helicenes and their derivatives is presented in a recent book ^[43].

Theoretical studies of electron transport through helicenes were the subject of works ^[44]^[45]^[46]^[47]^[48]. The common result for all the works mentioned is the conclusion about the presence of a strong dependence of conductivity and other properties on the applied mechanical stress. This is a fairly expected result based on the understanding of helicenes as molecular springs.

In particular, helicene-based molecular junctions constructed as (diaza)helicenes placed between two Au(111) electrodes were studied in ^[44]. Helicene compression leads to a significant increase in conductance, whereas stretching leads to a decrease. In the range of low voltages, conductance falls off linearly on a logarithmic scale as a function of strain. The thermopower shows a sign change, which implies a change in the transport mechanism of the junction. The dependence of the thermoelectric figure of merit (FOM), zT, on strain for increasing n values shows that the maximal values of FOM were obtained for the longest helicene. The maximal zT values can be as large as ~0.6, which far exceeds the values for currently known molecular junctions.

In ^[45], a wider tension-compression interval for [12]helicene was theoretically investigated, and the results on I/V behavior correlate with the results of ^[44] in the corresponding interval. However, the use of a wider interval made it possible to detect an increase in conductivity in the region of large stretches. Thus, current dependence on pitch has a U-shape. The first part of the curve (the distance between coils is less than 4 Å) corresponds to the transmission pathways between helicene coils (through space). The ascending part of the curve corresponds to a change in the conduction mechanism, and the conduction is due to transmission along the helicene ribbon (through bond).

At PBE/DZP computational level, the authors of ^[46] investigated the electronic transport properties of spiral-shaped molecules coupled to metal electrodes. Three molecules were composed of [7]helicene and two thiol-[7]helicenes with benzenethiolates on both sides. The data on local transmission pathways demonstrate that there is no spiral current flowing through [7]helicene, and the total current is only due to electron tunneling in the inter-layer. In the case of thiol-[7]helicenes, the electron distribution in frontier orbitals will change, and the spiral current will appear, which makes it possible to generate a magnetic field. The negative differential resistance behavior of I/V curves was also found in ^[46]. In other words, in a certain interval of bias voltage, the current decreases with bias increases.

A similar result about the absence of a helical current for helicenes was obtained in ^[47]. It was also shown in ^[48] that the conductivity of the oligomers of [n]benzo-helicene (see ^[39]) is significantly higher than that of conventional [n]helicenes. In the limit, this corresponds to the metallic conductivity of [∞]benzo-helicene that was shown in ^[39].

In addition to electrical conductivity studies, the theoretical calculations were also concerned with the potential application of helicene molecules to control spin transport. Such control has many advantages over conventional electronic transport and can potentially be used in nanodevices that are smaller and more robust than modern nanodevices. The use of helicene derivatives as a spin filter exhibiting the CISS effect was shown experimentally ^[49]. According to the general theory, the driving force behind CISS is spin-orbit interaction, SOC. Despite the fact that for carbon atoms, the SOC value is very small (about 6 meV), the CISS for these molecules can be significant ^[50], which opens up great opportunities for the use of organic chiral molecules, and in particular, helicenes.

The first theoretical consideration of spin-polarized electron transport in helicene was carried out in ^[51]. The [n]helicenes (n = 12, 16, 20, and 24) combined with semi-infinite graphene nanoribbons were considered. The spin polarization, P_s, is determined through spin-up G_↑ and spin-down G_↓ conductance, according to Equation (3):

P_{s} = (G_{↑} - G_{↓}) / (G_{↑} + G_{↓})

Using the tight-binding Hamiltonian with the addition of the SOC Hamiltonian, it was shown that the P_s of [20]helicene could reach 27%, which is comparable to the experimentally found values in ^[49]. Interestingly, P_s exhibits significant oscillations by varying the Fermi energy, E, because of quantum interference effects. In addition, the influence of axial deformations on P_s was studied. Axial deformations significantly change the overall shape of the P_s(E) curve; however, the oscillation behavior remains in the energy spectrum regardless of the applied mechanical stress, and the spin filtration efficiency remains quite large. The P_s(E) curves for other helicenes differ significantly in terms of peak heights and their location, but the overall picture remains the same as in the case of [20]helicene.

Since the CISS effect relates primarily to excited electron states, it should be observed not only in the case of flowing current but also in the case of a photocurrent promoted by photo-excited electrons. In ^[52], an experimental and theoretical study of [7]helicene molecules adsorbed on metal surfaces (Cu(332), Ag(110), and Au(111)) was carried out. An excess of 6–8% of longitudinal spin polarization, P_Z, was demonstrated:

P_{Z} = \frac{I_{↑} - I_{↓}}{I_{↑} + I_{↓}} S_{eff}^{- 1}

Here, I_↑,↓ denotes the count rates in the two detectors, and S_eff is the effective Sherman function. It is important to note that circularly polarized UV/Vis light served as the source of spin polarization. Thus, the obtained experimental results connect two promising phenomena—CISS and CPL, which is possible in this case. In the computational part of Ref. ^[52], the DFT method was used to study the [7]helicene molecules adsorbed on different surfaces. Then, using the model Hamiltonian to calculate the CISS, P_Z was obtained for helicenes with different numbers of coils. The results showed a significant increase in P_Z for the system with the maximum number of coils (three in the case under study). Interestingly, the authors of ^[53] explored the CISS associated with inter-system crossing (ISC) in carbon-sulfur [n]helicenes. It has been suggested that the efficient ISC of these molecules might be beneficial for an efficient CISS.

Spin transport through helicenes bonded to a carbon zigzag-terminated nanoribbon was theoretically studied in ^[54]. Some peripheral modifications of helicene with one coil were considered, starting from the basic [6]helicene. The helicene periphery was successively expanded by adding from one to three carbon hexagons. The calculations were carried out at the DFT+NEGF (non-equilibrium Green function) level with the DZP basis set.

It was shown that in the case of basic helicene, both spin states on the central spiral moiety reveal transport via inter-layer tunneling without the generation of spiral current, which is similar to the results of ^[45]^[46]. Spin-polarized transport is present but is relatively small. However, modification by adding carbon hexagons resulted in a robust spin-polarized interaction, especially in the case of the appearance of trigonal sections. According to the Lieb theorem ^[55] (regarding the total spin of the Hubbard model in bipartite sublattices A and B), these parts have extra atoms that break the balance between the number of atoms in sublattices, i.e., N_A ≠ N_B. Consequently, the emergence of magnetism is induced by edge imbalance. Additionally, depending on the location of additional hexagons, helicene-based devices exhibit an on-off spin-polarization phenomenon, which manifests itself in the presence/absence of spin-splitting that is dependent on bias. Interestingly, the location of additional hexagons also affects the type of electron tunneling. In the case of trigonal modification, it was possible to redirect the current completely in a spiral, i.e., intra-layer tunneling is a major contribution to current, which is in contrast to the basic helicene case.

Despite the fact that the theoretical works considered mainly refer to molecular helicenes, the manifestation of many of the effects found can also be expected for nanohelicenes. Researchers especially note the importance of structural modification, which consists of the addition of carbon hexagons to the carbon skeleton of the initial [n]helicene. From the results of theoretical studies, it can be clearly seen that modification leads to a significant change in the optical, electronic, and magnetic properties, and taking into account the spring topology of helicenes makes such modifications extremely promising for creating corresponding opto-, electro-, and magneto-mechanical devices at the nano level.

References

Nakano, T.; Okamoto, Y. Synthetic Helical Polymers: Conformation and Function. Chem. Rev. 2001, 101, 4013–4038.
Yashima, E.; Maeda, K.; Iida, H.; Furusho, Y.; Nagai, K. Helical Polymers: Synthesis, Structures, and Functions. Chem. Rev. 2009, 109, 6102–6211.
Yashima, E.; Ousaka, N.; Taura, D.; Shimomura, K.; Ikai, T.; Maeda, K. Supramolecular Helical Systems: Helical Assemblies of Small Molecules, Foldamers, and Polymers with Chiral Amplification and Their Functions. Chem. Rev. 2016, 116, 13752–13990.
Wang, S.; Hu, D.; Guan, X.; Cai, S.; Shi, G.; Shuai, Z.; Zhang, J.; Peng, Q.; Wan, X. Brightening up Circularly Polarized Luminescence of Monosubstituted Polyacetylene by Conformation Control: Mechanism, Switching, and Sensing. Angew. Chem. Int. Ed. 2021, 60, 21918–21926.
Wang, P.; Jeon, I.; Lin, Z.; Peeks, M.D.; Savagatrup, S.; Kooi, S.E.; van Voorhis, T.; Swager, T.M. Insights into Magneto-Optics of Helical Conjugated Polymers. J. Am. Chem. Soc. 2018, 140, 6501–6508.
Huang, C.-B.; Ciesielski, A.; Samorì, P. Molecular Springs: Integration of Complex Dynamic Architectures into Functional Devices. Angew. Chem. Int. Ed. 2020, 59, 7319–7330.
Fransson, J. The Chiral Induced Spin Selectivity Effect What It Is, What It Is Not, and Why It Matters. Isr. J. Chem. 2022, 62, e2022000.
Ren, Z.; Gao, P.-X. A review of helical nanostructures: Growth theories, synthesis strategies and properties. Nanoscale 2014, 6, 9366–9400.
Wang, Y.; Xu, J.; Wang, Y.; Chen, H. Emerging chirality in nanoscience. Chem. Soc. Rev. 2013, 42, 2930–2962.
Nespolo, M.; Benahsene, A.H. Symmetry and chirality in crystals. J. Appl. Cryst. 2021, 54, 1594–1599.
Londoño-Calderon, A.; Williams, D.J.; Schneider, M.M.; Savitzky, B.H.; Ophus, C.; Ma, S.; Zhu, H.; Pettes, M.T. Intrinsic helical twist and chirality in ultrathin tellurium nanowires. Nanoscale 2021, 13, 9606–9614.
Porsev, V.V.; Bandura, A.V.; Lukyanov, S.I.; Evarestov, R.A. Expanded hexagonal nanohelicenes of zigzag morphology under elastic strain: A quantum chemical study. Carbon 2019, 152, 755–765.
Gingras, M. One hundred years of helicene chemistry. Part 1: Non-stereoselective syntheses of carbohelicenes. Chem. Soc. Rev. 2013, 42, 968–1006.
Tay, R.Y.; Park, H.J.; Lin, J.; Ng, Z.K.; Jing, L.; Li, H.; Zhu, M.; Tsang, S.H.; Lee, Z.; Teo, E.H.T. Concentric and Spiral Few-Layer Graphene: Growth Driven by Interfacial Nucleation vs Screw Dislocation. Chem. Mater. 2018, 30, 6858–6866.
Sun, H.; Kong, X.; Park, H.; Liu, F.; Lee, Z.; Ding, F. Spiral Growth of Adlayer Graphene. Adv. Mater. 2022, 34, 2107587.
Avdoshenko, S.M.; Koskinen, P.; Sevinçli, H.; Popov, A.A.; Rocha, C.G. Topological Signatures in the Electronic Structure of Graphene Spirals. Sci. Rep. 2013, 3, 1632.
Zhan, H.; Zhang, Y.; Yang, C.; Zhang, G.; Gu, Y. Graphene helicoid as novel nanospring. Carbon 2017, 120, 258–264.
Liu, R.; Zhao, J.; Wang, L.; Wei, N. Nonlinear vibrations of helical graphene resonators in the dynamic nano-indentation testing. Nanotechnology 2020, 31, 025709.
Zhu, C.; Ji, J.; Zhang, Z.; Dong, S.; Wei, N.; Zhao, J. Huge stretchability and reversibility of helical graphenes using molecular dynamics simulations and simplified theoretical models. Mech. Mater. 2021, 153, 103683.
Atanasov, V.; Saxena, A. Helicoidal graphene nanoribbons: Chiraltronics. Phys. Rev. B 2015, 92, 035440.
Newman, M.S.; Lednicer, D. The Synthesis and Resolution of Hexahelicene. J. Am. Chem. Soc. 1956, 78, 4765–4770.
Flammand-Barbieux, M.; Nasielski, J.; Martin, R.H. Synthesis of heptahelicene (1) benzophenanthrophenanthrene. Tetrahedron Lett. 1967, 7, 743–744.
Mori, K.; Murase, T.; Fujita, M. One-Step Synthesis of Helicene. Angew. Chem. Int. Ed. 2015, 127, 6951–6955.
Oña-Ruales, J.O.; Ruiz-Morales, Y.; Alvarez-Ramírez, F. The Helicenes: Potential Carriers of Diffuse Interstellar Bands. ACS Earth Space Chem. 2021, 5, 381–390.
Sabirov, D.S.; Tukhbatullina, A.A.; Shepelevich, I.S. Polarizability in Astrochemical Studies of Complex Carbon-Based Compounds. ACS Earth Space Chem. 2022, 6, 1–17.
Sabirov, D.S.; Ori, O.; Tukhbatullina, A.A.; Shepelevich, I.S. Structural Descriptors of Benzenoid Hydrocarbons: A Mismatch between the Estimates and Parity Effects in Helicenes. C 2022, 8, 42.
Lukmanov, T.; Akhmetov, A.G.; Sabirov, D.S. Polarizability of Kekulene, Septulene, and Nearest Non-Planar Polycyclic Aromatic Hydrocarbons. C 2022, 8, 61.
Pischel, I.; Grimme, S.; Kotila, S.; Nieger, M.; Vögtle, F. A configurationally stable pyrrolohelicene: Experimental and theoretical structure-chiroptic relationships. Tetrahedron Asymmetry 1996, 7, 109–116.
Buss, V.; Kolster, K. Electronic structure calculations on helicenes. Concerning the chirality of helically twisted aromatic systems. Chem. Phys. 1996, 203, 309–316.
Grimme, S.; Peyerimhoff, S.D. Theoretical study of the structures and racemization barriers of helicenes (n = 3–6, 8). Chem. Phys. 1996, 204, 411–417.
Schulman, J.M.; Disch, R.L. Aromatic Character of Helicenes and Phenacenes. J. Phys. Chem. A 1999, 103, 6669–6672.
Rulíšek, L.; Exner, O.; Cwiklik, L.; Jungwirth, P.; Starý, I.; Pospíšil, L.; Havlas, Z. On the Convergence of the Physicochemical Properties of Helicenes. J. Phys. Chem. C 2007, 111, 14948–14955.
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2004, 25, 1463–1473.
Klamt, A.; Schuurmann, G.J. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. Chem. Soc. Perkin Trans. 2 1993, 799–805.
Nishide, T.; Hayashi, S. Intrinsic Dynamic and Static Nature of π…π Interactions in Fused Benzene-Type Helicenes and Dimers, Elucidated with QTAIM Dual Functional Analysis. Nanomaterials 2022, 12, 321.
Jalaie, M.; Weatherhead, S.; Lipkowitz, K.B.; Robertson, D. Modulating force constants in molecular springs. Electron. J. Theor. Chem. 1997, 2, 268–272.
Šesták, P.; Wu, J.; He, J.; Pokluda, J.; Zhang, J. Extraordinary deformation capacity of smallest carbohelicene springs. Phys. Chem. Chem. Phys. 2015, 17, 18684–18690.
Tian, Y.-H.; Park, G.; Kertesz, M. Electronic Structure of Helicenes, C2S Helicenes, and Thiaheterohelicenes. Chem. Mater. 2008, 20, 3266–3277.
Treboux, G.; Lapstun, P.; Wu, Z.; Silverbrook, K. Electronic conductance of helicenes. Chem. Phys. Lett. 1999, 301, 493–497.
Wang, L.; Warburton, P.L.; Szekeres, Z.; Surjan, P.; Mezey, P.G. Stability and Properties of Polyhelicenes and Annelated Fused-Ring Carbon Helices: Models Toward Helical Graphites. J. Chem. Inf. Model. 2005, 45, 850–855.
Botek, E.; Champagne, B.; Turki, M.; André, J.-M. Theoretical study of the second-order nonlinear optical properties of helicenes and phenylenes. J. Chem. Phys. 2004, 120, 2042–2048.
He, Y.-Y.; Chen, J.; Zheng, X.-L.; Xu, X.; Li, W.-Q.; Yang, L.; Tian, W.Q. Spiral Graphene Nanoribbons with Azulene Defects as Potential Nonlinear Optical Materials. ACS Appl. Nano Mater. 2019, 2, 1648–1654.
Champagne, B. Helicenes and Nonlinear Optical Properties: A Good Match？. In Helicenes: Synthesis, Properties, and Applications; Crassous, J., Stará, I.G., Starý, I., Eds.; Wiley-VCH GmbH: Weinheim, Germany, 2022.
Vacek, J.; Chocholoušová, J.V.; Stará, I.G.; Starý, I.; Dubi, Y. Mechanical tuning of conductance and thermopower in helicene molecular junctions. Nanoscale 2015, 7, 8793–8802.
Guo, Y.-D.; Yan, X.-H.; Xiao, Y.; Liu, C.-S. U-shaped relationship between current and pitch in helicene molecules. Sci. Rep. 2015, 5, 16731.
Xu, X.; Li, W.; Zhou, X.; Wang, Q.; Feng, J.; Tian, W.Q.; Jiang, Y. Theoretical study of electron tunneling through the spiral molecule junctions along spiral paths. Phys. Chem. Chem. Phys. 2016, 18, 3765–3771.
Šmarhák, J.; Voves, J. Electronic transport properties of compressed and stretched helicene-graphene nanostructures, a theoretical study. Physica E 2022, 141, 115111.
Nakakuki, Y.; Hirose, T.; Matsuda, K. Theoretical Investigation on Electron Transport Capabilities of Helically Twisted Molecules Based on Decay Constants of Exchange Interaction. Chem. Lett. 2022, 51, 256–259.
Kiran, V.; Mathew, S.P.; Cohen, S.R.; Delgado, I.H.; Lacour, J.; Naaman, R. Helicenes—A New Class of Organic Spin Filter. Adv. Mater. 2016, 28, 1957–1962.
Dalum, S.; Hedegård, P. Theory of Chiral Induced Spin Selectivity. Nano Lett. 2019, 19, 5253–5259.
Pan, T.-R.; Guo, A.-M.; Sun, Q.-F. Spin-polarized electron transport through helicene molecular junctions. Phys. Rev. B 2016, 94, 235448.
Kettner, M.; Maslyuk, V.V.; Nürenberg, D.; Seibel, J.; Gutierrez, R.; Cuniberti, G.; Ernst, K.-H.; Zacharias, H. Chirality-Dependent Electron Spin Filtering by Molecular Monolayers of Helicenes. J. Phys. Chem. Lett. 2018, 9, 2025–2030.
Matxain, J.M.; Ugalde, J.M.; Mujica, V.; Allec, S.I.; Wong, B.M.; Casanova, D. Chirality Induced Spin Selectivity of Photoexcited Electrons in Carbon-Sulfur Helicenes. ChemPhotoChem 2019, 3, 770–777.
Xu, X.; Tian, R.; Wang, Q.; Li, W.; Jiang, Y.; Zhou, X.; Zhang, G.; Liu, L.; Tian, W.Q. Spatial manipulating spin-polarization and tunneling patterns in graphene spirals via periphery structural modification. Carbon 2017, 113, 325–333.
Lieb, E.H. Two theorems on the Hubbard model. Phys. Rev. Lett. 1989, 62, 1201–1204.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Chemistry, Physical

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Vitaly V. Porsev

Robert A. Evarestov

View Times: 371

Update Date: 14 Sep 2023

Table of Contents

Video Upload Options

Confirm

1. Introduction

2. Theoretical Consideration of Molecular Helicenes and Their Properties

References