Application of Artificial Intelligence Techniques in Rainfall Forecasting

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Muhammad Waqas	--	4581	2023-08-28 10:03:06	\|
2	references update	Fanny Huang	Meta information modification	4581	2023-08-29 03:56:45	\| \|
3	add full name of abbreviations	Fanny Huang	+ 18 word(s)	4599	2023-09-01 07:50:42	\|

This entry is adapted from the peer-reviewed paper 10.3390/w15162979

artificial intelligence machine learning deep learning neural networks rainfall forecasting

1. Introduction

Various rtificial intelligence techniques (AITs), including artificial neural networks (ANNs), support vector machine (SVM), and Fuzzy logic (FL), have been employed for rainfall forecasting. These techniques have been used to model the relationships between meteorological variables and rainfall and to predict future rainfall based on historical data. Many recent studies have employed AITs for rainfall forecasting and have achieved promising results ^[1]^[2]. Due to their ability to recognize complex patterns, record non-linear correlations, and handle vast amounts of meteorological data, AITs are extremely useful in rainfall forecasting. AITs increase the accuracy and adaptability of forecasts by iteratively improving predictive models, taking into account complex and dynamic meteorological events. Informed decision-making, effective resource allocation, proactive disaster preparedness, and ideal risk mitigation across several sectors are all made possible by this skill, which depends on precise rainfall estimates ^[2]. AITs have improved the accuracy of rainfall forecasts ^[3]. Recent studies have shown that AI techniques can capture complex non-linear relationships between meteorological variables and rainfall and perform better than traditional statistical models and machine learning (ML) techniques ^[4]^[5]. AI is a vast and inclusive domain in which ML is a distinct subfield. ANNs are a more specialized branch of ML, while deep learning (DL) emerges as a sophisticated and intricate component as one delves deeper into this framework. The relationship between AITs, ML, ANN, and DL is shown in Figure 1.

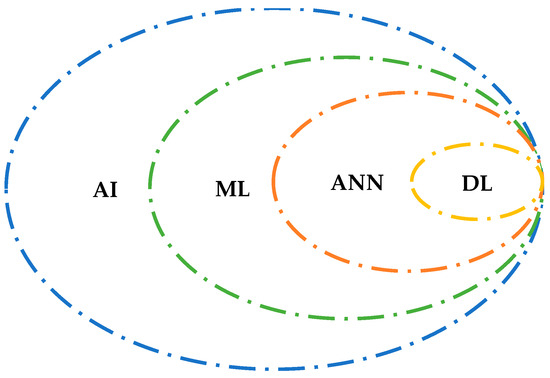
Figure 1. Relationship between artificial intelligence (AI), machine learning, artificial neural networks, and deep learning.

2. Machine Learning

ML is part of AI, which consists of algorithms that can be automatically trained and analyzed to build accurate models from specific datasets. The classification AI consisting of ML and DL is presented in Figure 2. Figure 2 depicts the hierarchical classification emerging within the ML field, embracing supervised, unsupervised, semi-supervised, and reinforcement learning methods. The commonly used supervised and unsupervised methodologies are particularly relevant to rainfall forecasting. After that, the supervised approach is subdivided into regression and classification, which are further subdivided into decision trees (DT), random forests (RFs), ANNs, DL, SVM, K-Nearest Neighbors (KNN), and Bayesian methods. Notably, a finer classification occurs within the domain of DL, separating feed-forward neural networks (FFNN), wavelet neural networks (WNNs), deep neural networks (DNNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs) as distinct subcategories. Unsupervised ML, on the other hand, is divided into two categories: clustering methods, which include k-means, hierarchical, and fuzzy c-means, and dimensionality reduction techniques, which include singular value decomposition (SVD, principal component analysis (PCA) and independent component analysis (ICA). This sophisticated hierarchy of classifications provides a thorough framework for understanding the numerous disciplines and subfields within AI and ML, laying the groundwork for later study and analysis in the context of rainfall forecasting.

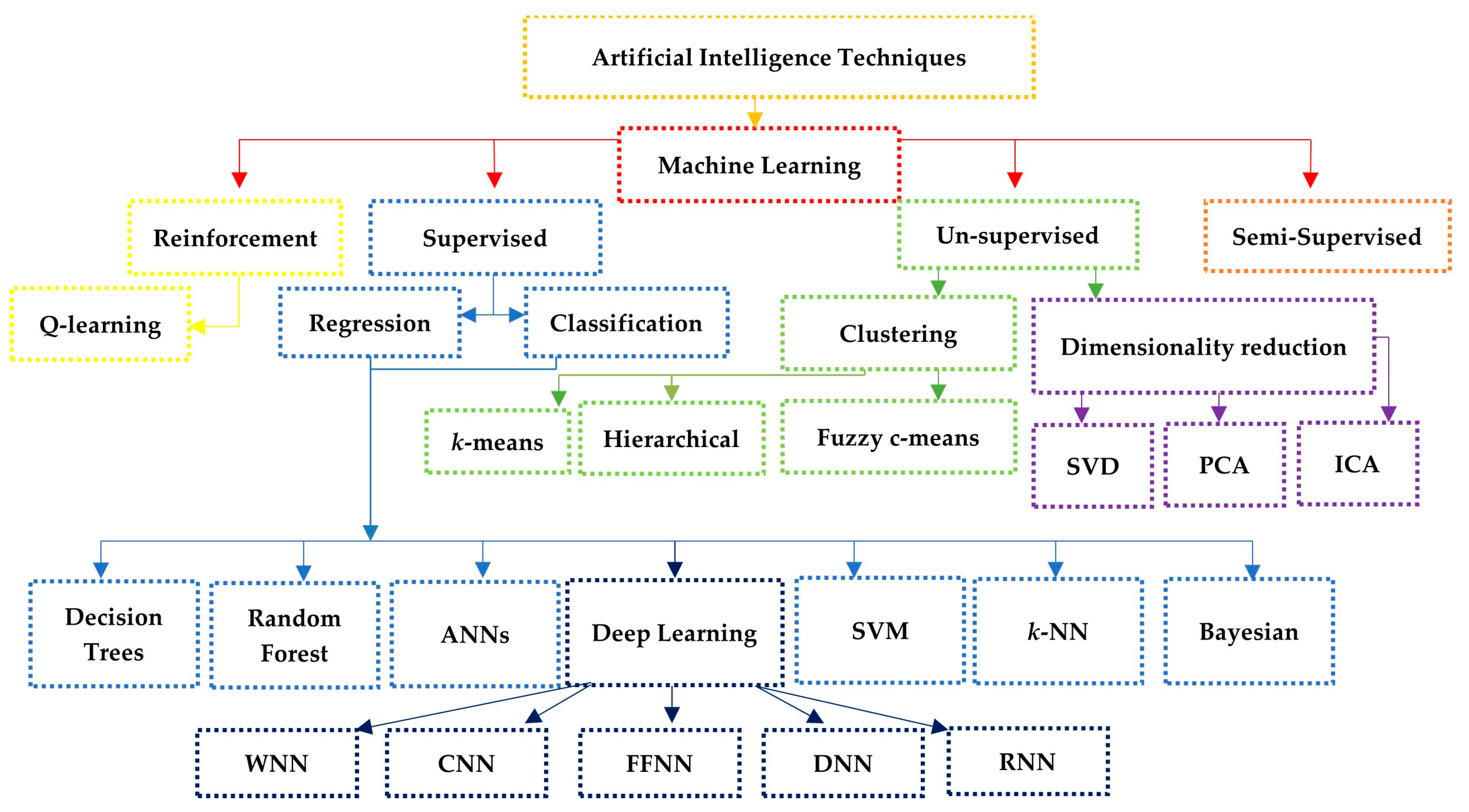
Figure 2. Classification AITs, including ML and DL.

Various rainfall forecasting applications have utilized supervised learning, including short- and long-term weather prediction, flood forecasting, and drought surveillance. Unsupervised learning is a technique for ML wherein the algorithm learns from the nature of datasets. Without prior knowledge of the outcome, the algorithm discovers connections and patterns within the data ^[6]. Due to their ability to discover relationships and patterns from data, ML algorithms are a popular option for rainfall forecasting. ML models have been applied to forecasting short- and long-term rainfall ^[7].

2.1. Support Vector Machines (SVMs)

SVMs rely on supervised learning algorithms for classification, time series, and regression analysis. Due to their capacity to deal with complex connections between factors and noisy data, SVMs have been extensively employed for rainfall forecasting. SVMs function by mapping datasets of higher-dimensional space and locating a hyperplane that divides data points into distinct classes ^[8]. A SVM was proposed by ^[9] to overcome the obstacles related to prediction. ANNs aim to lower training errors, whereas SVMs aim to reduce generalization errors. These techniques accomplish the utmost achievable level of accuracy in their disciplines. Compared to ANNs, SVMs are based on structure-based risk minimization instead of empirical risk minimization. The SVM approach follows a logical progression: (1) inclusion of the input dataset; (2) iterative examination of various model compositions involving predictor and target variables; (3) execution of training and testing stages; (4) selection of an appropriate kernel function; (5) accommodation of multi-class scenarios through diverse constraint combinations; and (6) use of v-fold cross-validation to ensure robust testing and validation. Finally, the process results in: (7) identification of the most capable SVM model through extensive v-fold cross-validation, producing informative results for display and analysis ^[5].

Support Vector Regression (SVR) is a subset of SVMs used for regression analysis. Numerous studies have used SVR for rainfall forecasting, including Vafakhah et al. (2020). The authors used SVR to forecast daily rainfall in Iran. The study discovered that SVR outperformed the conventional methods, including multiple linear regression and ANNs ^[10].

Multi-Kernel SVR is a variation of SVR that uses multiple kernel functions to detect various data patterns ^[11]. Numerous studies have used it for rainfall forecasting, including Caraka et al. (2019), who used multi-Kernel SVR seasonal autoregressive integrated moving average (MKSVR-SARIMA) to forecast daily rainfall in Manado, North Sulawesi provinces in Indonesia. The study revealed that MKSVR-SARIMA excelled over other conventional techniques ^[12].

A SVM with a Firefly Algorithm (SVM-FA) is a type of SVM that employs the FA, a meta-heuristic optimization algorithm, for fine-tuning the SVM model’s parameters ^[13]. Numerous studies have used the SVM-FA for rainfall forecasting, including Danandeh Mehr et al. (2019), who used the SVM-FA hybrid model for monthly rainfall in northwest Iran. The findings determined that SVM-FA outperformed its competitors with a 30% reduction in root means square error (RMSE) and a 100% boost in Nash-Sutcliffe efficiency (NSE). The authors recommend this model for monthly rainfall in semiarid regions ^[14].

SVMs have proven useful in rainfall forecasting but have several limitations. These limitations include their sensitivity to parameter selection, limited interpretability, limited handling of missing data, limited handling of non-linear relationships, limited scalability, and limited handling of multiple outputs ^[15]. To overcome these limitations, researchers may need to develop new techniques to improve the interpretability of SVMs, handle missing data and non-linear relationships more effectively, and develop new approaches to handle large datasets and multiple outputs. Overall, SVMs remain a valuable tool for rainfall forecasting, but they should be employed in conjunction with other machine learning algorithms to capture the full range of relationships between variables ^[15].

2.2. Decision Trees (DTs)

DTs have been used for rainfall, flood forecasting, and drought monitoring ^[4]^[16]. The process of DTs described by Humphries et al. (2022): data separating and error eradication proceed until the terminal node is reached or the dataset misclassification error at the termination of the terminal node becomes zero. At this point, further data splitting will discontinue. The output value is displayed on the terminal node generation’s display ^[16].

For instance, Dou et al. (2019) analyzed and contrasted the efficacy of two cutting-edge machine learning models, DT and random forest (RF) technology, to model the massive rainfall-triggered landslide events in the Izu-Oshima Volcanic Island, Japan, on a regional scale. The RF and DT models can be utilized in similar non-eruption-related landslide investigations in tephra-rich volcanoes because they can rapidly generate precise and stable LSM maps for threat management and decision-making ^[17].

In Pakistan’s Mangla watershed, Humphries et al. (2022) used decision tree forests, tree boosts, and solitary decision trees to estimate the rainfall runoff. The authors used meteorological records like the temperature, humidity, and runoff datasets to forecast rainfall runoff. The results indicated that the decision tree could forecast the rainfall-runoff process more precisely than the other methods ^[16].

In another study, Ahmadi et al. (2022) propose a new sequential minimal optimization (SMO) that develops ensembles for rainfall prediction utilizing random committee (RC), Dagging (DA), and additive regression (AR) models. In Kermanshah, Iran, a synoptic station was in operation between 1988 and 2018, and they collected thirty years’ monthly datasets, including the highest and lowest relative humidity rates, temperatures, evaporation data, sunlight hours, wind speed, and rainfall. This study demonstrated that the DA-SMO ensemble algorithm outperformed the others ^[18].

Gulati et al. (2016) mentioned that DTs have limitations, including overfitting, instability, and bias. Researchers may need to develop new techniques to defeat the limits and enhance the accuracy and robustness of DTs in prediction applications ^[19].

2.3. Random Forest (RF)

RF is a powerful ML algorithm widely used in various fields, including rainfall prediction ^[20]. RF is a technique for ensemble learning which utilizes multiple decision trees to make precise predictions ^[21]. RF has been utilized in several aspects of rainfall forecasting, including rainfall estimations, drought prediction, and flash flood forecasting. Using Malaysian data, Zainudin et al. (2016) investigated a variety of classifiers to forecast rainfall, including Nave Bayes, SVM, DT, ANNs, and RF. The results showed that RF outperformed the other ML algorithms ^[20].

In another investigation, Pham et al. (2019) compared linear discriminant analysis (LDA), RF, and support vector classification for rainfall-state classification. The results indicate that RF is superior to LDA and SVC for classifying rainfall states. Using RF for three-state rainfall classification and LS-SVR for rainfall-amount forecasting can enhance the downscaling of extreme rainfall ^[22].

The objective of the proposed research by Primajaya and Sari (2018) was to establish a model utilizing the RF algorithm. The application of RF on the training set resulted in a model with an accuracy of 71.09%. An f-measure of 0.79, recall of 0.85, and precision of 0.75 further demonstrate the model’s performance. The kappa statistic is 0.33, with a mean absolute error (MAE) of 0.35 and a root mean squared error (RMSE) of 0.46 for the model. Furthermore, the receiver operating characteristic curve (ROC) area is 0.78, demonstrating the resilience of the RF method. Implementing the RF algorithm with 10-fold cross-validation produced output with an accuracy of 99.45%, precision of 0.99, recall of 0.99, f-measurement of 0.99, kappa statistic of 0.99, MAE of 0.09, RMSE of 0.14, and ROC area of 1 ^[23].

RF is a powerful ML algorithm that is extensively employed in rainfall forecasting. Nonetheless, RF has limitations, such as a lack of interpretability, limited support for multiple outputs, and restricted scalability. Researchers may need to develop new techniques to enhance the interpretability of radio frequency (RF) data and more effectively manage multiple outputs and large datasets ^[24].

2.4. Artificial Neural Networks (ANNs)

ANNs are commonly implemented in rainfall forecasting. ANNs have been implemented in numerous applications. The ANN model attempts to link the data inputs and the outputs projected for the forthcoming period without employing predefined coding. It is suitable for weather forecasting because of the random and unpredictable nature of the weather’s characteristics and the intricate nature of the systems ^[25]. This network has three layers, as shown in Figure 3: output, input, and hidden layers.

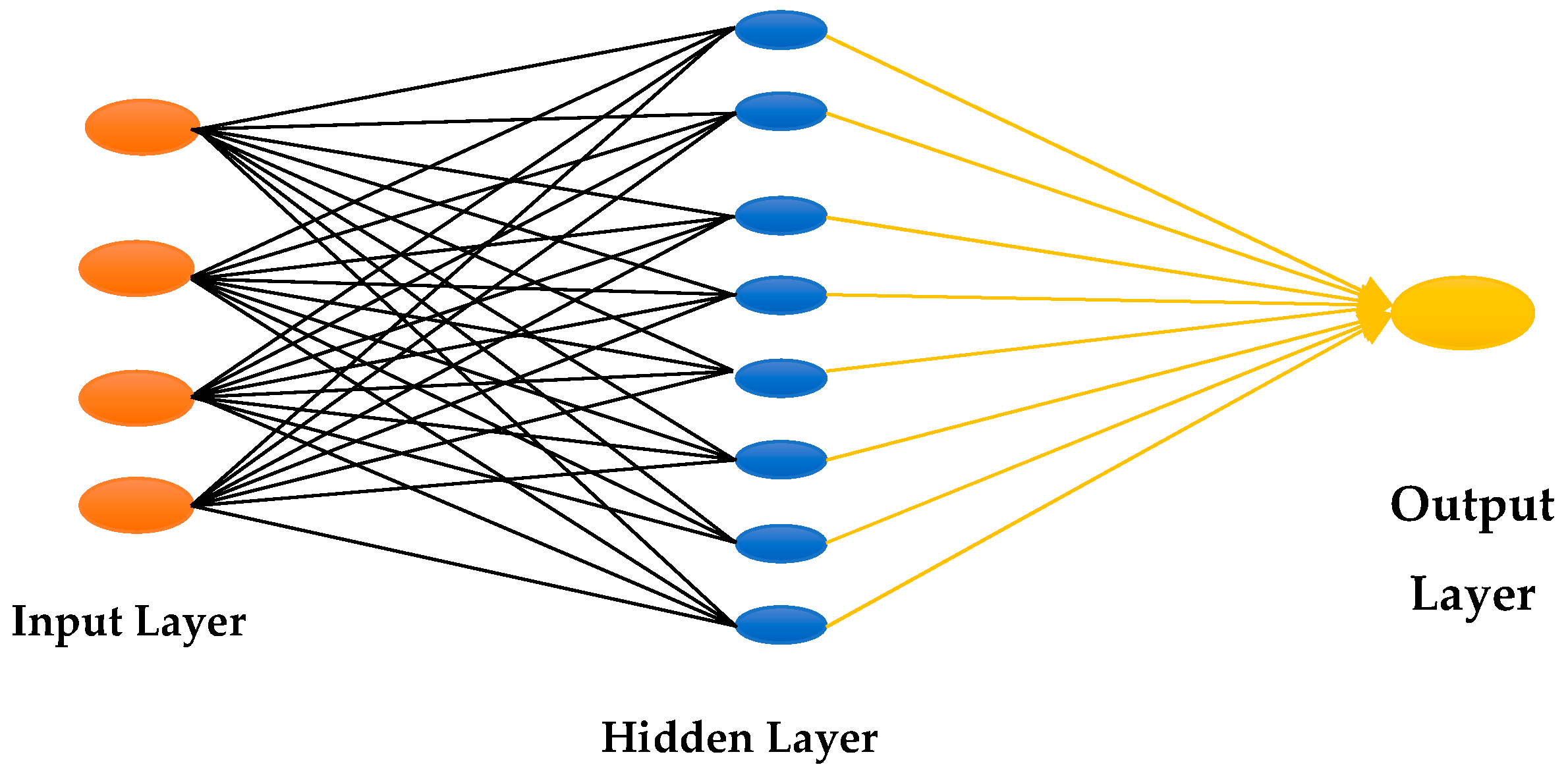
Figure 3. Schematic representation of ANN.

Hsieh et al. (2019) employed a hybrid model of ANN and multiple regression analysis (MRA) to predict the total typhoon rainfall and groundwater-level rise in the Zhuoshui River basin. Using data from gauge stations in eastern Taiwan and open-source typhoon data, the authors constructed an ANN model to predict the total rainfall and groundwater level during a typhoon encounter; they then revised the predictive values using MRA. The results demonstrated that the ANNs accurately and dependably predicted rainfall ^[26].

Hossain et al. (2020) assessed the effectiveness of MLR and ANN in modeling long-term seasonal rainfall patterns in Western Australia. The oceanic climate variables El Niño Southern Oscillation and Indian Ocean Dipole were viewed as potential seasonal rainfall forecasters based on their time series data. The methodologies were utilized at three Western Australia rainfall stations. As expected, the ANN models outperformed the MLR models regarding the Pearson correlation and statistical error when estimating Western Australia’s spring rainfall ^[27].

ANNs have limitations, including overfitting, computational complexity, and interpretability. Researchers may need to develop new techniques to improve the interpretability of ANNs and handle large datasets more effectively. Overall, ANNs remain a valuable tool for rainfall forecasting, and their applications will likely expand ^[28].

2.5. K-Nearest Neighbors

A supervised ML algorithm k-NN can handle classification and regression problems. The k-NN algorithm assigns data points to the same class when they are close together, or there is an obvious distinction between classes. k-NN uses the Euclidean distance formula to determine the distance between two graph nodes. An advantage of k-NN for rainfall data is that record points can be quickly trained and categorized with minimal tuning ^[29].

k-NN has been used for various aspects of rainfall forecasting. Wu et al. (2010) utilized k-NN to predict extreme rainfall events in China’s Pearl River Basin. The authors predicted extreme rainfall events using meteorological variables. The results indicated that k-NN could predict extreme rainfall events with excellent precision and efficacy ^[30].

Using pattern similarity-based models and the k-NN technique, Sharma and Bose (2014) forecasted the monthly rainfall based on historical data to compare the predicted values with the observed data. They utilized a recently proposed method for rainfall forecasting, Approximation, as well as Prediction of Stock Time-series Data (APST). In addition, they presented two variants of the APST. These techniques are superior to the original APST and AR models ^[31].

k-NN has limitations, including the choice of K, computational intensity, and sensitivity to outliers. Researchers may need to develop new techniques to overcome these limitations and enhance the accuracy and robustness of k-NN in rainfall forecasting applications ^[32].

2.6. Bayesian Methods

Bayesian methods have been increasingly applied in rainfall forecasting due to their ability to integrate prior knowledge and uncertainty in the modeling process ^[33]. Various aspects of rainfall forecasting have utilized Bayesian methods. For example, Nikam and Meshram (2013) used an anticipated and implemented data-intensive model in conjunction with data mining to predict rainfall resources. They utilized a Bayesian method and discovered it to be effective and accurate. The study demonstrated that Bayesian models could predict rainfall with high precision and accuracy ^[33].

Khan and Coulibaly (2006) proposed a Bayesian method for training a multilayer feed-forward neural network (FFNN) for generating reservoir inflow and daily river flow in a Canadian river basin. The Bayesian neural network (BNN) model worked better than the theoretical model and performed marginally better than the conventional ANN model when simulating peak, mean, and basin inflows and low river flows. It is demonstrated that BNN models provide accurate reservoir inflow and streamflow forecasts without sacrificing model forecast precision when matched to a conventional ANN and the proposed framework Hydrologiska Byråns Vattenbalansavdelning (HBV) model. The Bayesian learning algorithm automatically manages overfitting and underfitting, which are serious problems with traditional ANN learning algorithms. This is a significant advantage of the BNN approach ^[34].

Kaewprasert et al. (2022) computed credible and highest posterior density (HPD) estimates for the average and alteration among the means of delta-gamma distributions and a confidence interval based on fiducial values using Bayesian technique based on Jeffrey’s rule and uniform priors. Based on the simulation outcomes, the Bayesian HPD predicted the shortest duration and performed well regarding coverage probability. Rainfall statistics from the Chiang Mai region of Thailand demonstrate the suggested technologies’ effectiveness ^[35].

Bayesian methods also have limitations, including computational complexity, the choice of the prior distribution, and model complexity. Researchers may need to develop new techniques to overcome these limitations and enhance the accuracy and robustness of Bayesian methods in rainfall forecasting applications ^[36].

3. Deep Learning

DL is a subcategory of supervised ML. DL employs multi-layered data learning methodologies. These layers are arranged using non-linear modules to obtain the optimal solution with the least loss ^[37]. The information processing and communicating processes are based on human nerves ^[38]. DL’s primary job is to analyze and extract characteristics from datasets to generate accurate models. DL applications include image analysis and processing, natural language processing, handwriting identification, social media sentiment analysis, and prediction and forecasting. The universal architecture of deep neural networks is illustrated in Figure 4.

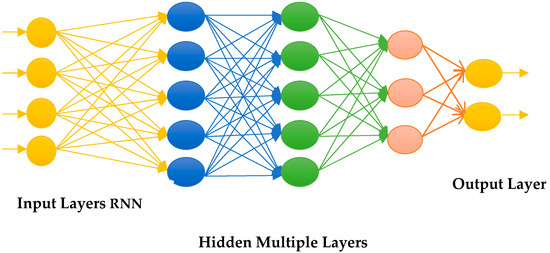
Figure 4. Architecture of Deep neural networks.

3.1. Convolutional Neural Networks (CNNs)

The CNN is a deep neural network commonly used for image recognition, but it is also employed for time-series forecasting problems. The CNN is designed to automatically learn characteristics from input data by applying convolution and pooling operations. Convolution is the process of extracting local attributes of the input data and pooling them to reduce the dimensionality of the data. By stacking multiple convolutional and pooling layers, the CNN can learn hierarchical features from the input data and generate predictions ^[39].

Narejo et al. (2021) employed a modified form of the CNN to the time series estimation task for the eight-day ahead prediction rainfall series. Three filters with a kernel size of (3, 1) were used. The first and second convolution layers contain ten filters of the same dimensions (3, 1). Following the “average” methodology for subsampling, the pooling layer was added. In this instance, however, the average factor was one. The tangent hyperbolic activation function was used for entirely connected layers, followed by a linear layer for output predictions. The authors utilized MSE to determine the most accurate forecasting model. The authors’ proposed model yielded encouraging results ^[40].

Recent studies employing the CNN for rainfall forecasting have yielded promising results. Elhoseiny et al. (2015) investigated how the CNN could identify weather from images and assessed the identification output of the ImageNet-CNN and weather-trained CNN layers. The model outperformed the most recent weather classification technology by a wide margin. They also examined the behavior of all CNN layers and uncovered some intriguing results ^[41].

Using climate data, Liu et al. (2016) showed that deep learning could predict extreme weather patterns. A CNN architecture with a high depth level was devised to identify tropical cyclones and atmospheric rivers. This optimistic implementation may resolve multiple pattern detection issues in climate science. The DNN produces high-level algorithms directly from the data, thus preventing the use of subjective conventional adaptive threshold criteria for detecting climate-dependent events. The outcomes of this investigation are used to assess the current and potential developments in climate extreme weather events and investigate changes in the thermodynamics and dynamics of such events as an outcome of global warming ^[42].

The CNN has some drawbacks, such as its need for a large quantity of data and its black-box nature. Nonetheless, with the increase in the availability of weather information and the creation of novel interpretability techniques, the CNN has great potential in rainfall forecasting ^[43].

3.2. Feed-Forward Neural Networks (FFNNs)

The FFNN is a form of ANN commonly applied to time-series forecasting issues. An input layer, one or more concealed layers, and an output layer comprise the FFNN. Each layer comprises one or more interconnected neurons with neurons in the layer beneath it. Setting the connection weights among neurons within each layer, the FFNN learns to forecast the output ^[44].

Recent research has used FFNNs for rainfall forecasting with promising results. Paras et al. (2009) forecasted relative humidity and maximum and minimum temperatures using time series analysis. A back-propagation multilayer FFNN was used. They found FFNNs to be superior to other methods, with better results ^[45].

Velasco et al. (2019) developed a week-ahead rainfall forecast employing a multilayer perceptron neural network (MLPNN) to assess historic rainfall records. After model installation, data preparation, and performance assessment, two MLPNN models predicted the rainfall in the following weeks. The MLPNN supervised the FFNN with 11 input neurons indicating meteorological data, concealed neurons, and seven output neurons indicating the week’s forecast. Sigmoid transfer function (SCG) and SCG-Tangent MLPNN models had MAE and RMSE of 0.0127 and 0.1388, or 0.01512 and 0.01557, respectively ^[46].

Recent studies demonstrated that the FFNN could capture complex data relationships and accomplish them better than traditional statistical models ^[45]^[46]^[47]. The FFNN does, however, have significant drawbacks, including overfitting and being a black-box model. However, with the expansion of rainfall data and the creation of new interpretability tools, such as the use of feed-forward in predicting rainfall, ANNs have much potential ^[48].

3.3. Recurrent Neural Networks (RNNs)

A subset of ANNs called an RNN is designed to handle sequential data, such as time-series data. In contrast to feed-forward neural networks, which analyze each input independently, RNNs contain a memory component that enables them to keep account of earlier inputs in the sequence. Therefore, they are ideally adapted for activities like rainfall forecasting, where the current prediction relies on earlier measurements ^[49].

RNNs, unlike traditional ANNs, have connected neurons in recurrent layers. Thus, information from a neuron is conveyed to neurons in similar layers above or below. RNNs also contain a concealed state for recalling sequence data. RNNs approximate new states by recursively applying activation functions to previous states and new inputs.

The RNN is an efficient model for time series forecasting because its feedback connections can transmit information from one input to the next, simulating the dynamic behavior of the data sequence. However, a straightforward or shallow RNN frequently faces the issue of gradients that vanish. It cannot simulate long-term trends and impairs the network as a result. The gradient-diminishing issues in RNNs have been addressed in recent years by the more expensive long short-term memory (LSTM) neural network ^[50].

Many recent research investigations have used the RNN to predict rainfall with promising results. Dong et al. (2021) forecasted the daily average air temperature of the four (RNNs) using a model which incorporates convolutional neural networks (CNNs) and RNNs. Between 1952 and 2018, the convolutional recurrent neural network (CRNN) was trained using daily air temperature measurements over China. Using historical air temperature data, their model could precisely predict the air temperature ^[51].

Similarly, Poornima and Pushpalatha (2019) introduced an Intensified LSTM-based RNN for predicting rainfall. The neural network is proficient and was evaluated by applying a standard rainfall record. The network was trained to forecast the characteristics of rainfall. The precision, epochs number, loss, and network learning rate are considered when assessing the performance and efficacy of the planned rainfall prediction model. The results are compared to the Holt–Winters, Extreme Machine Learning, autoregressive integrated moving average (ARIMA), LSTM, and RNN models to illustrate the improvement in rainfall forecast ^[52].

Utilizing RNNs to improve the accuracy of rainfall forecasts is a prospective research topic. Recent research has demonstrated that RNNs outperform conventional statistical approaches and FFNNs, indicating that they capture better complex non-linear correlations in the data. However, RNNs have disadvantages, such as the prospect of gradients vanishing or exploding and the need for expensive computation ^[49].

3.4. Deep Neural Networks (DNNs)

Due to DNNs’ ability to process big datasets and learn complicated non-linear correlations, DNNs have become a useful tool for time-series forecasting tasks. DNNs are superior to shallow neural networks (SNNs) because of their ability to learn more complex data representations, making them useful for tasks like rainfall forecasting, where the connections between meteorological parameters and rainfall can be highly non-linear ^[53].

Recent DNN rainfall forecasting tests have yielded promising results. Weesakul et al. (2021) tested machine learning’s monthly rainfall forecasting using DNN. Due to its long-term rainfall data, the Ping River basin in northern Thailand was chosen for the study. The monthly rainfall between 1975 and 2018 was analyzed at six river basin rainfall sites. The efficacy of the model was evaluated using the stochastic efficiency (SE) and correlation coefficient (r). According to previous research, the 24 large-scale atmospheric variables (LAV) employed as predictors in the DNN model associated relationships with seasonal rainfall in the Ping River basin. The initial simulation utilizing all 24 LAV of the validation period (2009–2019) to estimate the six-month rainfall in stations one year in the future demonstrates that the DNN can make predictions with an accuracy range of 58% to 72% and a correlation coefficient of 0.59 to 0.80. The input selection enhanced the prediction by decreasing the input LAV range from 24 to 13. In the next simulation with input selection, the DNN provided more accurate one-year forecasts with stochastic efficiencies ranging between 69% and 78% and correlation coefficients ranging, in all stations, between 0.75 and 0.82 ^[7].

Barman et al. (2021) evaluated the use of linear regression, SVR, and DNN for rainfall forecasts in Guwahati. The study utilized the daily rainfall data from Guwahati, Assam, India. Daily meteorological data were used in this study. The RMES, MAE, and MSE were compared with the DNN, LR, and SVR. The MSE and RMSE are lower for the DNN model than for the LR and SVR, but the SVR outperforms MAE. Regardless of the proportion of trainings to test rainfall statistics, both models are superior ^[54]. DNNs could improve rainfall forecasts. Recent research has demonstrated that DNNs can learn complicated non-linear correlations in data and outperform statistical models and other neural network architectures. DNNs can overfit and are computationally expensive ^[53].

3.5. Wavelet Neural Networks (WNNs)

WNNs are a wide range of ANNs that model time series data by combining wavelet analysis and neural networks ^[55]. WNNs use wavelet analysis and neural networks to model time series data. Time series data is decomposed using wavelet analysis to create several frequency bands, each of which can be utilized to detect unique patterns ^[56].

Recent studies have utilized WNNs extensively for rainfall forecasting, with promising results. Different models evaluated by Estévez et al. (2020), which combine wavelet analysis (multiscalar decomposition) and ANNs, have been tested on sixteen sites across southern Spain (Andalusia region, which is semiarid), each representing a climate and landscape that is distinct from the others. Ten WNNs were deployed to forecast the monthly rainfall, and were evaluated using short-term thermo-pluviometric time series. This is conceivable due to the competence of wavelets to characterize non-linear signals. Although each of the evaluated sites had satisfactory results, there are discrepancies between the forecasts of the ten models ^[56].

Wang et al. (2017) developed a WNN-based model for daily rainfall forecasting using meteorological data. They used the Discrete Wavelet Transform (DWT) to split the weather data into different frequency bands and then taught a neural network the relations between the decomposed signals and the rainfall. They performed more effectively than conventional statistical models and other neural network architectures ^[57].

Similarly, Venkata Ramana et al. (2013) attempted to discover an alternate solution for rainfall forecasting by merging the wavelet technique and ANN. The WNN models were applied to the Darjeeling rain gauge station’s monthly rainfall data. Statistical methods were employed to assess the validation and calibration performance of the models. The results of modeling the monthly rainfall series indicate that WNNs are more effective than ANN models ^[58].

Partal et al. (2015) investigated three different NN algorithms (feed-forward back-propagation, FFBP; radial basis function; generalized regression neural network) and wavelet transformation for predicting daily rainfall. Various input combinations for rainfall estimation were evaluated. Consequently, the optimal neural network model was determined for each station. In addition, the effectiveness of linear regression models and wavelet neural network models are compared. It was discovered that the wavelet FFBP procedure provides the superlative performance assessment criteria. The findings designate that the coupling wavelet alters with neural networks that deliver significant estimation process advantages. In addition, the worldwide wavelet spectrum delivers essential evidence regarding the physical process being modeled ^[59].

WNNs also have some drawbacks, including computational expense and the possibility of overfitting. However, with novel training techniques and hardware, WNNs have tremendous potential in rainfall forecasting ^[56]^[60].

SVMs excel at managing complex data and preventing overfitting, but they can be difficult to interpret and struggle with missing data. DTs are effective for real-time forecasting, although they are susceptible to overfitting and biases. RF can handle non-linear correlations and missing data but lack interpretability, whereas ANNs can handle non-linear patterns but face issues such as overfitting and computational complexity. Deep Learning technologies, such as CNNs, improve the accuracy but require a large amount of data and lack transparency. WNNs show potential in managing big, non-linear data for rainfall prediction but still require safeguards against overfitting. RNNs can handle sequential data but face gradient problems, while RNNs can handle sequence data but encounter gradient problems. By processing vast amounts of meteorological data, identifying intricate patterns, and developing flexible ML and DL models, AITs significantly improve rainfall predictions. Ultimately, these AITs enable better resource allocation, risk mitigation, and disaster preparedness, resulting in cost savings, effective resource management, and increased societal resilience.

References

Bewoor, L.A.; Bewoor, A.; Kumar, R. Artificial intelligence for weather forecasting. In Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2021; pp. 231–239.
Al-Qammaz, A.; Darabkh, K.A.; Abualigah, L.; Khasawneh, A.M.; Zinonos, Z. An ai based irrigation and weather forecasting system utilizing lorawan and cloud computing technologies. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Russia, 26–29 January 2021; pp. 443–448.
Hernández, E.; Sanchez-Anguix, V.; Julian, V.; Palanca, J.; Duque, N. Rainfall prediction: A deep learning approach. In Proceedings of the Hybrid Artificial Intelligent Systems: 11th International Conference, HAIS 2016, Seville, Spain, 18–20 April 2016; pp. 151–162.
Waqas, M.; Shoaib, M.; Saifullah, M.; Naseem, A.; Hashim, S.; Ehsan, F.; Ali, I.; Khan, A. Assessment of advanced artificial intelligence techniques for streamflow forecasting in Jhelum River Basin. Pak. J. Agric. Res. 2021, 34, 580.
Waqas, M.; Bonnet, S.; Wannasing, U.H.; Hlaing, P.T.; Lin, H.A.; Hashim, S. Assessment of Advanced Artificial Intelligence Techniques for Flood Forecasting. In Proceedings of the 2023 International Multi-disciplinary Conference in Emerging Research Trends (IMCERT), Karachi, Pakistan, 4–5 January 2023; pp. 1–6.
Kunjumon, C.; Nair, S.S.; Suresh, P.; Preetha, S. Survey on weather forecasting using data mining. In Proceedings of the 2018 Conference on Emerging Devices and Smart Systems (ICEDSS), Tamilnadu, India, 2–3 March 2018; pp. 262–264.
Weesakul, U.; Chaiyasarn, K.; Mahat, S. Long-term rainfall forecasting using deep neural network coupling with input variables selection technique: A case study of Ping River Basin, Thailand. Eng. Appl. Sci. Res. 2021, 48, 209–220.
Yin, G.; Yoshikane, T.; Yamamoto, K.; Kubota, T.; Yoshimura, K. A support vector machine-based method for improving real-time hourly precipitation forecast in Japan. J. Hydrol. 2022, 612, 128125.
Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999.
Vafakhah, M.; Khosrobeigi Bozchaloei, S. Regional analysis of flow duration curves through support vector regression. Water Resour. Manag. 2020, 34, 283–294.
Gönen, M.; Alpaydın, E. Multiple kernel learning algorithms. J. Mach. Learn. Res. 2011, 12, 2211–2268.
Caraka, R.E.; Bakar, S.A.; Tahmid, M. Rainfall forecasting multi kernel support vector regression seasonal autoregressive integrated moving average (MKSVR-SARIMA). AIP Conf. Proc. 2019, 2111, 020014.
Chao, C.-F.; Horng, M.-H. The construction of support vector machine classifier using the firefly algorithm. Comput. Intell. Neurosci. 2015, 2015, 212719.
Danandeh Mehr, A.; Nourani, V.; Karimi Khosrowshahi, V.; Ghorbani, M.A. A hybrid support vector regression–firefly model for monthly rainfall forecasting. Int. J. Environ. Sci. Technol. 2019, 16, 335–346.
Karamizadeh, S.; Abdullah, S.M.; Halimi, M.; Shayan, J.; Javad Rajabi, M. Advantage and drawback of support vector machine functionality. In Proceedings of the 2014 International Conference on Computer, Communications, and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014; pp. 63–65.
Humphries, U.W.; Ali, R.; Waqas, M.; Shoaib, M.; Varnakovida, P.; Faheem, M.; Hlaing, P.T.; Lin, H.A.; Ahmad, S. Runoff Estimation Using Advanced Soft Computing Techniques: A Case Study of Mangla Watershed Pakistan. Water 2022, 14, 3286.
Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346.
Ahmadi, H.; Aminnejad, B.; Sabatsany, H. Application of machine learning ensemble models for rainfall prediction. Acta Geophys. 2022, 71, 1775–1786.
Gulati, P.; Sharma, A.; Gupta, M. Theoretical study of decision tree algorithms to identify pivotal factors for performance improvement: A review. Int. J. Comput. Appl. 2016, 141, 19–25.
Zainudin, S.; Jasim, D.S.; Bakar, A.A. Comparative analysis of data mining techniques for Malaysian rainfall prediction. Int. J. Adv. Sci. Eng. Inf. Technol. 2016, 6, 1148–1153.
Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32.
Pham, Q.B.; Yang, T.-C.; Kuo, C.-M.; Tseng, H.-W.; Yu, P.-S. Combing random forest and least square support vector regression for improving extreme rainfall downscaling. Water 2019, 11, 451.
Primajaya, A.; Sari, B.N. Random forest algorithm for prediction of precipitation. Indones. J. Artif. Intell. Data Min. 2018, 1, 27–31.
Statnikov, A.; Wang, L.; Aliferis, C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinform. 2008, 9, 1–10.
Cai, B.; Yu, Y. Flood forecasting in urban reservoir using hybrid recurrent neural network. Urban Clim. 2022, 42, 101086.
Hsieh, P.-C.; Tong, W.-A.; Wang, Y.-C. A hybrid approach of artificial neural network and multiple regression to forecast typhoon rainfall and groundwater-level change. Hydrol. Sci. J. 2019, 64, 1793–1802.
Hossain, I.; Rasel, H.; Imteaz, M.A.; Mekanik, F. Long-term seasonal rainfall forecasting using linear and non-linear modelling approaches: A case study for Western Australia. Meteorol. Atmos. Phys. 2020, 132, 131–141.
ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123.
Ghorpade, P.; Gadge, A.; Lende, A.; Chordiya, H.; Gosavi, G.; Mishra, A.; Hooli, B.; Ingle, Y.S.; Shaikh, N. Flood Forecasting Using Machine Learning: A Review. In Proceedings of the 2021 8th International Conference on Smart Computing and Communications (ICSCC), Kochi, India, 1–3 July 2021; pp. 32–36.
Wu, C.; Chau, K.W.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167.
Sharma, A.; Bose, M. Rainfall prediction using k-NN based similarity measure. In Proceedings of the Recent Advances in Information Technology: RAIT-2014 Proceedings, Dhanbad, India, 13–15 March 2014; pp. 125–132.
Papanikolaou, M.; Evangelidis, G.; Ougiaroglou, S. Dynamic k determination in k-NN classifier: A literature review. In Proceedings of the 2021 12th International Conference on Information, Intelligence, Systems & Applications (IISA), Chania Crete, Greece, 12–14 July 2021; pp. 1–8.
Nikam, V.B.; Meshram, B. Modeling rainfall prediction using data mining method: A Bayesian approach. In Proceedings of the 2013 Fifth International Conference on Computational Intelligence, Modelling and Simulation, Seoul, Republic of Korea, 24–25 September 2013; pp. 132–136.
Khan, M.S.; Coulibaly, P. Bayesian neural network for rainfall-runoff modeling. Water Resour. Res. 2006, 42.
Kaewprasert, T.; Niwitpong, S.-A.; Niwitpong, S. Bayesian estimation for the mean of delta-gamma distributions with application to rainfall data in Thailand. PeerJ 2022, 10, e13465.
Norton, J.D. Challenges to Bayesian confirmation theory. In Philosophy of Statistics; Elsevier: Amsterdam, The Netherlands, 2011; pp. 391–439.
Aftab, S.; Ahmad, M.; Hameed, N.; Bashir, M.S.; Ali, I.; Nawaz, Z. Rainfall prediction using data mining techniques: A systematic literature review. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 143–150.
Aftab, S.; Ahmad, M.; Hameed, N.; Bashir, M.S.; Ali, I.; Nawaz, Z. Rainfall prediction in Lahore City using data mining techniques. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 254–260.
Kareem, S.; Hamad, Z.J.; Askar, S. An evaluation of CNN and ANN in prediction weather forecasting: A review. Sustain. Eng. Innov. 2021, 3, 148.
Narejo, S.; Jawaid, M.M.; Talpur, S.; Baloch, R.; Pasero, E.G.A. Multi-step rainfall forecasting using deep learning approach. PeerJ Comput. Sci. 2021, 7, e514.
Elhoseiny, M.; Huang, S.; Elgammal, A. Weather classification with deep convolutional neural networks. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3349–3353.
Liu, Y.; Racah, E.; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of deep convolutional neural networks for detecting extreme weather in climate datasets. arXiv 2016, arXiv:1605.01156.
Scher, S.; Messori, G. Predicting weather forecast uncertainty with machine learning. Q. J. R. Meteorol. Soc. 2018, 144, 2830–2841.
Singhroul, A.; Agrawal, S. Artificial Neural Networks in Weather Forecasting-A Review. In Proceedings of the 2021 International Conference on Advances in Technology, Management & Education (ICATME), Bhopal, India, 8–9 January 2021; pp. 9–14.
Paras, S.M.; Kumar, A.; Chandra, M. A feature based neural network model for weather forecasting. Int. J. Comput. Intell. 2009, 4, 209–216.
Velasco, L.C.P.; Serquiña, R.P.; Zamad, M.S.A.A.; Juanico, B.F.; Lomocso, J.C. Week-ahead rainfall forecasting using multilayer perceptron neural network. Procedia Comput. Sci. 2019, 161, 386–397.
El-Shafie, A.; Noureldin, A.; Taha, M.; Hussain, A.; Mukhlisin, M. Dynamic versus static neural network model for rainfall forecasting at Klang River Basin, Malaysia. Hydrol. Earth Syst. Sci. 2012, 16, 1151–1169.
Farizawani, A.; Puteh, M.; Marina, Y.; Rivaie, A. A review of artificial neural network learning rule based on multiple variant of conjugate gradient approaches. J. Phys. Conf. Ser. 2020, 1529, 022040.
Srinu, N.; Bindu, B.H. A Review on Machine Learning and Deep Learning based Rainfall Prediction Methods. In Proceedings of the 2022 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 8–9 December 2022; pp. 1–4.
Tran, T.T.K.; Bateni, S.M.; Ki, S.J.; Vosoughifar, H. A review of neural networks for air temperature forecasting. Water 2021, 13, 1294.
Dong, Y.; Wang, J.; Xiao, L.; Fu, T. Short-term wind speed time series forecasting based on a hybrid method with multiple objective optimization for non-convex target. Energy 2021, 215, 119180.
Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668.
Dhar, D.; Bagchi, S.; Kayal, C.K.; Mukherjee, S.; Chatterjee, S. Quantitative rainfall prediction: Deep neural network-based approach. In Proceedings of International Ethical Hacking Conference 2018; Springer: Singapore, 2018; pp. 455–463.
Barman, U.; Sahu, D.; Barman, G.G. Comparison of LR, SVR, and DNN for the Rainfall Forecast of Guwahati, Assam. In Proceedings of the International Conference on Computing and Communication Systems; Springer: Singapore, 2021; pp. 297–304.
Zhang, J.; Walter, G.G.; Miao, Y.; Lee, W.N.W. Wavelet neural networks for function learning. IEEE Trans. Signal Process. 1995, 43, 1485–1497.
Estévez, J.; Bellido-Jiménez, J.A.; Liu, X.; García-Marín, A.P. Monthly precipitation forecasts using wavelet neural networks models in a semiarid environment. Water 2020, 12, 1909.
Wang, D.; Luo, H.; Grunder, O.; Lin, Y. Multi-step ahead wind speed forecasting using an improved wavelet neural network combining variational mode decomposition and phase space reconstruction. Renew. Energy 2017, 113, 1345–1358.
Venkata Ramana, R.; Krishna, B.; Kumar, S.; Pandey, N. Monthly rainfall prediction using wavelet neural network analysis. Water Resour. Manag. 2013, 27, 3697–3711.
Partal, T.; Cigizoglu, H.K.; Kahya, E. Daily precipitation predictions using three different wavelet neural network algorithms by meteorological data. Stoch. Environ. Res. Risk Assess. 2015, 29, 1317–1329.
Thuillard, M. A review of wavelet networks, wavenets, fuzzy wavenets and their applications. Adv. Comput. Intell. Learn. 2002, 18, 43–60.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Civil

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Muhammad Waqas

Usa Wannasingha Humphries

Angkool Wangwongchai

Porntip Dechpichai

Shakeel Ahmad

View Times: 378

Update Date: 01 Sep 2023

Table of Contents

Video Upload Options

Confirm