
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Vassilis C. Gerogiannis | -- | 2413 | 2023-07-25 10:59:12 | | | |
| 2 | Lindsay Dong | -92 word(s) | 2321 | 2023-07-26 02:57:40 | | |
Video Upload Options
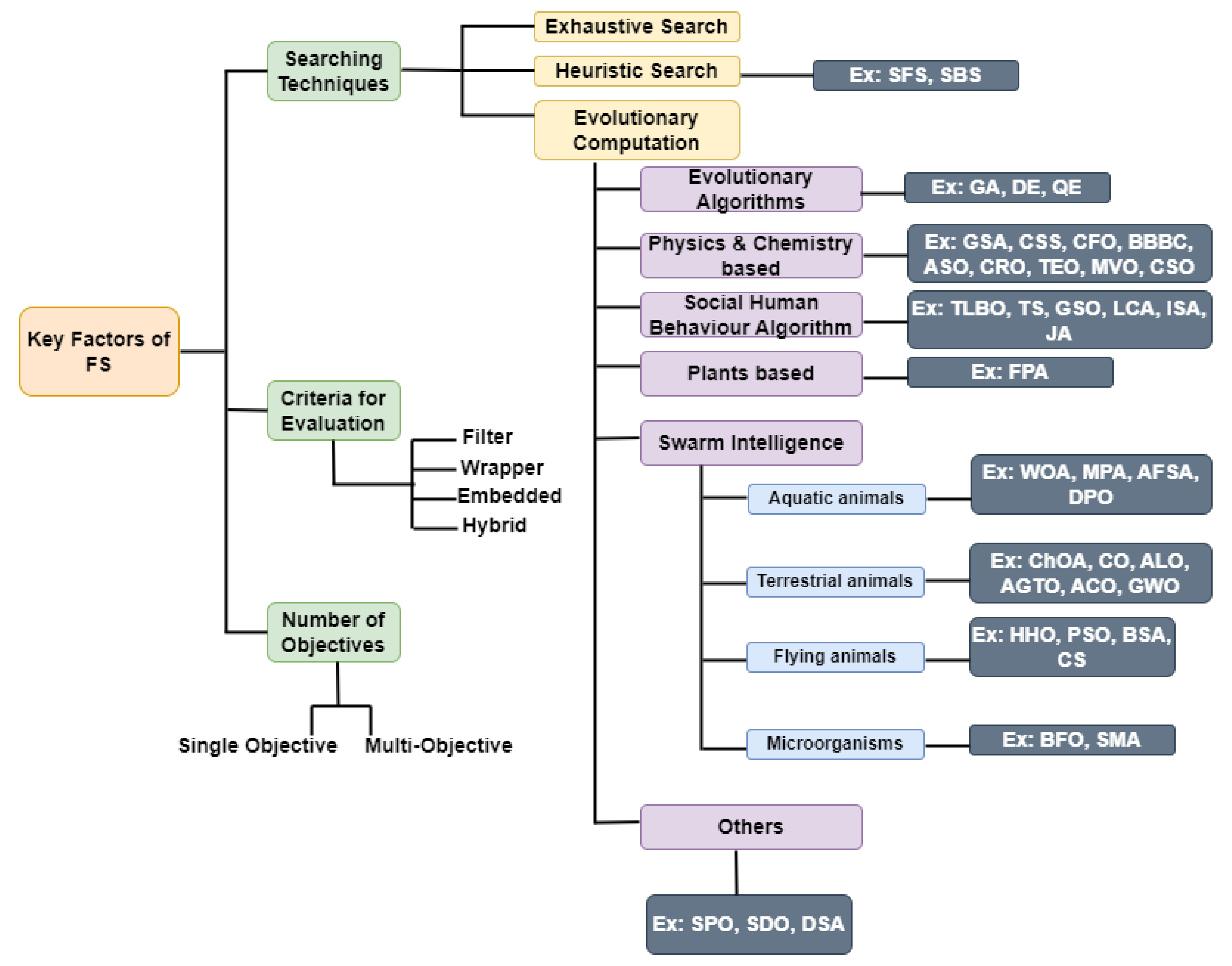
The efficiency and the effectiveness of a machine learning (ML) model are greatly influenced by feature selection (FS), a crucial preprocessing step in machine learning that seeks out the ideal set of characteristics with the maximum accuracy possible. Due to their dominance over traditional optimization techniques, researchers are concentrating on a variety of metaheuristic (or evolutionary) algorithms and trying to suggest cutting-edge hybrid techniques to handle FS issues. The use of hybrid metaheuristic approaches for FS has thus been the subject of numerous research works.
1. Introduction
2. Hybrid Evolutionary Approaches for Feature Selection
-
reducing overfitting and eliminating redundant data,
-
improving accuracy and reducing misleading results, and
-
reducing the ML algorithm training time, dropping the algorithm complexity, and speeding up the training process.
-
Genetic Algorithm (GA): A GA [43] is a metaheuristic influenced by natural selection that belongs to the larger class of evolutionary algorithms in computer science and operations research. GA relies on biologically inspired operators, such as mutation, crossover, and selection to develop high-quality solutions to optimization and search challenges. The GA is a mechanism that governs biological evolution and for tackling both constrained and unconstrained optimization issues. The GA adjusts a population of candidate solutions on a regular basis.
-
Particle Swarm Optimization (PSO): PSO is a bioinspired algorithm that is straightforward to use while looking for the best alternative in the solution space. It differs from other optimization techniques in that it simply requires the objective function and is unaffected by the gradient or any differential form of the objective. It also has a small number of hyperparameters. Kennedy and Eberhart proposed PSO in 1995 [44]. Sociobiologists think that a school of fish or a flock of birds moving in a group “may profit from the experience of all other members”, as stated in the original publication. In other words, while a bird is flying around looking for food at random, all of the birds in the flock can share what they find and assist the entire flock to get the best hunt possible.
-
Grey Wolf Optimizer (GWO): Mirjalili et al. [45] presented GWO as a new metaheuristic in 2014. The grey wolf’s social order and hunting mechanisms inspired the algorithm. First, there are four wolves, or degrees of the social hierarchy, to consider when creating GWO.–The α wolf: the solution having best fitness value;
–the β wolf: the solution having second-best fitness value;–the δ wolf: the solution having third-best fitness value; and–the ω wolf: all other solutions.As a result, the algorithm’s hunting mechanism is guided by the first three appropriate wolves, α, β, and δ. The remaining wolves are regarded as ω and follow them. Grey wolves follow a set of well-defined steps during hunting: encircling, hunting, and attacking.
-
Harris Hawk Optimization (HHO): Heidari and his team introduced HHO as a new metaheuristic algorithm in 2019 [46]. HHO uses Harris hawk principles to investigate the prey, surprise pounce, and diverse assault techniques used by Harris hawks in the environment. Hawks reflect alternatives in HHO, whereas prey represents the best solution. The Harris hawks use their keen vision to follow the target and then conduct a surprise pounce to seize the prey they have spotted. In general, HHO is divided into two phases: exploitation and exploration. The HHO algorithm can be switched from exploration to exploitation, and the exploration behaviour can then be adjusted depending on the fleeing prey’s energy.
3. Number of Objectives: Single-objective (SO) optimization frameworks are techniques which combine the classifier’s accuracy and the features quantity into a single optimization function. On the contrary, multiobjective (MO) optimization approaches entail techniques designed to find and balance the tradeoffs among alternatives. In an SO situation, a solution’s superiority over other solutions is determined by comparing the resulting fitness values, while in an MO optimization, the dominance notion is employed to get the best results [59]. In particular, to determine the significance of the derived feature sets, in an MO situation, multiple criteria need to be optimized by considering different parameters. MO strategies thus may be used to solve some challenging problems involving multiple conflicting goals [60], and MO optimization comprises fitness functions that minimize or maximize multiple conflicting goals.
References
- Piri, J.; Mohapatra, P.; Dey, R. Fetal Health Status Classification Using MOGA—CD Based Feature Selection Approach. In Proceedings of the IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; pp. 1–6.
- Bhattacharyya, T.; Chatterjee, B.; Singh, P.K.; Yoon, J.H.; Geem, Z.W.; Sarkar, R. Mayfly in Harmony: A New Hybrid Meta-Heuristic Feature Selection Algorithm. IEEE Access 2020, 8, 195929–195945.
- Piri, J.; Mohapatra, P. Exploring Fetal Health Status Using an Association Based Classification Approach. In Proceedings of the IEEE International Conference on Information Technology (ICIT), Bhubaneswar, India, 19–21 December 2019; pp. 166–171.
- Piri, J.; Mohapatra, P.; Acharya, B.; Gharehchopogh, F.S.; Gerogiannis, V.C.; Kanavos, A.; Manika, S. Feature Selection Using Artificial Gorilla Troop Optimization for Biomedical Data: A Case Analysis with COVID-19 Data. Mathematics 2022, 10, 2742.
- Jain, D.; Singh, V. Diagnosis of Breast Cancer and Diabetes using Hybrid Feature Selection Method. In Proceedings of the 5th International Conference on Parallel, Distributed and Grid Computing (PDGC), Solan, India, 20–22 December 2018; pp. 64–69.
- Mendiratta, S.; Turk, N.; Bansal, D. Automatic Speech Recognition using Optimal Selection of Features based on Hybrid ABC-PSO. In Proceedings of the IEEE International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 2, pp. 1–7.
- Naik, A.; Kuppili, V.; Edla, D.R. Binary Dragonfly Algorithm and Fisher Score Based Hybrid Feature Selection Adopting a Novel Fitness Function Applied to Microarray Data. In Proceedings of the International IEEE Conference on Applied Machine Learning (ICAML), Bhubaneswar, India, 27–28 September 2019; pp. 40–43.
- Monica, K.M.; Parvathi, R. Hybrid FOW—A Novel Whale Optimized Firefly Feature Selector for Gait Analysis. Pers. Ubiquitous Comput. 2021, 1–13.
- Azmi, R.; Pishgoo, B.; Norozi, N.; Koohzadi, M.; Baesi, F. A Hybrid GA and SA Algorithms for Feature Selection in Recognition of Hand-printed Farsi Characters. In Proceedings of the IEEE International Conference on Intelligent Computing and Intelligent Systems, Xiamen, China, 29–31 October 2010; Volume 3, pp. 384–387.
- Al-Tashi, Q.; Abdulkadir, S.J.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Approaches to Multi-Objective Feature Selection: A Systematic Literature Review. IEEE Access 2020, 8, 125076–125096.
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521.
- Venkatesh, B.; Anuradha, J. A Review of Feature Selection and Its Methods. Cybern. Inf. Technol. 2019, 19, 3–26.
- Abd-Alsabour, N. A Review on Evolutionary Feature Selection. In Proceedings of the IEEE European Modelling Symposium, Pisa, Italy, 21–23 October 2014; pp. 20–26.
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82.
- Blum, A.; Langley, P. Selection of Relevant Features and Examples in Machine Learning. Artif. Intell. 1997, 97, 245–271.
- Liu, H.; Motoda, H. Feature Selection for Knowledge Discovery and Data Mining; The Springer International Series in Engineering and Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 454.
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182.
- Piri, J.; Mohapatra, P.; Dey, R.; Panda, N. Role of Hybrid Evolutionary Approaches for Feature Selection in Classification: A Review. In Proceedings of the International Conference on Metaheuristics in Software Engineering and its Application, Marrakech, Morocco, 27–30 October 2022; pp. 92–103.
- Pudil, P.; Novovicová, J.; Kittler, J. Floating Search Methods in Feature Selection. Pattern Recognit. Lett. 1994, 15, 1119–1125.
- Mao, Q.; Tsang, I.W. A Feature Selection Method for Multivariate Performance Measures. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2051–2063.
- Min, F.; Hu, Q.; Zhu, W. Feature Selection with Test Cost Constraint. Int. J. Approx. Reason. 2014, 55, 167–179.
- Vivekanandan, T.; Iyengar, N.C.S.N. Optimal Feature Selection using a Modified Differential Evolution Algorithm and its Effectiveness for Prediction of Heart Disease. Comput. Biol. Med. 2017, 90, 125–136.
- Sahebi, G.; Movahedi, P.; Ebrahimi, M.; Pahikkala, T.; Plosila, J.; Tenhunen, H. GeFeS: A Generalized Wrapper Feature Selection Approach for Optimizing Classification Performance. Comput. Biol. Med. 2020, 125, 103974.
- Al-Tashi, Q.; Rais, H.; Jadid, S. Feature Selection Method Based on Grey Wolf Optimization for Coronary Artery Disease Classification. In Proceedings of the International Conference of Reliable Information and Communication Technology, Kuala Lumpur, Malaysia, 23–24 July 2018; pp. 257–266.
- Too, J.; Abdullah, A.R. Opposition based Competitive Grey Wolf Optimizer for EMG Feature Selection. Evol. Intell. 2021, 14, 1691–1705.
- Aghdam, M.H.; Ghasem-Aghaee, N.; Basiri, M.E. Text Feature Selection using Ant Colony Optimization. Expert Syst. Appl. 2009, 36, 6843–6853.
- Erguzel, T.T.; Tas, C.; Cebi, M. A Wrapper-based Approach for Feature Selection and Classification of Major Depressive Disorder-Bipolar Disorders. Comput. Biol. Med. 2015, 64, 127–137.
- Huang, H.; Xie, H.; Guo, J.; Chen, H. Ant Colony Optimization-based Feature Selection Method for Surface Electromyography Signals Classification. Comput. Biol. Med. 2012, 42, 30–38.
- Piri, J.; Mohapatra, P. An Analytical Study of Modified Multi-objective Harris Hawk Optimizer towards Medical Data Feature Selection. Comput. Biol. Med. 2021, 135, 104558.
- Too, J.; Abdullah, A.R.; Saad, N.M. A New Quadratic Binary Harris Hawk Optimization for Feature Selection. Electronics 2019, 8, 1130.
- Zhang, Y.; Liu, R.; Wang, X.; Chen, H.; Li, C. Boosted Binary Harris Hawks Optimizer and Feature Selection. Eng. Comput. 2021, 37, 3741–3770.
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary Ant Lion Approaches for Feature Selection. Neurocomputing 2016, 213, 54–65.
- Piri, J.; Mohapatra, P.; Dey, R. Multi-objective Ant Lion Optimization Based Feature Retrieval Methodology for Investigation of Fetal Wellbeing. In Proceedings of the 3rd IEEE International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 21–23 September 2021; pp. 1732–1737.
- Hegazy, A.E.; Makhlouf, M.A.A.; El-Tawel, G.S. Improved Salp Swarm Algorithm for Feature Selection. J. King Saud Univ.-Comput. Inf. Sci. 2020, 32, 335–344.
- Mafarja, M.M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary Dragonfly Optimization for Feature Selection using Time-varying Transfer Functions. Knowl. Based Syst. 2018, 161, 185–204.
- Sreejith, S.; Nehemiah, H.K.; Kannan, A. Clinical Data Classification using an Enhanced SMOTE and Chaotic Evolutionary Feature Selection. Comput. Biol. Med. 2020, 126, 103991.
- Das, H.; Naik, B.; Behera, H.S. A Jaya Algorithm based Wrapper Method for Optimal Feature Selection in Supervised Classification. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 3851–3863.
- Tiwari, V.; Jain, S.C. An Optimal Feature Selection Method for Histopathology Tissue Image Classification using Adaptive Jaya Algorithm. Evol. Intell. 2021, 14, 1279–1292.
- Haouassi, H.; Merah, E.; Rafik, M.; Messaoud, M.T.; Chouhal, O. A new Binary Grasshopper Optimization Algorithm for Feature Selection Problem. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 316–328.
- Mohan, A.; Nandhini, M. Optimal Feature Selection using Binary Teaching Learning based Optimization Algorithm. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 329–341.
- Dash, R. An Adaptive Harmony Search Approach for Gene Selection and Classification of High Dimensional Medical Data. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 195–207.
- Gharehchopogh, F.S.; Maleki, I.; Dizaji, Z.A. Chaotic Vortex Search Algorithm: Metaheuristic Algorithm for Feature Selection. Evol. Intell. 2022, 15, 1777–1808.
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998.
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks (ICNN), Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948.
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61.
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872.
- Liu, H.; Zhao, Z. Manipulating Data and Dimension Reduction Methods: Feature Selection. In Encyclopedia of Complexity and Systems Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 5348–5359.
- Liu, H.; Motoda, H.; Setiono, R.; Zhao, Z. Feature Selection: An Ever Evolving Frontier in Data Mining. In Proceedings of the 4th International Workshop on Feature Selection in Data Mining (FSDM), Hyderabad, India, 21 June 2010; Volume 10, pp. 4–13.
- Xue, B.; Zhang, M.; Browne, W.N. Particle Swarm Optimization for Feature Selection in Classification: A Multi-Objective Approach. IEEE Trans. Cybern. 2013, 43, 1656–1671.
- Dash, M.; Liu, H. Feature Selection for Classification. Intell. Data Anal. 1997, 1, 131–156.
- Kira, K.; Rendell, L.A. A Practical Approach to Feature Selection. In Proceedings of the 9th International Workshop on Machine Learning (ML), San Francisco, CA, USA, 1–3 July 1992; Morgan Kaufmann: Burlington, MA, USA, 1992; pp. 249–256.
- Wang, S.; Pedrycz, W.; Zhu, Q.; Zhu, W. Subspace learning for unsupervised feature selection via matrix factorization. Pattern Recognit. 2015, 48, 10–19.
- Peng, H.; Long, F.; Ding, C.H.Q. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238.
- Cervante, L.; Xue, B.; Zhang, M.; Shang, L. Binary Particle Swarm Optimisation for Feature Selection: A Filter based Approach. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Brisbane, Australia, 10–15 June 2012; pp. 1–8.
- Ünler, A.; Murat, A.E.; Chinnam, R.B. mr2PSO: A Maximum Relevance Minimum Redundancy Feature Selection Method based on Swarm Intelligence for Support Vector Machine Classification. Inf. Sci. 2011, 181, 4625–4641.
- Tan, N.C.; Fisher, W.G.; Rosenblatt, K.P.; Garner, H.R. Application of Multiple Statistical Tests to Enhance Mass Spectrometry-based Biomarker Discovery. BMC Bioinform. 2009, 10, 144.
- Tan, M.; Tsang, I.W.; Wang, L. Minimax Sparse Logistic Regression for Very High-Dimensional Feature Selection. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1609–1622.
- Zhai, Y.; Ong, Y.; Tsang, I.W. The Emerging “Big Dimensionality”. IEEE Comput. Intell. Mag. 2014, 9, 14–26.
- Thiele, L.; Miettinen, K.; Korhonen, P.J.; Luque, J.M. A Preference-Based Evolutionary Algorithm for Multi-Objective Optimization. Evol. Comput. 2009, 17, 411–436.
- Bui, L.T.; Alam, S. Multi-Objective Optimization in Computational Intelligence: Theory and Practice; IGI Global: Hershey, PA, USA, 2008.




