Quantum theory, which is focused on the physical laws that govern structures such as the nucleus of an atom or even the subatomic particles within an atomic nucleus, has properties that make it unique to most other areas of physics. Quantum theory tends to give unique, discrete energy states by defining a wave function with given boundary conditions using Erwin Schrödinger’s wave equation, helping calculate and determine the specific energy states, amongst other specific quantities this wave function would be likely to have. Quantum theory disconnects itself from the normal classical theories of physics in that it does not treat variables along a continuous spectrum, but rather finds discrete states which these variables can be expected to have.
1. Introduction
The field of medicine is unique in that different area of the world employ different ideologies and have different approaches to treat, cure, and prevent disease amongst their populations. The actual practice of medicine has been around for centuries, but as civilizations grew and expansion across the world occurred, new cultures arose, and consequently new viewpoints and belief systems came into existence. In turn, the way medicine has been approached by different cultures has been unique to those respective societies. In addition to this, as education expanded and technological innovations continued to develop, new processes, advancements, and breakthroughs in the field of science came about, and the field of medicine inherently changed as well. Medicine is so amazing in that it uses the field of science to help treat individuals for a myriad of different diseases and health-related issues. When people think about medicine in the modern twenty-first century, some fields that come to mind are biology and chemistry, which makes sense. Biology is defined as the structure of living organisms, and medicine is all about treating the human body. Chemistry studies reactions between different molecules and hence is one of the foundational subjects for helping develop drugs and different treatments for a multitude of diseases in medicine. However, there has been a growing and substantiated interest in integrating quantum mechanics and quantum theory—both subsections of quantum physics—into medicine. Quantum physics is a branch of science that focuses on quantum mechanics and stems from quantum theory; quantum mechanics is the unique set of principles that explain the behavior of matter and energy that can in turn help explain quantum theory. Quantum physics is unique from most classical applications of physics in that it focuses on the physical properties of subatomic and fundamental particles, focusing on the micro-scale at the most extreme of levels, which classical physics does not achieve. New quantum technology and applications in the clinical sciences have demonstrated that understanding quantum mechanics can pose great benefits in learning more about cancer, telomere reduction, and the neurological framework of the human brain. In addition to this, applying quantum theory in medicine can allow for a much better understanding of DNA changes under mutagenesis, and can even help increase the rate at which diseases are diagnosed, even before symptoms arise in a patient. The intersectionality between the fields of quantum physics and medicine can facilitate a greater understanding of how certain diseases arise, and therefore help patients in future treatment. Hence, scientists in the field of medicine, as well as those in the field of quantum physics, have begun to realize that these two fields actually have more to do with one another than people usually realize, and it is worth delving into the intersectionality between these two fields and bringing them together as a means of advancing the field of medicine through unique applications in quantum theory.
2. Application of Quantum Theory in the Mind and Neurological Network Transmissions
Certain research has delved into the consciousness of the human species as a means of understanding how our thought processes, thinking styles, and cognitive behavior relates to neuroanatomy and even in the goals of helping combat certain diseases. For instance, studies on the ability of human consciousness to adapt in different situations, such as under anesthesia during surgery, or even studies on the general changes in consciousness when an individual begins to develop diseases such as Alzheimer’s disease, are extremely important because it can affect their decision-making skills and ability to act, even in a medical context
[1]. Thus, learning how consciousness can be affected by drugs like anesthetics or even how it is affected by a neurodegenerative disease is extremely important in the field of medicine, as these can all affect a patient’s ability to perform daily tasks and not feel pain during a medical procedure. However, research in the field of physics has found that classical mechanics is not constitutionally suited to accommodate consciousness based on certain mathematical characteristics, whereas quantum mechanics is. The nature of the information represented in the state of the brain, and the way this information enters the dynamics, is attributed to these mathematical characteristics
[2]. Quantum mechanics is uniquely differentiable from classical mechanics in that, as previously described, the former relies on equations that help describe characteristics of a wave function and focuses on discrete probable states rather than a continuous spectrum. The mathematics employed in quantum physics is more akin to the statistical variety, whereas classical physics is more definitive and focused on exact, definitive answers for certain physical quantities. Neither is more right or wrong than the other; rather, they both just answer different types of questions. In the area of human consciousness, specifically with the ability of the brain to transmit signals and information and the structure of the neurological system of the human body, it has been found that the field of quantum theory actually holds great promise in helping us understand these underlying mechanisms.
Further research has focused on ways to use quantum mechanics as a means of describing certain decision-making processes and behaviors, which can help advance specific fields of medicine that deal with decision-making and overall consciousness, such as in the brain with neurology and even with sedatives such as in anesthesiology, as described earlier. Physicists and mathematicians have tried relying on quantum-state reductions as a means of helping describe conscious interpretation by the human brain. The exact definition of a quantum-state reduction is that it “is the state change of the measured system caused by a measurement conditional upon the outcome of the measurement, [and] is developed fully within quantum mechanics”
[3]. In practical terms, however, the simple mechanism of these quantum-state reductions is to help describe the behavior of how things are inevitably perceived by conscious understanding. Quantum-state reductions are critical to understanding the human mind and consciousness because, as a conscious decision is determined and neurological networks transmit this information, it can be physically represented with wave function collapsing. These quantum-state reductions are critical because they can provide a physical understanding of how neurological transmission occurs and how things are perceived by the consciousness, something which is extremely pertinent for neurology and the overall field of medicine. Described simply, “Consciousness and reality are related through the ‘measurement problem’ in quantum mechanics, i.e., why we do not consciously perceive particles as quantum superpositions of multiple possibilities, as they appear to be when unobserved, but rather perceive them consciously as being in definite states or locations”
[4]. Mathematically, the goal of quantum-state reductions is to collapse the wave function or take a multitude of differing eigenstates and produce only one final eigenstate after there is some interaction or measurement with the external environment.
When analyzing the quantum theory behind this proposal, John von Neumann argued that one could use a projection postulate to help describe these so-called measurements, treating them as instantaneous and irreversible actions
[5], using the following quantum formulization to describe how the wave function collapses (or in general, how a singular definitive conscious interpretation is reached in the brain with its final eigenstate):
where “
H” is the Hamiltonian operator, “
p” is the state of the system before measurement, and “
𝑈𝑡” is the unitary time evolution operator. Henry Stapp used the groundwork von Neumann provided for these quantum-state reductions and purported that the boundary between these observed and observing systems mathematically described through this quantum representation is actually located in the human brain, and even further argued that quantum uncertainties at the level of the synapse can actually generate effects that are big enough to allow for superpositions of macroscopic brain activity, which occurs at the level of neuronal assemblies. This posited theory by Staff, taking from the mathematical basis of von Neumann, could have enormous implications for the field of medicine. If one uses this quantum theory to describe how neuronal assembly occurs in relation to how conscious behavior reaches a singular final state when interacting with an external stimulus, this could help describe certain changes in neural activity when a patient develops a neurodegenerative disease like Alzheimer’s disease. Moreover, finding the underlying mechanisms behind how anesthetics can inhibit conscious activity can be mathematically mapped out using these quantum projections, analyzing the process by which the final eigenstate is reached once these drugs are administered into the human body. It is an extremely fascinating theory, but more concrete research, evidence, and further experimentation are needed before this quantum application can be medically applied. Nonetheless, this demonstrates that the field of quantum physics has a lot more to offer in the field of medicine than people may have initially expected.
In general, quantum-state reductions can be explained through von Neumann’s work on consciousness and neuronal assemblies. Von Neumann’s work explains the conceptual distinction between an observed and observing system. Defining a measured object system (I), a measuring instrument (II), and the brain of a human observer (III), von Neumann found that it makes no difference whether the boundary between the observed and observing systems is posited between I and (II and III) or between (I and II) and III for the result of measurements on (I). This result is extremely profound, as this means that it is not significant whether a detector or the human brain is ultimately referred to as the “observer”. When analyzing the so-called collapse of a wave function, von Neumann’s work reveals that these irreversible actions could possibly hold significance in explaining conscious decision-making processes. Conscious decision-making behavior is a process that could indeed be described through these quantum-state reductions, where wave functions collapse and results are irreversible, as opposed to the continuous and reversible changes in a system according to the Schrödinger equation
[6]. In turn, incorporating quantum theory into the field of medicine, and in the field of neurology, can help us reach a better understanding of how neural networks change over time in individuals with neurodegenerative diseases like Alzheimer’s, where conscious decision-making processes can be altered or weakened.
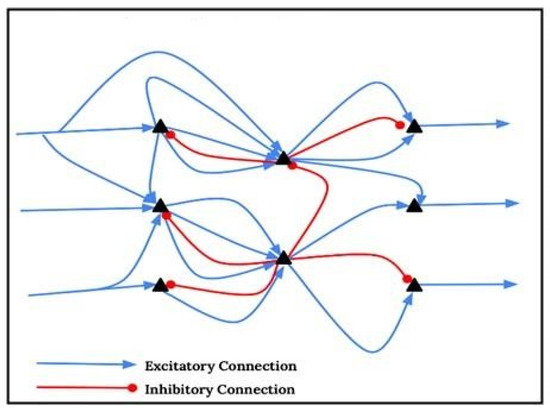
The neural assemblies of the brain can be described through both excitatory and inhibitory connections. A fair question to ask is whether there is a “neural correlate” for mental representation. In fact, the neural correlate of a mental representation can be characterized by the fact that the connectivity or coupling among those neurons form an assembly confined with respect to its environment, to which connectivity is weaker than within the assembly
[6]. Thus, the neural correlation of a mental representation is activated if the neurons which form the assembly itself operate more actively by, e.g., producing higher firing rates than when in their normal mode. To maintain a stable operation of an activated neuronal assembly, there must be an equilibrium between the inhibitory and the excitatory connections amongst the neurons (see
Figure 1). If the transfer function of individual neurons is strictly monotonic (which means increasing input leads to increasing output), assemblies will be difficult to stabilize, and equilibrium cannot be maintained. Therefore, the goal is to have results establishing a non-monotonic transfer function with a maximal output at intermediate input; this is of high significance for the modeling of neuronal assemblies
[7]. Yet, mathematically, network models using lattices of coupled maps with a quadratic maximum are paradigmatic examples of this exact behavior, which is extremely beneficial
[8]. Thus, incorporating these different network models, which are very similar to ideas described in quantum theory, where conscious decision making comes from collapsing wave functions and reaching one final irreversible state, can have great benefit in explaining certain biological phenomena, bringing an intersectionality between the two fields of quantum mechanics and medicine.
Figure 1. Equilibrium between neurons.
There are some concerns and controversies regarding applying quantum theory to the mind and neurological network transmissions. The general use of measurement that von Neumann describes—conscious decision making with collapsing wave functions—relies on certain principles that are in contention. The overall act of measurement is an essential aspect in the framework of quantum theory that has been the subject of controversy for more than eight decades now. In addition to this, there are other features of quantum theory which became attractive when discussing issues of consciousness, such as the concepts of complementarity and entanglement. Physicists such as Planck, Bohr, Schrödinger, and Pauli who helped lay the foundation for quantum theory focused on the various possible roles of quantum theory in reconsidering the “old conflict between physical determinism and conscious free will”. In turn, this new branch of physics did not necessarily always complement and agree with the previously utilized classical form of physics where energy was viewed as a continuous quantity. In turn, there is debate over whether fully relying on quantum theory to not only explain the neurological framework of the human body but also decision making is truly the most reliable approach. However, there is growing support and evidence as research continues to expand that demonstrates how the theories in the field of quantum physics do hold promise for helping us better understand how decision-making processes in the brain can be described.