Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Ya-Zhou Shi
 -- 2098 2023-06-27 12:14:14 |
2 layout
Jessie Wu
 + 4 word(s) 2102 2023-06-28 04:44:04 | |
3 layout
Jessie Wu
 -3 word(s) 2099 2023-06-28 04:45:10 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Mu, Z.; Tan, Y.; Liu, J.; Zhang, B.; Shi, Y. Molecular Dynamics Simulations for DNAs. Encyclopedia. Available online: https://encyclopedia.pub/entry/46114 (accessed on 29 April 2024).
Mu Z, Tan Y, Liu J, Zhang B, Shi Y. Molecular Dynamics Simulations for DNAs. Encyclopedia. Available at: https://encyclopedia.pub/entry/46114. Accessed April 29, 2024.
Mu, Zi-Chun, Ya-Lan Tan, Jie Liu, Ben-Gong Zhang, Ya-Zhou Shi. "Molecular Dynamics Simulations for DNAs" Encyclopedia, https://encyclopedia.pub/entry/46114 (accessed April 29, 2024).
Mu, Z., Tan, Y., Liu, J., Zhang, B., & Shi, Y. (2023, June 27). Molecular Dynamics Simulations for DNAs. In Encyclopedia. https://encyclopedia.pub/entry/46114
Mu, Zi-Chun, et al. "Molecular Dynamics Simulations for DNAs." Encyclopedia. Web. 27 June, 2023.
Molecular Dynamics Simulations for DNAs
Edit
This entry is adapted from the peer-reviewed paper 10.3390/molecules28124833

DNA carries the genetic information required for the synthesis of RNA and proteins and plays an important role in many processes of biological development. Understanding the three-dimensional (3D) structures and dynamics of DNA is crucial for understanding their biological functions and guiding the development of novel materials. Molecular dynamics (MD) simulations can generally reproduce the behavior of DNAs in a computer, providing detailed structural and dynamical insights that enhancing our comprehension of relevant experimental data. MD simulations using classical force fields such as AMBER and CHARMM have provided highly detailed and flexible descriptions of DNA dynamics, including structural transformations, stability of non-canonical conformations, salt ion cohesion effects, twist-stretch coupling of stress, flexibility under methylation modifications, and interactions with other macromolecules. It is always fascinating to obtain microscopic insights into DNA dynamics through MD simulations. However, the innumerable degrees of freedom, interconnected in complex ways, can make it practically impossible to detect DNA dynamics on biologically relevant time scales and length scales using currently available computer hardware

DNA 3D structures computational modeling molecular dynamics simulations

1. Introduction

Molecular dynamics (MD) simulations of DNA systems are typically performed by calculating the force on each atom as a function of their positions using all-atomic force fields (such as AMBER, CHARMM, GROMOS, and OPLS) (Figure 1a). These force fields are parameterized using experiments or quantum chemistry calculations of small systems [1][2][3][4][5][6]. CHARMM36 [3] and AMBER ff99bsc1 [6], which have been validated and improved through multiple revisions, are commonly used for DNA simulations. Although these force fields have limitations, such as AMBER potentially overestimating base stacking effects and CHARMM weakening base pairing [7][8], they have been successfully employed to simulate DNA systems, providing atomistic resolution and establishing quantitative relationships between structure and conformational energy [9][10].
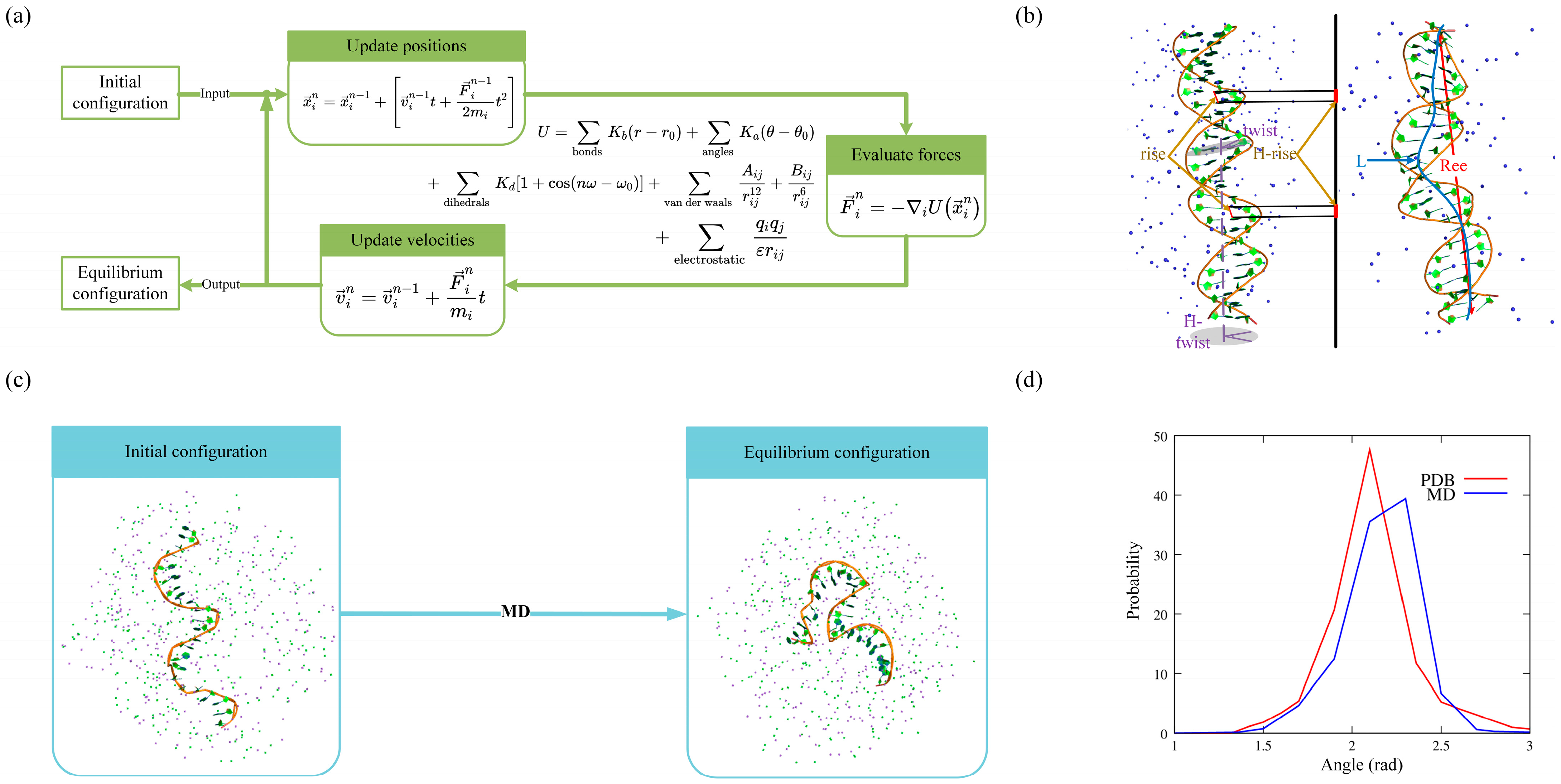
Molecules 28 04833 g002 550
Figure 1. (a) Schematic diagram of MD simulations. (b) Diagram of calculations on the flexibility of dsDNA in MD simulations. Left: initial conformation. Right: equilibrium conformation. (c) MD simulations for short ssDNA in ion solutions. (d) Distributions of the angle between contiguous P-C4′-P atoms from experimental structures (red) and MD simulated conformations (blue). The three-dimensional (3D)f structures are shown with PyMol (http://www.pymol.org).

2. Structural Dynamics

MD simulations have been effective in accurately probing the atomic motions and structural dynamics of DNAs [11][12][13][14][15][16][17][18], enabling researchers to understand the DNA functions. To address the question of how long an MD simulation of a B-DNA helix needs to be to sample the dominant structural and dynamical features, Galindo-Murillo et al. presented an extensive analysis using multiple μs-length MD simulations of a dsDNA (d(GCACGAACGAACGAACGC)) with Amber 14 and a ff99SB parmbsc0 or CHARMM C36 force field on multiple computer architectures (including Anton, CPU, and GPU). The results showed that despite the underlying differences in hardware, the simulations performed on different architectures exhibited minimal structural variation with respect to one another. These MD simulations, including the longest one at ~44 μs, also suggested that the structure and dynamics of the DNA helix, excluding the terminal base pairs, reach near-full convergence on the ~1–5 μs timescale. This indicates that the current force field is reasonably robust. However, the convergence of the terminal base pair opening events occurs on time scales significantly longer than 10 μs and cannot be fully captured through ensembles of shorter and independent MD simulations [19][20]. In a separate study, Yang et al. performed umbrella MD simulations of A-T sequence-rich B-DNA using the Amber force field and reproduced the experimental conformational transition path from Watson–Crick to Hoogsteen base pairs observed in NMR relaxation dispersion spectroscopy [21]. This indicates that MD simulations have the power to describe large-scale structural dynamics at short timescales using an advanced-sampling approach [22].
In addition, MD simulations can also provide detailed insight into DNA structure dynamics. For example, Chakraborty et al. employed the AMBER12 package and Joung/Cheatham ion parameters to explore the transition between B- and Z-dsDNAs. Their study found that the free energy landscape exhibits two distinct funnels, leading to the B-DNA and Z-DNA conformations. This suggests that the reversal of chirality is caused by the stretched DNA structure or mutual competition at the B–Z junction [23].

3. Structural Flexibility

In recent years, MD simulations have been widely used to study the flexibility of DNAs, as DNA structural flexibility is closely associated with many biological processes involving the storage or encoding of genetic information [24][25]. Although many results from single-molecule experiments can be well-described by the commonly accepted WLC models [26][27][28], atomistic MD simulations are extensively used to obtain microscopic descriptions of DNA flexibility, such as the width and depth of the major/minor grooves and the distances/twist angles between neighbor base pairs [29][30][31]. For example, to explain the experimental results that short DNAs consisting of tens of base pairs (bps) may have seemingly higher flexibility than those of kilobase pairs, Wu et al. performed MD simulations for short dsDNAs with a finite-length of 5–50 bps using the Amber parmbsc0 force field. Their microscopic analyses (the calculation of stretching and bending at the base-pair level) revealed that the apparent high flexibility of short dsDNAs arises from significantly strong bending and stretching flexibilities at each helix end, consisting of ∼6 bps [32]. In addition to the length-dependent flexibility of DNA, Marin-Gonzalez et al. performed over 1μs-long constant-force MD simulations of 18 bp-long dsDNAs (CGCG(NN)5CGCG, with NN as the AA, AC, AG, AT, CG, and GG). They found that the DNA crookedness (a sequence-dependent deformation of DNA that consists of periodic bends in the chain of base pair centers) and its associated flexibility can regulate DNA mechanical properties at short length scales. This unveiled a one-to-one relation between DNA structure and dynamics [33]. To understand the distinct differences in the flexibility of dsRNA and dsDNA helices, Liebl et al. performed unrestrained/restrained MD simulations for a 16 bp dsDNA or dsRNA using the AMBER12 package with the parmbsc0 force field. Their detailed analysis of helical deformations, coupled with twist, indicated that the interplay of helical rise, base pair inclination, and displacement from the helix axis during twist changes is responsible for the different twist–stretch correlations [34]. Coincidentally, Marin-Gonzalez et al. investigated the difference between dsDNA and dsRNA (16 bp) using microsecond-long MD simulations under constant stretching forces within the range of 1–20 pN. They showed that the opposite twist–stretch coupling of both molecules is due to the markedly different evolution of inter-strand distance with the stretching force, which is directly correlated with the slide base-pair parameter and sugar pucker angle [35]. Recently, Bao et al. also conducted extensive MD simulations for larger dsDNA and dsRNA (40 bp) without applying stretch force, using the AMBER ff99bsc0 force field. Their work provides a more quantitative understanding of the relative flexibility of dsRNA and dsDNA in terms of both stretching and twist–stretch coupling. They noted that the striking difference in twist–stretch coupling between dsRNA and dsDNA is attributed to the apparently stronger base-pair inclination in dsRNA compared to dsDNA (Figure 1b) [36].
In addition, MD simulations can be used to reproduce the effect of base modifications or base-pair mutations on DNA flexibility [37][38]. For example, Aksimentiev et al. combined MD simulations (using the NAMD program with a CHARMM36 force field) with a single-molecule cyclization assay to study how different cytosine modifications influence the physical properties of dsDNA (70 bp). They elucidated the microscopic mechanisms behind the changes in DNA flexibility induced by cytosine modifications: these modifications can promote or dampen structural fluctuations through the competing effects of base polarity and steric hindrance [39]. Given that the appearance of mismatched base pairs (MMs) can result in the development of inherited genetic diseases, cancer, and aging, Rossetti et al. presented the first comprehensive study on the structure of MM-containing DNA duplexes (12 MMs, including A·A, A·C, A·G, C·A, C·C, C·T, G·A, G·G, G·T, T·C, T·G, and T·T, placed in the center of 13 bp duplexes, e.g., d(CCATACXATACGG)). They employed MD simulations (Gromacs v.4.5.5 program with parmbsc0 force field) and NMR spectroscopy and found that the presence of mismatches produced significant local structural alterations due to the flexible MMs (especially in the case of purine transversions). These alterations could be propagated far from the mismatch site, influencing the global structures of DNA [40]. On the other hand, Bouchal et al. also employed MD simulations (Amber 16 package with parmbsc1 force field) to calculate the thermodynamic stabilities of MMs in similar dsDNAs (e.g., d(GGTTAAXTTAACC) with anti/anti, anti/syn, and syn/anti MM combinations) as a function of two geometry parameters of the base pair (opening and shear). However, their detailed analysis showed that there was no clear dissection between the canonical and mismatched base pairs [41]. This discrepancy suggests that MD simulations may be less credible in capturing the local sequence effects on DNA flexibility [36] due to the empirical force field.

4. DNA–Ion Interaction

Since DNA is an anionic polyelectrolyte, the solvent environment plays a significant role in DNA structures [42][43][44][45][46]. Pasi et al. performed microsecond MD simulations for 39 dsDNAs (with a length of 18 bp and different sequences) under physiological salt conditions using the parmbsc0 force field with Dang parameters for the ions. They provided a comprehensive state-of-the-art perspective on sequence-dependent potassium ion populations. For example, they observed that potassium ions within the grooves are more likely to accumulate around electronegative base sites rather than the anionic phosphate groups [47]. Considering the experimental results showing that high-valent cation can lead to the opposite effect on the elasticities of DNA and RNA duplexes, Fu et al. used MD simulations for 20 bp dsDNA and dsRNA in trivalent ion solutions (i.e., CoHex3+). They found that these results were caused by different binding modes of the cations on dsDNA and dsRNA [48]. More recently, Cruz-Leon et al. also combined high-resolution MT experiments with MD simulations (parmbsc1 force field on 33 bp dsDNA) to show that increasing ion concentration leads to a decrease in helical radius and crookedness, an increase in sugar pucker, and ultimately an increase in a twist. This is due to the increased screening of electrostatic repulsion between phosphate groups [49].
Furthermore, MD can provide an atomistic understanding of how DNA–ion interactions vary with different metal ions (Figure 1b,c). For example, Long et al. performed MD simulations to sample the structures of a 23 bp DNA duplex in various ion solutions (such as Mg2+, Ca2+, Sr2+, or Ba2+). They demonstrated that these ions exhibit a preference for binding to the phosphate backbone rather than the major groove [50]. To investigate the competitive binding of divalent and monovalent ions to dsDNA, Xi et al. performed all-atom MD simulations for a 24 bp dsDNA in mixed Mg2+/Na+ solutions using the Amber parmbsc0 force field with Joung/Cheatham ion model for Na+/Cl− and the Aqvist ion model for Mg2+. Their comprehensive analysis suggested that the global binding of Mg2+ over Na+ to nucleic acids is primarily dependent on the surface charge density and Mg2+/Na+ concentrations [51].

5. Limitations

In the last 40 years, MD simulations have made significant progress in providing atomistic insights into DNA structures, including dynamics, flexibility, and ion binding. Although recent efforts combining experiments and simulations show promise for improving the accuracy of nucleic acid force fields, MD simulations are not always effective, particularly for ssDNAs [52][53]. Recently, researchers performed MD simulations for unstructured ssDNA (with a random sequence: 5′-CTGCCACGCCATGCCTGTGACGA-3′ at 1 M [Na+]) and tried to extract the bonded parameters from the equilibrium conformations. However, researchers found that the distributions of several angles in MD conformations deviated from those observed in PDB structures. For example, the P-C4′-P angle showed a deviation of ~11° from its optimal value, as shown in Figure 1d. In addition, the ion parameters, which are optimized based on a set of experimental solution properties such as solvation-free energies, radial distribution functions, water exchange rates, and activity coefficient derivatives, could be limited in their transferability to quantitatively describe biomolecular systems [54][55]. Thus, further investigations of diverse DNA structures (e.g., ssDNA, pseudoknots, G-quadruplexes, i-motifs, and DNA complexes) in ion solutions are needed to further assess the quality of these force fields [52][53][56][57].
Furthermore, MD simulations in equilibrium are not always adequate to sufficiently explore the structural space needed for accurate property estimation [58][59]. In MD simulations, the initial conformation is usually established based on an experimentally known structure. If the molecule acquires another stable conformation that is separated by a high free energy barrier, the system’s acquisition of this alternative conformation within a realistic computational cost becomes challenging due to the barrier [53]. Finally, sampling remains an issue in some nucleic acid simulations, thus requiring the extension of simulation time scales and exploration of efficient enhanced sampling methods (e.g., temperature replica exchange, Hamiltonian and multi-dimensional replica exchange, metadynamics, and umbrella sampling). These efforts are important for future advancements [60][61][62].

References

  1. Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2005, 26, 114.
  2. Zhang, Y.; Zhang, Y.; McCready, M.J.; Maginn, E.J. Evaluation and refinement of the general AMBER force field for nineteen pure organic electrolyte solvents. J. Chem. Eng. 2018, 3488–3502.
  3. Hart, K.; Foloppe, N.; Baker, C.M.; Denning, E.J.; Nilsson, L.; MacKerell, A.D., Jr. Optimization of the CHARMM additive force field for DNA: Improved treatment of the BI/BII conformational equilibrium. J. Chem. Theory Comput. 2012, 8, 348–362.
  4. Scott, W.R.P.; Hünenberger, P.H.; Tironi, I.G.; Mark, A.E.; Billeter, S.R.; Fennen, J.; Torda, A.E.; Huber, T.; Kruger, P.; Van Gunsteren, W.F. The GROMOS biomolecular simulation program package. J. Phys. Chem. 1999, 103, 3596–3607.
  5. Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509.
  6. Ivani, I.; Dans, P.D.; Noy, A.; Pérez, A.; Faustino, I.; Hospital, A.; Walther, J.; Andrio, P.; Goñi, R.; Balaceanu, A.; et al. Parmbsc1: A refined force field for DNA simulations. Nat. Methods 2016, 13, 55–58.
  7. Chen, A.A.; García, A.E. High-resolution reversible folding of hyperstable RNA tetraloops using molecular dynamics simula-tions. Proc. Natl. Acad. Sci. USA 2013, 110, 16820–16825.
  8. Gallardo, A.; Bogart, B.M.; Dutagaci, B. Protein–Nucleic Acid Interactions for RNA Polymerase II Elongation Factors by Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 3079–3089.
  9. Salsbury, A.M.; A Lemkul, J. Recent developments in empirical atomistic force fields for nucleic acids and applications to studies of folding and dynamics. Curr. Opin. Struct. Biol. 2021, 67, 9–17.
  10. Kameda, T.; Awazu, A.; Togashi, Y. Molecular dynamics analysis of biomolecular systems including nucleic acids. Biophys. Physicobiology 2022, 19, e190027.
  11. Ghoshdastidar, D.; Bansal, M. Dynamics of physiologically relevant noncanonical DNA structures: An overview from experi-mental and theoretical studies. Brief. Funct. Genom. 2018, 18, 192–204.
  12. Frank-Kamenetskii, M.D.; Prakash, S. Fluctuations in the DNA double helix: A critical review. Phys. Life Rev. 2014, 11, 153–170.
  13. Zgarbová, M.; Šponer, J.; Otyepka, M.; Cheatham, T.E., III; Galindo-Murillo, R.; Jurečka, P. Refinement of the Sugar–Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA. J. Chem. Theory Comput. 2015, 11, 5723–5736.
  14. Strelnikov, I.A.; Kovaleva, N.A.; Klinov, A.P.; Zubova, E.A. C-B-A test of DNA force fields. ACS Omega 2023, 8, 10253–10265.
  15. Panczyk, T.; Wojton, P.; Wolski, P. Mechanism of unfolding and relative stabilities of G-quadruplex and I-motif noncanonical DNA structures analyzed in biased molecular dynamics simulations. Biophys. Chem. 2019, 250, 106173.
  16. Panczyk, T.; Wojton, P.; Wolski, P. Molecular Dynamics Study of the Interaction of Carbon Nanotubes with Telomeric DNA Fragment Containing Noncanonical G-Quadruplex and i-Motif Forms. Int. J. Mol. Sci. 2020, 21, 1925.
  17. Liu, T.; Yu, T.; Zhang, S.; Wang, Y.; Zhang, W. Thermodynamic and kinetic properties of a single base pair in A-DNA and B-DNA. Phys. Rev. E 2021, 103, 042409.
  18. Xu, S.; Zhan, J.; Man, B.; Jiang, S.; Yue, W.; Gao, S.; Guo, C.; Liu, H.; Li, Z.; Wang, J.; et al. Real-time reliable determination of binding kinetics of DNA hybridization using a multi-channel graphene biosensor. Nat. Commun. 2017, 8, 14902.
  19. Galindo-Murillo, R.; Roe, D.R. Cheatham TE 3rd. On the absence of intrahelical DNA dynamics on the μs to ms timescale. Nat. Commun. 2014, 5, 5152.
  20. Galindo-Murillo, R.; Roe, D.R.; Cheatham, T.E. Convergence and reproducibility in molecular dynamics simulations of the DNA duplex d(GCACGAACGAACGAACGC). Biochim. Biophys. Acta 2015, 1850, 1041–1058.
  21. Nikolova, E.N.; Kim, E.; Wise, A.A.; O’brien, P.J.; Andricioaei, I.; Al-Hashimi, H.M. Transient Hoogsteen base pairs in canonical duplex DNA. Nature 2011, 470, 498–502.
  22. Yang, C.; Kim, E.; Pak, Y. Free energy landscape and transition pathways from Watson–Crick to Hoogsteen base pairing in free duplex DNA. Nucleic Acids Res. 2015, 43, 7769–7778.
  23. Chakraborty, D.; Wales, D.J. Probing helical transitions in a DNA duplex. Phys. Chem. Chem. Phys. 2017, 19, 878.
  24. Marin-Gonzalez, A.; Vilhena, J.G.; Perez, R.; Moreno-Herrero, F. A molecular view of DNA flexibility. Q. Rev. Biophys. 2021, 54, e8.
  25. Ghoshdastidar, D.; Bansal, M. Flexibility of flanking DNA is a key determinant of transcription factor affinity for the core motif. Biophys. J. 2022, 121, 3987–4000.
  26. Nomidis, S.K.; Kriegel, F.; Vanderlinden, W.; Lipfert, J.; Carlon, E. Twist-Bend Coupling and the Torsional Response of Double-Stranded DNA. Phys. Rev. Lett. 2017, 118, 217801.
  27. Marko, J.F.; Siggia, E.D. Fluctuations and Supercoiling of DNA. Science 1994, 265, 506–508.
  28. Toan, N.M.; Thirumalai, D. On the origin of the unusual behavior in the stretching of single-stranded DNA. J. Chem. Phys. 2012, 136, 235103.
  29. Qiang, X.-W.; Dong, H.-L.; Xiong, K.-X.; Zhang, W.; Tan, Z.-J. Understanding sequence effect in DNA bending elasticity by molecular dynamic simulations. Commun. Theor. Phys. 2021, 73, 075601.
  30. Liebl, K.; Dršata, T.; Lankas, F.; Lipfert, J.; Zacharias, M. Explaining the striking difference in twist-stretch coupling between DNA and RNA: A comparative molecular dynamics analysis. Nucleic Acids Res. 2015, 43, 10143–10156.
  31. Chen, C.; Pettitt, B.M. The Effects of Flexibility on dsDNA-dsDNA Interactions. Life 2022, 12, 699.
  32. Wu, Y.-Y.; Bao, L.; Zhang, X.; Tan, Z.-J. Flexibility of short DNA helices with finite-length effect: From base pairs to tens of base pairs. J. Chem. Phys. 2015, 142, 125103.
  33. Marin-Gonzalez, A.; Vilhena, J.G.; Moreno-Herrero, F.; Perez, R. DNA Crookedness Regulates DNA Mechanical Properties at Short Length Scales. Phys. Rev. Lett. 2019, 122, 048102.
  34. Liebl, K.; Zacharias, M. Accurate modeling of DNA conformational flexibility by a multivariate Ising model. Proc. Natl. Acad. Sci. USA 2021, 118, e2021263118.
  35. Marin-Gonzalez, A.; Vilhena, J.G.; Perez, R.; Moreno-Herrero, F. Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics. Proc. Natl. Acad. Sci. USA 2017, 114, 7049–7054.
  36. Bao, L.; Zhang, X.; Shi, Y.-Z.; Wu, Y.-Y.; Tan, Z.-J. Understanding the Relative Flexibility of RNA and DNA Duplexes: Stretching and Twist-Stretch Coupling. Biophys. J. 2017, 112, 1094–1104.
  37. Bouchal, T.; Durník, I.; Kulhánek, P. Bending of Canonical and G/T Mismatched DNAs. J. Chem. Inf. Model. 2021, 61, 6000–6011.
  38. Sharma, M.; Predeus, A.V.; Mukherjee, S.; Feig, M. DNA Bending Propensity in the Presence of Base Mismatches: Implications for DNA Repair. J. Phys. Chem. B 2013, 117, 6194–6205.
  39. Maffeo, C.; Ngo, T.T.M.; Ha, T.; Aksimentiev, A. A Coarse-Grained Model of Unstructured Single-Stranded DNA Derived from Atomistic Simulation and Single-Molecule Experiment. J. Chem. Theory Comput. 2014, 10, 2891–2896.
  40. Rossetti, G.; Dans, P.D.; Gomez-Pinto, I.; Ivani, I.; Gonzalez, C.; Orozco, M. The structural impact of DNA mismatches. Nucleic Acids Res. 2015, 43, 4309–4321.
  41. Bouchal, T.; Durník, I.; Illík, V.; Réblová, K.; Kulhánek, P. Importance of base-pair opening for mismatch recognition. Nucleic Acids Res. 2020, 48, 11322–11334.
  42. Lavery, R.; Maddocks, J.H.; Pasi, M.; Zakrzewska, K. Analyzing ion distributions around DNA. Nucleic Acids Res. 2014, 42, 8138–8149.
  43. Tolokh, I.S.; Thomas, D.G.; Onufriev, A.V. Explicit ions/implicit water generalized Born model for nucleic acids. J. Chem. Phys. 2018, 148, 195101.
  44. Sun, L.Z.; Qian, J.L.; Cai, P.; Xu, X. Mutual effects between single-stranded DNA conformation and Na+-Mg2+ ion competition in mixed salt solutions. Phys. Chem. Chem. Phys. 2022, 24, 20867–20881.
  45. Xue, J.; Wang, P.; Li, X.; Tan, R.; Zong, W. Transformation characteristics of A-DNA in salt solution revealed through molecular dynamics simulations. Biophys. Chem. 2022, 288, 106845.
  46. Sarkar, S.; Singh, P.C. The combined action of cations and anions of ionic liquids modulates the formation and stability of G-quadruplex DNA. Phys. Chem. Chem. Phys. 2021, 23, 24497–24504.
  47. Pasi, M.; Maddocks, J.H.; Lavery, R. Analyzing ion distributions around DNA: Sequence-dependence of potassium ion distributions from microsecond molecular dynamics. Nucleic Acids Res. 2015, 43, 2412–2423.
  48. Fu, H.; Zhang, C.; Qiang, X.-W.; Yang, Y.-J.; Dai, L.; Tan, Z.-J.; Zhang, X.-H. Opposite Effects of High-Valent Cations on the Elasticities of DNA and RNA Duplexes Revealed by Magnetic Tweezers. Phys. Rev. Lett. 2020, 124, 058101.
  49. Cruz-Leon, S.; Vanderlinden, W.; Muller, P.; Forster, T.; Staudt, G.; Lin, Y.Y.; Lipfert, J.; Schwierz, N. Twisting DNA by salt. Nucleic Acids Res. 2022, 50, 5726–5738.
  50. Long, M.P.; Alland, S.; Martin, M.E.; Isborn, C.M. Molecular dynamics simulations of alkaline earth metal ions binding to DNA reveal ion size and hydration effects. Phys. Chem. Chem. Phys. 2020, 22, 5584–5596.
  51. Xi, K.; Wang, F.-H.; Xiong, G.; Zhang, Z.-L.; Tan, Z.-J. Competitive Binding of Mg2+ and Na+ Ions to Nucleic Acids: From Helices to Tertiary Structures. Biophys. J. 2018, 114, 1776–1790.
  52. Krüger, A.; Zimbres, F.M.; Kronenberger, T.; Wrenger, C. Molecular Modeling Applied to Nucleic Acid-Based Molecule Development. Biomolecules 2018, 8, 83.
  53. Oweida, T.J.; Kim, H.S.; Donald, J.M.; Singh, A.; Yingling, Y.G. Faculty Opinions recommendation of Assessment of AMBER Force Fields for Simulations of ssDNA. J. Chem. Theory Comput. 2021, 17, 1208–1217.
  54. Dans, P.D.; Ivani, I.; Hospital, A.; Portella, G.; González, C.; Orozco, M. How accurate are accurate force-fields for B-DNA? Nucleic Acids Res. 2017, 45, 4217–4230.
  55. Cruz-León, S.; Grotz, K.K.; Schwierz, N. Extended magnesium and calcium force field parameters for accurate ion–nucleic acid interactions in biomolecular simulations. J. Chem. Phys. 2021, 154, 171102.
  56. Castelli, M.; Doria, F.; Freccero, M.; Colombo, G.; Moroni, E. Studying the Dynamics of a Complex G-Quadruplex System: Insights into the Comparison of MD and NMR Data. J. Chem. Theory Comput. 2022, 18, 4515–4528.
  57. Havrila, M.; Stadlbauer, P.; Islam, B.; Otyepka, M.; Šponer, J. Effect of Monovalent Ion Parameters on Molecular Dynamics Simula-tions of G-Quadruplexes. J. Chem. Theory Comput. 2017, 13, 3911–3926.
  58. Lazim, R.; Suh, D.; Choi, S. Advances in Molecular Dynamics Simulations and Enhanced Sampling Methods for the Study of Protein Systems. Int. J. Mol. Sci. 2020, 21, 6339.
  59. van Gunsteren, W.F.; Daura, X.; Hansen, N.; Mark, A.E.; Oostenbrink, C.; Riniker, S.; Smith, L.J. Validation of Molecular Simulation: An Overview of Issues. Angew. Chem. Int. Ed. 2018, 57, 884–902.
  60. Betz, R.M.; Dror, R.O. How Effectively Can Adaptive Sampling Methods Capture Spontaneous Ligand Binding? J. Chem. Theory Comput. 2019, 15, 2053–2063.
  61. Markthaler, D.; Fleck, M.; Stankiewicz, B.; Hansen, N. Exploring the Effect of Enhanced Sampling on Protein Stability Prediction. J. Chem. Theory Comput. 2022, 18, 2569–2583.
  62. Kasavajhala, K.; Lam, K.; Simmerling, C. Exploring Protocols to Build Reservoirs to Accelerate Temperature Replica Exchange MD Simulations. J. Chem. Theory Comput. 2020, 16, 7776–7799.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Mathematical & Computational Biology
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Zi-Chun Mu
,
Ya-Lan Tan
,
Jie Liu
,
Ben-Gong Zhang
,
Ya-Zhou Shi
View Times: 271
Revisions: 3 times (View History)
Update Date: 28 Jun 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback