A Taxonomic Survey of Physics-Informed Machine Learning

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Joseph Pateras	--	1240	2023-06-19 19:49:04	\|
2	format correction	Dean Liu	-2 word(s)	1238	2023-06-20 05:10:17	\|

This entry is adapted from the peer-reviewed paper 10.3390/app13126892

Physics-informed machine learning (PIML) refers to the emerging area of extracting physically relevant solutions to complex multiscale modeling problems lacking sufficient quantity and veracity of data with learning models informed by physically relevant prior information.

data-driven machine learning multiphysics modeling physics-informed machine learning

1. Introduction

Building reliable multiphysics models is an essential operation in nearly any given area of scientific research. However, solving and interpreting said models can be an essential limitation for many. As complexity and dimensionality in physical models, so to does the expense associated with traditional methods towards differentiation—such as finite element mesh construction. In addition to numerical hurdles, challenging experimental observation or otherwise unavailable data can also limit the applicability of certain modeling approaches. Furthermore, traditional learning machines fail to learn relationships in many complex physical systems due to the typical imbalance of data for one and the lack of physically relevant knowledge for another. Problems lacking trustworthy observational data are typically modeled by precise systems of complex equations with initial conditions and tuned coefficients.

2. Advancements in Physics-Informed Machine Learning.

Physics-informed machine learning is a tool by which researchers can extract physically relevant solutions to multiscale modeling problems. Crucially, physics-informed learning machines have been shown to accurately learn general solutions to complex physical processes having sparse multifidelity and/or otherwise incomplete data by leveraging the knowledge of the underlying physical features. What differentiates physics-informed learning from traditional statistical model is the somehow tangible inclusion of physically relevant prior knowledge. The constitutional need for qualitatively defined, physically relevant learning interventions further increases the need for a qualitative taxonomy.

Most notable among the recent advancements, researchers focus on the increasing parallelism of the physics-informed neural network algorithm and the introduction of neural operators for learning systems of differential equations. In 2021, Karniadakis et al. ^[1] provided a comprehensive review of the methods leveraged in physics-informed learning and formed an outline of biases catalyzed by prior physical knowledge. Karniadakis et al. assert as a key point, “Physics-informed machine learning integrates seamlessly data and mathematical physics models, even in partially understood, uncertain and high-dimensional contexts” ^[1]. This comprehensive review primarily details physics-informed neural learning machines for applicability to a diverse set of difficult, ill-posed, and inverse problems. Karniadakis et al. continue to discuss domain decomposition for scalability and operator learning as future areas of research. Toward a recent expansion in a wide range of application, the use of physics-informed learning machines has seen the method’s application in diverse fields including fluids ^[2], heat transfer ^[3], COVID-19 spread ^[4]^[5], and cardiac modeling ^[6]^[7]^[8]. Cai et al. ^[2] offer a review of physics-informed machine learning implementations for three-dimensional wake flows, supersonic flows, and biomedical flows. High-dimensional and noisy data from fluid flows are prohibitively difficult to train with traditional learning algorithms; researchers highlights the applicability of physics-informed neural networks tackling this problem in fluid flow modeling. For heat transfer problems, Cai et al. ^[3] discuss a variety of physics-informed machine learning approaches in convection heat transfer problems with unknown boundary conditions, including several forced convection and mixed convection problems. Again, Cai et al. showcase diverse applications of physics-informed neural networks to apply neural learning machines in traditionally impractical settings where injecting physically relevant prior information makes neural network modeling viable. In 2022, Nguyen et al. ^[4] provided an SEIRP-informed neural with architecture and training routine changes defined by governing compartmental infection model equations. Additionally, Cai et al. ^[5] propose the fractional PINN (fPINN), a physics-informed neural network created for the rapidly mutable COVID-19 variants trained on Caputo–Hadamard derivatives in the loss propagation of the training process. Cuomo et al. ^[9] provide a summary of several physics-informed machine learning use cases. The wide range of apt applications for physics-informed machine learning further perpetuates the need for qualitative discussion and subclassification.

The need for computational methods, especially where problems are modeled by complex and/or multiscale systems of nonlinear equations, is growing expeditiously. An exhaustive amount of scholarly thought has recently been afforded toward methods advancing the data-driven learning of partial differential equations. Raissi et al. ^[10] were able to infer lift and drag from velocity measurements and flow visualizations, with Navier–Stokes being estimated using automatic differentiation to obtain the required derivatives and compute the residuals composing loss step augmentations. A similar process is common for learning process augmentations in physics-informed learning. Raissi et al. ^[11] introduced a hidden physics model for learning nonlinear partial differential equations (PDEs) from noisy and limited experimental data by leveraging the underpinning physical laws. This approach uses the Gaussian process to balance model complexity and data fitting. The hidden physics model was applied to the data-driven discovery of PDEs, such as Navier–Stokes, Schrödinger, and Kuramoto–Sivashinsky equations. Later, in another paper, two neural networks were employed for similar problems ^[12]. The first neural network models the prior of the unknown solution, and the second neural network models the nonlinear dynamics of the system. In another work, the same group used deep neural networks combined with a multistep time-stepping scheme to identify nonlinear dynamics from noisy data ^[13]. The effectiveness of this approach was shown for nonlinear and chaotic dynamics, Lorenz system, fluid flow, and Hopf bifurcation. In 2019, Raissi et al. ^[14] also proposed two types of algorithms: continuous-time and discrete-time models. The so-titled physics-informed neural network is tailored to two classes of problems as follows: (a) the data-driven solution of PDEs and (b) the data-driven discovery of PDEs. The approach’s effectiveness was demonstrated for several problems, including Navier–Stokes, Burgers’ equation, and Schrödinger equations. Consequently, the PINN has been adapted to intuit governing equations or solution spaces for many types of physical systems. For Reynolds-averaged Navier–Stokes problems, Wang et al. ^[15] propose a physics-informed random forest model for assisting data-driven flow modeling. Other research introduce physics constraints, consequently biasing the learning process driven by prior relevant knowledge. Sirignano et al. ^[16] accurately solved highly-dimensional free-boundary partial differential equations and proved the approximation utility of neural networks for quasilinear partial differential equations. Han et al. ^[17] proposed a deep learning method for high-dimensional partial differential equations with backward stochastic differential equation reformulations. Rudy et al. ^[18] propose a method for estimating governing equations of numerically derived flow data using automatic model selection. Long et al. ^[19] proposed another data-driven approach for governing equation discovery, and Leake et al. ^[20] introduce the combination of the deep theory of functional connections with neural networks to estimate solutions to partial differential equations. The preceding selection includes examples of the transition from solving partial differential equations with expensive techniques for learning solutions with high-throughput learning machines, and researchers cover some works on the latter topic next. Figure 1 show how physics-informed machine learning is used in the learning process to accelerate training and allow applicability of models to problems whose data inconsistencies have posed obstacles to traditional learning.

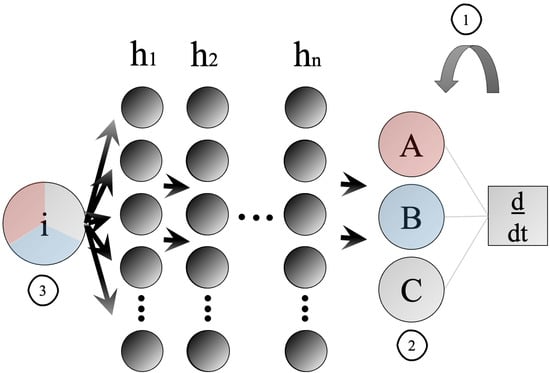
Figure 1. The popular PINN architecture aptly exemplifies the three biases informing learning processes: (1) learning bias, (2) inductive bias, and (3) observational bias.

In neural networks, as Figure 1 shows, (1) learning bias in the form of physically relevant modeling equations is used directly in training error propagation, (2) inductive bias through neural model architecture augmentation, is used to introduce previously understood physical structures, and (3) observational bias in the form of data-gathering techniques is used to introduce physical bias via informed data structures of simulation or observation. Here, i are input features.

h_{i}

display an arbitrary number of hidden layers of arbitrary size. A, B, and C are physically relevant structures. For example, in compartmental epidemiology, the population bins and their underlying governing equations are differentiated in process (1).

References

Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440.
Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738.
Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks for Heat Transfer Problems. J. Heat Transf. 2021, 143, 060801.
Nguyen, L.; Raissi, M.; Seshaiyer, P. Modeling, Analysis and Physics Informed Neural Network approaches for studying the dynamics of COVID-19 involving human-human and human-pathogen interaction. Comput. Math. Biophys. 2022, 10, 1–17.
Cai, M.; Karniadakis, G.E.; Li, C. Fractional SEIR model and data-driven predictions of COVID-19 dynamics of Omicron variant. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 071101.
Costabal, F.S.; Yang, Y.; Perdikaris, P.; Hurtado, D.E.; Kuhl, E. Physics-Informed Neural Networks for Cardiac Activation Mapping. Front. Phys. 2020, 8, 42.
Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2019, 358, 112623.
Grandits, T.; Pezzuto, S.; Costabal, F.S.; Perdikaris, P.; Pock, T.; Plank, G.; Krause, R. Learning Atrial Fiber Orientations and Conductivity Tensors from Intracardiac Maps Using Physics-Informed Neural Networks. Funct. Imaging Model. Heart 2021, 650–658.
Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88.
Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2018, 861, 119–137.
Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141.
Raissi, M. Deep Hidden physics-Models: Deep Learning of Nonlinear Partial Differential Equations. J. Mach. Learn. Res. 2018, 19, 1–24. Available online: https://www.jmlr.org/papers/volume19/18-046/18-046.pdf?ref=https://githubhelp.com (accessed on 9 January 2023).
Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Multistep Neural Networks for Data-driven Discovery of Nonlinear Dynamical Systems. arXiv 2018, arXiv:1801.01236.
Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2018, 378, 686–707.
Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603.
Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364.
Han, J.; Jentzen, A.; E, W. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510.
Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614.
Long, Z.; Lu, Y.; Ma, X.; Dong, B. PDE-Net: Learning PDEs from Data. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Available online: http://proceedings.mlr.press/v80/long18a.html?ref=https://githubhelp.com (accessed on 4 May 2023).
Leake, C.; Mortari, D. Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations. Mach. Learn. Knowl. Extr. 2020, 2, 37–55.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence; Mathematical & Computational Biology

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Joseph Pateras

Pratip Rana

Preetam Ghosh

View Times: 250

Update Date: 20 Jun 2023

Table of Contents

Video Upload Options

Confirm

1. Introduction

2. Advancements in Physics-Informed Machine Learning.

References