Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Sashini Pathirana
 -- 5597 2023-06-07 12:03:21 |
2 layout
Sirius Huang
 Meta information modification 5597 2023-06-08 03:01:20 | |
3 layout
Sirius Huang
 Meta information modification 5597 2023-06-09 10:28:11 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Pathirana, S.; Lambot, S.; Krishnapillai, M.; Cheema, M.; Smeaton, C.; Galagedara, L. Ground-Penetrating Radar in Soil Studies. Encyclopedia. Available online: https://encyclopedia.pub/entry/45285 (accessed on 26 December 2024).
Pathirana S, Lambot S, Krishnapillai M, Cheema M, Smeaton C, Galagedara L. Ground-Penetrating Radar in Soil Studies. Encyclopedia. Available at: https://encyclopedia.pub/entry/45285. Accessed December 26, 2024.
Pathirana, Sashini, Sébastien Lambot, Manokarajah Krishnapillai, Mumtaz Cheema, Christina Smeaton, Lakshman Galagedara. "Ground-Penetrating Radar in Soil Studies" Encyclopedia, https://encyclopedia.pub/entry/45285 (accessed December 26, 2024).
Pathirana, S., Lambot, S., Krishnapillai, M., Cheema, M., Smeaton, C., & Galagedara, L. (2023, June 07). Ground-Penetrating Radar in Soil Studies. In Encyclopedia. https://encyclopedia.pub/entry/45285
Pathirana, Sashini, et al. "Ground-Penetrating Radar in Soil Studies." Encyclopedia. Web. 07 June, 2023.
Ground-Penetrating Radar in Soil Studies
Edit
This entry is adapted from the peer-reviewed paper 10.3390/rs15112932

Information on the spatiotemporal variability of soil properties and states within the agricultural landscape is vital to identify management zones supporting precision agriculture (PA). Ground-penetrating radar (GPR) and electromagnetic induction (EMI) techniques have been applied to assess soil properties, states, processes, and their spatiotemporal variability. 

ground-penetrating radar hydro-geophysics precision agriculture soil studies

1. Introduction

Precision agriculture (PA), supported by various technologies, is a rapidly emerging field for managing the agricultural landscape on a large scale by considering the field variability for increasing agricultural productivity while minimizing negative environmental impacts and the production cost [1][2][3]. Agricultural practices such as irrigation, land preparation, and fertilization are typically applied uniformly across the entire field, treating the heterogeneous fields as homogeneous. However, the spatial and temporal heterogeneity of the agricultural landscape can be effectively monitored through implementing different technologies to support PA, including (1) geographic information systems (GIS), (2) satellite-based global positioning systems (GPS), (3) remote sensing, (4) drones, (5) the Internet of Things, (6) artificial intelligence, and (7) different proximal sensors, for example, geophysical techniques [1][4][5]. These digital technologies are applied to collect, process, monitor, and map the spatiotemporal variability of the agricultural landscape. Their purpose is to improve agronomic performance, enhance crop productivity and develop decision support tools [1][3][6][7][8][9][10][11][12][13]. By utilizing the latest technologies, such as unmanned aerial vehicles, agricultural machinery, and robotic technologies, the required amounts of water, nutrients, and agrochemicals for plant growth and development can be accurately applied to specific locations within the agricultural landscape and within the appropriate timeframe [1][4][6][8][9][14][15][16]. PA offers several benefits, including improved soil fertility and health, increased water productivity and food security, minimized soil and water pollution, and reduced labor force requirements, as well as the overuse of resources such as water, fertilizer, seeds, and energy, leading to lower production costs [4][6][14][17][18]. The incorporation of spatiotemporal variability mapping with geo-statistics and GIS marked a major advance in PA to a new level to identify management zones [7][8][19].
The spatiotemporal variability of crop factors and subsurface physical, chemical, and hydrological properties, and processes are crucial in PA [1]. Hydro-geophysics is an efficient approach that includes multi-scale probing and high-resolution imaging techniques for accurately obtaining the spatiotemporal variability of the subsurface hydrological processes and soil properties [20][21][22][23]. Traditional methods such as soil sampling and laboratory analysis are destructive, labor-intensive, costly in large scales, time-consuming, and mainly provide point scale measurements only [1][20][24][25]. Commonly used geophysical techniques in hydro-geophysics are electrical resistivity tomography, electromagnetic induction (EMI), self-potential, ground-penetrating radar (GPR), induced polarization, surface nuclear magnetic resonance, gravity, magnetics, and seismic methods [23][24][25][26]. 

2. Basic Operating Principles of Ground-Penetrating Radar

GPR is a near-surface electromagnetic proximal sensor commonly used in agriculture and environmental applications [27][28][29]. Commercially available GPR systems use unguided electromagnetic waves with frequencies ranging from 10 MHz to 3600 MHz [28][30]. Resolution and depth of penetration are vital factors of GPR applications. Radar wave propagation velocity and wave attenuation depend on primary electromagnetic properties such as the relative dielectric permittivity (εr), electric conductivity σ, and magnetic permeability (µ) of the soil/media [28][29]. εr is mainly controlled by the water content of the subsurface as the permittivity of liquid water overwhelms those of other soil constituents [28][31]. Equation (1)
v = c ε r
shows the relationship between velocity (v) and εr, where c is the propagation velocity of electromagnetic waves in free space, which is equal to the speed of light (0.3 m/ns) [28]. The penetration depth of GPR is mainly determined by the σ of subsurface materials and the operation frequency [27][28][32][33]. When EM waves travel through conductive materials, EM energy is lost as heat through the electrical current. In addition, energy loss in EM waves is due to increasing operating frequency and scattering. This energy loss is called attenuation and, therefore, reduces the penetration depth of GPR waves [27][28][34][35]. GPR wave attenuation also results from geometrical spreading in 3D wave propagation. The resolution of GPR increases with increasing frequency, increasing bandwidth, and decreasing wave velocity, since the wavelength (λ) is inversely proportional to the frequency (f) and directly proportional to the velocity (λ = v/f) [35][36][37]. The radiation pattern of a GPR antenna is the primary determinant of its footprint, which is the subsurface area illuminated by the radiation emitted from the antenna. The shape and extent of the radiation pattern depend on several factors, including the antenna design, frequency, size, shape, and dielectric properties of the subsurface. The beam width of the radiation pattern is also affected by the dielectric permittivity of the subsurface, with higher permittivity resulting in a narrower beam.
The most common GPR system consists of an impulse generator that repeatedly sends a source of a particular voltage and frequency to a transmitting antenna. It is worth noting that frequency-domain radars are also available in addition to impulse radars and are also referred to as time-domain radars [38]. They operate by successively transmitting continuous waves over a specific frequency range. Ground-coupled and air-coupled horn antennas are used for on-ground and air-borne GPR surveys, respectively (Figure 1).
Remotesensing 15 02932 g002 550
Figure 1. Ground-penetrating radar (GPR) surveys with (a) ground-coupled antennas (GPR instrument by S. Pathirana), (b) air-coupled antennas (GPR prototype by S. Lambot).
A commonly used GPR system consists of two antennas: a transmitter (Tx) and a receiver (Rx) or multiple receivers. The TX generates electromagnetic waves, following the frequency-dependent antenna radiation pattern, which travels through the air, air-surface interface, and subsurface. As shown in Figure 2, the Rx receives airwave, direct ground wave (DGW), reflected wave, and refracted waves [27][28][39]. EM wave reflection or refraction at a boundary depends on different electrical properties (mainly εr in most GPR applications) of the layer above and below the boundary [40].
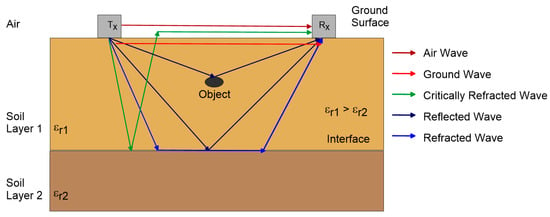
Remotesensing 15 02932 g003 550
Figure 2. Ray paths of ground-penetrating radar (GPR) wave propagation in a two-layer soil which has different dielectric permittivity values (modified from Huisman et al. [32]).
GPR applications have three main data acquisition modes: (1) reflection profiling, (2) velocity-sounding, and (3) transillumination [27][28][35]. In the reflection profiling method, the Tx and Rx antennas are kept in a fixed antenna separation, orientation, and station interval, and both antennas are moved along the survey direction [27]. This method is called the common offset method or fixed offset method (FOM) and produces a vertical 2D image of the subsurface reflections (Figure 3a) [35][41]. The GPR velocity-sounding method can be performed using the common mid-point (CMP) method or the wide-angle reflection and refraction (WARR) method. In the CMP method, Tx and Rx are moved apart from each other by keeping the midpoint between the two antennas fixed (Figure 3b). However, in the WARR method, one antenna (Tx, for example) is kept at a fixed location, and the other antenna (Rx) is moved away by increasing the antenna offset (Figure 3c). The objectives of the velocity-sounding methods are to estimate the velocity by measuring the two-way travel times for different antenna offsets and then finding the slope of the relationship between the squared travel time and antenna offset [27][35]. The transillumination survey method places the Tx and Rx on opposite sides of the medium. Under transillumination, zero-offset profiling (ZOP) is a quick method to find anomalous zones by moving Tx and Rx from one station to another at a predetermined step size (Figure 3d). In the multi-offset gathering (MOG) mode, one antenna (Tx) is kept stationary while the other antenna (Rx) is moved to multiple locations to produce tomographic imaging (Figure 3e). In vertical reflection profiling (VRP), Tx is placed on the surface, and Rx is placed in the borehole since this method has many advantages over ZOP and MOG (Figure 3f). The data acquisition method and frequency selected in each survey are based on the application requirements and field conditions [27][28][42][43].
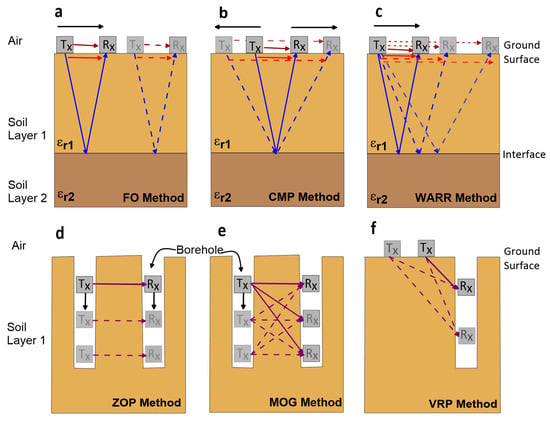
Remotesensing 15 02932 g004 550
Figure 3. Data acquisition methods in ground penetration radar (GPR) applications, (a) fixed offset, (b) common mid-point, (c) wide-angle reflection and refraction, (d) zero offset profiling, (e) multiple offsets gathering, and (f) vertical reflection profiling methods (modified from Liu et al. [44]).

3. Applications of Ground-Penetrating Radar in Soil Studies

This section discusses the applications of GPR to estimate soil properties; states such as SWC, porosity, compaction, salinity, texture, SOM, and other applications such as depth to the groundwater table and capillarity.

3.1. Soil Water Content

SWC estimation is the most extensively used and well-developed GPR application in soil studies. The large-scale estimation and mapping of the spatiotemporal variability of SWC are critical across the agricultural landscape, but these are difficult tasks to complete with traditional methods. For example, mapping high resolution SWC variability using GPR provides the information necessary to optimize the amount of water required for and the timing of crop irrigation. According to previous studies, volumetric soil water content (SWCV) can be estimated from GPR using various methods such as the reflected wave velocity method, DGW velocity method, transmitted wave velocity method (in boreholes), surface reflection coefficient method, average envelope amplitude (AEA) method, and full-waveform inversion (FWI) method. Subsurface SWC influences the propagation velocity of GPR waves since εr varies with SWC and velocity varies with εr [35][45]. The well-established and widely used Topp’s equation [31] estimates SWCV from εr. Capacitance probes, neutron probes, the gravimetric method, and time domain reflectometry (TDR) are used for validating GPR-estimated SWC [41][43][46][47][48][49][50][51][52].
  • Reflected wave velocity method
The reflected wave velocity method is used to acquire SWCV in deeper soil layers. However, reflectors such as isolated objects or interfaces are required to obtain the travel time of the reflected radar wave. Natural reflectors such as rocks and roots and artificial reflectors such as pipes are point reflectors, while lithologic layers and the water table are interfaces [33][47][48][53][54][55]. The two-way travel time of the GPR wave above the reflector is measured and converted into radar wave velocity, then to εr, and is then used to calculate the SWCV [52][56][57]. The velocity of the reflected wave is obtained using an FOM or multiple offset methods (MOM): CMP or WARR. When the depth of the reflector is known, the reflected wave velocity is estimated in the FOM by dividing the depth of the reflector by the two-way travel time. Lunt et al. [56] applied the reflected wave velocity method under natural conditions, while Stoffregen et al. [58], Loeffler and Bano [59], Ercoli et al. [57], and Zhou et al. [60] applied it under controlled conditions to obtain SWCV. With advanced analysis techniques, the average velocity of a reflector can be obtained by fitting a hyperbola [52][61][62][63]. On the other hand, CMP and WARR methods are applied as multiple offset methods when the depth of the reflector is unknown. However, data collection and processing in this method are time-consuming and labor-intensive [30][44]. Steelman and Endress [64] applied the multi-frequency CMP method in three different sites to estimate the vertical variation of SWCV with the reflected wave method during a complete annual cycle, including wetting/drying and freezing/thawing. The reflection method for determining SWCV has some limitations, as it depends on the continuous availability of reflectors, especially in shallow soils [52].
b.
Direct ground wave velocity method
On the other hand, the DGW velocity method of GPR can be used to estimate the SWCV of shallow (uppermost centimeters) soils without employing a reflector [41][44][47][50][65]. Both the FOM and MOM can be used to estimate SWCV from the direct ground wave, though the MOM is time-consuming and laborious compared to the FOM [41][65]. To address this, Sperl [37] established a method to estimate SWCV over a large area by combining the MOM and FOM. In this method, the MOM only decides the most suitable antenna separation to distinguish between the DGW and the direct airwave. Then, the FOM is applied with the decided antenna separation to collect data effectively over a large area [44][66]. Huisman et al. [65] assessed the accuracy of DGW to estimate and map SWCV over a large area with WARR and the FOM (single trace analysis). The accuracy of SWC estimated based on WARR measurements was ±0.030 m3/m3, while it was ±0.037 m3/m3 based on the FOM when compared with the TDR method. Therefore, the authors suggested that the available TDR calibrations, such as Topp’s equation [31], can also be applied to GPR [65]. Furthermore, the authors suggested that the most appropriate assessment between electromagnetic methods (TDR and GPR) is εr, rather than SWCV. Galagedara et al. [41] and Huisman and Bouten [49] discussed the importance of accurate time-zero calibration to estimate SWCV using the DGW method. Huisman and Bouten [49] conducted a sensitivity analysis to study time-zero error at zero antennae offset with WARR measurements. The authors found that GPR simulations could not account for the meantime shift at zero offset due to the time-picking error and SWCV heterogeneity in the sensitivity analysis. Galagedara et al. [41] suggested an accurate and stable time-zero picking methodology to estimate SWCV with an error rate of less than 1% under variable water contents.
Huisman et al. [67] found that GPR is an efficient technique to map SWCV over an agricultural landscape, and GPR-estimated water content matched well with TDR results. The accuracy and spatial and temporal variability of the SWC under different water contents, such as irrigation and drainage conditions, have been studied by several researchers [41][48][50][53][67][68][69][70]. In addition, SWC variation under dry and rainy seasons was studied by Thitimakorn et al. [71], while Cao et al. [72] studied three-dimensional soil water dynamics before and after heavy rainfall. These studies compared SWC estimated from the DGW and found good agreements with TDR or gravimetric methods as standard methods. Weihermüller et al. [73] mapped the spatial variability of SWC with the DGW method at a silty loam site with 450 MHz center frequency antennas. However, Weihermüller et al. [73] compared GPR (450 MHz)-estimated SWCV with TDR and volumetric samples and found that the results of the GPR did not agree well with that of the TDR and volumetric samples. The reason behind this was reported to be the high signal attenuation of the GPR due to the relatively high clay content present [73].
However, previous studies have also identified some issues with the DGW method. It is challenging to distinguish the direct airwave and DGW under dry conditions since the velocity of GPR is high. Therefore, the DGW also reaches the Rx rapidly and interferes with the direct airwave [41][53][70]. The effective penetration depth of the GPR DGW varies with the soil texture, antenna frequency, and wet/dry conditions present [41][46][50][66][74]. The heterogeneity of the upper soil layer can produce reflections which interfere with DGW. Radar wave attenuates with higher conductivity, and therefore, the penetration depth decreases with increases in high-conductive materials such as clay. Galagedara et al. [75] applied a numerical model to investigate the effective sampling depth of the GPR DGW in terms of antenna frequency and dry/wet two-layer conditions. The authors found that the penetration depth of the DGW decreases with increasing frequency and wetness since the sampling depth is a function of the wavelength [37][66][75]. Table 2 summarizes the previous studies related to the penetration depth of the GPR DGW when estimating SWC.
Table 2. Summary of the effective depth of the ground-penetrating radar direct ground wave studies.
Frequency
(MHz)		 Soil Type Effective Depth (m) Source
200 Silty clay 0–0.10 (wet condition) Chanzy et al. [46]
200 Aeolian sand (Podzolic) 0–1.20 van Overmeeren et al. [47]
50 Aeolian sand (Podzolic) 0–3.00 van Overmeeren et al. [47]
900 Clay to loamy sand 0–0.20 Hubbard et al. [48]
450 Sandy loam 0–0.20 (wet condition) Galagedara et al. [41]
450 Sandy loam and
sandy clay loam		 0–0.11 (wet condition)
0–0.14 (dry condition)		 Grote et al. [53]
900 Sandy loam and
sandy clay loam		 0–0.07 (wet condition)
0–0.10 (dry condition)		 Grote et al. [53]
100 Sandy loam 0–0.85 (A)
0–0.50 (B)		 * Galagedara et al. [75]
200 Sandy loam 0–0.38 (A)
0–0.26 (B)		 * Galagedara et al. [75]
450 Sandy loam 0–0.26 (A)
0–0.16 (B)		 * Galagedara et al. [75]
900 Sandy loam 0–0.13 (A)
0–0.09 (B)		 * Galagedara et al. [75]
250 Sand 0–0.15 Pallavi et al. [76]
400 Loamy soil 0.10–0.20 (wet condition)
0.10–0.30 (dry condition)		 Thitimakoran et al. [71]
* Modelling results: A—dry over wet layer; B—wet over dry layer.
c.
Transmitted wave velocity method
In the transmitted wave velocity method, both the Tx and Rx antennas are placed in boreholes or in surface drains, and the direct wave passing through the media is used to estimate the SWCV [42][43][77][78][79][80]. In the early stage, ZOP and MOG measurements were widely applied. However, using ZOP and MOG, direct waves interfere with reflected and critically refracted waves in low-velocity zones and underestimate the SWC. Therefore, VRP was introduced [81][82][83]. VRP requires only one borehole; thus, the ground disturbance and cost are relatively low. Across several studies, the transmitted wave velocity method was applied to estimate SWCV [42][77][79][80], even though the method is not widely used to estimate SWCV at the root zone in agriculture [42][78][80]. Nevertheless, Wijewardana and Galagedara [43] applied the transmitted direct wave method to estimate SWCV in raised bed agricultural fields, where Tx and Rx were moved along the surface drains of raised beds.
d.
Surface reflection coefficient method
The surface reflection coefficient method is an off-ground GPR technique; both antennas are moved above ground, and the SWCV is estimated based on the amplitude of the reflected wave at the soil surface. The underlying equations and modeling hypotheses are detailed and discussed in particular detail in Lambot et al. [84]. This method determines the reflection coefficient (R) using the amplitude of the reflections from the soil surface (A). The amplitude of the reflections from the perfect electric conductor (APEC) is positioned at the same distance as the soil (Equations (2) and (3)). Adekani. [70], al Hagrey and Müller [85], Redman et al. [86], and Redman et al. [87] applied this method to estimate SWC. This method is more suitable for agricultural applications such as optimizing seeding depth and irrigation management in very thin upper soil layers [0–0.10 m] [70]. However, the practical applicability of the GPR surface reflection coefficient method for estimating soil moisture is constrained by its sensitivity to calibration height, which is difficult to maintain consistently in real-world field applications. Moreover, the method relies on a simplified assumption of 1D propagation, which does not account for the antenna, further limiting its accuracy.
R = 1   − ε r ( soil ) 1 + ε r ( soil )
R = A A PEC
e.
Average envelope amplitude method
When estimating the SWC using the DGW with the FOM, differentiating the DGW and the direct air wave is often challenging. To avoid this problem, Pettinelli et al. [88] proposed a method to analyze early time signal amplitude (first arrival direct wave—a combined direct airwave and DGW) without considering the separate travel times of the direct air and ground waves. In the AEA method, SWC is assessed by correlating εr variation with attributes of the early time signal of GPR [88][89]. Furthermore, the AEA is sensitive to both εr and σa and changes in waveform attributes such as shape, amplitude, and duration with changing εr and σa [88][90]. Pettinelli et al. [88] applied the AEA of the early time signal to estimate the SWC in a controlled field condition, Ferrara et al. [91] applied it under natural field conditions, and Ferrara et al. [92] applied it under laboratory conditions. Algeo et al. [93] compared two early time signal analysis methods—the AEA method and the carrier frequency amplitude method—to map SWC and found that both methods have strengths and weaknesses. Another study assessed the applicability of AEA in early time signals to study SWC during irrigation and showed the possibility of this method in estimating SWC in clay-rich soils [90]. However, this AEA method is still in development, and further research studies are needed to estimate soil properties under different field conditions.
f.
Full waveform inversion method
FWI is a numerical modeling method that retrieves the unknown εr and/or σ distribution from a known EM field by fitting a full-wave EM model to the radar measurements [38]. The EM model tries to describe the radar signal, including the radar source, antenna(s), antenna(s)—medium interactions, and the medium, as accurately as possible. Ernst et al. [94], Klotzsche et al. [95], Meles et al. [96], Klotzsche et al. [97], Gueting et al. [98], and Yu et al. [99] applied FWI for borehole GPR experiments. Lambot et al. [38][100][101], Jonard et al. [102][103], Minet et al. [69], and de Mahieu et al. [104] applied FWI for air-coupled GPR configurations to estimate SWC. The method was recently used with a drone-borne GPR (Figure 4) for high-resolution soil moisture mapping in agricultural fields [105]. The radar equation used in these studies was also generalized to near-field or on-ground GPR conditions [101][106][107], thereby opening new avenues for agricultural applications. FWI has proven to be a powerful tool for extracting the maximum information from GPR data and facilitating automated data processing. However, the application of FWI has been limited by the inherent complexity of the underlying electromagnetic model and the associated data processing requirements. In that respect, within the framework of the EU’s agROBOfood project, called MIRAGE (grant agreement Nº 825395, 2021–2023), a specifically dedicated radar and software for soil moisture mapping, namely, gprSense, has been developed (https://www.gprsense.com, accessed on 26 December 2022, Sensar Consulting, Belgium) [108]. gprSense implements the full-wave radar equation introduced by Lambot et al. [109] in a user-friendly software platform with an intuitive interface. This tool enables real-time automated FMI and the streaming of soil moisture data, making it accessible to both basic users and advanced scientists.
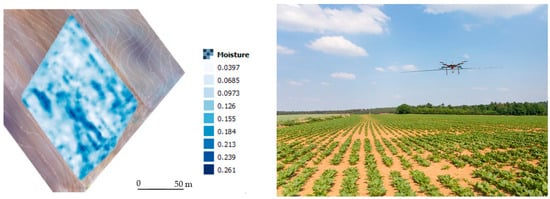
Remotesensing 15 02932 g005 550
Figure 4. High-resolution soil moisture map obtained with drone-borne GPR and full-wave inversion (FWI) in an agricultural field in Belgium (GPR prototype by S. Lambot).
Traditionally, the reflection coefficient at the soil surface is assumed to depend solely on the contrast in dielectric permittivity (εr) between the soil and the air. However, for frequencies below 100 MHz, the soil conductivity (σ) can also significantly influence the reflection coefficient [84]. At these low frequencies, the sensitivity of the reflection to σ becomes higher than that of εr. Wu and Lambot [105] proposed a new method for mapping soil σ using relatively low-frequency drone-borne GPR and full-wave inversion techniques. Their method works best when the dielectric permittivity and conductivity are not too large. Although the sensitivity to εr is not negligible in this frequency range, their method demonstrated good agreement with the σ values obtained from EMI surveys.

3.2. Soil Porosity and Soil Compaction

Soil porosity indirectly influences GPR propagation wave velocity and amplitude. When pore spaces are filled with water, it changes the εr, which changes the v. Therefore, εr at saturation can be used as an indicator of total porosity [110][111][112][113][114]. Macro-pores can trap more water during saturation (irrigation and excess rainfall) since their infiltration rate is high, but water will drain quickly due to gravity and become dry [115]. This phenomenon will affect the velocity of GPR waves, where velocity decreases during infiltration and increases during drainage. This velocity variation is rapid in coarse-textured soils, and wetting and drying are faster than in fine-textured soils. Micropores can hold more water against gravity through capillary action, and micropores are more common in clay soil, even though the GPR waves attenuate due to the high σ of clay [112][115].
Different researchers initially assessed soil porosity using GPR wave velocity [110][111][113][116]. However, a reliable method to estimate porosity, bulk density, soil compaction, or soil penetration resistance using GPR has yet to be developed and tested. In unsaturated soils, pore spaces are filled with both water and air. The relationship between soil porosity, soil water saturation, and SWCv is crucial when finding the porosity with GPR. If the soil water saturation is known, porosity can be estimated since SWCv can be obtained from GPR [114]. Additionally, under fully saturated conditions, SWCV is equal to the soil porosity [115][116]; thus, GPR can be used to estimate soil porosity by measuring the SWCV at saturation.
Due to the difficulty of estimating porosity alone with GPR, researchers have integrated other geophysical techniques and different theoretical and empirical approaches with GPR. Laboratory-scale experiments were conducted to estimate soil porosity using GPR [111][113][117] and field-scale experiments [110][114]. However, the differences between the experimental scales and laboratory-scale measurements must be tested before their application to field conditions [113][117].
Turesson [110] estimated the porosity and soil water saturation of sand, and Khalil et al. [114] estimated the porosity and soil water saturation of a sandstone aquifer using GPR and resistivity techniques using both Topp’s equation (Equation (1) and Archie’s equation (Equation (2)). Ghose and Slob [113] assessed the porosity and soil water saturation of shallow subsoil by developing integrated GPR-seismic techniques through numerical modeling. Meanwhile, Lai et al. [111] proposed a new method to determine porosity using GPR, namely, the cyclic moisture variation technique. In this method, the authors determined the variation of εr and soil water saturation from a partially saturated state to a fully saturated state of the soil and modified the CRIM equation (Equation (3)) to obtain the porosity.
Researchers have also applied GPR to assess the effect of heavy machinery on soil compaction, a serious problem in agricultural fields [118][119][120]. With compaction, porosity decreases, consequently increasing the bulk density and penetration resistance, thereby reducing water infiltration [118][121]. Previous studies showed that compaction changes GPR attributes, i.e., propagation wave velocity and amplitude [118][119][120][121][122][123]. Moreover, researchers found a negative correlation between GPR wave amplitude and compaction/penetration resistance [118][119][120][121]. This negative correlation may be due to reduced free water and increased bound water in the soil structure, resulting in increased water-soluble salts in soil pore water, thereby increasing the soil’s bulk σ and attenuating GPR waves and decaying the wave amplitudes [121]. Another reason could be that increasing the soil density increases the EM wave reflection more than the transmission; hence, the EM energy, wave amplitude, and penetration depth decrease [121]. On the other hand, Akinsunmade et al. [118] and Akinsunmade [119] found that GPR signals penetrate deeper depths in compacted areas than in uncompacted areas. With soil compaction, porosity, and SWC, εr decreases, while GPR wave velocity and wavelength increase, increasing the penetration depth [118][119][120].

3.3. Soil Salinity

Soil σ is the best parameter to use to estimate soil salinity [27][124][125]. In agricultural fields, soil σ is temporally unstable since it frequently changes, mainly with SWC, due to, for example, irrigation, drainage, leaching, evapotranspiration, fertilizer application, and other soil amendments [125][126]. Soil σ is mainly measured using: (1) saturated paste extract electrical conductivity (σe); (2) apparent electrical conductivity (σa); and (3) soil water electrical conductivity (σw). The estimation of the σe of the soil using soil samples in the laboratory is the standard method [34][127] for soil salinity measurements. This standard method is time-consuming, laborious, and costly for large-scale applications. Therefore, electrical resistivity, EMI, and TDR techniques are widely used as alternative methods. However, these alternative methods provide the σa of the subsurface but not the σw or σe [125][128][129][130][131][132][133]. The three main current flow pathways contributing to the σ are the liquid, solid–liquid, and solid phases [129][134]. However, σw is the most appropriate measurement since it is the salinity experienced by plant roots. σw is impossible to obtain directly using alternative methods in the field, and it is difficult to measure in the laboratory [128][129]. In the literature, soil salinity is expressed in different ways using terms such as σa, σw, σe, and σ at different soil: water (σ 1:1, σ1:2, and σ1:5) ratios. The σ of the solid phase (σs) is an important property in agricultural soils and a key variable in PA. It strongly correlates to clay content, a textural property that strongly influences soil water storage, dynamics, and plant growth. Together with SWC, σs significantly impacts the measured σa, making it an excellent surrogate for mapping clay content, usually with EMI [128][129].
Researchers have identified that the influence of σ on GPR wave propagation limits GPR applications, including in agricultural soils. In most applications, such as locating buried objects or utilities and stratigraphic studies, a high σ restricts the GPR signal penetration due to attenuation [28][34][36][45]. Soils with high clay content (illite and montmorillonite) have a high CEC and high σ, leading to higher GPR signal attenuation in clay-rich soils [27][35][36]. However, this limitation (i.e., the influence of σ on GPR wave propagation) can be used as an opportunity in other applications, such as contamination mapping, identifying highly saline areas in PA, and seawater intrusion.
Mimrose et al. [135] studied the influence of irrigation water salinity on the GPR signals using different salt-water concentrations. The authors showed that the amplitude of the GPR reflected wave is inversely proportional to irrigation water salinity. Ferrara et al. [92] applied the early time GPR amplitude analysis method to find the influence of the σ on GPR wave amplitude under uniform εr conditions using salt-water. In this study, the authors found a high correlation between σ and GPR reflected wave amplitude. Alsharahi et al. [136] used a numerical modeling approach to estimate reflections from iron bars and plastic bottles to evaluate the effect of εr and σ on GPR waves and found that the reflected wave amplitude decreases as σ increases. Wu et al. [133] assessed σ variations by applying the waveform comparison method under different conductivities by implementing the GPR reflection coefficient method.
In previous studies, GPR was applied to identify and map soil contaminants such as excess fertilizers, soil amendments, leachates from dump sites, and hydrocarbons. Wijewardana et al. [137][138][139] studied the effect of inorganic contaminants produced from landfill leachate on the GPR responses through field studies, controlled lysimeters, and a modeling approach. The authors found that GPR signal strength decreases with increasing contaminant concentrations due to increasing σ in contaminant plumes. The reflected wave disappeared completely at high σ levels due to attenuation [139]. Reflected wave amplitude decreased with increasing σ, and further research in this field was suggested, since these methods could potentially evaluate σ variation in the subsurface and contamination mapping using the reflected wave amplitude [135][139][140]. The R at an interface increases as the σ contrast increases. Nevertheless, as σ attenuates GPR waves in a given layer, it lowers the amplitude of the reflection amplitude for the lower interfaces. Under laboratory conditions, full-wave inversion was successfully used to retrieve soil conductivity (σ), as demonstrated by Lambot et al. [38]. However, in field conditions with unknown subsurface layering, the inverse problem becomes ill-posed, and the retrieval of σ becomes challenging.

3.4. Soil Hydraulic Properties

As described by the water retention curve and hydraulic conductivity function, unsaturated soil hydraulic properties govern subsurface water dynamics [115]. Hence, as GPR permits the characterization of SWC, time-lapse GPR offers the possibility to characterize these properties through the monitoring of SWC and its dynamics [141][142]. This requires the coupling of the GPR derived-soil moisture or a GPR data processing algorithm with a soil hydrodynamic model, for example, one based on Richards’ equation [143]. For instance, Binley et al. [77], Rucker and Ferré [82], Cassiani and Binley [144], and Kowalsky et al. [145] applied borehole GPR and tomographic inversion to monitor the distribution of water between boreholes and infer soil hydraulic properties. Lambot et al. [38] remotely characterized the hydraulic properties of a laboratory soil column using full-wave GPR data inversion and subsequent soil hydrodynamic inversion. Lambot et al. [84] introduced an integrated 3D full-wave electromagnetic and 1-D hydrodynamic inverse modeling procedure to estimate the soil hydraulic properties from far-field GPR measurements. The method was further studied and applied in the field by Jadoon et al. [146][147]. Tran et al. [106] used data assimilation techniques based on a maximum likelihood ensemble filter to estimate the soil hydraulic properties and reconstruct continuous soil moisture profiles. Despite the promising perspectives for environmental engineering applications shown in these studies, the utilization of joint GPR and hydrodynamic modeling approaches has proven to be challenging, particularly in the agricultural context, because the parameterization of these models is complex and requires a detailed understanding of the soil stratigraphy, petrophysical relationships, and boundary conditions for the hydrodynamic model.

3.5. Groundwater Table and Capillary Fringe Reflection

Determining the depth to the groundwater table (DGWT) is crucial in water management because DGWT affects groundwater recharge, water supply to plants, and contaminant accumulation and transport (especially agrochemicals) [148][149]. Capillary fringe and the groundwater table fluctuate with seasonal variations, affecting agricultural water management, especially during the growing season. Indirect geophysical techniques such as GPR and seismic and resistivity techniques have been employed as alternative methods to traditional destructive piezometer installation when estimating DGWT. GPR is appropriate to estimate the DGWT of shallow aquifers (0–30 m) non-destructively on a large-scale [145][150][151][152][153]. Information on the groundwater table fluctuation during the growing season is vital to understand the water availability for crops through capillarity and groundwater contamination potentials due to agricultural inputs.
The soil above (i.e., unsaturated) and the soil below (i.e., saturated) the water table have different SWCs and thus have different εr values [31][148][151][154][155][156]. Therefore, due to the contrast in εr at the interface, the water table can be identified in the radargrams [151][154][157]. Nevertheless, due to the capillary rise, the transition from the saturated zone to the unsaturated zone (capillary fringe) is not sharp, especially in fine-textured soils. Indeed, the observed reflection occurs some distance above the water table, depending on the shape of the capillary fringe. Under hydrostatic conditions, the shape corresponds to the soil’s water retention curve [38]; otherwise, it can be relatively variable depending on the hydrodynamic conditions of the soil [148][155][157][158][159][160]. The top of the capillary fringe is partly saturated and the bottom is fully saturated (the bottom is the water table). Thus, there is an SWC variation through the capillary fringe, and GPR wave velocity decreases from top to bottom (εr increases from top to bottom) [115][156][160]. Because of this heterogeneity, GPR wave reflection varies, along with the capillary fringe [148][151][156]. The height of the capillary fringe varies with the texture, pore size, and pore size distribution [148][151][154][156][161]. In coarse grain soils (e.g., sand), the capillary height is less, and the contrast in εr between dry and saturated sand is sharp; consequently, the water table can be distinguished from easily GPR reflections [153][161][162]. Conversely, the capillarity is high in fine-grain soils. Therefore, it is difficult to distinguish the actual water table in clay soils due to low contrast at the interface, decreasing the accuracy of DTWT estimation using GPR [151][157][158][159][160][162][163].

3.6. Other Soil Properties

Other than SWC, soil compaction, and soil salinity, GPR has been applied to estimate other soil properties, such as soil texture and clay content [164][165][166][167] and SOM/soil organic carbon (SOC) [168][169][170][171][172]. Soil profile stratigraphy studies focusing on other soil properties were carried out by Doolittle and Collins [173], Stroh et al. [174], Meadows et al. [164], André et al. [175], and Nováková et al. [176], and soil organic horizons were studied in particular by Winkelbauer et al. [177].
In agricultural soil studies, GPR is extensively used for SWC estimation, followed by the estimation of soil salinity, porosity, and bulk density, while other properties are currently being researched. In addition to soil properties and states, GPR estimates soil horizons, stratigraphy, and water table mapping. The estimation of these properties in the agricultural landscape using GPR will provide essential information needed for farmland management to support PA.

References

  1. Stafford, J.V. Implementing precision agriculture in the 21st century. J. Agric. Eng. Res. 2000, 76, 267–275.
  2. Friedl, M.A. Remote sensing of croplands. In Comprehensive Remote Sensing—Elsevier Earth Systems and Environmental Science; Liang, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 78–95.
  3. Pallottino, F.; Biocca, M.; Nardi, P.; Figorilli, S.; Menesatti, P.; Costa, C. Science mapping approach to analyze the research evolution on precision agriculture: World, EU and Italian situation. Precis. Agric. 2018, 19, 1011–1026.
  4. Aubert, B.A.; Schroeder, A.; Grimaudo, J. IT as enabler of sustainable farming: An empirical analysis of farmers’ adoption decision of precision agriculture technology. Decis. Support Syst. 2012, 54, 510–520.
  5. Nicol, L.A.; Nicol, C.J. Adoption of precision agriculture to reduce inputs, enhance sustainability and increase food production: A study of Southern Alberta, Canada. WIT Trans. Ecol. Environ. 2018, 217, 1743–3541.
  6. Goel, R.K.; Yadav, C.S.; Vishnoi, S.; Rastogi, R. Smart agriculture—Urgent need of the day in developing countries. Sustain. Comput. Inform. Syst. 2021, 30, 100512.
  7. Hammond, M.W.; Mulla, D.J.; Fairchild, D.S. Development of management maps for soil variability. In Proceedings of the 39th Annual Far West Regional Fertilizer Conference, Bozeman, MT, USA, 11–13 July 1988; pp. 67–76.
  8. Mulla, D.J.; Hammond, M.W. Mapping of soil test results from large irrigation circles. In Proceedings of the 39th Annual Far West Regional Fertilizer Conference, Bozeman, MT, USA, 11–13 July 1988; pp. 169–176.
  9. Schmidhalter, U.; Maidl, F.X.; Heuwinkel, H.; Demmel, M.; Auernhammer, H.; Noack, P.O.; Rothmund, M. Precision farming–adaptation of land use management to small scale heterogeneity. In Perspectives for Agroecosystem Management: Balancing Environmental and Socio-Economic Demands; Schröder, P., Pfadenhauer, J., Munch, J.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Chapter 2.3; pp. 121–199.
  10. Pinaki, M.; Tewari, V.K. Present status of precision farming: A review. Int. J. Agric. Res. 2010, 5, 1124–1133.
  11. Mulla, D.; Khosla, R. Historical evolution and recent advances in precision farming. In Soil Specific Farming: Precision Agriculture; Lal, R., Stewart, B.A., Eds.; Taylor and Francis: Boca Raton, FL, USA, 2015; Chapter 1; pp. 1–36.
  12. Alix, A.; Capri, E. Modern agriculture in Europe and the role of pesticides. In Advances in Chemical Pollution, Environmental Management and Protection; Capri, E., Alix, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 2, pp. 1–22.
  13. Kashyap, B.; Kumar, R. Sensing methodologies in agriculture for soil moisture and nutrient monitoring. IEEE Access 2021, 9, 14095–14121.
  14. Bongiovanni, R.; Lowenberg-DeBoer, J. Precision agriculture and sustainability. Precis. Agric. 2004, 5, 359–387.
  15. Hammond, M.W.; Mulla, D.J. Field variation in soil fertility: Its assessment and management for potato production. In Proceedings of the 28th Annual Washington State Potato Conference, Moses Lake, WA, USA, 2 February 1989.
  16. Jarolímek, J.; Stočes, M.; Masner, J.; Vaněk, J.; Šimek, P.; Pavlík, J.; Rajtr, J. User-technological index of precision agriculture. Agris On-Line Pap. Econ. 2017, 9, 69–75.
  17. Shafi, U.; Mumtaz, R.; García-Nieto, J.; Hassan, S.A.; Zaidi, S.A.R.; Iqbal, N. Precision agriculture techniques and practices: From considerations to applications. Sensors 2019, 19, 3796.
  18. Fairchild, D.; Hammond, M. Using computerized fertilizer application equipment for efficient soil fertility management. In Proceedings of the 39th Annual Regional Fertilizer Conference, BoTeman, MT, USA, 11–13 July 1988; Jacobsen, J.S., Ed.; pp. 77–82.
  19. Mulla, D.J. Using geostatistics and spectral analysis to study spatial patterns in the topography of southeastern Washington State, U.S.A. Earth Surf. Process. 1988, 13, 389–405.
  20. Vereecken, H.; Binley, A.; Cassiani, G.; Revil, A.; Titov, K. Applied hydrogeophysics. In Applied Hydrogeophysics: NATO Science Series; Vereecken, H., Binley, A., Cassiani, G., Revil, A., Titov, K., Eds.; Springer Dordrecht: Berlin, Germany, 2006; Volume 71, pp. 1–8.
  21. Rubin, Y.; Hubbard, S.S. Hydrogeophysics; Springer: Cham, Switzerland, 2005; Volume 50.
  22. Lambot, S.; Binley, A.; Slob, E.C.; Hubbard, S. Foreword to the special issue on ground-penetrating radar in hydrogeophysics. Vadose Zone J. 2008, 7, 137–139.
  23. Binley, A.; Cassiani, G.; Deiana, R. Hydrogeophysics: Opportunities and challenges. Boll. Geofis. Teor. Ed Appl. 2010, 51, 267–284.
  24. Vereecken, H.; Hubbard, S.; Binley, A.; Ferre, T. Hydrogeophysics: An introduction from the guest editors. Vadose Zone J. 2004, 3, 1060–1062.
  25. Blazevic, L.A.; Bodet, L.; Pasquet, S.; Linde, N.; Jougnot, D.; Longuevergne, L. Time-lapse seismic and electrical monitoring of the vadose zone during a controlled infiltration experiment at the Ploemeur hydrological observatory, France. Water 2020, 12, 1230.
  26. Hubbard, S.S. Hydrogeophysics; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2011.
  27. Baker, G.S.; Jordan, T.E.; Pardy, J. An introduction to ground penetrating radar (GPR). In Stratigraphic Analyses Using GPR; Baker, G.S., Jol, H.M., Eds.; Geological Society of America: Boulder, CO, USA, 2007; Volume 432, pp. 1–18.
  28. Davis, J.L.; Annan, A.P. Ground penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551.
  29. Reynolds, J.M. An Introduction to Applied and Environmental Geophysics, 2nd ed.; A John Wiley & Sons Ltd.: West Sussex, UK, 2011.
  30. Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring soil water content with ground penetrating radar: A decade of progress. Vadose Zone J. 2018, 17, 1–9.
  31. Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582.
  32. Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491.
  33. Weiler, K.W.; Steenhuis, T.S.; Boll, J.; Kung, K.J.S. Comparison of ground penetrating radar and time-domain reflectometry as soil water sensors. Soil Sci. Soc. Am. J. 1998, 62, 1237–1239.
  34. Knight, R. Ground penetrating radar for environmental applications. Annu. Rev. Earth Planet. Sci. 2001, 29, 229–255.
  35. Annan, A.P. Ground penetrating radar. In Near-Surface Geophysics; Butler, D.K., Ed.; Society of Exploration Geophysics: Tulsa, OK, USA, 2005; pp. 434–557.
  36. Cassidy, N.J. Electrical and magnetic properties of rocks, soils, fluids. In Ground Penetrating Radar Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 2; pp. 41–67.
  37. Sperl, C. Determination of Spatial and Temporal Variation of the Soil Water Content in an Agro-Ecosystem with Ground-Penetrating Radar. Ph.D. Thesis, Technische Universitat München, Munich, Germany, 1999.
  38. Lambot, S.; Rhebergen, J.; van den Bosch, I.; Slob, E.C.; Vanclooster, M. Measuring the soil water content profile of a sandy soil with an off-ground monostatic ground penetrating radar. Vadose Zone J. 2004, 3, 1063–1071.
  39. Zhang, J.; Lin, H.; Doolittle, J. Soil layering and preferential flow impacts on seasonal changes of GPR signals in two contrasting soils. Geoderma 2014, 213, 560–569.
  40. Chew, W.C. Waves and Fields in Inhomogeneous Media; Wiley-IEEE Press: Piscataway, NJ, USA, 1995.
  41. Galagedara, L.W.; Parkin, G.W.; Redman, J.D. An analysis of the ground penetrating radar direct ground wave method for soil water content measurement. Hydrol. Process. 2003, 17, 3615–3628.
  42. Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; Endres, A.L. Assessment of soil moisture content measured by borehole GPR and TDR under transient irrigation and drainage. J. Environ. Eng. Geophys. 2003, 8, 77–86.
  43. Wijewardana, Y.G.N.S.; Galagedara, L.W. Estimation of spatio-temporal variability of soil water content in agricultural fields with ground penetrating radar. J. Hydrol. 2010, 391, 24–33.
  44. Liu, X.; Chen, J.; Cui, X.; Liu, Q.; Cao, X.; Chen, X. Measurement of soil water content using ground penetrating radar: A review of current methods. Int. J. Digit. Earth 2017, 12, 95–118.
  45. Annan, A.P. Electromagnteic principles of ground penetrating radar. In Ground Penetrating Radar Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 3–37.
  46. Chanzy, A.; Tarussov, A.; Bonn, F.; Judge, A. Soil water content determination using a digital ground penetrating radar. Soil Sci. Soc. Am. J. 1996, 60, 1318–1326.
  47. van Overmeeren, R.A.; Sariowan, S.V.; Gehrels, J.C. Ground penetrating radar for determining volumetric soil water content; results of comparative measurements at two test sites. J. Hydrol. 1997, 197, 316–338.
  48. Hubbard, S.; Grote, K.; Rubin, Y. Mapping the volumetric soil water content of a california vineyard using high-frequency GPR ground wave data. Lead. Edge 2002, 21, 552.
  49. Huisman, J.A.; Bouten, W. Accuracy and reproducibility of mapping surface soil water content with the ground wave of ground-penetrating radar. J. Environ. Eng. Geophys. 2003, 8, 67–75.
  50. Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; Von Bertoldi, P.; Endres, A.L. Field studies of the GPR ground wave method for estimating soil water content during irrigation and drainage. J. Hydrol. 2005, 301, 182–197.
  51. Galagedara, L.W.; Parkin, G.W.; Redman, J.D. Measuring and modeling of direct ground wave depth penetration under transient soil moisture conditions. Subsurf. Sens. Technolo. Appli. 2005, 6, 193–205.
  52. Illawathure, C.; Parkin, G.; Lambot, S.; Galagedara, L. Evaluating soil moisture estimation from ground-penetrating radar hyperbola fitting with respect to a systematic time-domain reflectometry data collection in a boreal podzolic agricultural field. Hydrol. Process. 2020, 34, 1428–1445.
  53. Grote, K.; Hubbard, S.; Rubin, Y. Field-scale estimation of volumetric water content using ground penetrating radar ground wave techniques. Water Resour. Res. 2003, 39, 1–14.
  54. Wollschläger, U.; Roth, K. Estimation of temporal changes of volumetric soil water content from ground-penetrating radar reflections. Subsurf. Sens. Technol. Appli. 2005, 6, 207–218.
  55. Lu, Y.; Song, W.; Lu, J.; Wang, X.; Tan, Y. An examination of soil moisture estimation using ground penetrating radar in desert steppe. Water 2017, 9, 521.
  56. Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269.
  57. Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744.
  58. Stoffregen, H.; Zenker, T.; Wessolek, G. Accuracy of soil water content measurements using ground penetrating radar: Comparison of ground penetrating radar and lysimeter data. J. Hydrol. 2002, 267, 201–206.
  59. Loeffler, O.; Bano, M. Ground penetrating radar measurements in a controlled vadose zone: Influence of the water content. Vadose Zone J. 2004, 3, 1082–1092.
  60. Zhou, L.; Yu, D.; Wang, Z.; Wang, X. Soil water content estimation using high-frequency ground penetrating radar. Water 2019, 11, 1036.
  61. Cui, X.; Guo, L.; Chen, J.; Chen, X.; Zhu, X. Estimating tree-root biomass in different depths using ground-penetrating radar: Evidence from a controlled experiment. IEEE Trans. Geosci. Remote Sens. 2019, 51, 3410–3423.
  62. Liu, X.; Cui, X.; Guo, L.; Chen, J.; Li, W.; Yang, D.; Cao, X.; Chen, X.; Liu, Q.; Lin, H. Non-invasive estimation of root zone soil moisture from coarse root reflections in ground-penetrating radar images. Plant Soil 2019, 436, 623–639.
  63. Sham, J.F.C.; Lai, W.W.-L.; Leung, C.H.C. Effects of homogeneous/heterogeneous water distribution on GPR wave velocity in a soil’s wetting and drying process. In Proceedings of the 16th International Conference on Ground Penetrating Radar, Hong Kong, China, 13–16 June 2016; IEEE: Manhattan, NY, USA, 2016; pp. 1–6.
  64. Steelman, C.M.; Endres, A.L. Assessing vertical soil moisture dynamics using multi-frequency GPR common-midpoint soundings. J. Hydrol. 2012, 436–437, 51–66.
  65. Huisman, J.A.; Sperl, C.; Bouten, W.; Verstraten, J.M. Soil water content measurements at different scales: Accuracy of time domain reflectometry and ground-penetrating radar. J. Hydrol. 2001, 245, 48–58.
  66. Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Monitoring temporal development of spatial soil water content variation: Comparison of ground penetrating radar and time domain reflectometry. Vadose Zone J. 2003, 2, 519–529.
  67. Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: Comparison of ground-penetrating radar and time domain reflectometry. J. Hydrol. 2002, 269, 194–207.
  68. Grote, K.; Anger, C.; Kelly, B.; Hubbard, S.; Rubin, Y. Characterization of soil water content variability and soil texture using GPR groundwave techniques. J. Environ. Eng. Geophys. 2010, 15, 93–110.
  69. Minet, J.; Bogaert, P.; Vanclooster, M.; Lambot, S. Validation of ground penetrating radar full-waveform inversion for field scale soil moisture mapping. J. Hydrol. 2012, 424, 112–123.
  70. Ardekani, M.R.M. Off- and on-ground GPR techniques for field-scale soil moisture mapping. Geoderma 2013, 200–201, 55–66.
  71. Thitimakorn, T.; Kummode, S.; Kupongsak, S. Determination of spatial and temporal variations of volumetric soil water content using ground penetrating radar: A case study in Thailand. Appl. Environ. Res. 2016, 38, 33–46.
  72. Cao, Q.; Song, X.; Wu, H.; Gao, L.; Liu, F.; Yang, S.; Zhang, G. Mapping the response of volumetric soil water content to an intense rainfall event at the field scale using GPR. J. Hydrol. 2020, 583, 124605.
  73. Weihermüller, L.; Huisman, J.A.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques. J. Hydrol. 2007, 340, 205–216.
  74. Pallavi, B.; Saito, H.; Kato, M. Application of GPR ground wave for mapping of spatiotemporal variations in the surface moisture content at a natural field site. In Proceedings of the 19th World Congress of Soil Science: Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010; Gilkes, R.J., Prakougkep, N., Eds.; Australian Society of Soil Science: Warragul, Australia, 2010; pp. 13–16.
  75. Galagedara, L.W.; Redman, J.D.; Parkin, G.W.; Annan, A.P.; Endres, A.L. Numerical modeling of GPR to determine the direct ground wave sampling depth. Vadose Zone J. 2005, 4, 1096–1106.
  76. Pallavi, B.; Saito, H.; Kato, M. Estimating depth of influence of GPR ground wave in lysimeter experiment. J. Arid. Land Stud. 2009, 19, 121–124.
  77. Binley, A.; Winship, P.; West, L.J.; Pokar, M.; Middleton, R. Seasonal variation of moisture content in unsaturated sandstone inferred from borehole radar and resistivity profiles. J. Hydrol. 2002, 267, 160–172.
  78. Strobach, E.; Harris, B.D.; Dupuis, J.C.; Kepic, A.W. Time-lapse borehole radar for monitoring rainfall infiltration through podosol horizons in a sandy vadose zone. Water Resour. Res. 2014, 50, 2140–2163.
  79. Klotzsche, A.; Lärm, L.; Vanderborght, J.; Cai, G.; Morandage, S.; Zörner, M.; Vereecken, H.; Kruk, J. Monitoring soil water content using time-lapse horizontal borehole GPR data at the field-plot scale. Vadose Zone J. 2019, 18, 190044.
  80. Yu, Y.; Klotzsche, A.; Weihermüller, L.; Huisman, J.A.; Vanderborght, J.; Vereecken, H.; van der Kruk, J. Measuring vertical soil water content profiles by combining horizontal borehole and dispersive surface ground penetrating radar data. Near Surf. Geophys. 2020, 18, 275–294.
  81. Rucker, D.F.; Ferré, T.P.A. Near-surface water content estimation with borehole ground penetrating radar using critically refracted waves. Vadose Zone J. 2003, 2, 247–252.
  82. Rucker, D.F.; Ferré, T.P.A. Correcting water content measurement errors associated with critically refracted first arrivals on zero offset profiling borehole ground penetrating radar profiles. Vadose Zone J. 2004, 3, 278–287.
  83. Rucker, D.F.; Ferré, T.P.A. Automated water content reconstruction of zero-offset borehole ground penetrating radar data using simulated annealing. J. Hydrol. 2005, 309, 1–16.
  84. Lambot, S.; Weihermüller, L.; Huisman, J.A.; Vereecken, H.; Vanclooster, M.; Slob, E.C. Analysis of air-launched ground-penetrating radar techniques to measure the soil surface water content. Water Resour. Res. 2006, 42, W11403.
  85. al Hagrey, S.A.; Müller, C. GPR study of pore water content and salinity in sand. Geophys. Prospect. 2000, 48, 63–85.
  86. Redman, J.D.; Davis, J.L.; Galagedara, L.W.; Parkin, G.W. Field studies of GPR air launched surface reflectivity measurements of soil water content. In Proceedings of the 9th International Conference on Ground Penetrating Radar, Santa Barbara, CA, USA, 29 April–2 May 2002; Koppenjan, S.K., Lee, H., Eds.; SPIE: Bellingham, WA, USA, 2002; Volume 4758, pp. 156–161.
  87. Redman, D.; Galagedara, L.; Parkin, G. Measuring soil water content with the ground penetrating radar surface reflectivity method: Effects of spatial variability. In Proceedings of the 2003 ASABE Annual Meeting (Paper 032276), Las Vegas, NV, USA, 27 July 2003; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2003.
  88. Pettinelli, E.; Vannaroni, G.; Di Pasquo, B.; Mattei, E.; Di Matteo, A.; De Santis, A.; Annan, A.P. Correlation between near-surface electromagnetic soil parameters and early-time GPR signals: An experimental study. Geophysics 2007, 72, A25–A28.
  89. Pettinelli, E.; Di Matteo, A.; Beaubien, S.E.; Mattei, E.; Lauro, S.E.; Galli, A.; Vannaroni, G. A controlled experiment to investigate the correlation between early-time signal attributes of ground-coupled radar and soil dielectric properties. J. Appl. Geophys. 2014, 101, 68–76.
  90. Algeo, J.; Van Dam, R.L.; Slater, L. Early-time GPR: A method to monitor spatial variations in soil water content during irrigation in clay soils. Vadose Zone J. 2016, 15, 1–9.
  91. Ferrara, C.; Barone, P.M.; Steelman, C.M.; Pettinelli, E.; Endres, A.L. Monitoring shallow soil water content under natural field conditions using the early-time GPR signal technique. Vadose Zone J. 2013, 12, 1–9.
  92. Ferrara, C.; Barone, P.M.; Mattei, E.; Galli, A.; Comite, D.; Lauro, S.E.; Vannaroni, G.; Pettinelli, E. An evaluation of the early-time GPR amplitude technique for electrical conductivity monitoring. In Proceedings of the IWAGPR 2013—7th International Workshop on Advanced Ground Penetrating Radar, Nantes, France, 2–5 July 2013; IEEE: Manhattan, NY, USA, 2013; pp. 1–4.
  93. Algeo, J.; Slater, L.; Binley, A.; Van Dam, R.L.; Watts, C. A comparison of ground-penetrating radar early-time signal approaches for mapping changes in shallow soil water content. Vadose Zone J. 2018, 17, 1–11.
  94. Ernst, J.R.; Green, A.G.; Maurer, H.; Holliger, K. Application of a new 2D timedomain full-waveform inversion scheme to crosshole radar data. Geophysics 2007, 72, J53–J64.
  95. Klotzsche, A.; van der Kruk, J.; Meles, G.A.; Doetsch, J.; Maurer, H.; Linde, N. Full-waveform inversion of crosshole groundpenetrating radar data to characterize a gravel aquifer close to the Thur River, Switzerland. Near Surf. Geophys. 2010, 8, 635–649.
  96. Meles, G.A.; van der Kruk, J.; Greenhalgh, S.A.; Ernst, J.R.; Maurer, H.; Green, A.G. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3391–3407.
  97. Klotzsche, A.; van der Kruk, J.; Bradford, J.; Vereecken, H. Detection of spatially limited highporosity layers using crosshole GPR signal analysis and full-waveform inversion. Water Resour. Res. 2014, 50, 6966–6985.
  98. Gueting, N.; Vienken, T.; Klotzsche, A.; van der Kruk, J.; Vanderborght, J.; Caers, J.; Vereecken, H.; Englert, A. High resolution aquifer characterization using crosshole GPR full-waveform tomography: Comparison with direct-push and tracer test data. Water Resour. Res. 2017, 53, 49–72.
  99. Yu, Y.; Huisman, J.A.; Klotzsche, A.; Vereecken, H.; Weihermüller, L. Coupled full-waveform inversion of horizontal borehole ground penetrating radar data to estimate soil hydraulic parameters: A synthetic study. J. Hydrol. 2022, 610, 127817.
  100. Lambot, S.; Slob, E.; Chavarro, D.; Lubczynski, M.; Vereecken, H. Measuring soil surface water content in irrigated areas of southern Tunisia using full-waveform inversion of proximal GPR data. Near Surf. Geophys. 2008, 6, 403–410.
  101. Lambot, S.; André, F. Full-wave modeling of near-field radar data for planar layered media reconstruction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2295–2303.
  102. Jonard, F.; Weihermuller, L.; Jadoon, K.Z.; Schwank, M.; Vereecken, H.; Lambot, S. Mapping field-scale soil moisture with L-band radiometer and ground-penetrating radar over bare soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2863–2875.
  103. Jonard, F.; Weihermüller, J.; Vereecken, H.; Lambot, S. Accounting for soil surface roughness in the inversion of ultrawideband offground GPR signal for soil moisture retrieval. Geophysics 2012, 77, H1–H7.
  104. de Mahieu, A.; Ponette, Q.; Mounir, F.; Lambot, S. Using GPR to analyze regeneration success of cork oaks in the Maâmora forest (Morocco). NDT E Int. 2020, 115, 102297.
  105. Wu, K.; Lambot, S. Analysis of low-frequency drone-borne GPR for root-zone soil electrical conductivity characterization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2006213.
  106. Tran, A.P.; Vanclooster, M.; Lambot, S. Improving soil moisture profile reconstruction from ground-penetrating radar data: A maximum likelihood ensemble filter approach. Hydrol. Earth Syst. Sci. 2013, 17, 2543–2556.
  107. De Coster, A.; Tran, A.P.; Lambot, S. Fundamental analyses on layered media reconstruction using GPR and full-wave inversion in near-field conditions. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5143–5158.
  108. Wu, K.; Desesquelles, H.; Cockenpot, R.; Guyard, L.; Cuisiniez, V.; Lambot, S. Ground-penetrating radar full-wave inversion for soil moisture mapping in Trench-Hill potato fields for precise irrigation. Remote Sens. 2022, 14, 6046.
  109. Lambot, S.; Slob, E.C.; van den Bosch, I.; Stockbroeckx, B.; Vanclooster, M. Modeling of ground-penetrating radar for accurate characterization of subsurface electric properties. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2555–2568.
  110. Turesson, A. Water content and porosity estimated from ground-penetrating radar and resistivity. J. Appl. Geophy. 2006, 58, 99–111.
  111. Lai, W.L.; Tsang, W.F.; Fang, H.; Xiao, D. Experimental determination of bulk dielectric properties and porosity of porous asphalt and soils using GPR and a cyclic moisture variation technique. Geophysics 2006, 71, K93.
  112. Nimmo, J.R. Porosity and pore size distribution. Ency. Soils Environ. 2001, 3, 295–303.
  113. Ghose, R.; Slob, E.C. Quantitative integration of seismic and GPR reflections to derive unique estimates for water saturation and porosity in subsoil. Geophys. Res. Lett. 2006, 33, 2–5.
  114. Khalil, M.A.; Hafez, M.A.; Santos, F.M.; Ramalho, E.C.; Mesbah, H.S.A.; El-Qady, G.M. An approach to estimate porosity and groundwater salinity by combined application of GPR and VES: A case study in the Nubian sandstone aquifer. Near Surf. Geophys. 2010, 8, 223–233.
  115. Hillel, D. Environmental Soil Physics; Academic Press: San Diego, CA, USA, 1998.
  116. Bradford, J.H.; Clement, W.P.; Barrash, W. Estimating porosity with ground-penetrating radar reflection tomography: A controlled 3-D experiment at the boise hydrogeophysical research site. Water Resour. Res. 2009, 46, 1–11.
  117. Mount, G.J.; Comas, X. Estimating porosity and solid dielectric permittivity in the Miami Limestone using high-frequency ground penetrating radar (GPR) measurements at the laboratory scale. Water Resour. Res. 2014, 50, 7590–7605.
  118. Akinsunmade, A.; Tomecka-Suchoń, S.; Pysz, P. Correlation between agrotechnical properties of selected soil types and corresponding GPR response. Acta Geophys. 2019, 67, 1913–1919.
  119. Akinsunmade, A. GPR imaging of traffic compaction effects on soil structures. Acta Geophys. 2021, 69, 643–653.
  120. Akinsunmade, A.; Tomecka-Suchoń, S.; Kiełbasa, P.; Juliszewski, T.; Pysz, P.; Karczewski, J.; Zagórda, M. GPR geophysical method as a remediation tool to determine zones of high penetration resistance of soil. J. Phys. Conf. Ser. 2021, 1782, 012001.
  121. Wang, P.; Hu, Z.; Zhao, Y.; Li, X. Experimental study of soil compaction effects on GPR signals. J. Appl. Geophys. 2016, 126, 128–137.
  122. Jonard, F.; Mahmoudzadeh, M.; Roisin, C.; Weihermüller, L.; André, F.; Minet, J.; Lambot, S. Characterization of tillage effects on the spatial variation of soil properties using ground-penetrating radar and electromagnetic induction. Geoderma 2013, 207, 310–322.
  123. Muñiz, E.; Shaw, R.K.; Gimenez, D.; Williams, C.A.; Kenny, L. Use of ground-penetrating radar to determine depth to compacted layer in soils under pasture. In Digital Soil Morphometrics; Hartemink, A.E., Minasny, B., Eds.; Springer Nature: Cham, Switzerland, 2016; pp. 411–421.
  124. Saarenketo, T. Electrical properties of water in clay and silty soils. J. Appl. Geophys. 1998, 40, 73–88.
  125. Awak, E.A.; George, A.M.; Urang, J.G.; Udoh, J.T. Determination of soil electrical conductivity using ground penetrating radar (GPR) for precision agriculture. Int. J. Sci. Eng. Res. 2017, 8, 1971–1977.
  126. Corwin, D.L.; Scudiero, E. Review of soil salinity assessment for agriculture across multiple scales using proximal and/or remote sensors. In Advances in Agronomy; Sparks, D.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 158, pp. 1–130.
  127. Miller, J.J.; Curtain, D. Electrical conductivity and soluble ions. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press, Taylor & Francis Group: Oxfordshire, UK, 2008; pp. 161–171.
  128. Corwin, D.L.; Lesch, S.M. Application of soil electrical conductivity to precision agriculture: Theory, principles, and guidelines. Agron. J. 2003, 95, 455–471.
  129. Corwin, D.L.; Lesch, S.M. Apparent soil electrical conductivity measurements in agriculture. Comput. Electron. Agric. 2005, 46, 11–43.
  130. Altdorff, D.; Galagedara, L.; Nadeem, M.; Cheema, M.; Unc, A. Effect of agronomic treatments on the accuracy of soil moisture mapping by electromagnetic induction. Catena 2018, 164, 96–106.
  131. Badewa, E.; Unc, A.; Cheema, M.; Kavanagh, V.; Galagedara, L. Soil moisture mapping using multi-frequency and multi-coil electromagnetic induction sensors on managed podzols. Agronomy 2018, 8, 224.
  132. Badewa, E.; Unc, A.; Cheema, M.; Galagedara, L. Temporal stability of soil apparent electrical conductivity (ECa) in managed podzols. Acta Geophys. 2019, 67, 1107–1118.
  133. Wu, B.; Li, X.; Zhao, K.; Jiang, T.; Zheng, X.; Li, X.; Gu, L.; Wang, X. A nondestructive conductivity estimating method for saline-alkali land based on ground penetrating radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2605–2614.
  134. Rhoades, J.D.; Corwin, D.L.; Lesch, S.M. Geospatial measurements of soil electrical conductivity to assess soil salinity and diffuse salt loading from irrigation. In Geophysical Monograph Series: Assessment of Non-Point Source Pollution in the Vadose Zone; Corwin, D.L., Loague, K., Ellsworth, T.R., Eds.; American Geophysical Union: Washington, DC, USA, 1998; Volume 108, pp. 197–215.
  135. Mimrose, D.M.C.S.; Galagedara, L.W.; Parkin, G.W.; Wijewardana, Y.G.N.S. Investigating the effect of electrical conductivity in irrigation water on reflected wave energy of GPR. Trop. Agric. 2011, 159, 29–46.
  136. Alsharahi, G.; Driouach, A.; Faize, A. Performance of GPR influenced by electrical conductivity and dielectric constant. Proc. Technol. 2016, 22, 570–575.
  137. Wijewardana, N.S.; Galagedara, L.W.; Mowjood, M.I.M. Assessment of groundwater contamination by landfill leachate with ground penetrating radar. In Proceedings of the 14th International Conference on Ground Penetrating Radar, Shanghai, China, 4–8 June 2012; pp. 728–732.
  138. Wijewardana, Y.N.S.; Galagedara, L.W.; Mowjood, M.I.M.; Kawamoto, K. Assessment of inorganic pollutant contamination in groundwater using ground penetrating radar (GPR). Trop. Agric. Res. 2015, 26, 700–706.
  139. Wijewardana, Y.N.S.; Shilpadi, A.T.; Mowjood, M.I.M.; Kawamoto, K.; Galagedara, L.W. Ground-penetrating radar (GPR) responses for sub-surface salt contamination and solid waste: Modeling and controlled lysimeter studies. Environ. Monit. Assess. 2017, 189, 57.
  140. Tsoflias, G.P.; Becker, M.W. Ground-penetrating-radar response to fracture-fluid salinity: Why lower frequencies are favorable for resolving salinity changes. Geophysics 2008, 73, J25–J30.
  141. Zhang, M.; Feng, X.; Bano, M.; Xing, H.; Wang, T.; Liang, W.; Zhou, H.; Dong, Z.; An, Y.; Zhang, Y. Review of ground penetrating radar applications for water dynamics studies in unsaturated zone. Remote Sens. 2022, 14, 5993.
  142. Di Prima, S.; Winiarski, T.; Angulo-Jaramillo, R.; Stewart, R.D.; Castellini, M.; Abou Najm, M.R.; Ventrella, D.; Pirastru, M.; Giadrossich, F.; Capello, G.; et al. Detecting infiltrated water and preferential flow pathways through time-lapse ground-penetrating radar surveys. Sci. Total Environ. 2010, 726, 138511.
  143. Jury, W.A.; Gardner, W.R.; Gardner, W.H. Soil Physics, 5th ed.; John Wiley: Hoboken, NY, USA, 1991.
  144. Cassiani, G.; Binley, A. Modeling unsaturated flow in a layered formation under quasi-steady state conditions using geophysical data constraints. Adv. Water Resour. 2005, 28, 467–477.
  145. Kowalsky, M.B.; Finsterle, S.; Peterson, J.; Hubbard, S.; Rubin, Y.; Majer, E.; Ward, A.; Gee, G. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data. Water Resour. Res. 2005, 41.
  146. Jadoon, K.Z.; Slob, E.; Vanclooster, M.; Vereecken, H.; Lambot, S. Uniqueness and stability analysis of hydrogeophysical inversion for time-lapse ground penetrating radar estimates of shallow soil hydraulic properties. Water Resour. Res. 2008, 44, W09421.
  147. Jadoon, K.Z.; Weihermuller, L.; Scharnagl, B.; Kowalsky, M.B.; Bechtold, M.; Hubbard, S.S.; Vereecken, H.; Lambot, S. Estimation of soil hydraulic parameters in the field by integrated hydrogeophysical inversion of time-lapse ground-penetrating radar data. Vadose Zone J. 2012, 11.
  148. Igel, J.; Stadler, S.; Guenther, T. High-resolution investigation of the capillary transition zone and its influence on GPR signatures. In Proceedings of the 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; IEEE: Manhattan, NY, USA, 2016; pp. 1–5.
  149. Essam, D.; Ahmed, M.; Abouelmagd, A.; Soliman, F. Monitoring temporal variations in groundwater levels in urban areas using ground penetrating radar. Sci. Total Environ. 2020, 703, 134986.
  150. van Overmeeren, R.A. Radar facies of unconsolidated sediments in The Netherlands: A radar stratigraphic interpretation method for hydrogeology. J. Appl. Geophys. 1998, 40, 1–18.
  151. Doolittle, J.A.; Jenkinson, B.; Hopkins, D.; Ulmer, M.; Tuttle, W. Hydropedological investigations with ground-penetrating radar (GPR): Estimating water-table depths and local ground-water flow pattern in areas of coarse-textured soils. Geoderma 2006, 131, 317–329.
  152. Mahmoudzadeh, M.R.; Frances, A.P.; Lubczynski, M.; Lambot, S. Using ground penetrating radar to investigate the water table depth in weathered granites—Sardon case study, Spain. J. Appl. Geophys. 2012, 79, 17–26.
  153. Paz, C.; Alcalá, F.J.; Carvalho, J.M.; Ribeiro, L. Current uses of ground penetrating radar in groundwater-dependent ecosystems research. Sci. Total Environ. 2017, 595, 868–885.
  154. Nguyen, B.L.; Bruining, J.; Slob, E.C.; Hopman, V. Delineation of air/water capillary transition zone from GPR data. SPE Reserv. Eng. 1998, 1, 319–324.
  155. Onishi, K.; Rokugawa, S.; Katoh, Y.; Tokunaga, T. Influence of capillary fringe on the groundwater survey using ground-penetrating radar. ASEG Ext. Abstr. 2004, 1, 1–4.
  156. Bano, M. Effects of the transition zone above a water table on the reflection of GPR waves. Geophys. Res. Lett. 2006, 33, L13309.
  157. Illawathure, C.; Cheema, M.; Kavanagh, V.; Galagedara, L. Distinguishing capillary fringe reflection in a GPR profile for precise water table depth estimation in a boreal podzolic soil field. Water 2020, 12, 1670.
  158. Endres, A.L.; Clement, W.P.; Rudolph, D.L. Ground penetrating radar imaging of an aquifer during a pumping test. Ground Water 2000, 38, 566–576.
  159. Bentley, L.R.; Trenholm, N.M. The accuracy of water table elevation estimates determined from ground penetrating radar data. J. Environ. Eng. Geophys. 2002, 7, 37–53.
  160. Daniels, J.J.; Allred, B.; Binley, A.; Labrecque, D.; Alumbaugh, D. Hydrogeophysical case studies in the vadose zone. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Basel, Switzerland, 2005; Volume 50, pp. 413–440.
  161. Costall, R.; Harris, B.D.; Teo, B.; Schaa, R.; Wagner, F.M.; Pigois, J.P. Groundwater throughflow and seawater intrusion in high quality coastal aquifers. Sci. Rep. 2020, 10, 9866.
  162. Kowalczyk, S.; Lejzerowicz, A.; Kowalczyk, B. Groundwater table level changes based on ground penetrating radar images: A case study. In Proceedings of the 17th International Conference on Ground Penetrating Radar, Rapperswil, Switzerland, 18–21 June 2018; IEEE: Manhattan, NY, USA, 2018; pp. 1–4.
  163. Annan, A.P.; Cosway, S.W.; Redman, J.D. Water table detection with ground-penetrating radar. In SEG Technical Program Expanded Abstracts 1991; Society of Exploration Geophysicists: Houston, TX, USA, 1991; pp. 494–496.
  164. Meadows, D.G.; Young, M.H.; McDonald, E.V. Estimating the fine soil fraction of desert pavements using ground penetrating radar. Vadose Zone J. 2006, 5, 720–730.
  165. De Benedetto, D.; Castrignano, A.; Sollitto, D.; Modugno, F.; Buttafuoco, G.; lo Papa, G. Integrating geophysical and geostatistical techniques to map the spatial variation of clay. Geoderma 2012, 171, 53–63.
  166. Benedetto, F.; Tosti, F. GPR spectral analysis for clay content evaluation by the frequency shift method. J. Appl. Geophys. 2013, 97, 89–96.
  167. Tosti, F.; Patriarca, C.; Slob, E.; Benedetto, A.; Lambot, S. Clay content evaluation in soils through GPR signal processing. J. Appl. Geophys. 2013, 97, 69–80.
  168. van Dam, R.L.; van den Berg, E.H.; van Heteren, S.; Kasse, C.; Kenter, J.A.M.; Groen, K. Influence of Organic Matter in Soils on Radar-Wave Reflection: Sedimentological Implications. J. Sediment. Res. 2002, 72, 341–352.
  169. Comas, X.; Terry, N.; Hribljan, J.A.; Lilleskov, E.A.; Suarez, E.; Chimner, R.A.; Kolka, R.K. Estimating belowground carbon stocks in peatlands of the Ecuadorian paramo using ground penetrating radar (GPR). J. Geophys. Res. 2017, 122, 370–386.
  170. Shen, X.; Foster, T.; Baldi, H.; Dobreva, I.; Burson, B.; Hays, D.; Tabien, R.; Jessup, R. Quantification of soil organic carbon in biochar-amended soil using ground penetrating radar (GPR). Remote Sens. 2019, 11, 2874.
  171. De Benedetto, D.; Barca, E.; Castellini, M.; Popolizio, S.; Lacolla, G.; Stellacci, A.M. Prediction of soil organic carbon at field scale by regression kriging and multivariate adaptive regression splines using geophysical covariates. Land 2022, 11, 381.
  172. Ryazantsev, P.A.; Hartemink, A.E.; Bakhmet, O.N. Delineation and description of soil horizons using ground-penetrating radar for soils under boreal forest in Central Karelia (Russia). Catena 2022, 214, 106285.
  173. Doolittle, J.A.; Collins, M.E. A comparison of EM induction and GPR methods in areas of karst. Geoderma 1998, 85, 83–102.
  174. Stroh, J.C.; Archer, S.; Doolittle, J.A.; Wilding, L. Detection of edaphic discontinuities with ground-penetrating radar and electromagnetic induction. Landsc. Ecol. 2001, 16, 377–390.
  175. André, F.; van Leeuwen, C.; Saussez, S.; Van Durmen, R.; Bogaert, P.; Moghadas, D.; de Rességuier, L.; Delvaux, B.; Vereecken, H.; Lambot, S. High-resolution imaging of a vineyard in south of France using ground-penetrating radar, electromagnetic induction and electrical resistivity tomography. J. Appl. Geophys. 2012, 78, 113–122.
  176. Nováková, E.; Karous, M.; Zajíček, A.; Karousová, M. Evaluation of ground penetrating radar and vertical electrical sounding methods to determine soil horizons and bedrock at the locality Dehtáře. Soil Water Res. 2013, 8, 105–112.
  177. Winkelbauer, J.; Völkel, J.; Leopold, M.; Bernt, N. Methods of surveying the thickness of humous horizons using ground penetrating radar (GPR): An example from the Garmisch-Partenkirchen area of the Northern Alps. Eur. J. For. Res. 2011, 130, 799–812.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Soil Science; Geochemistry & Geophysics; Environmental Sciences
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Sashini Pathirana
,
Sébastien Lambot
,
Manokarajah Krishnapillai
,
Mumtaz Cheema
,
Christina Smeaton
,
Lakshman Galagedara
View Times: 7.9K
Revisions: 3 times (View History)
Update Date: 14 Jun 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback