Population-Based Deep Reinforcement Learning

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Weifan Long	--	3203	2023-05-25 11:23:05	\|
2	format	Jason Zhu	Meta information modification	3203	2023-05-26 04:04:17	\| \|
3	format	Jason Zhu	Meta information modification	3203	2023-06-15 05:38:34	\|

This entry is adapted from the peer-reviewed paper 10.3390/math11102234

Many real-world applications can be described as large-scale games of imperfect information, which require extensive prior domain knowledge, especially in competitive or human–AI cooperation settings. Population-based training methods have become a popular solution to learn robust policies without any prior knowledge, which can generalize to policies of other players or humans.

reinforcement learning multi-agent reinforcement learning self play

1. Introduction

In recent years, PB-DRL has emerged as a promising research direction in the field of DRL. The key idea behind PB-DRL is to employ multiple agents or learners that interact with their environment in parallel and exchange information to improve their performance. This approach has shown great potential in achieving superior results compared to traditional single-agent methods.

2. Naive Self-Play

Self-play (SP) is an open-ended learning training scheme that trains by playing against a mirrored copy of itself without any supervision in various stochastic environments. Compared with expert opponents, SP has shown more amazing performance in many complex problems. The simplest and most effective SP method is naive self-play, first proposed in ^[1]. As shown in Figure 1, the opponent (mirrored agent) uses the same policy network, i.e., the opponent downloads the latest policy network while the agent updates its policy network. Denote

π

as a policy being trained, $π^{zoo}$ as a policy zoo, $π^{'}$ as the policy set of the opponents, $Ω$ as the policy sampling distribution, and G as the gating function for $π^{zoo}$ ^[2]. The policy sampling distribution $Ω$ is

Ω (π^{'} | π^{zoo}, π) = \{\begin{matrix} 1, \forall π^{'} \in π^{zoo} : π^{'} = π \\ 0 . O t h e r w i s e \end{matrix}

Since the policy zoo $π^{zoo}$ only keeps the latest version of policy $π$ , it always clears the old policies $π^{zoo}$ and inserts $π$ , $π^{zoo} = π$ .

Figure 1. Overview of naive self-play.

A variety of works have followed this method since naive self-play is simple and effective. TD-Gammon ^[3] features naive SP to learn a policy by using TD(

λ

) algorithm. At that time, this outperforms supervised learning with expert experience. AlphaGo ^[4] defeated the world champion of Go in 2017; it uses a combination of supervised learning on expert datasets and SP technology. SP is used to update the policy and to generate more data. SP-based applications have been developed rapidly in both academia and industry. One year after AlphaGo, AlphaZero ^[5] gained prominence. In contrast to AlphaGo, AlphaZero does not require domain-specific human knowledge but achieves outstanding performance. Instead, it learns the game policy by playing against itself, using only the game rules.

Naive SP is also a solution for handling many-to-many environments, as demonstrated by JueWu ^[6] which uses this approach for two players controlling five heroes in Honor of Kings during lineup and random lineup stages. Another study applied naive SP to an open-ended environment (hide-and-seek ^[7]), showing that it can lead to emergent auto-curricula with many distinct and compounding phase shifts in agent strategy.

Despite its effectiveness, naive SP may not be sufficient to learn a robust policy due to the lack of diversity in opponent policies. Fictitious self-play is a solution to this problem, where the agent plays against a mixture of its previous policies and fictional policies that are generated by sampling from a distribution over policies learned during training.

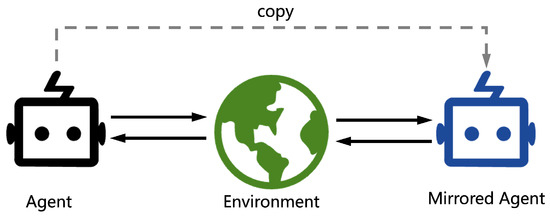
3. Fictitious Self-Play

Fictitious play, introduced by Brown ^[8], is a popular method for learning Nash equilibrium in normal-form games. The premise is that players repeatedly play a game and choose the best response to a uniform mixture of all previous policies at each iteration. As shown in Figure 2, fictitious self-play (FSP) ^[9] is a machine learning framework that implements generalized weakened fictitious play in behavioral strategies in a sample-based fashion. It can avoid cycles by playing against all previous policies. FSP iteratively samples episodes of the game from SP. These episodes constitute datasets that are used by reinforcement learning to compute approximate best responses and by supervised learning to compute perturbed models of average strategies.

Figure 2. Overview of fictitious self-play.

Neural fictitious self-play (NFSP) ^[10] combines FSP with neural network function approximation. NFSP keeps two kinds of memories. One, denoted as

M_{R L}

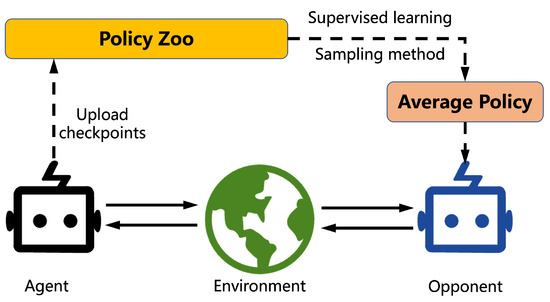
, was used for storing experience of game transitions, while the other, $M_{S L}$ , stored the best response behavior. Each agent computed an approximate best response $β$ from $M_{R L}$ and updated its average policy $Π$ by supervised learning from $M_{S L}$ . In principle, each agent could learn the best response by playing against the average policies of other agents. However, the agent cannot get its best response policy $β$ , which is needed to train its average policy $Π$ , and its average policy $Π$ is needed for the best response training of other agents. NFSP uses the approximation of anticipatory dynamics of continuous-time dynamic fictitious play ^[11], in which players choose the best response to the short-term predicted average policy of their opponents, $Π_{t}^{- i} + η \frac{d}{d t} Π_{t}$ , where $η$ is the anticipatory parameter. NFSP assumes $β_{t + 1} - Π_{t} \approx \frac{d}{d t} Π_{t}$ as a discrete-time approximation. During play, all agents mixed their actions according to $σ = Π + η (β - Π)$ . By using this approach, each agent could learn an approximate best response with predicted average policies of its opponents. In other words, the policy sampling distribution of all agents $Ω$ is

Ω (π) = \{\begin{matrix} β, w i t h p r o b a b i l i t y η \\ Π . w i t h p r o b a b i l i t y 1 - η \end{matrix}

$M_{R L}$ uses a circular buffer to store transition in every step, but $M_{S L}$ only inserts transition while agent follows the best response policy $β$ .

The Exploitability Descent (ED) algorithm ^[12] is a PB-DRL method that directly optimizes policies against worst-case opponents without the need to compute average policies. In contrast to NFSP algorithm, which requires a large reservoir buffer to compute an approximate equilibrium, ED focuses on decreasing the “exploitability” of each player, which refers to how much a player could gain by switching to a best response. The algorithm has two steps for each player on each iteration. The first step is identical to the FP algorithm, where the best response to the policy of each player is computed. The second step performs gradient ascent on the policy to increase the utility of each player against the respective best responder, aiming to decrease the exploitability of each player. In a tabular setting with Q-values and L2 projection, the policy gradient ascent update is defined by equation

\begin{matrix} θ_{S}^{t} & = P_{ℓ_{2}} (θ_{S}^{t - 1} + α^{t} 〈 \nabla_{θ_{S}} {π_{θ}}^{t - 1} (S), Q^{b} (S) 〉) \\ = P_{ℓ_{2}} (θ_{S}^{t - 1} + α^{t} Q^{b} (S)), \end{matrix}

where $Q^{b} (S)$ is the expected return at state S with joint policy set $b$ , $P_{ℓ_{2}}$ is the L2 projection, $\nabla_{θ_{S}} {π_{θ}}^{t - 1} (S)$ is an identity matrix, and $α$ is the step size. In other words, the ED algorithm directly optimizes policies against worst-case opponents, making it a promising approach for addressing games with complex strategy spaces.

A related approach from another perspective is

δ - U n i f o r m

FSP ^[13], which learns a policy that can beat older versions of itself sampled uniformly at random. The authors use a percentage threshold

δ \in [0, 1]

to select the old policies that are eligible for sampling from the policy zoo

π^{zoo}

, i.e., the opponent strategy

π^{'}

is sampled from

Ω (π^{'} | π^{zoo}, π) = U n i f o r m (δ | π^{zoo} |, | π^{zoo} |)

Significantly, the algorithm is the same as naive SP while $δ = 1$ . After every episode, the training policy is always inserted into the policy zoo $π^{zoo}$ . Thus, $π^{zoo}$ is updated with $π^{zoo} = π^{zoo} \cup π$ .

While AlphaStar does use FSP as one of its learning algorithms, Prioritized FSP is actually a modification proposed by the AlphaStar team in their subsequent paper ^[14]. The authors argue that many games are wasted against players that are defeated in almost 100% of games while using regular FSP and propose Prioritized FSP which samples policies by their expected win rate. Policies that are expected to win with higher probability against the current agent have higher priority and are sampled more frequently. The opponent sampling distribution

Ω

can be written as

Ω (π^{'} | π^{zoo}, π) = \frac{f (P (π b e a t s π^{'}))}{\sum_{Π \in π^{zoo}} f (P (π b e t a s Π))}

where f is a weighting function, e.g., $f (x) = {(1 - x)}^{p}$ . The policy zoo named league in the paper is complex.

OpenAI Five also employs a similar method, as described in ^[15]. The method consists of training with a naive self-play approach for 80% of the games and using past sampling policies for the remaining 20%. Similar to the Prioritized FSP method, OpenAI Five uses a dynamic sampling system that relies on a dynamically generated quality score q. This system samples opponent agents according to a softmax distribution, where the probability of choosing an opponent p is proportional to

e^{q}

. If OpenAI Five wins the game, q is updated with a learning rate constant

η

as follows:

q = q - \frac{η}{N p}

where N is the size of policy zoo. At every 10 iterations, the policy of the current agent will be added to the policy zoo with an initial quality score equal to the maximum quality score in the zoo.

While self-play can bring remarkable performance improvements to reinforcement learning, it performs poorly in non-transitive games because it always plays against itself. Specifically, the opponent’s policy only samples from one policy, which means the training agent only learns from a single type of opponent. This approach works well in situations where a higher-ranked player can always beat a lower-ranked player. Population-based training methods bring more robust policies.

4. Population-Play

Another population-based method for multi-agent systems is population-play (PP), which builds upon the concept of SP to involve multiple players and their past generations ^[14]^[16], as shown in Figure 3. With PP, a group of agents is developed and trained to compete not only with each other but also with agents from prior generations.

Figure 3. Overview of (naive) population-play.

To train an exceptional agent, AlphaStar ^[14] maintains three types of opponent pools: Main Agents, League Exploiters, and Main Exploiters. Main Agents are trained with a combination of 35% SP and 50% PFSP against all past players in the league, and the agent plays an additional 15% of matches against opponents who had previously been beaten but are now unbeatable, as well as past opponents who had previously exploited the weaknesses of the agent. League Exploiters are used to find a policy that league agents cannot defeat. They are trained using PFSP against agents in the league and added to the league if they defeat all agents in the league with a winning rate of more than 70%. Main Exploiters play against Main Agents to identify their weaknesses. If the current probability of winning is less than 20%, Main Exploiters employ PFSP against players created by Main Agents. Otherwise, Main Exploiters play directly against the current Main Agents.

For the Win (FTW) ^[16] is a training method designed for the game of Capture the Flag, which involves training a diverse population of different agents by having them learn from playing with each other. The training process involves sampling agents from the population to play as teammates and opponents, which is done using a stochastic matchmaking scheme that biases co-players to be of similar skill to the player. This ensures that a diverse set of teammates and opponents participate in training, and helps to promote robustness in the learned policies. A population-based training method is implemented to enhance the performance of weaker players and improve the overall ability of all players.

PP can accommodate a wide range of agents, making it also suitable for deployment in cooperative settings. However, Siu et al. ^[17] observed that in such scenarios, human players tended to favor rule-based agents over RL-based ones. This finding highlights the need to take into account human perceptions of AI when designing and developing systems intended for real-world adoption.

To address this issue, fictitious co-play (FCP) ^[18] aims to produce robust partners that can assist humans with different styles and skill levels without relying on human-generated data (i.e., zero-shot coordination with humans). FCP is a two-stage approach. In the first stage, N partner agents are trained independently in self-play to create a diverse pool of partners. In the second stage, FCP trains a best-response agent against the diverse pool to achieve robustness. Hidden-utility self-play ^[19] follows the FCP framework and uses a hidden reward function to model human bias with domain knowledge to solve the human–AI cooperation problem. A similar work for assistive robots learns a good latent representation for human policies ^[20].

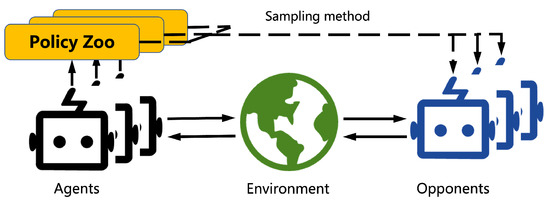
5. Evolution-Based Training Methods

Evolutionary algorithms are a family of optimization algorithms inspired by the process of natural selection. They involve generating a population of candidate solutions and iteratively improving them by applying operators such as mutation, crossover, and selection, which mimic the processes of variation, reproduction, and selection in biological evolution. These algorithms are widely used in solving complex optimization problems in various fields, including engineering, finance, and computer science. Evolutionary-based DRL is a type of PB-DRL that approaches training from an evolutionary perspective and often incorporates swarm intelligence techniques, particularly evolution algorithms.

Population-based training (PBT) introduced in ^[21] is an online evolutionary process that adapts internal rewards and hyperparameters while performing model selection by replacing underperforming agents with mutated versions of better agents. Multiple agents are trained in parallel, and they periodically exchange information by copying weights and hyperparameters. The agents evaluate their performance, and underperforming agents are replaced by mutated versions of better-performing agents. This process continues until a satisfactory performance is achieved, or a maximum budget is reached.

Majumdar et al. ^[22] propose multi-agent evolutionary reinforcement learning (MERL) as a solution for the sample inefficiency problem of PBT in cooperative MARL environments where the team reward is sparse and agent-specific reward is dense. MERL is a split-level training platform that combines both gradient-based and gradient-free optimization methods, without requiring domain-specific reward shaping. The gradient-free optimizer is used to maximize the team objective by employing an evolutionary algorithm. Specifically, the evolutionary population maintains a variety of teams and uses evolutionary algorithms to maximize team rewards (fitness). The gradient-based optimizer maximizes the local reward of each agent by using a common replay buffer with other team members in the evolutionary population. Collaborative evolutionary reinforcement learning (CERL) ^[23] is a similar work which addresses the sample inefficiency problem of PBT. It uses a collective replay buffer to share all information across the population.

Deep evolutionary reinforcement learning (DERL) ^[24] is a framework for creating embodied agents that combines evolutionary algorithms with DRL, which aims to find a diverse solutions. DERL decouples the processes of learning and evolution in a distributed asynchronous manner, using tournament-based steady-state evolution. Similar to PBT ^[21], DERL maintains a population to encourage diverse solutions. The average final reward is used as a fitness function, and a tournament-based selection method is used to choose the parents for generating children via mutation operations. Liu et al. ^[25] demonstrated that end-to-end PBT can lead to emergent cooperative behaviors in the soccer domain. They also applied an evaluation scheme based on Nash averaging to address the diversity and exploitability problem.

6. General Framework

The policy-space response oracles (PSRO) framework is currently the most widely used general framework for PB-DRL. It unifies various population-based methods, such as SP and PP, with empirical game theory to effectively solve games ^[26]. As shown in Figure 4, PSRO divides these algorithms into three modules: meta strategy, best-response solution, and policy zoo expansion. The first module, meta strategy, involves solving the meta-game using a meta-solver to obtain the meta strategy (policy distribution) of each policy zoo. The second module, best-response solution, involves each agent sampling policies of other agents

π_{- i}

and computing its best response

π_{i}

with fixed

π_{- i}

. The third module, policy zoo expansion, involves adding the best response to the corresponding policy zoo. The process starts with a single policy. In each episode, one player trains its policy

π_{i}

using a fixed policy set, which is sampled from the meta-strategies of its opponents (

π_{- i}^{'} \sim π_{- i}^{zoo}

). At the end of every epoch, each policy zoo expands by adding the approximate best response to the meta-strategy of the other players, and the expected utilities for new policy combinations computed via simulation are added to the payoff matrix.

Figure 4. Overview of PSRO.

Although PSRO has demonstrated its performance, several drawbacks have been identified and addressed by recent research. One such extension is Rectified Nash response (PSRO

_{r N}

) ^[27], which addresses the diversity issue and introduces adaptive sequences of objectives that facilitate open-ended learning. The effective diversity of the population is defined as:

d (π^{zoo}) = \sum_{i, j = 1}^{n} {⌊ ϕ (w_{i}, w_{j}) ⌋}_{+} \cdot p_{i} \cdot p_{j}

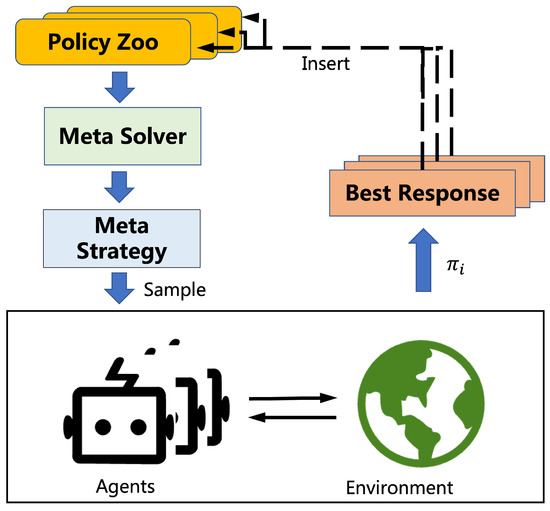
where $n = | π^{zoo} |$ , $ϕ (x, y)$ is the payoff function, $p$ is the Nash equilibrium on $π_{zoo}$ , ${⌊ x ⌋}_{+}$ is the rectifier, denoted by ${⌊ x ⌋}_{+} = x$ if $x \leq 0$ and ${⌊ x ⌋}_{+} = 0$ otherwise. Equation (7) encourages agents to play against opponents who they can beat. Perhaps surprisingly, the authors found that building objectives around the weaknesses of agents does not actually encourage diverse skills. To elaborate, when the weaknesses of an agent are emphasized during training, the gradients that guide its policy updates will be biased towards improving those weaknesses, potentially leading to overfitting to a narrow subset of the state space. This can result in a lack of diversity in the learned policies and a failure to generalize to novel situations. Several other works have also focused on the diversity aspect of PSRO frameworks. In ^[28], the authors propose a geometric interpretation of behavioral diversity in games (Diverse PSRO) and introduce a novel diversity metric that uses determinantal point process (DPP). The diversity metric is based on the expected cardinality of random samples from a DPP in which the ground set is the strategy population. It is denoted as:

D i v e r s i t y (π^{zoo}) = E_{π^{'} \sim P_{L_{π^{zoo}}}} [| π^{'} |] = T r (I - {(L_{π^{zoo}} + I)}^{- 1}),

where a DPP defines a probability $P$ , $π^{'}$ is a random subset drawn from the DPP, and $L_{π^{zoo}}$ is the DPP kernel. They incorporate this diversity metric into best-response dynamics to improve overall diversity. Similarly, ^[29] notes the absence of widely accepted definitions for diversity and offers a redefined behavioral diversity measure. The authors propose response diversity as another way to characterize diversity through the response of policies when facing different opponents.

Pipeline PSRO ^[30] is a scalable method that aims to improve the efficiency of PSRO, which is a common problem of most of PSRO-related frameworks, in finding approximate Nash equilibrium. It achieves this by maintaining a hierarchical pipeline of reinforcement learning workers, allowing it to parallelize PSRO while ensuring convergence. The method includes two classes of policies: fixed and active. Active policies are trained in a hierarchical pipeline, while fixed policies are not trained further. When the performance improvement of the lowest-level active worker in the pipeline does not meet a given threshold within a certain time period, the policy becomes fixed, and a new active policy is added to the pipeline. Another work has improved the computation efficiency and exploration efficiency by introducing a new subroutine of no-regret optimization ^[31].

PSRO framework has another branch which optimizes the meta-solver concept. Alpha-PSRO ^[32] extends the original PSRO paper to apply readily to general-sum, many-player settings, using an

α

-Rank ^[33], a ranking method that considers all pairwise comparisons between policies, as the meta-solver. Alpha-PSRO defines preference-based best response (PBR), an oracle that finds policies that maximize their rank against the population. Alpha-PSRO works by expanding the strategy pool through constructing a meta-game and calculating a payoff matrix. The meta-game is then solved to obtain a meta-strategy, and finally, a best response is calculated to find an approximate optimal response. Joint PSRO ^[34] uses correlated equilibrium as the meta-solver, and Mean-Field PSRO ^[35] proposes newly defined mean-field no-adversarial-regret learners as the meta-solver.

References

Al, S. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229.
Hernandez, D.; Denamganai, K.; Devlin, S.; Samothrakis, S.; Walker, J.A. A comparison of self-play algorithms under a generalized framework. IEEE Trans. Games 2021, 14, 221–231.
Tesauro, G. TD-Gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 1994, 6, 215–219.
Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489.
Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359.
Ye, D.; Chen, G.; Zhao, P.; Qiu, F.; Yuan, B.; Zhang, W.; Chen, S.; Sun, M.; Li, X.; Li, S.; et al. Supervised learning achieves human-level performance in moba games: A case study of honor of kings. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 908–918.
Baker, B.; Kanitscheider, I.; Markov, T.; Wu, Y.; Powell, G.; McGrew, B.; Mordatch, I. Emergent Tool Use From Multi-Agent Autocurricula. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020.
Brown, G.W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 1951, 13, 374.
Heinrich, J.; Lanctot, M.; Silver, D. Fictitious self-play in extensive-form games. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2015; pp. 805–813.
Heinrich, J.; Silver, D. Deep reinforcement learning from self-play in imperfect-information games. arXiv 2016, arXiv:1603.01121.
Shamma, J.S.; Arslan, G. Dynamic fictitious play, dynamic gradient play, and distributed convergence to Nash equilibria. IEEE Trans. Autom. Control 2005, 50, 312–327.
Lockhart, E.; Lanctot, M.; Pérolat, J.; Lespiau, J.; Morrill, D.; Timbers, F.; Tuyls, K. Computing Approximate Equilibria in Sequential Adversarial Games by Exploitability Descent. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; Kraus, S., Ed.; pp. 464–470.
Bansal, T.; Pachocki, J.; Sidor, S.; Sutskever, I.; Mordatch, I. Emergent Complexity via Multi-Agent Competition. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018.
Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354.
Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Debiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680.
Jaderberg, M.; Czarnecki, W.M.; Dunning, I.; Marris, L.; Lever, G.; Castaneda, A.G.; Beattie, C.; Rabinowitz, N.C.; Morcos, A.S.; Ruderman, A.; et al. Human-level performance in 3D multiplayer games with population-based reinforcement learning. Science 2019, 364, 859–865.
Siu, H.C.; Peña, J.; Chen, E.; Zhou, Y.; Lopez, V.; Palko, K.; Chang, K.; Allen, R. Evaluation of Human-AI Teams for Learned and Rule-Based Agents in Hanabi. In Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 16183–16195.
Strouse, D.; McKee, K.; Botvinick, M.; Hughes, E.; Everett, R. Collaborating with humans without human data. Adv. Neural Inf. Process. Syst. 2021, 34, 14502–14515.
Yu, C.; Gao, J.; Liu, W.; Xu, B.; Tang, H.; Yang, J.; Wang, Y.; Wu, Y. Learning Zero-Shot Cooperation with Humans, Assuming Humans Are Biased. arXiv 2023, arXiv:2302.01605.
He, J.Z.Y.; Erickson, Z.; Brown, D.S.; Raghunathan, A.; Dragan, A. Learning Representations that Enable Generalization in Assistive Tasks. In Proceedings of the 6th Annual Conference on Robot Learning, Auckland, New Zealand, 14–18 December 2022.
Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population Based Training of Neural Networks. arXiv 2017, arXiv:1711.09846v2.
Majumdar, S.; Khadka, S.; Miret, S.; Mcaleer, S.; Tumer, K. Evolutionary Reinforcement Learning for Sample-Efficient Multiagent Coordination. In 37th International Conference on Machine Learning; Daumé, H., Singh, A., Eds.; PMLR: Cambridge, MA, USA, 2020; Volume 119, pp. 6651–6660.
Khadka, S.; Majumdar, S.; Nassar, T.; Dwiel, Z.; Tumer, E.; Miret, S.; Liu, Y.; Tumer, K. Collaborative Evolutionary Reinforcement Learning. In 36th International Conference on Machine Learning; Chaudhuri, K., Salakhutdinov, R., Eds.; PMLR: Cambridge, MA, USA, 2019; Volume 97, pp. 3341–3350.
Gupta, A.; Savarese, S.; Ganguli, S.; Fei-Fei, L. Embodied intelligence via learning and evolution. Nat. Commun. 2021, 12, 5721.
Liu, S.; Lever, G.; Merel, J.; Tunyasuvunakool, S.; Heess, N.; Graepel, T. Emergent Coordination Through Competition. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019.
Lanctot, M.; Zambaldi, V.F.; Gruslys, A.; Lazaridou, A.; Tuyls, K.; Pérolat, J.; Silver, D.; Graepel, T. A Unified Game-Theoretic Approach to Multiagent Reinforcement Learning. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., von Luxburg, U., Bengio, S., Wallach, H.M., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4190–4203.
Balduzzi, D.; Garnelo, M.; Bachrach, Y.; Czarnecki, W.; Perolat, J.; Jaderberg, M.; Graepel, T. Open-ended learning in symmetric zero-sum games. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2019; pp. 434–443.
Perez-Nieves, N.; Yang, Y.; Slumbers, O.; Mguni, D.H.; Wen, Y.; Wang, J. Modelling behavioural diversity for learning in open-ended games. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2021; pp. 8514–8524.
Liu, X.; Jia, H.; Wen, Y.; Hu, Y.; Chen, Y.; Fan, C.; Hu, Z.; Yang, Y. Towards unifying behavioral and response diversity for open-ended learning in zero-sum games. Adv. Neural Inf. Process. Syst. 2021, 34, 941–952.
McAleer, S.; Lanier, J.B.; Fox, R.; Baldi, P. Pipeline psro: A scalable approach for finding approximate nash equilibria in large games. Adv. Neural Inf. Process. Syst. 2020, 33, 20238–20248.
Zhou, M.; Chen, J.; Wen, Y.; Zhang, W.; Yang, Y.; Yu, Y. Efficient Policy Space Response Oracles. arXiv 2022, arXiv:2202.0063v4.
Muller, P.; Omidshafiei, S.; Rowland, M.; Tuyls, K.; Perolat, J.; Liu, S.; Hennes, D.; Marris, L.; Lanctot, M.; Hughes, E.; et al. A Generalized Training Approach for Multiagent Learning. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020.
Omidshafiei, S.; Papadimitriou, C.; Piliouras, G.; Tuyls, K.; Rowland, M.; Lespiau, J.B.; Czarnecki, W.M.; Lanctot, M.; Perolat, J.; Munos, R. α-rank: Multi-agent evaluation by evolution. Sci. Rep. 2019, 9, 9937.
Marris, L.; Muller, P.; Lanctot, M.; Tuyls, K.; Graepel, T. Multi-agent training beyond zero-sum with correlated equilibrium meta-solvers. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2021; pp. 7480–7491.
Muller, P.; Rowland, M.; Elie, R.; Piliouras, G.; Pérolat, J.; Laurière, M.; Marinier, R.; Pietquin, O.; Tuyls, K. Learning Equilibria in Mean-Field Games: Introducing Mean-Field PSRO. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2022, Auckland, New Zealand, 9–13 May 2022; Faliszewski, P., Mascardi, V., Pelachaud, C., Taylor, M.E., Eds.; International Foundation for Autonomous Agents and Multiagent Systems (IFAAMAS), 2022; pp. 926–934.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Weifan Long

Taixian Hou

Xiaoyi Wei

Shichao Yan

Peng Zhai

Lihua Zhang

View Times: 637

Update Date: 15 Jun 2023

Table of Contents

Video Upload Options

Confirm