Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Zahir Hussain
 -- 2723 2023-05-10 19:22:04 |
2 layout
Camila Xu
 -850 word(s) 1873 2023-05-11 02:28:25 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Rabee, F.; Hussain, Z.M. Oriented Crossover in Genetic Algorithms. Encyclopedia. Available online: https://encyclopedia.pub/entry/44122 (accessed on 27 July 2024).
Rabee F, Hussain ZM. Oriented Crossover in Genetic Algorithms. Encyclopedia. Available at: https://encyclopedia.pub/entry/44122. Accessed July 27, 2024.
Rabee, Furkan, Zahir M. Hussain. "Oriented Crossover in Genetic Algorithms" Encyclopedia, https://encyclopedia.pub/entry/44122 (accessed July 27, 2024).
Rabee, F., & Hussain, Z.M. (2023, May 10). Oriented Crossover in Genetic Algorithms. In Encyclopedia. https://encyclopedia.pub/entry/44122
Rabee, Furkan and Zahir M. Hussain. "Oriented Crossover in Genetic Algorithms." Encyclopedia. Web. 10 May, 2023.
Oriented Crossover in Genetic Algorithms
Edit
This entry is adapted from the peer-reviewed paper 10.3390/info14050276

A genetic algorithm is a formula for resolving optimization issues that incorporate a constraint and natural selection similar to the biological process that propels evolution.

genetic algorithm uniform crossover network protocol optimization

1. Introduction

A genetic algorithm is a formula for resolving optimization issues that incorporate a constraint and natural selection similar to the biological process that propels evolution. The recent addition of the genetic algorithm (GA) to artificial intelligence was motivated by the biological behavior of chromosomes [1]. The Darwinian evaluation principle known as “survival of the fittest” is what the evolution algorithms do [1]. Therefore, the goal of employing GA is to produce the best offspring (solution), which increases the necessity of adopting it. The GA begins with two parents and mates them to generate new offspring; this mating is termed the “crossover.” then the old population is replaced with the new one by using the crossover and mutation operators. This process continues until the convergence condition is met [2].

1.1. GA Operands

There are three operands [3] in a typical GA as follows.
  • Selection: This operand determines which chromosomes of the population are selected for reproduction. If a chromosome fits better, it is more likely to be selected for reproduction.
  • Crossover: This operator exchanges the subsequences between two chromosomes before and after a locus that is randomly chosen to create two offspring [3].
  • Mutation: This procedure involves flipping one or more randomly selected bits in the parent’s chromosomes to create an offspring from a single parent [4]. Any bit has a slight chance of mutating, like 0.001 [3]. The layout shown in Figure 1 represents the typical GA process.
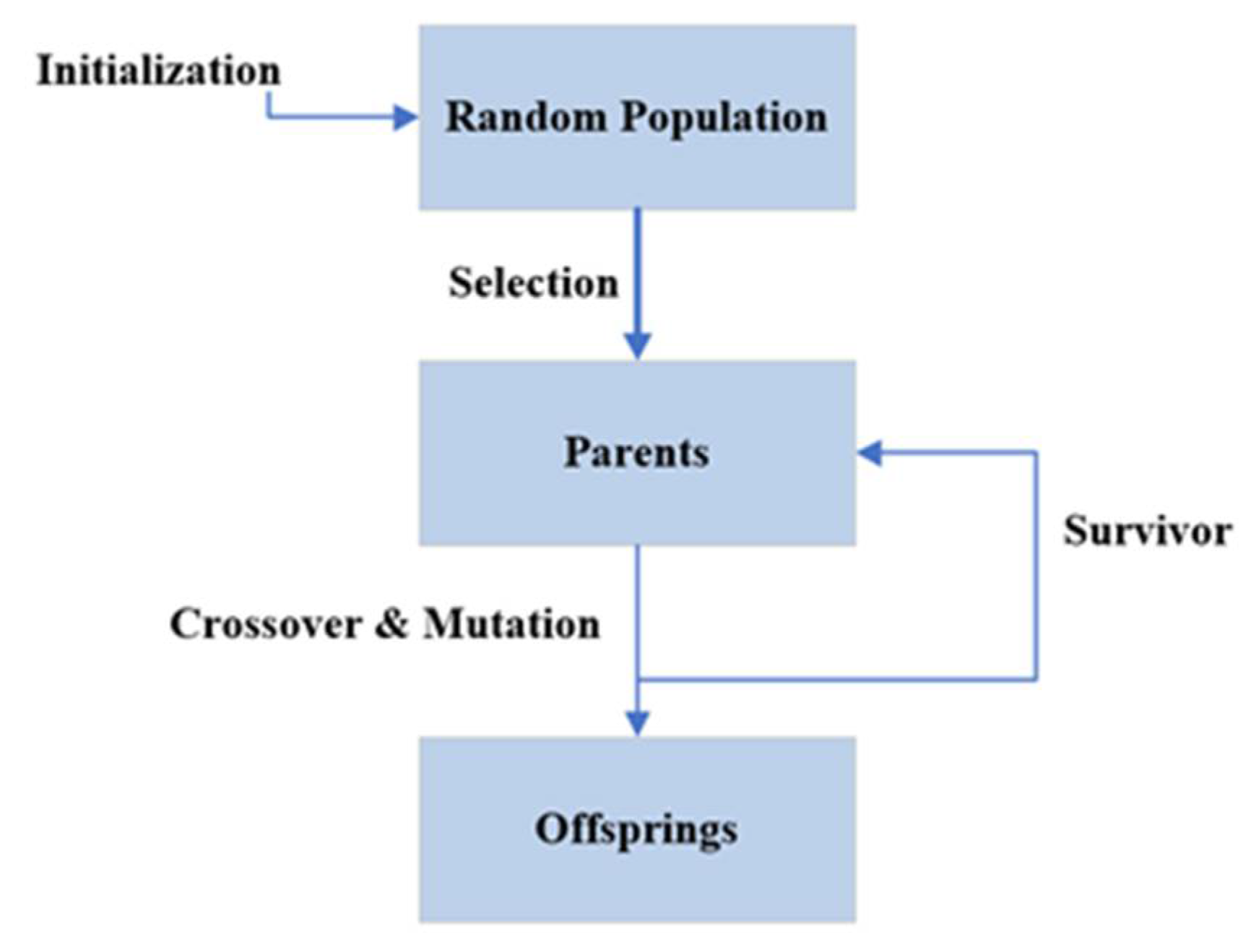
Information 14 00276 g001
Figure 1. Typical genetic algorithm design.
This approach is based on the observation that specific chromosomally encoded traits are shared by individuals and can be passed to )inherited by( their offspring through crossover [5]. The genes of either one parent or both parents, with mutations, are shared by two offspring.

1.2. Single–Point Crossover

The best-known and frequently applied crossover model so far among researchers is that presented by Ref. [6]. A crossover site is randomly selected along the length of the matched strings, and bits that are immediately near the cross-sites are exchanged.
The beneficial traits of the parents may be combined to produce better offspring when the right site is chosen. If the right place is selected when good parents are mated, the offspring will be better; if not, the string quality will be severely hampered. If the head and tail of one chromosome contain acceptable genetic material, then no offspring will acquire the two beneficial traits straight after the single-point crossover.

1.3. N-Point Crossover

Ref. [7] was the first to use the n-point crossover. It was similar to the single-point crossover. In a two-point crossover, there are two relevant crossing sites. The performance of the genetic algorithms can be severely impacted by interruptions of building blocks caused by the continual addition of the crossover sites.

1.4. Uniform Crossover

Ref. [8] presented a uniform crossover, where the chromosomes are not broken up by uniform crossover for recombination. Each gene in a child’s offspring is made by copying it from a parent who has been selected based on the bit that corresponds to it in a binary crossover mask that has the same length as the parent chromosomes. The two parents are chosen for crossover through the uniform crossover; it produces two children with n genes uniformly chosen from both parents. A random real integer determines whether the first child chooses the ith gene from the first or second parent [9].

1.5. Numerical Chromosome Representation

The crossover mostly used binary encoded chromosomes, and for real-value encoding, the numerical crossover is utilized. Here, two parent chromosomes are combined linearly by the numerical crossover operator. Two chromosomes are randomly chosen for crossover, resulting in two children who are a linear blend of their parents. N-point is mainly used in the case of binary encoded chromosomes [1].

1.6. Operators Definition

Numerous operators represent the main parts of a genetic algorithm form. A gene is a string of bits or a real number within a specific length. A chromosome is a term used to describe a sequence of genes. An allele, which can be represented by a symbol or a bit, is the smallest chromosomal unit. While a phenotype offers an external description of the individual, a genotype is a piece of data contained in a chromosome [4][10]. The main operands of GA are depicted in Figure 2.
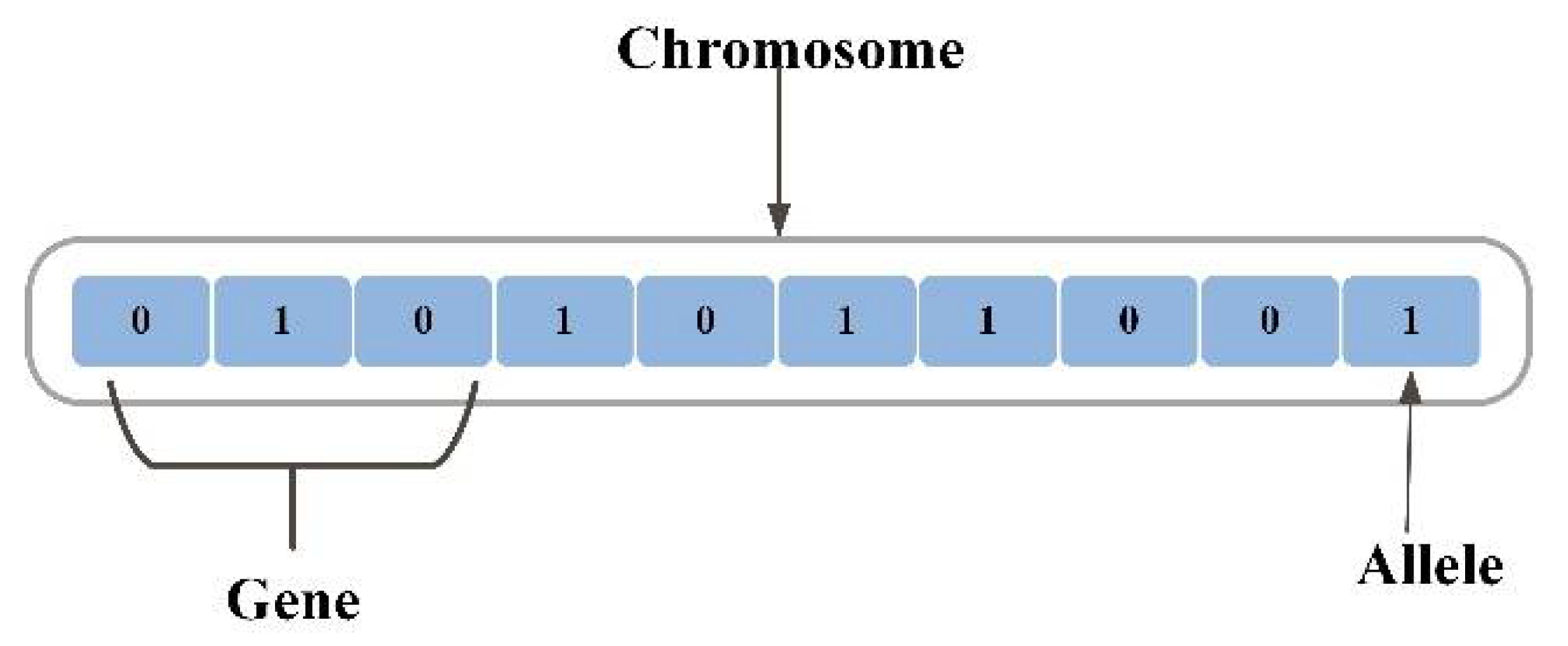
Information 14 00276 g002
Figure 2. The GA operators.

2. Genetic Algorithms for Computer Networks Optimization

2.1. Original Theories

Ref. [8] was first to present the uniform crossover for GA, even at one point, the second point was presented, but the uniform crossover showed it outperform in optimization, and till now, this crossover type is applicable in many different science fields.
Ref. [7] presented an adaptive algorithm to decide when a particular crossover (one point, second point, or uniform) will be optimal for any problem. However, it still works with the standard crossover.
Ref. [9] presented an excellent review showing more than thirty-five types of crossovers presented till 2015, and all the suggested research used in different optimization fields.
Ref. [4] presented a review that shows the importance of GA in the optimization for machine learning and deep learning.
A schema that included a two-point crossover was published in Ref. [2], where the proposed methods offer a contrastive convergence rate.
When the balance between the traits of parents and offspring was a challenge in GA optimization, Ref. [5] presented balanced crossover operators that guarantee the offspring has the same balanced features as the parents.
Ref. [4] presented a modified optimization method that depended on AI, and presented guidance for both beginner and experienced researchers designing evolutionary neural networks, assisting them in selecting appropriate genetic algorithm operator values for use in applications in a certain issue domain.

2.2. Implementation of GA

Various research works have been published on GA. The latest works will be discussed in this section.
A genetic algorithm was presented in Ref. [11] to reduce the power losses caused by turbine wakes in wind farms.
A new flight trajectory computation made with GA was proposed by Ref. [12]. The approach examined lateral and vertical navigation to determine the most fuel-efficient cruise trajectory, with optimization by GA saving up to 5.6% in gasoline.
Ref. [13] used deep learning with a convolutional neural network to classify four types of leucocytes. A genetic algorithm was used to optimize the CNN’s hyperparameters; this article showed that CNN is not efficient in getting optimal performance.
Ref. [14] presented a new optimization method called the puzzle optimization algorithm (POA), which can be used in different optimization problems. The advantage of this method is that there are no control parameters, thus not requiring parameter settings.
Ref. [15] presented a technique based on fuzzy triangular numbers that have been applied to simulate the recruitment process of the individual to the employee. Moreover, a genetic algorithm has been used for optimization, where the author presented a solution for the selection process to the best individual through a GA and fuzzy ranking.
Ref. [16] used ensemble classifiers to present a student predictive model and pre-pressing to implement a search before classifying via data-mining methodology in a context of educational data-mining (EDM). The best solution was then discovered, and GA was utilized to look for issues and raise the likelihood of reaching a solution.
Ref. [17] offered an innovative way in strong-rule generation, one of the key components of data-mining, where the author employed it differently from the existing construct rules. However, the best optimization technique for generating rules was the genetic algorithm.
Ref. [18] tried to determine the optimal choice for scheduling generator maintenance, where various multi-objective optimization methods were examined. One optimization method, non-dominated sorting genetic algorithm, exemplifies the importance of utilizing GA and optimization in a variety of scientific fields.
Ref. [19] presented a new crossover operand for the genetic algorithm called quarterly crossover (QA), by assuming a different structure for genes within the chromosome, which resulted in two crossovers intended to be an optimized solution for real-time scheduling. This reference presented expanded optimization tools and parameters for the network.
Ref. [20] presented an optimization method for an ad hoc network to be used for roadside units (RSUs) with the expectation that the proposed optimization would reduce accidents and traffic jams, but this method missed some factors related to GA and required more factors for optimization.
Ref. [21] presented a model for schedule risk management of IT outsourcing by using the distributed decision making (DDM) theory and the principal-agent theory as well as designing a hybrid algorithm from the genetic algorithm and simulated annealing algorithm. The designed algorithm focused on the risk management problem. This article is aimed at giving the decision-maker the scientific quantitative tool they need to manage the schedule risk of an IT outsourcing project.
Ref. [22] presented the bit masking oriented genetic algorithm (BMOGA) for context-free grammar induction. It used a Boolean-based approach divided into two stages, utilizing the advantages of crossover and mutation mask-fill operators to direct the search process from the ith generation to the (i + 1)th generation. To produce an appropriate amount of population in each generation, crossover and mutation mask-fill techniques are used. The article focused on the grammar of the context induction (as opposed to researchers' current work, which will focus on the computer network optimization).
In Ref. [23], the principal-agent theory was applied to ITO projects to reduce schedule risk. For the purpose of describing the vendor and client decision-making process, a two-level mathematical model was constructed. The size of the problem grows significantly as the number of activities and subprojects rises. The resulting optimization is a continuous-domain, NP-hard problem. A genetic algorithm (GA) is presented to solve this problem, where the GA model used strong optimization abilities for convergence, reliability, and efficiency, which is a good tool for this kind of optimization problem (as opposed to researchers' proposed crossover that can be applied for optimization in various fields, especially computer networks).
In the field of metaheuristic optimization, Ref. [24] presented a hybrid metaheuristic algorithm for a location-routing problem (LRP), tackles facility location problems and vehicle routing problems simultaneously to obtain the overall optimization. This article did not handle the GA crossover and did not use it (in contrast to researchers' proposed work, which modified the core of the GA crossover to get a novel adaptive crossover).
Ref. [25] is a recent article, where GA has been used in the smart contract of block chain technique to predict a new offspring of the animals endangered. This article presented a decentralized application (SONR DAPPs) by implementing a genetic algorithm to forecast a brand-new offspring with improved characteristics.

2.3. Optimization in Fields of Science

The field of cloud computing improvement and WSN is getting a lot of attention among other fields, where the energy consumption of nodes in the network should be restricted. Therefore, Ref. [26] used an optimization technique to reduce the utilization of the energy by the data center in a way to accomplish the best quality of service.
Refs. [27][28][29] presented an energy-efficient deployment method for sensor nodes by clustering the nodes and applying an optimization technique for the optimal reduction of the nodes’ battery. The optimization for nodes led to the optimization of the routing protocol. Ref. [30] used a GA for mechanical engineering in multi-scale surface roughness, and presented three genetic algorithms to superimpose and merge the mathematical descriptions of chromosomes to determine the best roughness features.‏

References

  1. Kora, P.; Yadlapalli, P. Crossover operators in genetic algorithms: A review. Int. J. Comput. Appl. 2017, 162, 34–36.
  2. Hussain, A.; Muhammad, Y.S.; Sajid, M.N. An Efficient Genetic Algorithm for Numerical Function Optimization with Two New Crossover Operators. Int. J. Math. Sci. Comput. 2018, 4, 41–55.
  3. Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998.
  4. Chiroma, H.; Abdulkareem, S.; Abubakar, A.; Herawan, T. Neural networks optimization through genetic algorithm searches: A review. Appl. Math. Inf. Sci. 2017, 11, 1543–1564.
  5. Manzoni, L.; Mariot, L.; Tuba, E. Balanced crossover operators in genetic algorithms. Swarm Evol. Comput. 2020, 54, 100646.
  6. Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975.
  7. Spears, W. Adapting Crossover in a Genetic Algorithm; Technical Report; Naval Research Laboratory: Washington, DC, USA, 1994.
  8. Syswerda, G. Uniform Crossover in Genetic Algorithms. In Proceedings of the 3rd International Conference on Genetic Algorithms, Fairfax, VA, USA, 2–9 June 1989; Morgan Kaufmann Publishers Inc., 340 Pine Street: San Francisco, CA, USA, 1989.
  9. Umbarkar, A.J.; Sheth, P.D. Crossover operators in genetic algorithms: A review. ICTACT J. Soft Comput. 2015, 6, 1083–1092.
  10. Sivanandam, S.; Deepa, S. Genetic Algorithms. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–37.
  11. Kirchner-Bossi, N.; Porté-Agel, F. Realistic wind farm layout optimization through genetic algorithms using a Gaussian wake model. Energies 2018, 11, 3268.
  12. Félix Patrón, R.S.; Botez, R.M. Flight trajectory optimization through genetic algorithms coupling vertical and lateral profiles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. 46421.
  13. Bani-Hani, D.; Khan, N.; Alsultan, F.; Karanjkar, S.; Nagarur, N. Classification of leucocytes using convolutional neural network optimized through genetic algorithm. In Proceedings of the 7th Annual World Conference of the Society for Industrial and Systems Engineering, Binghamton, NY, USA, 11–12 October 2018.
  14. Zeidabadi, F.A.; Dehghani, M. Poa: Puzzle optimization algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 273–281.
  15. Anju, K.; Avanish, K. An advanced approach to the employee recruitment process through genetic algorithm. Int. J. Inf. Technol. 2021, 13, 313–319.
  16. Begum, S.; Padmannavar, S.S. Genetically Optimized Ensemble Classifiers for Multiclass Student Performance Prediction. Int. J. Intell. Eng. Syst. 2022, 15, 316–328.
  17. Haldulakar, R.; Agrawal, J. Optimization of association rule mining through genetic algorithm. Int. J. Comput. Sci. Eng. (IJCSE) 2011, 3, 1252–1259.
  18. Muthana, S.A.; Ku-Mahamud, K.R. Comparison of Multi-objective Optimization Methods for Generator Maintenance Scheduling. Methods (Multi-Object. Metaheuristics) 2022, 14, 15.
  19. Rabee, F.; Jazaery, I.; Kumar, K. Quaternary-Child Crossover for Genetic Algorithm in Real-Time Scheduling Optimization. Int. J. Intell. Eng. Syst. 2023, 16, 100–114.
  20. Abdulkadhim, F.G.; Yi, Z.; Onaizah, A.N.; Rabee, F.; Al-Muqarm AM, A. Optimizing the Roadside Unit Deployment Mechanism in VANET with Efficient Protocol to Prevent Data Loss. Wirel. Pers. Commun. 2022, 127, 815–843.
  21. Lu, F.; Bi, H.; Huang, M.; Duan, S. Simulated Annealing Genetic Algorithm Based Schedule Risk Management of IT Outsourcing Project. Math. Probl. Eng. 2017, 2017, 6916575.
  22. Pandey, H.M.; Chaudhary, A.; Mehrotra, D. Grammar induction using bit masking oriented genetic algorithm and comparative analysis. Appl. Soft Comput. 2016, 38, 453–468.
  23. Bi, H.; Lu, F.; Duan, S.; Huang, M.; Zhu, J.; Liu, M. Two-level principal–agent model for schedule risk control of IT outsourcing project based on genetic algorithm. Eng. Appl. Artif. Intell. 2020, 91, 103584.
  24. Yan, T.; Lu, F.; Wang, S.; Wang, L.; Bi, H. A hybrid metaheuristic algorithm for the multi-objective location-routing problem in the early post-disaster stage. J. Ind. Manag. Optim. 2022, 19, 4663–4691.
  25. Abdul-Sada, H.H.; Rabee, F. The Genetic Algorithm Implementation in Smart Contract for the Blockchain Technology. Al-Salam J. Eng. Technol. 2023, 2, 37–47.
  26. Singh, J. An Optimal Resource Provisioning Scheme Using QoS in Cloud Computing Based Upon the Dynamic Clustering and Self-Adaptive Hybrid Optimization Algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 148–160.
  27. Sanapala, R.K.; Duggirala, S.R. An Optimized Energy Efficient Routing for Wireless Sensor Network using Improved Spider Monkey Optimization Algorithm. Transportation 2022, 8, 9.
  28. Jubair, A.M.; Hassan, R.; Aman, A.H.; Sallehudin, H.; Al-Mekhlafi, Z.G.; Mohammed, B.A.; Alsaffar, M.S. Optimization of Clustering in Wireless Sensor Networks: Techniques and Protocols. Appl. Sci. 2021, 11, 11448.
  29. Rangappa, M.H.; Dyamanna, G.C. Energy-Efficient Routing Protocol for Hybrid Wireless Sensor Networks Using Falcon Optimization Algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 1–10.
  30. Cinat, P.; Gnecco, G.; Paggi, M. Multi-scale surface roughness optimization through genetic algorithms. Front. Mech. Eng. 2020, 6, 29.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Artificial Intelligence; Computer Science, Theory & Methods
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Furkan Rabee
,
Zahir M. Hussain
View Times: 492
Revisions: 2 times (View History)
Update Date: 11 May 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback