Quantitative Analysis of Heart Development

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Morena Raiola	--	4064	2023-04-18 09:26:22	\|
2	update references and layout	Rita Xu	Meta information modification	4064	2023-04-18 10:34:58	\|

This entry is adapted from the peer-reviewed paper 10.3390/jcdd10040145

Heart morphogenesis is a complex and dynamic process that has captivated researchers for almost a century. This process involves three main stages, during which the heart undergoes growth and folding on itself to form its common chambered shape. Advanced imaging techniques have allowed the integration of multiscale live imaging approaches with genetic labeling, enabling the quantitative analysis of cardiac morphogenesis.

heart morphogenesis scanning laser quantitative analysis

1. Introduction

1.1. Heart Morphogenesis

The heart is the first functional organ formed in mammalian embryogenesis. After the onset of gastrulation, a primitive heart is assembled and begins to pump nutrients throughout the embryo while it continues to grow. The heart’s ability to simultaneously form and function has captivated researchers for almost a century, but imaging this complex morphogenetic processes remains a challenge for the field ^[1]^[2]^[3]^[4].

Heart morphogenesis occurs following similar phases in different species ^[5]^[6]^[7]. Heart development can be grossly divided into three stages: 1. Primitive heart tube morphogenesis, 2. Looping, lengthening, and chamber formation and 3. Chamber maturation, trabeculation, and valve formation (see Figure 1). In the first stage, cardiac progenitors in the epiblast ingress through the primitive streak into the mesodermal layer and then migrate to the anterior part of the embryo and differentiate ^[8]. These progenitors, known as the first heart field (FHF), are arranged in a horseshoe-shaped primordium in the mouse and two cardiac primordia in human, avian and zebrafish embryos ^[9]^[10]^[11]^[12], eventually forming a rudimentary beating hemi-tube called the primitive heart tube. In the second stage, the second heart field (SHF) progenitors, which are placed posteromedially and immediately adjacent to the cardiac crescent in the splanchnopleura, begin to differentiate and lengthen the primitive heart tube at the arterial and venous poles ^[2]^[13]^[14]. As the beating becomes more consistent, the heart undergoes looping, extensive growth, and morphological modifications that lead to the formation of a partially septated four-chambered heart, equipped with a set of immature valves and trabeculae ^[4]^[15]. In the final stage, the subdivision of the outflow tract and the complete interventricular and atrial septation define the morphology of the mature heart ^[16].

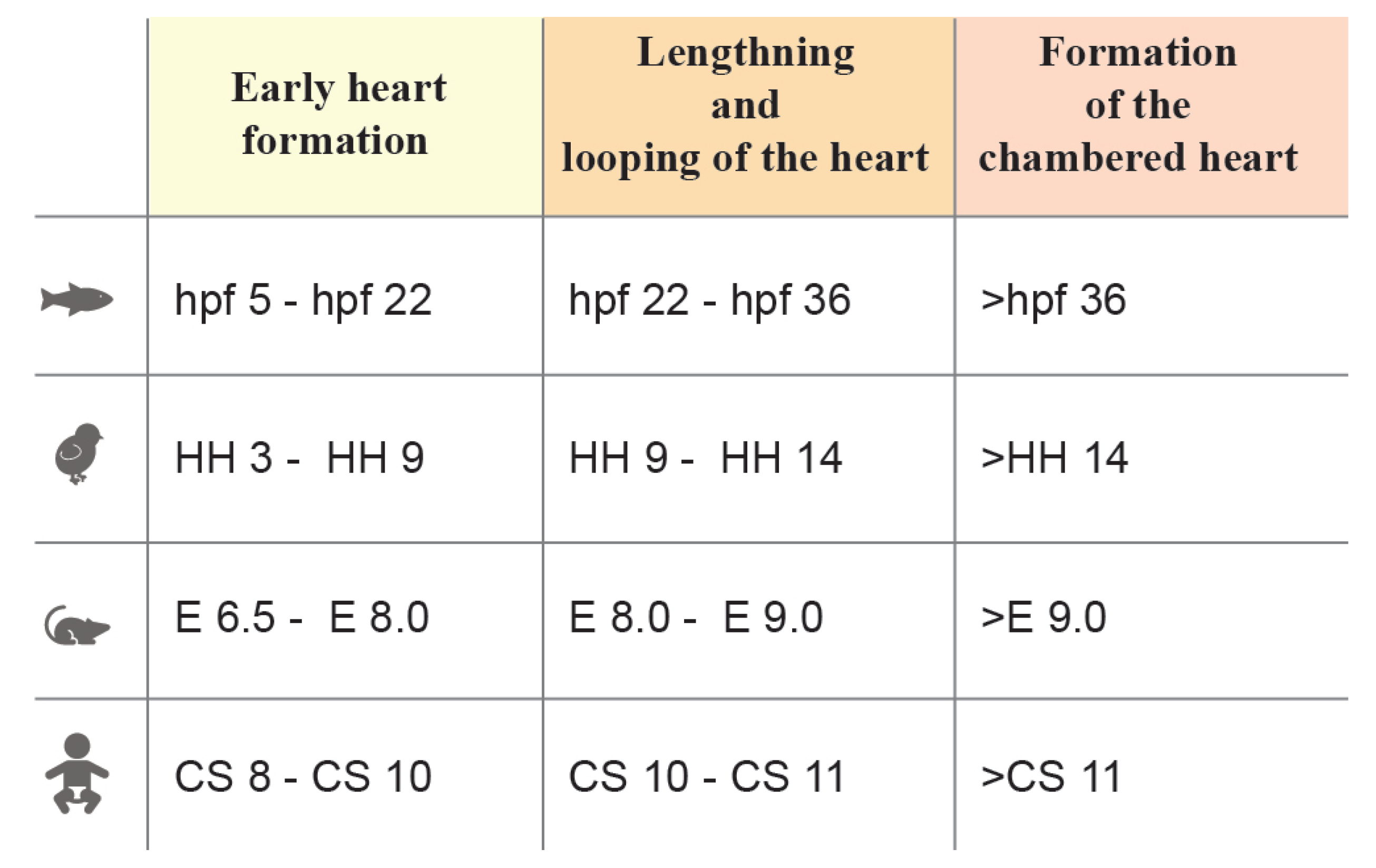
Figure 1. Stages of heart morphogenesis in vertebrate model organisms (zebrafish, chick, mouse, and human). Stage windows are reported in hours post fertilization (hpf) for zebrafish, Hamburger-Hamilton (HH) for chick embryo, embryonic day (E) for mouse embryo and Carnegie stages (CS) for human.

1.2. Quantitative Approaches towards Understanding Heart Morphogenesis

Advances in imaging technology improved our ability to study heart development ^[2]^[17]. The integration of multi-scale and live imaging approaches with genetic labeling has unlocked new insights into the molecular mechanisms shaping the heart both at the tissue and cellular levels ^[18]^[19]^[20]^[21]. These types of data required advanced image processing methods to extract relevant biological information. Over time, the field of computer graphics and machine learning has introduced powerful tools to characterize the processes that drive cardiac morphogenesis in a quantitative manner.

The three-dimensional nature of heart development makes segmentation and 3D reconstruction essential tools to interpret whole-mount images. For the simple geometries of single cells, such as nuclei or cell membranes, 3D segmentation allows one to extract geometric features which are relevant to identify the cell state. These include volume, polarity, orientation, and anisotropy, among others. Several approaches have been proposed for automated membrane/nuclear segmentation. Popular built-in models for this type of segmentation include Ilastik ^[22], Weka ^[23], Cellpose ^[24], MorphoLibJ ^[25], and StarDist ^[26], among others. More complex 3D geometries of tissues composed of multiple cell layers, such as the heart tube or trabeculae, may still require specific markers or manual steps to segment different tissue layers. Once the segmentation is reconstructed in 3D, it can be discretized in space into a polygonal mesh, creating an object that can be easily visualized, measured, and manipulated in several open-source software such as Meshlab ^[27].

2. Quantitative Approaches for Heart Morphogenesis

2.1. Static Imaging

2.1.1. Tissue-Level Analysis

When combined with clarification methods, imaging fixed samples generally offers higher resolution than imaging live embryos. Static imaging captures snapshots of tissues and cells during development, providing multiscale information to infer morphological characteristics. At the cellular level, it allows for the extraction of morphometric and morpho-mechanical features from nuclei and membrane segmentation.

When studying heart morphogenesis at the tissue level, researchers have primarily used quantitative approaches that involve extracting geometric parameters from three-dimensional (3D) reconstructions to identify key morphometric changes. One of these studies, conducted by Le Garrec et al. ^[15], explored the mechanical causes behind heart looping by measuring simple geometric parameters from 2D sections extracted from HREM 3D reconstructions. They measured heart tube elongation by measuring the length of a line passing through the centroids of all cross-sections. They also defined the timing of the breakdown of the dorsal mesocardium by measuring its change in thickness along the arterial to venous poles at different stages. Finally, they quantified the right and left angles between the heart tube and the dorsal pericardial wall, demonstrating a left-right asymmetry observable at the poles.

In a more recent study, Esteban et al. ^[19] examined 3D reconstructions of the myocardium and surrounding tissues of more than 50 specimens from cardiac crescent to heart looping (E7.75–E8.5), developed a new morphometric staging system, and registered the specimens in time and space, generating a pseudo-dynamic Atlas. The Atlas describes the average morphological evolution of the specimens and provides a map of regional morphological variability at each stage. Taking advantage of the Atlas, they computed the evolution of the angle formed by the inflow tracts and the orthogonal embryonic axes, revealing an early and progressive divergence between the angles on the left and right side (around E8.0), which constitutes the first left-right asymmetry described in the heart. Furthermore, they found that this asymmetry was reversed in Nodal mutants, in which heart looping in randomized, identifying a genetic base for this asymmetry and its causal relationship to looping.

Unlike the studies mentioned above, Paun et al. ^[28] implemented an innovative framework to compare the hearts of different specimens even before extracting geometric parameters. They used alignment and parametrization techniques to quantify trabecular morphogenesis of the heart ventricle in the mouse embryo from E14.5 to E18.5. For the first time, they quantified trabeculation using 3D fractal analysis on the volume and surface area of ventricle reconstructions from HREM images. To standardize the analysis and make it independent of geometry, they parameterized the entire surface area of the ventricles on a planar domain by flattening the tissue in their longitudinal direction as a cartography. The results showed an increased complexity of myocardium tissue from the bottom to the top of the ventricle and a decrease in overall complexity with advancing gestational age. This framework offers new possibilities for examining abnormal trabeculae in cases of congenital heart disease. In this case, 3D analysis was essential, given that, indeed, two-dimensional (2D) images alone did not provide easily comparable data due to variations in the trabeculae’s geometry.

2.1.2. Cellular-Level Analysis

Analyzing the cellular level of the heart tube plays a critical role in understanding the factors behind its formation. Characteristics of cell shape, size and orientation provide insights into the magnitude, regionalization and anisotropy of tissue growth and the mechanical forces involved in heart morphogenesis. Many quantitative approaches have been implemented to analyze cardiac morphogenesis at the cellular level, involving the extraction of geometric parameters.

Le Garrec et al. ^[29] developed a method to examine tissue anisotropy at the cellular level using 3D confocal imaging of the mouse heart. They used image segmentation, statistical analysis, and clustering techniques to determine the local coordination of cell polarity and division orientation in the embryonic mouse heart. They found that there was a significant local anisotropic coordination of ventricular cardiomyocytes at early embryonic stages. As a limitation, this study did not address the 3D nature of the problem, using flat projections for the analysis and focusing on subregions of the forming ventricles and not the whole structure.

Francou et al. ^[30] also studied cell anisotropy but focused their research on the behavior of the dorsal pericardial wall (DPW) cells in the mouse embryo. This region contains cardiac progenitors of the second heart field, which would be added to elongate the heart tube in subsequent stages. They used membrane markers to perform a thorough quantitative analysis at the cellular level based on shape geometry. They used this information to estimate the mechanical forces that cells experience and deduce anisotropic tension and cell stretching during tissue morphogenesis. They observed a polarized mechanical stress acting on cells in the posterior part and that the direction of cell elongation was significantly less oriented toward the arterial pole. They also used unsupervised classification of cell shapes to define morphological cell clusters, which distribution showed biased and directional behavior, oriented towards the arterial pole.

Along these lines, but focusing on the differentiation of the first heart field precursors, Ivanovitch et al. ^[2] measured the geometric parameters of the cell shapes to assess the changes associated with cardiomyocyte differentiation. They evaluated the roundness of cells from 2D images to characterize the difference between cardiac progenitors and differentiated cardiomyocytes, revealing that the latter was rounder and had lost columnar epithelial organization. Furthermore, they identified a transit zone in which the differentiating cardiomyocytes (according to marker expression) did not show yet a round shape. This observation suggested that changes in cell morphology alone were insufficient to distinguish differentiated cardiomyocytes, and detachment from the endoderm was also required.

While the previous studies focused on localized parts of the developing heart, Ebrahimi et al. ^[31] proposed a novel quantitative method to study cell shape at the whole heart. This was achieved by developing a computational method to measure morphometric parameters at the cell level during the C-looping stage (HH10–HH11, chicken). They combined 3D confocal microscopy and micro-CT imaging techniques to create a multi-scale 3D dataset of the entire chick heart using the finite element method. They used OpenCMISS software ^[32] to fit an initial bicubic-linear tubular mesh to the specific anatomical points of the heart for each sample, aligning them in space and time using rigid registration based on anatomical landmarks. Morphometric features were extracted directly from cells by segmenting labeled myocardial cells from 3D confocal image stacks using a deep learning base model. Different cell properties such as volume, anisotropy, and orientation were quantified and mapped to the surface of the corresponding finite element geometry of the given sample. The features were compared, showing a region-based differential spatiotemporal pattern for cellular features spatially and temporally. Although limited in conclusions due to the low number of specimens analyzed, this research represents a good example of how to integrate spatial information at different scales in the context of the whole developing organ to extract local quantitative features.

Another important contribution to the incorporation of cellular parameters to whole-organ descriptions was achieved by de Boer et al. ^[33], who generated stereological atlases of several stages of the developing mouse heart and surrounding tissues. They created the first 3D atlas of the myocardium and the surrounding splanchnic mesoderm ranging from the early cardiac crescent to the prenatal four-chambered heart. To quantify proliferation, they measured the proportion of BrdU-positive cells and mapped these data on 3D structures, revealing proliferation patterns that may drive morphogenesis. Along these lines, Meilhac et al. ^[4] had previously used data from retrospective clonal analysis to describe a regionalized pattern of proliferation in the early heart tube, however, did not provide a 3D study of this feature.

2.2. Live Imaging

Live imaging provides temporal information, allowing analysis of spatiotemporal morphogenetic events at both the tissue and the cellular levels. Tissue-level analysis using live imaging can track tissue movement to reveal the kinetics and deformation of heart tissues. In vivo imaging at the cellular level allows tracking of cell migration, division, and rearrangements, following the fate of individual cells as they differentiate into specific cell types. Fluorescence-based reporters enable the monitoring of specific gene activity in real time, providing information on spatial and temporal patterns of gene expression during the development.

2.2.1. Tissue-Level Analysis

Live imaging is a powerful tool for investigating the spatial and temporal dynamics of heart development. As such, efforts have been dedicated to developing advanced tools to extract tissue-level information from live imaging data.

One of the problems in conceptualizing the results obtained from the 3D live analysis is the complexity of 3D shape evolution. In this context, Heemskerk et al. ^[34] proposed a framework called ImSAnE (Image Surface Analysis Environment) for automatically constructing an atlas of 2D maps for dynamic tissue surfaces. ImSAnE isolates a 3D folded surface and transforms it into a sequence of 2D images that are superimposed on each other like an Earth map. Heemskerk et al. applied ImSAnE to light-sheet images of the beating heart of zebrafish, showing that the framework can recreate the cartography of the 3D heart and minimize map distortions by parametrization. By mapping the heart to a plane, they were able to follow cells in a heartbeat with relative ease and with less computational infrastructure, saving time and resources.

A further important problem when analyzing heart development data is dealing with the heartbeat. Lee et al. ^[35] designed a strategy for eliminating heartbeat artifacts in zebrafish live images for studying the trabeculation process. The team revealed the relationship between trabeculation and the contractile ability of the ventricle by analyzing synchronized 4D SPIM images of the zebrafish heart. They performed the analysis in normal embryos, in mutant embryos with reduced atrial contractions, and in embryos with reduced hemodynamic force. To understand the interaction between myocardial contractility, hemodynamic shear stress, and trabecular formation, they correlated changes in ventricular strain, fractional shortening, and ejection fraction with the trabecular structure. To assess ventricular strain, they calculated changes in circumferential displacement (D). To determine D changes, they segmented the ventricular wall and generated a boundary mesh. The mesh nodes were then adjusted to follow the motion of the ventricular wall captured by SPIM. The fractional shortening was defined as the difference between the end-diastolic displacement and end-systolic displacement. Additionally, the ejection fraction was calculated by comparing the end-diastolic and end-systolic volumes of the ventricle, calculated in the 3D reconstruction with Amira software ^[36]. To evaluate the trabecular structure, they assessed the changes in the volume of the trabecular myocardial ridges. This was done by subtracting the volume of the smooth curves, which did not include the trabecular ridges, from the overall myocardial volume. Their quantitative approach revealed a close relationship between trabeculation, contractility, and shear stress. This research is therefore a nice example of accounting for heart physiology while investigating its morphogenesis in live analysis.

Regarding heart looping in the chicken embryo, Kawahira et al. ^[37] proposed a quantitative approach to map the deformation of the myocardium during C-looping. They collected 3D+t images using a two-photon microscope. To reconstruct a deformation map of the looping process, they applied a Bayesian method on 2D cell coordinates using spherical harmonic expansion. By applying solid mechanic laws, they extracted the growth rate and anisotropy deformation for the left and right sides of the heart. The growth rate was defined as the variation of the mesh area, the anisotropy as the ratio between the principal eigenvalues and the deformation direction as the eigenvector with maximum eigenvalue. Their dynamic analysis revealed that the growth rate was similar between the two sides, suggesting that differential growth does not play a significant role in C-looping. However, deformation anisotropy showed a left-right asymmetry: while the left side underwent circumferential stretching, the right side exhibited longitudinal elongation. Therefore, this research provided a nice example of how the polarity of tissue deformation contributes to heart tube morphogenesis.

2.2.2. Cellular-Level Analysis

To understand how tissue-level transformation emerges from cell behavior, information about dynamic changes in cell shape and organization is crucial. Live imaging approaches have been employed in several studies to characterize variations in cell shape, displacement, rearrangement, and migration and how these could explain cardiac tube shaping.

In the study by ^[37], authors aimed to understand the cellular basis of differential L-R tissue anisotropy. To achieve this, cells were segmented and various geometric parameters such as volume, area, orientation, and anisotropy were determined from cell shape. Cellular features were then approximated by applying them to a 3D ellipsoid and compared between the left and right sides; however, the individual cell parameters did not explain the tissue-level anisotropy. The authors then focused on cellular rearrangement. They captured 3D time-lapse images of tissue patches at single-cell resolution from the left and right sides every 10 min and tracked approximately 30 nuclei per patch. For tracking, they used a tensor decomposition method that measures cell rearrangement as the difference between two kinds of tensors: the tissue velocity gradient tensor (LT) and the cell shape strain rate tensor (LC). LT represents the deformation per unit of time of a cell population, whereas LC represents the change in cell shape. Their study revealed, for the first time, that a dynamic rearrangement of cells within the tube plays a substantial role in left-right asymmetric tissue deformation during C-looping and is a nice example of how quantitative tracking of cell rearrangement informs the causes of tissue deformation.

Using live imaging of in vitro cultured mouse embryos, Ivanovitch et al. ^[2] used a random genetic cell lineage labeling to trace tissue and cell displacement and map the differentiation schedule of first and second heart field precursors. They described sliding of the splanchnic mesoderm over the ectoderm as an essential morphogenetic movement for transforming the cardiac crescent into the heart tube and identified alternating phases of differentiation and morphogenesis during this process. This study allowed the temporal calibration of these events with an estimated speed of the splanchnic mesoderm moving towards the midline between 12 and 20

μ

h

⁻¹. They concluded that it takes approximately 5–7 h from the late cardiac crescent stage to the open HT stage for the splanchnic mesoderm to reach the midline.

Similarly, Francou et al. ^[38] used explanted mouse tissues for the live imaging of the apicobasal polarization and basal cell dynamics to characterize the properties of SHF in the dorsal pericardial wall. They analyzed the apicobasal polarization and cell morphology between E8.5 and E9.5 by determining the circularity index and measuring the length and lifetime of the filopodia located on the basal membrane of the cells. Analyzing a Tbx1 mutant, which affects SHF progenitor addition to the heart tube, they revealed increased circularity and reduced filopodial activity in those same progenitors. Their findings highlight the importance of the epithelial properties of SHF progenitor cells in promoting heart development.

While the studies above have characterized only local cell displacements or traced reduced numbers of labeled cells, describing the complexity of cellular contributions to tissue morphogenesis requires the global tracing of all individual cells in the field of interest. Towards this goal, improvements in spatial and temporal resolution of live imaging have led to the extraction of individual cell behaviors, which involves the development of sophisticated computational tools for automatically tracking cellular movement ^[39]. These tools typically involve two parts: initially, an object detection algorithm segments individual objects in each frame; then, a linking mechanism connects these objects to create tracks. Currently, state-of-the-art segmentation techniques make use of advanced machine learning and deep learning methodologies.

McDole et al. ^[40] introduced the revised version of the Bayesian cell tracking framework, known as TGMM 2.0. The algorithm achieved an accuracy rate of 99.8% when tested on 381 manually curated tracks. To improve tracking on long-term experiments, the authors combined TGMM 2.0 with statistical vector flow analysis, providing a comprehensive understanding of cell trajectories as cells moved from the primitive streak to their specific mesodermal region. They tested the framework in 4 mouse embryos and, for the first time, created a 4D atlas of the entire embryonic morphogenesis process from gastrulation to early organogenesis (E6.5–E.8.5). Although this method excels at tracking flows of groups of cells, it was not designed to track individual cell identities over long periods of time, leaving a challenge for future tracking algorithms.

2.3. Computational Modeling

Biological systems are complex structures with a hierarchy of components organized into sub-cellular, cellular, tissue, organ, and organism levels. Consequently, alterations in any of the components may influence the others. Cellular mechanisms control and regulate the forces that define the structure of the tissue, while the structure of the tissue forces the cells into a given position, affecting the signals that the cells exchange and thus conditioning their behavior. This is why understanding an organ’s development requires characterizing the various components and exploring the intricate relationships between these at different scales. Mathematical and computational modeling approaches provide the possibility of integrating all this information to test the influence of individual components.

For example, in heart development, mathematical and computational modeling have been used in parallel with experimental methods to simulate morphogenetic events such as heart looping. Some of these models establish a determined direction of the loop ^[41], while others investigated the bending process and did not address the more complex mechanism of C-looping. Shi et al. ^[42] used a computational model to assess the hypothesis that heart bending during looping is due to differential hypertrophic growth ^[43]. Simulating the bending of the heart as a continuous sheet, they noted not only differential growth but also other factors that contributed to the bending of the heart, including change in active cell shape change ^[44]^[45], cardiac jelly swelling, dorsal mesocardium tension ^[46] and myocardial contraction ^[47], as described in previous experimental studies.

Meilhac’s group ^[15] proposed a finite element model to simulate the C-looping process and test their experimental observations. They treated the heart tube as a continuous sheet of material in the form of a regular cylinder and found that C-looping involved a buckling mechanism, resulting from specific mechanical constraints and left-right asymmetries, together with heart tube elongation. In their study, they initially simulated a differential tissue expansion in the circumferential direction. The contraction of the right side caused the arterial pole to rotate to the right. Later on, differential growth at the poles in the longitudinal direction, combined with the gradual breakdown from the dorsal mesocardium, resulted in bending in opposing directions, ultimately giving rise to a helical form.

Computational modeling is a useful tool for studying relevant processes in congenital heart diseases. Desgrange et al. ^[48] used simulations to investigate left-right asymmetry in the hearts of Nodal mutant mice. They found that Nodal is not necessary for heart looping initiation but instead modulates asymmetries at the poles of the heart tube. The researchers identified four classes of anomalies characterized by reduced asymmetries at the poles in terms of variable laterality and intensity. Simulations of a 50% reduction in intensity were sufficient to reproduce the mutant shapes, as defined by the position of the ventricles. The model was further validated by predicting the orientation of the right ventricle-left ventricle axis in all classes of shapes, which showed a strong correlation with the biological values. Therefore, the model, which included randomized laterality and a reduction of asymmetries at the poles, was able to recapitulate Nodal mutant shapes. These findings demonstrate that Nodal is necessary for amplifying and coordinating left-right asymmetries at the poles of the heart tube to generate a robust helical shape.

Recently, Honda et al. ^[49]^[50] used a computational simulation based on the cell-vertex model to verify looping conditions at the cell level in an idealized heart tube model. The cell-vertex model not only introduced the shape of the tissue but also allowed the setting of individual cell properties, controlling the shape, migration, division, and intercalation of cells during the morphogenetic process. In their model, the primitive heart was approximated as a straight tube model in which individual cells were assumed to be polygons without thickness. Since tissue bending has been shown in the literature to be due to the differential proliferation of cardiomyocytes, Honda et al. performed a computer simulation assuming that the cells on the ventral side were in a state of proliferation. The simulation showed that not only differential growth but also directional growth is required for bending. In fact, the cells were set to divide along the longitudinal axis of the heart tube. Under these simulated conditions, the heart did bend. The differential and directional growth, however, did not explain how the heart obtained its helical structure.

To explain the left-right asymmetry that generates the helical shape, researchers then applied rotational and frontal displacement to the anterior region of the tube to explain the left-right asymmetry that generates the helical shape. The results indicated that the displacement of the tube causes the left-handed screw formation of the loop. An experiment was proposed at the cellular level, and the computational model suggested that the rotational deformation of the tissue influenced the behavior of individual dividing cells.

References

Meilhac, S.M.; Buckingham, M.E. The deployment of cell lineages that form the mammalian heart. Nat. Rev. Cardiol. 2018, 15, 705–724.
Ivanovitch, K.; Temiño, S.; Torres, M. Live imaging of heart tube development in mouse reveals alternating phases of cardiac differentiation and morphogenesis. eLife 2017, 6, 30668.
Kelly, R.G.; Buckingham, M.E.; Moorman, A.F. Heart fields and cardiac morphogenesis. Cold Spring Harb. Perspect. Med. 2014, 4, a015750.
Meilhac, S.M.; Esner, M.; Kerszberg, M.; Moss, J.E.; Buckingham, M.E. Oriented clonal cell growth in the developing mouse myocardium underlies cardiac morphogenesis. J. Cell Biol. 2004, 164, 97–109.
Kemmler, C.L.; Riemslagh, F.W.; Moran, H.R.; Mosimann, C. From stripes to a beating heart: Early cardiac development in zebrafish. J. Cardiovasc. Dev. Dis. 2021, 8, 17.
Sendra, M.; Domínguez, J.N.; Torres, M.; Ocaña, O.H. Dissecting the complexity of early heart progenitor cells. J. Cardiovasc. Dev. Dis. 2022, 9, 5.
Shewale, B.; Dubois, N. Of form and function: Early cardiac morphogenesis across classical and emerging model systems. Semin. Cell Dev. Biol. 2021, 118, 107–118.
Tam, P.P.; Parameswaran, M.; Kinder, S.J.; Weinberger, R.P. The allocation of epiblast cells to the embryonic heart and other mesodermal lineages: The role of ingression and tissue movement during gastrulation. Development 1997, 124, 1631–1642.
Ivanovitch, K.; Esteban, I.; Torres, M. Growth and morphogenesis during early heart development in amniotes. J. Cardiovasc. Dev. Dis. 2017, 4, 20.
Sylva, M.; den Hoff, M.J.V.; Moorman, A.F. Development of the human heart. Am. J. Med. Genet. Part A 2014, 164, 1347–1371.
Lindsey, S.E.; Butcher, J.T.; Yalcin, H.C. Mechanical regulation of cardiac development. Front. Physiol. 2014, 5, 318.
Bakkers, J. Zebrafish as a model to study cardiac development and human cardiac disease. Cardiovasc. Res. 2011, 91, 279–288.
Lescroart, F.; Chabab, S.; Lin, X.; Rulands, S.; Paulissen, C.; Rodolosse, A.; Auer, H.; Achouri, Y.; Dubois, C.; Bondue, A.; et al. Early lineage restriction in temporally distinct populations of Mesp1 progenitors during mammalian heart development. Nat. Cell Biol. 2014, 16, 829–840.
Buckingham, M.; Meilhac, S.; Zaffran, S. Building the mammalian heart from two sources of myocardial cells. Nat. Rev. Genet. 2005, 6, 826–835.
Garrec, J.F.L.; Domínguez, J.N.; Desgrange, A.; Ivanovitch, K.D.; Raphaël, E.; Bangham, J.A.; Torres, M.; Coen, E.; Mohun, T.J.; Meilhac, S.M. A predictive model of asymmetric morphogenesis from 3D reconstructions of mouse heart looping dynamics. eLife 2017, 6, e28951.
Moorman, A.F.; Christoffels, V.M. Cardiac chamber formation: Development, genes, and evolution. Physiol. Rev. 2003, 83, 1223–1267.
Yue, Y.; Zong, W.; Li, X.; Li, J.; Zhang, Y.; Wu, R.; Liu, Y.; Cui, J.; Wang, Q.; Bian, Y.; et al. Long-term, in toto live imaging of cardiomyocyte behaviour during mouse ventricle chamber formation at single-cell resolution. Nat. Cell Biol. 2020, 22, 332–340.
Dominguez, M.H.; Krup, A.L.; Muncie, J.M.; Bruneau, B.G. Graded mesoderm assembly governs cell fate and morphogenesis of the early mammalian heart. Cell 2023, 186, 479–496.e23.
Esteban, I.; Schmidt, P.; Desgrange, A.; Raiola, M.; Temiño, S.; Meilhac, S.M.; Kobbelt, L.; Torres, M. Pseudodynamic analysis of heart tube formation in the mouse reveals strong regional variability and early left–right asymmetry. Nat. Cardiovasc. Res. 2022, 1, 504–517.
Tyser, R.C.; Ibarra-Soria, X.; McDole, K.; Jayaram, S.A.; Godwin, J.; Brand, T.A.D.; Miranda, A.M.; Scialdone, A.; Keller, P.J.; Marioni, J.C.; et al. Characterization of a common progenitor pool of the epicardium and myocardium. Science 2021, 371, eabb2986.
Zhang, Q.; Carlin, D.; Zhu, F.; Cattaneo, P.; Ideker, T.; Evans, S.M.; Bloomekatz, J.; Chi, N.C. Unveiling Complexity and Multipotentiality of Early Heart Fields. Circ. Res. 2021, 129, 474–487.
Berg, S.; Kutra, D.; Kroeger, T.; Straehle, C.N.; Kausler, B.X.; Haubold, C.; Schiegg, M.; Ales, J.; Beier, T.; Rudy, M.; et al. Ilastik: Interactive Machine Learning for (Bio)Image Analysis. Nat. Methods 2019, 16, 1226–1232.
Frank, E.; Hall, M.A.; Witten, I.H. The WEKA workbench. Data Mining 2017, 553–571.
Stringer, C.; Wang, T.; Michaelos, M.; Pachitariu, M. Cellpose: A generalist algorithm for cellular segmentation. Nat. Methods 2021, 18, 100–106.
Legland, D.; Arganda-Carreras, I.; Andrey, P. MorphoLibJ: Integrated library and plugins for mathematical morphology with ImageJ. Bioinformatics 2016, 32, 3532–3534.
Weigert, M.; Schmidt, U.; Haase, R.; Sugawara, K.; Myers, G. Star-convex polyhedra for 3D object detection and segmentation in microscopy. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision, WACV 2020, Snowmass Village, CO, USA, 1–5 March 2020; pp. 3655–3662.
Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An open-source mesh processing tool. In Proceedings of the 6th Eurographics Italian Chapter Conference 2008, Salerno, Italy, 2–4 July 2008; pp. 129–136.
Paun, B.; Bijnens, B.; Cook, A.C.; Mohun, T.J.; Butakoff, C. Quantification of the detailed cardiac left ventricular trabecular morphogenesis in the mouse embryo. Med. Image Anal. 2018, 49, 89–104.
Le Garrec, J.F.; Ragni, C.V.; Pop, S.; Dufour, A.; Olivo-Marin, J.C.; Buckingham, M.E.; Meilhac, S.M. Quantitative analysis of polarity in 3D reveals local cell coordination in the embryonic mouse heart. Development 2013, 140, 395–404.
Francou, A.; Saint-Michel, E.; Mesbah, K.; Kelly, R.G. TBX1 regulates epithelial polarity and dynamic basal filopodia in the second heart field. Development 2014, 141, 4320–4331.
Ebrahimi, N.; Osanlouy, M.; Bradley, C.P.; Kubke, M.F.; Gerneke, D.A.; Hunter, P.J. A method for investigating spatiotemporal growth patterns at cell and tissue levels during C-looping in the embryonic chick heart. iScience 2022, 25, 104600.
Bradley, C.; Bowery, A.; Britten, R.; Budelmann, V.; Camara, O.; Christie, R.; Cookson, A.; Frangi, A.F.; Gamage, T.B.; Heidlauf, T.; et al. OpenCMISS: A multi-physics & multi-scale computational infrastructure for the VPH/Physiome project. Prog. Biophys. Mol. Biol. 2011, 107, 32–47.
de Boer, B.A.; van den Berg, G.; de Boer, P.A.; Moorman, A.F.; Ruijter, J.M. Growth of the developing mouse heart: An interactive qualitative and quantitative 3D atlas. Dev. Biol. 2012, 368, 203–213.
Heemskerk, I.; Streichan, S.J. Tissue cartography: Compressing bio-image data by dimensional reduction. Nat. Methods 2015, 12, 1139–1142.
Lee, J.; Fei, P.; Packard, R.R.; Kang, H.; Xu, H.; Baek, K.I.; Jen, N.; Chen, J.; Yen, H.; Kuo, C.C.; et al. 4-Dimensional light-sheet microscopy to elucidate shear stress modulation of cardiac trabeculation. J. Clin. Investig. 2016, 126, 1679–1690.
Stalling, D.; Westerhoff, M.; Hege, H.C. Amira: A highly interactive system for visual data analysis. Vis. Handb. 2005, 38, 749–767.
Kawahira, N.; Ohtsuka, D.; Kida, N.; ichi Hironaka, K.; Morishita, Y. Quantitative Analysis of 3D Tissue Deformation Reveals Key Cellular Mechanism Associated with Initial Heart Looping. Cell Rep. 2020, 30, 3889–3903.e5.
Francou, A.; De Bono, C.; Kelly, R.G. Epithelial tension in the second heart field promotes mouse heart tube elongation. Nat. Commun. 2017, 8, 14770.
Emami, N.; Sedaei, Z.; Ferdousi, R. Computerized cell tracking: Current methods, tools and challenges. Vis. Inform. 2021, 5, 1–13.
McDole, K.; Guignard, L.; Amat, F.; Berger, A.; Malandain, G.; Royer, L.A.; Turaga, S.C.; Branson, K.; Keller, P.J. In Toto Imaging and Reconstruction of Post-Implantation Mouse Development at the Single-Cell Level. Cell 2018, 175, 859–876.e33.
Ramasubramanian, A.; Latacha, K.S.; Benjamin, J.M.; Voronov, D.A.; Ravi, A.; Taber, L.A. Computational model for early cardiac looping. Ann. Biomed. Eng. 2006, 34, 1355–1369.
Shi, Y.; Yao, J.; Xu, G.; Taber, L.A. Bending of the looping heart: Differential growth revisited. J. Biomech. Eng. 2014, 136, 081002.
Stalsberg, H.; DeHaan, R.L. The precardiac areas and formation of the tubular heart in the chick embryo. Dev. Biol. 1969, 19, 128–159.
Latacha, K.S.; Rémond, M.C.; Ramasubramanian, A.; Chen, A.Y.; Elson, E.L.; Taber, L.A. Role of actin polymerization in bending of the early heart tube. Dev. Dyn. 2005, 233, 1272–1286.
Manasek, F.J.; Burnside, M.B.; Waterman, R.E. Myocardial cell shape change as a mechanism of embryonic heart looping. Dev. Biol. 1972, 29, 349–371.
Taber, L.A. Theoretical study of Beloussov’s hyper-restoration hypothesis for mechanical regulation of morphogenesis. Biomech. Model. Mechanobiol. 2008, 7, 427–441.
Itasaki, N.; Nakamura, H.; Sumida, H.; Yasuda, M. Actin bundles on the right side in the caudal part of the heart tube play a role in dextro-looping in the embryonic chick heart. Anat. Embryol. 1991, 183, 29–39.
Desgrange, A.; Garrec, J.F.L.; Bernheim, S.; Bønnelykke, T.H.; Meilhac, S.M. Transient Nodal Signaling in Left Precursors Coordinates Opposed Asymmetries Shaping the Heart Loop. Dev. Cell 2020, 55, 413–431.e6.
Honda, H. Left-handed cardiac looping by cell chirality is mediated by position-specific convergent extensions. Biophys. J. 2021, 120, 5371–5383.
Honda, H.; Abe, T.; Fujimori, T. The Chiral Looping of the Embryonic Heart Is Formed by the Combination of Three Axial Asymmetries. Biophys. J. 2020, 118, 742–752.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Developmental Biology

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Morena Raiola

Miquel Sendra

Miguel Torres

View Times: 311

Update Date: 18 Apr 2023

Table of Contents

Video Upload Options

Confirm