You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Improvement of Single-Coil Eddy Current Sensors
Edit
This entry is adapted from the peer-reviewed paper 10.3390/s23010351

Single-coil eddy current sensors (SCECS) form a separate and independent branch among the existing eddy current probes. Such sensors are often used for aviation and aerospace applications where the conditions accompanying the measuring process are harsh and even extreme. High temperatures (up to +600 °C in the compressor and over +1000 °C in the turbine of gas turbine engines), the complex shape surfaces of the monitored parts, the multidimensional movement of the power plants’ structural elements, restrictions on the probes number and their placement in the measuring zone are the main factors affecting the reliability and accuracy of the measurement results obtained by the sensors. The application of SCECS-based systems in industrial and bench conditions made it possible to identify most of these factors and determine the ways to, if not completely eliminate, then significantly reduce their impact. The effectiveness of the considered approaches and methods has been proven in laboratories and in bench tests of power plants for various purposes. At the same time, many of the proposed solutions are not limited only to SCECS-based systems and can be successfully applied in measurement systems that use other types of eddy-current probes, as well as sensors built on other physical principles.

single-coil eddy current sensor measuring system powerplant

1. SCECS: Typical Design and Principle of Operation

There currently exists many varieties of SCECS [1][2][3][4][5][6][7][8][9][10], but they all can be divided into two main groups:
  • SCECS with SE as the whole current-carrying coil (circuit);
  • SCECS with SE as a fragment of the coil (for example, a segment of a linear conductor).
Regardless of the design, the SCECS consists of three basic functional elements: SE, MT, and current leads. The ability of the sensor to operate under extreme conditions is ensured primarily by the SE’s simple design, which does not require high temperature insulation, and its mechanical and thermal strength is determined by the properties of the material used only. For example, if the SE is made of heat-resistant steel alloy, like the one used in aircraft engine building (e.g., BZh98, EI868, XH60BT [11]; Inconel 600, Inconel 625 [12]), it retains its structural strength at temperatures above 1000 °C and ensures the sensor’s efficiency under extreme conditions in the GTE gas–air path.
The SE is placed into the measurement zone by means of current leads, which are usually made by “non-inductive” technology in the form of coaxial cylinders or closely spaced metal strips. The current leads provide the MT removal from the zone with high temperatures and connect the SE of the sensor with the secondary winding of the MT in the form of a “volume coil” that is electrically connected to the MT primary winding. To minimize the sensor’s size its MT windings are placed on the core, which is made of high-frequency ferrite with high magnetic permeability. If the temperature conditions in the measurement zone are acceptable for the magnetic circuit of the MT, then it is no longer necessary to use current leads and in the extreme case, the SE can be directly connected to the MT’s secondary winding [1][13][14].
When the monitored object is at a large distance from the SE (y → ∞), there is no electromagnetic interaction between the SE and the target (mutual inductance M = 0 and iobj = 0). If the influence of eddy currents in the SE and other sensor’s elements associated with the magnetic field caused by iSE can be neglected, the current iSE is determined only by the self-inductance LSE at the beginning of the transition process. In this case, the iSE changes in time will have an exponential growing character [2] (dashed curve) and the SE’s equivalent inductance will equal its self-inductance (Ls = LSE).
As the monitored object approaches to the SE (y → 0), the eddy currents appear in the target under the action of a magnetic field created by iSE and time-varying iobj current appears in the contour that imitates the target. The current iobj(t) affects the resulting magnetic field and this leads to the changes in the shape of the current iSE(t) and its deviation from the exponential dependence (solid curve). Such deviation can be interpreted as the influence of a time-variable equivalent inductance Ls(t), whose instability in the transition mode is explained by the influence of the eddy current iobj.

2. Factors Affecting SCECS: Types and Features of the Influence

2.1. Influence of the Specifics of the Monitored Object

The first group of influence factors is the most numerous and determines the additional errors of SCECS-based measuring instruments associated both with a change in the electrophysical characteristics of the sensor’s parts due to changing environmental conditions in the measurement zone, and with a deviation of the measurement conditions from those that were at metrological certification of systems’ measuring channels. In addition, here first and foremost, it goes about temperatures, which can vary in practical applications over a wide range from −60 to +1000 °C and higher [2][13][15][16]. The changes in geometric dimensions, electrical conductivity, and magnetic permeability of the SCESC’s SE and the monitored object materials lead to a significant change in the level of the sensor’s informative parameter (equivalent inductance), unrelated to the measuring task under these conditions. It should also be noted that SCECS’s output parameter is affected not only by high temperatures in the area where its SE is placed, but also by increased temperatures in the MT location zone. Most high-temperature SCECS use thermostable ferrites with a high Curie point value in MT (e.g., Mn-Zn ferrite core 700 NM with TC = +400 °C and initial permeability µi = 700). However, if the temperature in the MT’s location zone exceeds the Curie temperature, the SCECS characteristics dramatically deteriorate.
The dynamic loads affecting the power plant components in operation mode have also a significant influence on the conversion of the measured by SCECS technical state parameters of the monitored machines and mechanisms in addition to the high temperatures in the measuring zone. As it is noted in publications [2][3][13][17][18][19] devoted to the problems of radial clearances measuring in compressor or turbine of GTE and early wear diagnostics of turbo-pump units’ (TPU) thrust bearings by monitoring the TPU shaft’s axial displacement, the centrifugal, thrust, and aerodynamic loads lead to the complex multi-dimensional movement of the monitored constructive element (blade tip, tooth of the measurement disc, etc.), in real operating conditions of the propulsion system. In this case, the displacement of the material point selected at the monitored element has a fundamental vector character and is determined by several coordinates in the Cartesian reference system OXYZ, the center of which (point O) is rigidly attached to the SCECS installation location (geometric center (g.c.) of the sensor’s SE).
The multi-dimensional movement of the monitored objects has a significant impact on the output signal of the SCECS, which integrally contains information about all coordinates of such displacement. So, with reference to the examples above, the components of the blade tips displacement along the X and Z axes (axial displacement of the shaft and bending of the blade airfoil in the axial direction and in the direction of the wheel rotation) will be the interfering factors which make it difficult to obtain information about the measured radial clearance in GTE compressor or turbine (movement in the direction of the axis Y) [2]. Similarly, the radial displacement of the tooth of the measuring disk due to elastic and thermal deformations of the disk is the factor that makes it difficult to measure the shaft’s axial displacement in the TPU thrust bearing (displacement along the X axis) [3]. 
It should be separately noted that the need to ensure a high-precision synchronization of the inductances conversion of all SCECS in the cluster with the specified location of the monitored object relative to the sensor is another influential factor related to the dynamics of the object according to the existing cluster methods of determining the multi-coordinated movements of power plants structural units with a discrete surface (blade tips of compressor or turbine impellers, gear teeth, etc.) [2][13][17][18][19][20][21][22][23]. In [24], it is noted that in many practical applications the industrial RPM sensors (e.g., DCHV-2500 [13][18], IS-445 [3]) are traditionally used for these purposes. Unfortunately, it is not always possible to arrange the required mechanical connection of the RPM sensor with the shaft, and especially to duplicate it if the parallel measurement of rotation speed and synchronization are necessary. In addition, the PRM sensors usually provide a measurement of the “average” rotation speed, which is acceptable in the steady operation mode of the power plant, but is unacceptable in variable load modes associated, for example, with sharp revolutions set or drop.
The design features of the monitored object also affect the results of the transformation of the parameters measured by SCECS. In particular, the location of adjacent power plants’ structural elements (blades of the compressor or turbine impellers, gear teeth, etc.), can be linearly commensurate with the length of the sensor’s SE. As a result, the neighboring electrically conductive parts will affect the useful changes in the SE equivalent inductance and this influence can be very significant. In addition, the complex surface shape with which the electromagnetic interaction of the SCECS’s SE occurs is also an interfering factor, and its impact not only makes it difficult to obtain reliable data but may also cast doubt on the operation capacity of previously developed methods. For example, blades with a high curvature of the surface in their end part (the cross-section by the plane perpendicular to the blade’s axis has a sharply expressed «crescent» shape, and the cross-section of the blade’s end part by a plane parallel to the blade’s axis is «U-shaped») are used in existing and prospective turbine designs. This curvature and the complex shape of the blade means that the possible mutual locations of the SCECS’s SE and the monitored blade tip cannot be entirely determined in advance before the test starts. Therefore, the measurement information can be obtained under conditions that differ from those in which the measuring system was certified.
Finally, the feature of the SCECS placement on a monitored object is a significant influence factor, too. The limited space for sensors installed on the power plant body, for example, makes it impossible to place the required number of SCECS in the cluster. Therefore, it is necessary to abandon the measuring of separate coordinate components, and this is, as already noted, the cause of additional errors.

2.2. Electromagnetic Influence on SCECS Constructive Elements

The SCECS operation on real power plants is almost always accompanied by a rather complex electromagnetic environment related to the presence of a large number of simultaneously operating radio-electronic, electrical measuring, electromechanical and other devices that generate electromagnetic oscillations in the surrounding space, as well as the presence of natural sources of electromagnetic radiation [25].
It should also be noted that the eddy currents excited by the SE current are generated not only in the monitored structural element, but also in all parts of the SCECS design, including the SE itself. Eddy currents in the sensor parts and in the monitored object affect not only the SE circuit of the SCECS, but also interact with each other in accordance with the principle of “each with each”. As a result, the volume distribution of eddy currents over the sensor changes in time, and as a result, the sensor informative parameter (equivalent inductance) also changes in time when the object is in the same position relative to the SE of the SCECS.
It is obvious that «external» and «internal» electromagnetic fields have an impact on the operation of any eddy current probe (ECP). However, as it is noted in the introduction, the self-inductance of the SCECS SE is of about a few units, tens of nH, and its changes during the electromagnetic interaction of the sensor and the monitored object are negligible (about 1–2%). Under these conditions, the electromagnetic effect on SCECS parts is critical regardless of the nature of the radiation, and special measures to ensure an acceptable SNR are required.

3. SCECS Signals Conversion with Acceptable SNR and Uninformative Parameters Suppression

The pulse power supply is used as an effective way to increase the level of the SCECS useful signal. Contrary to the traditionally applied in the ECP high-frequency harmonic power supply [26][27][28], the pulse mode allows researchers to increase the amplitude of the information signal at the MC output by increasing the voltage of the SCECS power pulse while maintaining the average power dissipated in the sensor. The thermal mode of the sensor is achieved by reducing the pulse duration [29].
The signal at the MC output also has a pulsed nature at a pulsed SCECS power supply. It greatly simplifies further switching and analog-to-digital conversion. In addition, the non-informative parameters reduction effect can be obtained in MC by choosing in a certain way the ratio between the pulse duration and the MC time constant [30] and, in particular, the active resistance suppression, which varies widely from the temperature influence in the measuring zone.
It is noted in [11] that the beginning of the transition process at the time of formation of the read pulse (t → 0) is the most attractive time point for SCECS signals transformation. As it is known, the method of the first derivative [30] (one of test transition methods) provides the minimum duration of the pulse of a power supply among the pulse techniques used for converting the parameters of the inductive and eddy current sensors.

4. Reducing the Temperature Effect on the SCECS Informative Parameter

Traditionally the SCECS-based systems for measuring and monitoring the state of complex technical objects use the circuit methods to reduce the additional temperature error of the sensors. The methods imply the elimination of the temperature impact by using additional temperature-dependent signals. In particular, the differential MC with two identical SCECS parameters in the adjacent arms is used to convert the changes in the SCECS SE equivalent inductances during their interaction with the monitored object. The first SCECS performs working functions and directly interacts with the monitored object. The second SCECS (SCECS witness) performs compensatory functions and is installed in a separate mounting hole on the object’s body. The SE of witness SCECS (SE of SCECS2, SE2) is placed in the measurement zone in such a way that the temperature conditions for it and for the SE of the working SCECS (SE of SCECS1, SE1) would be identical, but the electromagnetic interaction between SE2 and the monitored object would not occur.
There are two versions of the most frequently used differential MC which implement the first derivative method and are implied for SCECS parameters conversion. The first MC contains the Blumlein transformer measuring bridge [31] whose two adjacent arms include SCECS1 and SCECS2 with sensing elements SE1, SE2, and matching transformers MT1, and MT2. The sensors are powered by short rectangular voltage pulses with a frequency of up to several megahertz from a switching power supply (SPS). The feed pulses are formed by the contactless key elements in the DC voltage source. The key elements and the DC voltage source are shunted by the resistors through which the energy stored in the differential circuit is dissipated during the time of the feed pulse. Magnetically coupled inductors (the coupling coefficient is equal to one) are used as a current differentiation device (DD). In this case, the DD’s input resistance is determined only by the active resistance of the inductance coils. It is shown in [13] that when the monitored object moves relative to the SE only of a single SCECS, as it just happens in the case under consideration, the voltage at the MC output at the time moment t → 0 is determined by the expression:
where L0 is the self-inductance of the SCECS (to simplify it is assumed that SCECS1 and SCECS2 are completely similar in their parameters and therefore Ls1 = Ls2 = L0); ΔL is the change in the SCECS inductances caused by the movement of the target in the sensitivity zone of the working sensor. So, the Blumlein bridge provides an almost linear conversion, and the instability of the inductance L does not have a significant impact on the result [32].
The second variant of the MC uses the operational amplifier (op-amp) as a differentiating device instead of inductance coils with close magnetic coupling [13][18][33]. The circuit contains a non-equilibrium bridge with MT of both SCECS (MT1 of SCECS1 and MT2 of SCECS2) in its adjacent arms and the current-to-voltage converters (CVC) on the base of op-amps with resistors R in the feedback circuits. The SPS is included in the bridge’s power supply diagonal and forms a brief pulsed voltage like in the previous MC variant. The CVC convert the currents into voltages at their outputs [34]. At the same time, the CVC allows the maintenance of the currents in SCECS and the time constants of the MC like in the Blumlein bridge with a similar power supply. That is why in [35] this MC was named the «electronic analog of the Blumlein bridge». The different voltage from the CVC outputs is either differentiated by the op-amp [36] or the so-called operation of “approximate differentiation” is carried out. In the last case, the difference voltage is fixed after a short time interval equal to the duration of the feed pulse and then the analog-to-digital conversion with preamplification or without it is produced [37][38]. In the last case, DD is not used and the output voltages are delivered directly to the differential inputs of the analog-to-digital converter (ADC). This ensures that the digital code at the ADC output will be proportional to the voltage difference ΔU at the end of the pulse of the power supply.
It should be noted that the use of the microelectronic base creates a perspective for the MC’s miniaturization and its integration in the SCECS or embedding into the communication line at a short distance from the sensor. Moreover, the integration of MC with ADC and microcontroller-based computing devices within a single design allows people to create so-called “intelligent sensors” [39][40] with automatically performed self-control and advanced information processing.
Unfortunately, the differential MC makes it possible to reduce the temperature effect on the sensor, but not to remove it. The main reason why the complete elimination of the temperature effect is not feasible is the technological impossibility to manufacture two absolutely identical SCECS. In addition, in most practical applications when the monitored object moves relative to the SE of only one sensor (e.g., measuring of the radial clearances in GTE), the result of the electromagnetic interaction between the SE of the working SCECS and the monitored object (blade tip) depends not only on the temperature of the sensor’s elements, but also on the temperature (more precisely, temperature changes in electrophysical parameters) of the target [41].
To further reduce the temperature effect on the SCECS the active temperature compensation methods are used. The methods involve the direct temperature measuring in the SE location zone with further algorithmic correcting of the temperature effect on the SCECS and the monitored object [13]. For this purpose, the SCECS is completed with at least one thermocouple and a hot junction is placed next to the sensor’s SE and provides the temperature measurement in the working area [2][13]. In fact, the algorithmic temperature correction involves the experimental obtaining of the calibration characteristics of the measuring channels with SCECS in the form of dependences of voltages at the MC output (more often codes after analog-to-digital conversion of the MC output signals) on the measured parameters, considering the temperature changes θ in the SE locating area. Such studies are carried out using special calibration devices with a thermal chamber and a fragment of the target just before the sensors are installed on the monitored object or test bench [13].
It is obvious that the experimental obtaining of the calibration characteristics is associated with a high complexity of the process, even with its automation [42]. The high labor intensity of the metrological experiments can be reduced by minimizing the number of points (increasing the step between the adjacent samples) at which the calibration characteristic is measured. Considering the fundamentally non-linear nature of the dependence of the equivalent inductance of the SCECS (and, accordingly, the MC output signal) on the measured parameter, the possibilities of this method of reducing the labor intensity of the calibration are limited by potentially large errors in defining the measured parameters. The alternative approach is proposed in [43][44]. It assumes the rejection from the experimental acquisition of the families of calibration characteristics and their replacement by families of the conversion functions in the form of the similar dependences of voltages (codes) at the output of the MC with SCECS on the measured parameters at different temperatures. The computer models of electromagnetic interaction between the SCECS’s SE and the target considering the further conversion of the equivalent parameters of the sensor in the MC are used to calculate the conversion functions [45][46][47][48]. The value of the final temperature error of the measuring channel with SCECS in this case is determined by the adequacy of the used models of the sensor and the MC.
It should also be noted that the design and technological limitations do not allow the thermocouple to be placed directly on the SCECS’s SE. As a result of the removal of the thermocouple from the SE along the current lead axis (even for a small distance), the temperature at the thermocouple installation point will differ from the temperature of the sensor’s SE, which is often placed in the flow of the heated moving medium of the monitored object (gas–air medium in the GTE compressor or turbine, oil flow in the lubrication system of the power plant, etc.) At the steady heat fluxes, the relationship between the SE temperature and the temperature at the point of the thermocouple installation is considered during calibration. In the case of a rapidly changing temperature (e.g., variable engine operation modes) a thermal transient process will occur in the SCECS current leads and the temperature changes at the thermocouple installation point will be delayed relative to the SE temperature changes. This will cause the voltage of the MC with SCECS to change faster than the correction algorithm will “restore” it. For a more accurate determination of the SE temperature both in stationary and transient thermal modes the thermal sensor model is proposed in [49]. The model uses the results of direct temperature measurements at two points in the SCECS body. For this purpose, an additional thermocouple is installed in the sensor’s MT location area. The same literature source [49] shows that the use of a thermal model makes it possible to reduce the SCECS additional temperature error in the transient mode to 1.1%.
In addition to the SE «temperature recovery», the additional thermocouple in the SCECS body performs the MT ferrite core temperature monitoring to prevent the exceeding of the Curie point during the sensor’s operation. If it is not possible for some reason to provide an acceptable MT temperature mode, then the forced air cooling of the MT should be used. As an alternative, the construction of the SCECS with so-called «air» MT without ferrite core is proposed in [33]. The frame of the MT primary winding of such SCECS is made of high-temperature dielectric material capable of operating in extreme temperatures. At the same time, the use of «air» MT is accompanied by a loss of the sensor’s sensitivity. The compensation of the specified effect requires greater MT and sensor dimensions.

5. Specifics of the Monitored Object Design: Impact and Ways to Reduce It

The desire to increase the efficiency of modern aviation and space equipment leads to the fact that parts of complex geometric shapes are often used in product components, and the products themselves have a complex configuration. An example is the blades of high surface curvature and complex torsional shape used in the existing and prospective GTE turbines. In addition, the adjacent elements of the product structures are located often near the monitored object and are also involved in the process of electromagnetic interaction with sensors’ SE. In relation to the example under consideration, due to the small step of blades installation on the impeller of a compressor or high-pressure turbine, the SE of SCECS is affected not only by the blade in its close proximity, but also by adjacent blades. These circumstances are additional influencing factors that not only make it difficult, but in some cases preclude the SCECS application. Possible ways to reduce the influence of the factors associated with the design features of the monitored object are given below.

5.1. Consideration of the Complex Surface Shape of Monitored Objects

The main problem of complex-shaped object monitoring is the multidimensional nature of their movements in the SCECS sensitivity zone. In this case, the electromagnetic interaction of the sensor’s SE will occur with different parts of the object’s surface varying in their geometric parameters (height and width) at each new time moment. Thus, the SCECS information parameter (inductance) will vary within a wide range even if the mutual positions of the sensor and the monitored object remain unchanged.
Based on the analysis of [19][24][33][50] it can be stated that the main way to take into account the complex surface shape of the monitored object is to select the SCECS’s installation location and the orientation of its SE in such a way that the specified features of the monitored object either do not affect the result of sensor’s output parameters conversion or can be considered in the subsequent processing of sensor’s signals. The application of computer models of the electromagnetic interaction between SCECS’s SE and the object [45][46][48] is highly effective in this case. The models allow at least to narrow the search space for acceptable solutions.
The end part of the turbine blade is given in Figure 1 as an example of a complex-shaped object. The view of the blade tip from the stator side is shown in Figure 1a and its cross-sections (A-A and B-B) are presented in Figure 1b. The protrusions in the blade’s end part are U-shaped. The distance between the protrusions depends on the blade thickness and decreases from the inlet edge to the outlet edge, as well as the curvature of the blade airfoil. The conditional blade’s geometric center is located at the intersection of the diagonals of the rectangle, into which the blade is inscribed (the blade contour line corresponding to its surface from the stator view, where 1, 2, 3, 4 are the contact points of the contour line and rectangle sides).
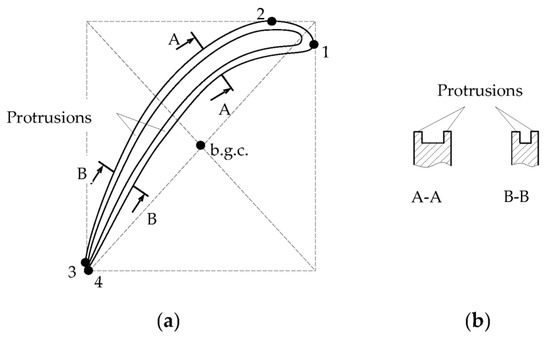
Sensors 23 00351 g007 550
Figure 1. View of the turbine blade tip from the stator side: conditional blade’s geometric center (b.g.c.) (a) and its cross-sections A-A and B-B (b).
Two methods for radial clearances measuring between the blade tips of specified shape and turbine stator under the impeller axial displacements are proposed in [33]. Both methods are implemented by the “distributed cluster” of two SCECS. The SCECS are installed on a turbine shell with the angular shift of the centers of their SE at the distance of 1.5Δψb, where Δψb is the angular pitch of the blades. The methods differ in sensor placement relative to the conventional b.g.c., as well as the orientation of their SE in relation to the blade tips. Therefore, the methods have different sensitivities to the radial clearances and permissible ranges of shaft axial displacements.
The placement of the “distributed cluster” of SCECS on the turbine stator in accordance with the first of the considered methods is shown in Figure 2a. The sensors are represented by their SE which are shifted relative to the conventional b.g.c. in such a way that the electromagnetic interaction occurs between the SE and the tip near the blade outlet edge where the curvature and the thickness are significantly less than in the middle part and, especially, near the blade inlet edge [51]. The distance between the protrusions decreases with a decrease in blade thickness and, consequently, the “protrusions effect” on the inductance changes of SE1 and SE2 is reduced. Addition reduction of the “protrusions effect” is provided by SE1 and SE2 turning by an angle of 30 ÷ 60 degrees counterclockwise relative to the direction of the impeller rotation (over z axis). As a result, the signal “doubling” at the MC output due to the specificity of the blade tips shape was avoided (the signal is shown in Figure 2b). Further extraction of the signal’s informative component is carried out in the traditional way for SCECS, which was discussed above.
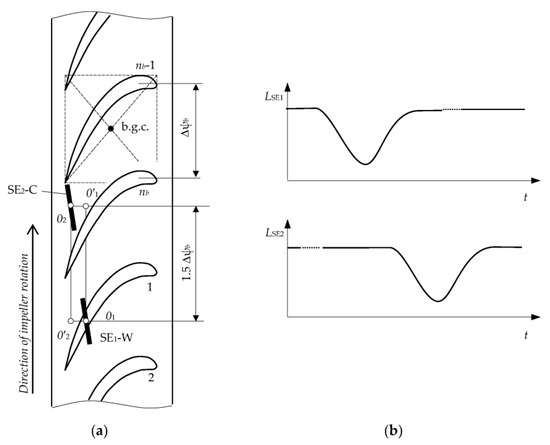
Sensors 23 00351 g008 550
Figure 2. Method 1: placement of the “distributed cluster” of SCECS on a turbine stator (a) and sensors’ SE inductance changes in time (b).
The desire to reduce the effects of blade airfoil curvature and the tips protrusions presence by the displacement of the SCECS’ SE to the outlet edge of the blade in conjunction with the SE turn (the SE are oriented almost “quasi-perpendicularly” to the contour line of the blade airfoil), leads to a significant decrease in useful changes of the SE equivalent inductances. As a result, the sensitivity to the monitored parameter (the radial clearance) is significantly low. This limits the method’s applicability, especially for high-powered engines where the changes in both clearances and shaft axial displacements can be large.
The second method [19] provides a higher sensitivity to the monitored parameters, but its implementation requires more complex processing of the MC output signals from “distributed cluster” of SCECS. In this case, SCECS are placed near the conventional b.g.c. and their SE are turned to local «quasi-parallelism» to the contour line of the blade airfoil (Figure 3a). At the same time, the effect of signal “doubling” at the MC output  (Figure 3b) manifests itself to the maximum extent when the edges of the tip’s protrusions pass through the sensitivity zones of both SCESCS. However, this effect is not eliminated in Method 2, but on the contrary, it is assumed to be useful for evaluating the shaft axial displacements.
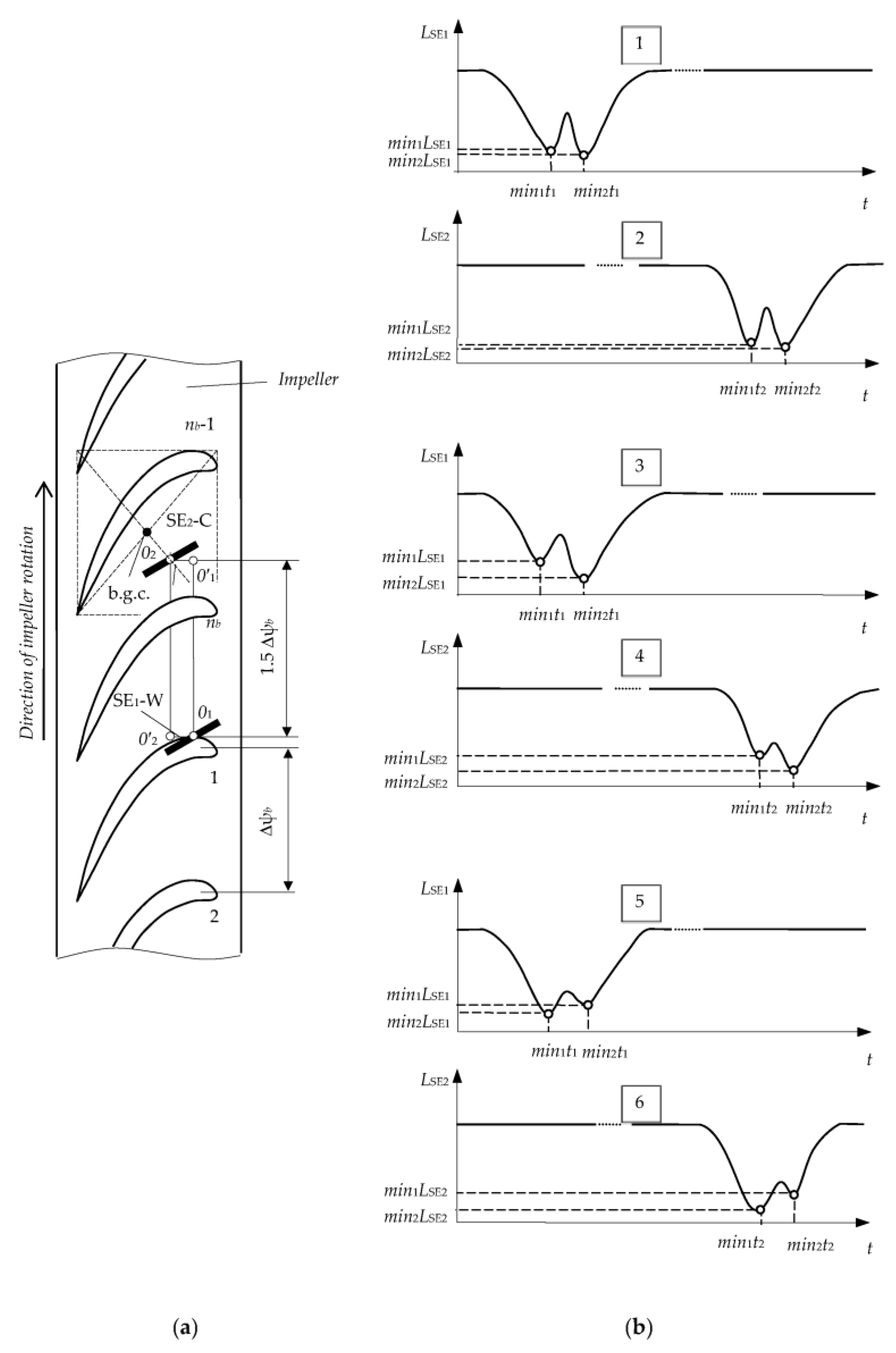
/media/item_content/202301/63be1ce7b4f71sensors-23-00351-g009.png
Figure 3. Method 2: placement of the “distributed cluster” of SCECS on a turbine stator (a) and sensors’ SE inductance changes in time (b).
For this purpose, an approximate equality of min1LSE1, min2LSE1 and min1LSE2, min2LSE2 inductances when the blade tip protrusions pass through the sensitivity zones of both SCECS (Figure 3b, diagrams 1, 2) is achieved by adjusting the turn angle of sensors’ SE. The appearance of the shaft “negative” axial displacement involves the increase in the first of two minimum values of both SE1 and SE2 inductances (min1LSE1 < min2LSE1, min1LSE2 < min2LSE2) (Figure 3b, diagrams 3, 4). Moreover, with further shaft displacement in the same direction the signal “doubling” effect gradually disappears, and the nature of both SE inductance changes becomes identical to the diagrams in Figure 2b. Similarly, the shaft axial displacement in the “positive” direction leads to the increase in the second of the two minimum values of both SE1 and SE2 inductances (Figure 3b, diagrams 5, 6) with the subsequent disappearance of the signal “doubling” effect. In other words, there is a “competition” between minimum inductance values with a “leader” change at the point x = 0 (initial position). Therefore, Method 2 considers the smallest of the two inductance minimum values as an informative parameter. If both minimums are equal, then it does not matter which one is chosen for further coordinates (radial clearances and shaft axial displacements) calculation.

5.2. Protection from the Influence of the Adjacent Elements of the Monitored Object Design on the Result of SCECS Signals Conversion

The effect associated with the influence of adjacent structural elements of the monitored object on the SCECS signals conversion has been known for a long time. In [52] it is proposed to exclude the influence of the surrounding ECP metal on the measurement result, when the sensor is installed on the monitored object, by metal removing near the sensor’s end part. With this aim, the body of the monitored object is drilled into the sensor’s location zone in such a way that a minimum gap between the ECP body and the body of the monitored object of at least 2.5 mm is ensured. Systems on the base of SCECS initially used a slightly different approach to sensors installed on the monitored object excluding the influence of the surrounding SCECS metal. For these purposes, a special fastening element for the SCECS, the holder, is used. The holder, in fact, is an element of the monitored object design and its exact copy is used on a specialized installation for calibration of the measuring channels with SCECS [11]. This ensures the identity of SCECS operating conditions during the sensor’s metrological certification and when it is installed at the monitored object.
Unfortunately, the practical applications of the measurement systems with SCECS under test bench conditions demonstrated that surrounding the SCECS metal at the place of the sensor’s installation on the body of the monitored object is not the only influencing factor of this group. In particular, the impact of adjacent blades on the results of the blade tip displacement measuring by SCECS was revealed in the tests of highly loaded stages of the GTE compressor and turbine [33][41]. Further, this effect was investigated on the basis of the models of electromagnetic interaction of the SCECS’s SE with the monitored and adjacent blades. The results of the study for the “distributed cluster” of SCECS are presented in [33][48]. For example, it is shown that reducing the pitch of the blades from 32 mm to 26 mm leads to increasing the effect of the adjacent blades by several times (up to 0.03% for the working sensor and 1.5% for the compensation sensor, i.e., the witness SCECS becomes sensitive to the movement of the monitored object and ceases to perform its compensatory functions properly). The smaller the radial gap to the monitored blade, the greater the adjacent blade’s effect.
A significant reduction of the possible errors due to the influence of adjacent blades can be achieved by replacing the existing calibration technique [33]. Unlike the well-known calibration method, the new one provides for the use of not a single, but several blades, which are installed in the calibration device on a common basis with the same pitch in a linear term as on a real object. Essentially, such a design imitates a fragment of the impeller and provides the obtaining of the families of calibration characteristics of measuring channels with SCECS considering the influence of the adjacent blades.

6. SCECS Sampling Synchronization Errors: Causes, Influence, and Ways to Reduce It

As noted earlier, the conversion of SCECS informative parameters (inductances) in many practical applications related to the position monitoring of the objects with a discrete surface (e.g., blade tips of compressor or turbine impellers, gear teeth or protrusions on measuring disks, etc.), should be performed at specified time points corresponding to strictly defined positions of the monitored object in the measurement zone. Traditionally, this problem is solved by preliminary measuring the speed of the object movement, further calculating the SCECS sampling moments, synchronizing the sampling beginning with a given object’s initial position, and, in fact, the formatting of the sensor’s pulse power supply at the calculated time points. The synchronization is usually carried out by industrial RPM sensors (e.g., DCHV-2500 [13][18], IS-445 [3]). Of course, the constant speed is assumed for all calculations.
At the same time, the production tolerances in the manufacture of individual elements of machines and mechanisms lead to the fact that, for example, blades or gear teeth may be at an unequal distance from each other and this causes the corresponding components of the measuring error. For instance, according to [53] the blade roots, which fix the blade into the turbine rotor, are made with an accuracy of ±0.01…±0.02 mm, and according to [54] the accuracy of the blade airfoil manufacturing is within ±0.03 mm. According to the estimates given in [55], the time error in SCECS power supply pulses generation during blade tips radial and axial displacement measuring can reach 6% under indicated deviations. It is proposed in [56] to correct the indicated error component by considering the individual design features of the monitored object. For these purposes, the real location of the machine elements is measured before the experiments start.
It should also be noted that the leading edge of the signal from the inductive PRM sensor changes with a change in the object speed. This results in a time shift of the entire sequence of SCECS power supply pulses. Ultimately, the error in determining the coordinates of monitored object displacements appears, although the accuracy of the period measuring remains at a high level. According to the estimates given in [55], the increase in leading edge pulse time by only 60 ns leads to the error in the SCECS channels up to 0.9%. The decrease in the edge duration of RPM signals conditioner output voltage or the application of SCECS with a modified signal converter as an RPM sensor [57] can reduce the specified error.
In addition, finally, in transient modes with fast speed changing of the monitored object moving through the SCECS measuring zone, the actual moments of the object appearing in the required position will be ahead or behind the calculated ones in which sensors’ informative parameters are fixed. As a result, the corresponding component of the measuring error appears. The error increases as the fixation moments shift from the time of synchro pulse occurrence. It is indicated in [55] regarding the task of radial and axial displacements monitoring of the compressor impeller blade tips, that the dynamic component of the error in SCECS power supply pulses generation varies from ±0.001% for the first blade up to ±17% for the 114th (last) blade under impeller speed drop from 3000 rpm to its shutdown with angular accelerations of 72 deg/s2. This effect can be significantly reduced by measuring the instantaneous velocities and accelerations of the monitored objects. In this case, there is no need to use additional RPM sensors. The required information can be obtained by special signals processing of the same SCECS that are used for the direct measurements of the coordinate displacements of the machines’ structural elements. For these purposes, the time of the extreme voltage values appear at the MC output when the adjacent elements pass through the sensitivity zone of the same SCECS is additionally fixed. The object’s speed is determined by the duration measuring of the time interval between neighboring extremes. The duration analysis of the adjacent time intervals allows for determining the object’s acceleration [58].

References

  1. Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P.; Khritin, A.A. Clearance eddy current sensors with sensitive elements the form of a segment of a conductor. Devices Control Syst. 1996, 8, 27–30.
  2. Borovik, S.; Sekisov, Y. Single-coil eddy current sensors and their application for monitoring the dangerous states of gas-turbine engines. Sensors 2020, 20, 2107.
  3. Belosludtsev, V.; Borovik, S.; Danilchenko, V.; Sekisov, Y. Wear diagnostics of the thrust bearing of NK-33 turbo-pump unit on the basis of single-coil eddy current sensors. Sensors 2021, 21, 3463.
  4. Belopukhov, V.; Blinov, A.; Borovik, S.; Luchsheva, M.; Muhutdinov, F.; Podlipnov, P.; Sazhenkov, A.; Sekisov, Y. Monitoring metal wear particles of friction pairs in the oil systems of gas turbine power plants. Energies 2022, 15, 4896.
  5. Skobelev, O.P.; Sekisov, Y.N.; Khritin, A.A. High-Temperature Conductor Eddy-Current. Converter. Patent SU No. 1394912 A1, 21 October 1986.
  6. Clarke, C.A.; Larsen, W.E. Aircraft Electromagnetic Compatibility, NASA Report No. DOT/FAA/CT-86/40. 1987. Available online: https://ntrs.nasa.gov/api/citations/19870014423/downloads/19870014423.pdf (accessed on 13 December 2022).
  7. Williams, T. EMC. In Instrumentation Reference Book, 4th ed.; Boyes, W., Ed.; Butterworth-Heinemann: Oxford, UK, 2010; pp. 797–871.
  8. Zhao, G.F.; Ying, J.; Wu, L.; Feng, Z.H. Eddy current displacement sensor with ultrahigh resolution obtained through the noise suppression of excitation voltage. Sens. Actuators A Phys. 2019, 299, 111622.
  9. Lattime, S.; Steinetz, B. Turbine Engine Clearance Control Systems: Current Practices and Future Directions. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, Indiana, 7–10 July 2022.
  10. Belopukhov, V.N.; Borovik, S.Y.; Kuteynikova, M.M.; Podlypnov, P.E.; Sekisov, Y.N.; Skobelev, O.P. The method for measuring of radial clearances in gas-turbine engine with selfcompensation of temperature effect on sensor. Sens. Syst. 2018, 4, 53–59.
  11. Zubchenko, A.S.; Koloskov, M.M.; Kashirskiy, Y.V. Steels and Alloys Grade Guide; Zubchenko, A.S., Ed.; Izd. Innovatsionnoe Mashinostroenie: Moscow, Russia, 2021; 672p.
  12. Shahwaz, M.; Nath, P.; Sen, I. A critical review on the microstructure and mechanical properties correlation of additively manufactured nickel-based superalloys. J. Alloy. Compd. 2022, 907, 164530.
  13. Sekisov, Y.N.; Skobelev, O.P.; Belenki, L.B.; Borovik, S.Y.; Raykov, B.K.; Slepnev, A.V.; Tulupova, V.V. Methods and Tools for Measuring Multidimensional Displacements of Structural Components of Power Plants; Sekisov, Y.N., Skobelev, O.P., Eds.; Izd. SamNTs RAN: Samara, Russian, 2001; 188p.
  14. Belenki, L.B.; Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P. Single-Coil Eddy Current Sensors: From Cluster Compositions to Cluster Constructions. In Proceedings of the VI International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 14–17 June 2004.
  15. Sridhar, V.; Chana, K.; Pekris, M. High Temperature Eddy Current Sensor System for Turbine Blade Tip Clearance Measurements. In Proceedings of the 12th European Conference on Turbomachinery Fluid dynamics & Thermodynamics (ETC12), Stockholm, Sweden, 3–7 April 2017.
  16. Zhao, Z.; Liu, Z.; Lyu, Y.; Gao, Y. Experimental investigation of high temperature resistant inductive sensor for blade tip clearance measurement. Sensors 2019, 19, 61.
  17. Kuteynikova, M.M. Cluster Methods and Tools for Measuring the Radial Clearances and Axial Displacements of the Blade Tips in the Turbine on the Base of Single-Coil Eddy Current Sensors. Ph.D. Thesis, Samara State Technical University, Samara, Russia, 2016.
  18. Belenki, L.B.; Borovik, S.Y.; Raykkov, B.K.; Sekisov, Y.N.; Skobelev, O.P.; Tulupova, V.V. Cluster Methods and Tools for Measuring Stator Deformations and Displacement Coordinates of Blade Tips in Gas Turbine Engines; Skobelev, O.P., Ed.; Izd. Mashinostroenie: Moscow, Russia, 2011; p. 298.
  19. Borovik, S.Y.; Kuteynikova, M.M.; Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P. Method for measuring radial and axial displacements of complex-shaped blade tips. Optoelectron. Instrum. Data Process. 2015, 51, 302–309.
  20. Borovik, S.; Sekisov, Y. Single-Coil Eddy Current Sensors. In Sensors, Measurements and Networks; Book Series: Advances in Sensors; Yurish, S.Y., Ed.; IFSA Publishing, S.L.: Barcelona, Spain, 2022; Volume 8, pp. 19–48.
  21. Borovik, S.Y.; Sekisov, Y.N.; Skobelev, O.P. Generalized representation of the methods for obtaining measurement information about the coordinates of the displacements of the blades and propellers tips. Mekhatronika Avtom. Upr. 2007, 3, 19–24.
  22. Belenki, L.B.; Borovik, S.Y.; Logvinov, A.V.; Raykov, B.K.; Sekisov, Y.N.; Skibelev, O.P.; Tulupova, V.V. Methods for measuring of blade faces displacements in compressors and turbines on basis of distributed clusters of sensors. Part 1. Measurement techniques: Reasoning and description. Mekhatronika Avtom. Upr. 2009, 4, 16–19.
  23. Borovik, S.Y.; Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P.; Tulupova, V.V. Method for Measuring the Multidimensional Displacements and Detecting the Vibrations of the Blade Tips of a Turbomachine. Rotor. Patent RF No. 2272990, 27 June 2002.
  24. Borovik, S.Y.; Kuteynikova, M.M.; Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P. Measuring of radial clearances between turbine stator and tips of blades with irregular shape by the instrumentality of single-coil eddy-current sensors. Mekhatronika Avtom. Upr. 2013, 10, 38–46.
  25. Efanov, V.I.; Tihomirov, A.A. Electromagnetic Compatibility of Radio Electronic Means and Systems; Izd. Tomsk State University: Tomsk, Russia, 2012; 228p.
  26. García-Martín, J.; Gómez-Gil, J.; Vázquez-Sánchez, E. Non-destructive techniques based on eddy current testing. Sensors 2011, 11, 2525–2565.
  27. Gerasimov, V.G.; Klyuev, V.V.; Shaternikov, V.E. Methods and Devices for Electromagnetic Control; Izd. “Spektr”: Moscow, Russian, 2010; 256p.
  28. Doebelin, E. Measurement Systems: Applications and Design, 4th ed.; McGraw-Hill Publishing Company: New York City, NY, USA, 1990; 960p.
  29. Peredelskiy, G.I. Pulse-Powered Bridge Circuits; Energoatomizdat: Moscow, Russia, 1988; 191p.
  30. Skobelev, O.P. Conversion methods based on test transients. Meas. Control Autom. 1980, 1, 11–17.
  31. Laplante, P.A. Electrical Engineering Dictionary; CRC Press LLC: Boca Raton, FL, USA, 2000; 380p.
  32. Nubert, G.P. Measuring Converters of Non-Electric Quantities. In Introduction to the Theory Calculation and Design; Fetisov, M.M., Translator; Energiya: Leningrad, Russia, 1970; 358p.
  33. Belopukhov, V.N.; Borovik, S.Y.; Kuteynikova, M.M.; Podlypnov, P.E.; Sekisov, Y.N.; Skobelev, O.P. Cluster Methods and Tools for Measuring Radial Clearances in Turbine Flow Section; Skobelev, O.P., Ed.; Izd. Innovatsionnoe Mashinostroenie: Moscow, Russia, 2018; p. 224.
  34. Carter, B.; Brown, T.R. Handbook of Operational Amplifier Applications; Texas Instruments Incorporated: Dallas, TX, USA, 2001; 94p.
  35. Belenki, L.B.; Skobelev, O.P. An electronic analogue of the measuring circuit in the form of Blumlein bridge with single-coil eddy current sensors. In Proceedings of the XIII International conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 15–17 June 2011.
  36. Peyton, A.J.; Walsh, Y. Analog Electronics with Op Amps: A Source Book of Practical Circuits; Cambridge University Press: Cambridge, UK, 1993; 293p.
  37. Belenki, L.B.; Skobelev, O.P. Measuring Circuit with Single-Coil Eddy Current Sensors and Approximate Differentiation. In Proceedings of the XIV International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 19–22 June 2012.
  38. Belenki, L.B.; Kuteynikova, M.M.; Logvinov, A.V.; Sekisov, Y.N.; Skobelev, O.P. Device for Measuring of Multi-Coordinate Displacements of the Blades’. Tips. Patent RF No. 2525614, 27 December 2012.
  39. Morris, A.S.; Langari, R. Measurement and Instrumentation: Theory and Application, 3d ed.; Academic Press: New York City, NY, USA, 2020; 736p.
  40. Finkelstein, L. Intelligent and knowledge-based instrumentation. An examination of basic concepts. Measurement 1994, 14, 23–29.
  41. Podlypnov, P.E. Temperature impact on the controlled and adjacent blades of the compressor impeller when measuring the radial clearances with self-compensation of temperature effects on the sensor. Vestn. SamGTU. Ser. Tekhnicheskie Nauk. 2018, 59, 106–117.
  42. Belopukhov, V.N.; Borovik, S.Y.; Podlypnov, P.E. Hardware and Software Tools for Automation of Experimental Investigations of the Families of Calibration Characteristics of the Systems for Measuring the Coordinates of Displacements. In Proceedings of the XVI International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 30 June–3 July 2014.
  43. Borovik, S.Y.; Kuteynikova, M.M.; Sekisov, Y.N.; Skobelev, O.P. Analysis of temperature influence on the informative parameters of single-coil eddy current sensors. Optoelectron. Instrum. Data Process. 2017, 53, 395–401.
  44. Borovik, S.Y.; Kuteynikova, M.M.; Sekisov, Y.N.; Skobelev, O.P. Influence of turbine wheelspace temperature on measurements of radial and axial displacements of blade tips. Optoelectron. Instrum. Data Process. 2018, 54, 105–111.
  45. Borovik, S.Y.; Marinina, Y.V.; Sekisov, Y.N. Model of a cluster single-coil eddy current sensor based on the finite element method. Vestn. SamGTU. Ser. Tekhnicheskie Nauk. 2007, 19, 76–83.
  46. Kuteynikova, M.M.; Sekisov, Y.N. Models of Electromagnetic Interaction of Sensitive Elements of Single-Coil Eddy Current Sensors and Blades. Status and Development. In Proceedings of the XIV International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 19–22 June 2012.
  47. Borovik, S.Y.; Kuteynikova, M.M.; Sekisov, Y.N.; Skobelev, O.P. Model of the Measuring Circuit with Variable in Time Inductances of Single-Coil Eddy Current Sensors. In Proceedings of the XVI International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 30 June–3 July 2014.
  48. Borovik, S.Y.; Kuteynikova, M.M.; Podlipnov, P.E.; Sekisov, Y.N.; Skobelev, O.P. Modeling the process of measuring radial and axial displacements of complex-shaped blade tips. Optoelectron. Instrum. Data Process. 2015, 51, 512–522.
  49. Borovik, S.Y.; Sekisov, Y.N. On the Use of a Thermal Model of a Single-Coil Eddy Current Sensor for the Correction of Temperature Errors. In Proceedings of the VII International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 27 June–1 July 2005.
  50. NDT Accessories/Zubehör. Product Catalog/Produktkatalog. Release 18b. Available online: https://www.pruftechnik.com/fileadmin/Products-Services/Products/NDT/NDT-Accessories/Encoders-Paint-markers-Warning-units-Test-defect/Downloads/PRUEFTECHNIK_NDT_Accessories_Catalog_EN-DE.pdf (accessed on 13 December 2022).
  51. Belenki, L.B.; Kuteynikova, M.M.; Raykov, B.K.; Sekisov, Y.N.; Skobelev, O.P. Method for measuring of radial clearances and axial displacements of the blades’ tips of turbine. impeller. Patent RF No. 2457432, 30 December 2010.
  52. Kaman Instrumentation. High Temperature Displacement System. User Manual. Available online: https://www.kamansensors.com/wp-content/uploads/2016/10/Kaman_High_Temperature_Sensors_manual.pdf (accessed on 23 November 2022).
  53. Development and Analysis of the Technological Process of Machining of LPT Nozzle Blades. Available online: https://www.turbinist.ru/98-razrabotka-i-analiz-tekhnologicheskogo-processa.html (accessed on 23 November 2022).
  54. Geykin, V. The perfection of the engine is determined by the perfection of the technology. Engine 2003, 3, 11–15.
  55. Borovik, S.Y.; Skobelev, O.P. Method errors of the systems for measuring of blade tips radial and axial displacements. Mekhatronika Avtom. Upr. 2012, 4, 31–35.
  56. Borovik, S.Y. On the error correction of measuring of blades tips radial and axial displacements cause to irregular blade pitch on turbomachine wheel. Vestn. SamGTU. Ser. Tekhnicheskie Nauk. 2014, 42, 25–31.
  57. Belopukhov, V.N.; Sekisov, Y.N.; Skobelev, O.P. GTE Rotor Speed Measuring System Based on Single-Coil Eddy Current Sensors. In Proceedings of the XIII International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 15–17 June 2011.
  58. Belopukhov, V.N.; Borovik, S.Y. System for Measuring the Accelerations of the Compressor and Turbine Blade Wheel Using a Single-Coil Eddy Current Sensors and a Microcontroller. In Proceedings of the XIV International Conference “Complex Systems: Control and Modelling Problems”, Samara, Russian, 19–22 June 2012.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Instruments & Instrumentation
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Sergey Borovik
,
Marina Kuteynikova
,
Yuriy Sekisov
View Times: 592
Revisions: 3 times (View History)
Update Date: 13 Jan 2023
Table of Contents
Academic Video Service
Feedback