1. Experiments with Redox Proteins

Small redox proteins such as cytochromes and ferredoxins can be investigated on condition that their electroactive coverage (the amount of protein undergoing direct electron transfer) is large enough (in practice, greater than a fraction of pmol/cm²).

Electrochemical data obtained with small proteins can be used to measure the redox potentials of the protein's redox sites,^[1] the rate of electron transfer between the protein and the electrode,^[2] or the rates of chemical reactions (such as protonations) that are coupled to electron transfer.^[3]

1.1. Interpretation of the Peak Current and Peak Area

Fig 1. Voltammetric signals for a one-electron (A) or two-electron (B) redox species adsorbed onto an electrode in the limit of slow scan rate. The current plotted here is normalized by ${\displaystyle F^2\nu A\mathrm{\Gamma }/RT}$, implying that the measured current increases in proportion to scan rate (${\displaystyle \nu }$). https://handwiki.org/wiki/index.php?curid=2069956

Fig 2. Effect of scan rate on the voltammetry of a one-electron redox species adsorbed onto an electrode (the current shown here is normalized by ${\displaystyle F^2\nu A\mathrm{\Gamma }/RT}$, implying that the measured current increases in proportion to scan rate (${\displaystyle \nu }$)) calculated for ${\displaystyle \alpha =0.5}$, ${\displaystyle T=298}$K. The scan rate increases from blue to red. A: voltammograms. B: peak potentials. https://handwiki.org/wiki/index.php?curid=2032455

In a cyclic voltammetry experiment carried out with an adsorbed redox protein, the oxidation and reduction of each redox site shows as a pair of positive and negative peaks. Since all the sample is oxidised or reduced during the potential sweep, the peak current and peak area should be proportional to scan rate (observing that the peak current is proportional to scan rate proves that the redox species that gives the peak is actually immobilised).^[1] The same is true for experiments performed with non-biological redox molecules adsorbed onto electrodes. The theory was mainly developed by the French electrochemist Etienne Laviron in the 1980s^[2],[4],.^[5]

Since both this faradaic current (which results from the oxidation/reduction of the adsorbed molecule) and the capacitive current (which results from electrode charging) increase in proportion to scan rate, the peaks should remain visible when the scan rate is increased. In contrast, when the redox analyte is in solution and diffuses to/from the electrode, the peak current is proportional to the square root of the scan rate (see: Randles–Sevcik equation).

Peak area

Irrespective of scan rate, the area under the peak (in units of AV) is equal to ${\displaystyle nFA\mathrm{\Gamma }\nu }$, where ${\displaystyle n}$ is the number of electrons exchanged in the oxidation/reduction of the center, ${\displaystyle A}$ is the electrode surface and ${\displaystyle \mathrm{\Gamma }}$ is the electroactive coverage (in units of mol/cm²).^[1] The latter can therefore be deduced from the area under the peak after subtraction of the capacitive current.

Peak shape

Slow scan rate

At slow scan rates there should be no separation between the oxidative and reductive peaks.

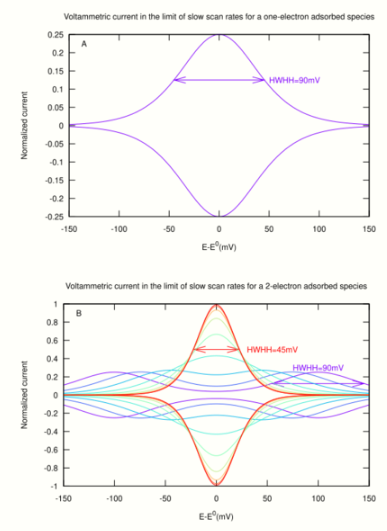
• A one-electron site (e.g. a heme or FeS cluster) gives a broad peak (fig 1A). The equation that gives the shape and intensity of the peak is:

${\displaystyle \frac{i}{F^2\nu A\mathrm{\Gamma }/RT}=\pm \frac{\exp (\frac{F}{RT}(E-E^0))}{(1+\exp {(\frac{F}{RT}(E-E^0))}^2}}$

Ideally, the peak position is ${\displaystyle E_p=E^0}$ in both directions. The peak current is ${\displaystyle i_p=F^2\nu A\mathrm{\Gamma }/4RT}$ (it is proportional to scan rate, ${\displaystyle \nu }$, and to the amount of redox sites on the electrode, ${\displaystyle A\mathrm{\Gamma }}$). The ideal half width at half height (HWHH) equates ${\displaystyle RT/F\times \ln (3+2\sqrt{2})=89}$ mV at 20 °C. Non-ideal behaviour may result in the peak being broader than the ideal limit.

• The peak shape for a two-electron redox site (e.g. a flavin) depends on the stability of the half-reduced state (fig 1B). If the half-reduced state is stable over a large range of electrode potential, the signal is the sum of two one-electron peaks (purple line in fig 1B). If the half reduced state is unstable, the signal is a single peak (red line in fig 1B), which may have up to four times the height and half the width of a one-electron peak.^[4],[6]
• A protein that contains multiple redox centers should give multiple peaks which all have the same area (scaled by ${\displaystyle n}$).

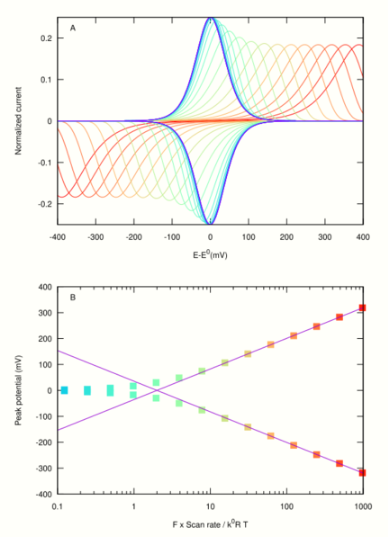
Fast scan rates

If the reaction is a simple electron transfer reaction, the peaks should remain symmetrical at fast scan rates. A peak separation is observed when the scan rate ${\displaystyle \nu \gg RT{k}^0/F}$, where ${\displaystyle k_0}$ is the exchange electron transfer rate constant in Butler Volmer theory. Laviron equation^[2],[6],[7] predicts that at fast scan rates, the peaks separate in proportion to ${\displaystyle \log (\nu /k^0)}$. The larger ${\displaystyle \nu }$ or the smaller ${\displaystyle k^0}$, the larger the peak separation. The peak potentials are ${\displaystyle E_p=E^0\pm \frac{RT}{\alpha F}\ln \frac{\alpha F\nu }{k^{0}RT}}$,^[2] as shown by lines in fig 2B (${\displaystyle \alpha }$ is the charge transfer coefficient). Examining the experimental change in peak position against scan rate therefore informs on the rate of interfacial electron transfer ${\displaystyle k^0}$.

Effect of coupled chemical reactions

Coupled reactions are reactions whose rate or equilibrium constant is not the same for the oxidized and reduced forms of the species that is being investigated. For example, reduction should favour protonation (${\displaystyle p{K}_a^{\mathrm{o}\mathrm{x}}<p{K}_a^{\mathrm{r}\mathrm{e}\mathrm{d}}}$): the protonation reaction is coupled to the reduction at ${\displaystyle p{K}_a^{\mathrm{o}\mathrm{x}}<pH<p{K}_a^{\mathrm{r}\mathrm{e}\mathrm{d}}}$. The binding of a small molecule (other than the proton) may also be coupled to a redox reaction.

Two cases must be considered depending on whether the coupled reaction is slow or fast (meaning that the time scale of the coupled reaction is larger or smaller than the voltammetric time scale^[8] ${\displaystyle \tau =RT/F\nu }$).

• Fast chemical reactions that are coupled to electron transfer (such as protonation) only affect the apparent values of ${\displaystyle E^0}$ and ${\displaystyle k^0}$,^[5] but the peaks remain symmetrical. The dependence of ${\displaystyle E^0}$ on ligand concentration (e.g. the dependence of ${\displaystyle E^0}$ on pH plotted in a Pourbaix diagram) can be interpreted to obtain the dissociation constants (e.g. acidity constants) from the oxidized or reduced forms of the redox species.
• Asymmetry may result from slow chemical reactions that are coupled to (and gate) the electron transfer. From fast scan voltammetry, information can be gained about the rates of the reactions that are coupled to electron transfer. The case of ${\displaystyle n=1}$ and ${\displaystyle n=2}$ reversible surface electrochemical reactions followed by irreversible chemical reactions was addressed by Laviron in refs^[4],[9] but the data are usually interpreted using the numerical solution of the appropriate differential equations.^[7]

2. Experiments with Redox Enzymes

In studies of enzymes, the current results from the catalytic oxydation or reduction of the enzyme's substrate.

The electroactive coverage of large redox enzymes (such as laccase, hydrogenase etc.) is often too low to detect any signal in the absence of substrate, but the electrochemical signal is amplified by catalysis: indeed, the catalytic current is proportional to turnover rate times electroactive coverage. The effect of varying the electrode potential, the pH or the concentration of substrates and inhibitors etc. can be examined to learn about various steps in the catalytic mechanism.^[6]

2.1. Interpretation of the Value of the Catalytic Current

For an enzyme immobilised on an electrode, the value of the current at a certain potential equates ${\displaystyle \pm nFA\mathrm{\Gamma }\times \mathrm{T}\mathrm{O}\mathrm{F}}$, where ${\displaystyle n}$ is the number of electrons exchanged in the catalytic reaction, ${\displaystyle A}$ is the electrode surface, ${\displaystyle \mathrm{\Gamma }}$ is the electroactive coverage, and TOF is the turnover frequency (or "turnover number"), that is, the number of substrate molecules transformed per second and per molecule of adsorbed enzyme).The latter can be deduced from the absolute value of the current only on condition that ${\displaystyle A\mathrm{\Gamma }}$ is known, which is rarely the case. However, information is obtained by analysing the relative change in current that results from changing the experimental conditions.

The factors that may influence the TOF are (i) the mass transport of substrate towards the electrode where the enzyme is immobilised (diffusion and convection), (ii) the rate of electron transfer between the electrode and the enzyme (interfacial electron transfer), and (iii) the "intrinsic" activity of the enzyme, all of which may depend on electrode potential.

The enzyme is often immobilized on a rotating disk working electrode (RDE) that is spun quickly to prevent the depletion of the substrate near the electrode. In that case, mass transport of substrate towards the electrode where the enzyme is adsorbed may not be influential.

Steady-state voltammetric response

Under very oxidising or very reducing conditions, the steady-state catalytic current sometimes tends to a limiting value (a plateau) which (still provided there is no mass transport limitation) relates to the activity of the fully oxidised or fully reduced enzyme, respectively. If interfacial electron transfer is slow and if there is a distribution of electron transfer rates (resulting from a distribution of orientations of the enzymes molecules on the electrode), the current keeps increasing linearly with potential instead of reaching a plateau; in that case the limiting slope is proportional to the turnover rate of the fully oxidised or fully reduced enzyme.^[6]

The change in steady-state current against potential is often complex (e.g. not merely sigmoidal).^[10]

Departure from steady-state

Another level of complexity comes from the existence of slow redox-driven reactions that may change the activity of the enzyme and make the response depart from steady-state.^[11] Here, slow means that the time scale of the (in)activation is similar to the voltammetric time scale^[8] ${\displaystyle \tau =RT/F\nu }$. If a RDE is used, these slow (in)activations are detected by a hysteresis in the catalytic voltammogram that is not due to mass-transport. The hysteresis may disappear at very fast scan rates (if the inactivation has no time to proceed) or at very slow scan rates (if the (in)activation reaction reaches a steady-state).^[12]

3. Combining Protein Film Voltammetry and Spectroscopy

Conventional voltammetry offers a limited picture of the enzyme-electrode interface and on the structure of the species involved in the reaction. Complementing standard electrochemistry with other methods can provide a more complete picture of catalysis.^[13][14][15]