Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Janina Susanne Lütke Stockdiek
 -- 3265 2022-11-29 16:09:23 |
2 format correct
Catherine Yang
 -7 word(s) 3258 2022-11-30 03:00:39 | |
3 format correct
Catherine Yang
 + 16 word(s) 3274 2022-11-30 03:07:01 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Clever, L.;  Pohl, J.S.;  Bossek, J.;  Kerschke, P.;  Trautmann, H. Stream Classification Algorithms and Architectures. Encyclopedia. Available online: https://encyclopedia.pub/entry/37157 (accessed on 22 December 2024).
Clever L,  Pohl JS,  Bossek J,  Kerschke P,  Trautmann H. Stream Classification Algorithms and Architectures. Encyclopedia. Available at: https://encyclopedia.pub/entry/37157. Accessed December 22, 2024.
Clever, Lena, Janina Susanne Pohl, Jakob Bossek, Pascal Kerschke, Heike Trautmann. "Stream Classification Algorithms and Architectures" Encyclopedia, https://encyclopedia.pub/entry/37157 (accessed December 22, 2024).
Clever, L.,  Pohl, J.S.,  Bossek, J.,  Kerschke, P., & Trautmann, H. (2022, November 29). Stream Classification Algorithms and Architectures. In Encyclopedia. https://encyclopedia.pub/entry/37157
Clever, Lena, et al. "Stream Classification Algorithms and Architectures." Encyclopedia. Web. 29 November, 2022.
Stream Classification Algorithms and Architectures
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app12189094

Areas of stream classification are diverse—ranging, e.g., from monitoring sensor data to analyzing a wide range of (social) media applications. Research in stream classification is related to developing methods that adapt to the changing and potentially volatile data stream. It focuses on individual aspects of the stream classification pipeline, e.g., designing suitable algorithm architectures, an efficient train and test procedure, or detecting so-called concept drifts. 

data mining big data stream classification data stream analysis

1. Architecture

Commonly, the classifiers are divided regarding their architecture into single classifiers, or classifier structures, called ensembles [1][2]. To deal with large amounts of data and the changing data under certain circumstances, combining several models has proven beneficial rather than performing the classification based on a single classification model. A classifier ensemble is a collection of several weak learners, i.e., simple algorithms, whose accuracy is at least slightly above chance. The main focus is on algorithm efficiency, and the basic idea is that combining several weak learners, which only work on a few features, leads to better global classification accuracy. Research on the composition of the ensembles and the combination or weighting of the weak learners is controversial. In their work, Ref. [3] proposes different aspects, which should be considered when creating an ensemble.
The combination of classifiers describes how the individual classifiers interact with each other. Several approaches and voting strategies exist for weak learners [3]. A flat architecture (also found in literature as a bagging strategy) describes a setting where weak learners are trained in parallel on different data points and/or feature subsets, and their classification results are combined, e.g., via majority votes. Thereby, the most frequently predicted class is assigned to the respective instance. Alternatively, classification can be based on a single selected ensemble classifier or by weighting the different models [4] (Table 1).
Table 1. Overview of relevant stream classification algorithm review and benchmarking studies.
Ensemble Tree Neural Neighbor Rule Frequency SVM Benchmark
[5] ✓ ✓   ✓ ✓      
[6] ✓ ✓   ✓ ✓ ✓ ✓  
[7]   ✓ ✓ ✓ ✓   ✓  
[2] ✓ ✓ ✓ ✓   ✓ ✓ ✓
[8] ✓ ✓   ✓   ✓   ✓
[3] ✓              
[9] ✓ ✓   ✓ ✓      
[1] ✓ ✓ ✓ ✓        
[10] ✓              
[11] ✓ ✓ ✓     ✓   ✓
[12] ✓             ✓
[13]   ✓ ✓ ✓     ✓  
[14]     ✓          
[15]   ✓ ✓ ✓   ✓   ✓
[16] ✓ ✓ ✓ ✓   ✓    
[17] ✓ ✓   ✓       ✓
[18]       ✓       ✓
Another possibility is to use the results of the weak learner to train a meta learner (called stacking) [3]. Instances formed by the predictions of the weak learners are denoted as meta-dataset. Together with the initial labels of the training data, a meta-classifier can be induced, which is trained on predictions of weak learners as features. This model is then used to predict the label of a new observation.
Another important configuration aspect of classifier ensemble approaches is classifier diversity [3]. On the one hand, it is possible to train the individual classifiers on different features (vertical partitioning) or data points (horizontal partitioning). On the other hand, different hyperparameters of classifiers or even different base classifiers on the whole training data can be used. With all these possibilities, the diversity of ensembles is a multifaceted topic. Many studies, strategies, and metrics exist to achieve and monitor the appropriate level of diversity for ensembles [3]. Unlike offline, maintaining diversity and performance in the online setting is considerably more complex. This is especially the case for changing data streams (Ref. [10] gives a broad overview of ensemble algorithms in stream classification. They elaborate on the ensemble diversity and combination of base learners. Further, they give an overview of the suitability of algorithms in the case of imbalanced data, novelty class detection, active and semi-supervised learning, and high-dimensional data. The authors define future research directions as handling high dimensional data, the combination of multiple streams, and self-tuning ensembles. However, more work could be conducted to analyze the type of drift and work with imbalanced data and delayed label information. Ref. [19] analyze the impact of changes in the data stream on diversity measures in streaming scenarios. The analyses are based on the MOA framework and the artificial and real-world datasets provided in the MOA framework. This study demonstrates that diversity metrics can be used for stream classification. Further, the monitoring of ensemble diversity over time can be used to elaborate the type of concept drift .

2. Algorithms

Various algorithms can be found in the literature suitable for a stream classification problem. In line with the review papers in the field, the most common solutions are based on the ideas of trees, neural networks-, frequency-, and neighborhood-based approaches [15][16]. In addition, Support Vector Machines and rule-based algorithms are frequently mentioned, as they can be adapted to the stream setting [2][7]. An overview of the most common techniques will be described (see Figure 1).
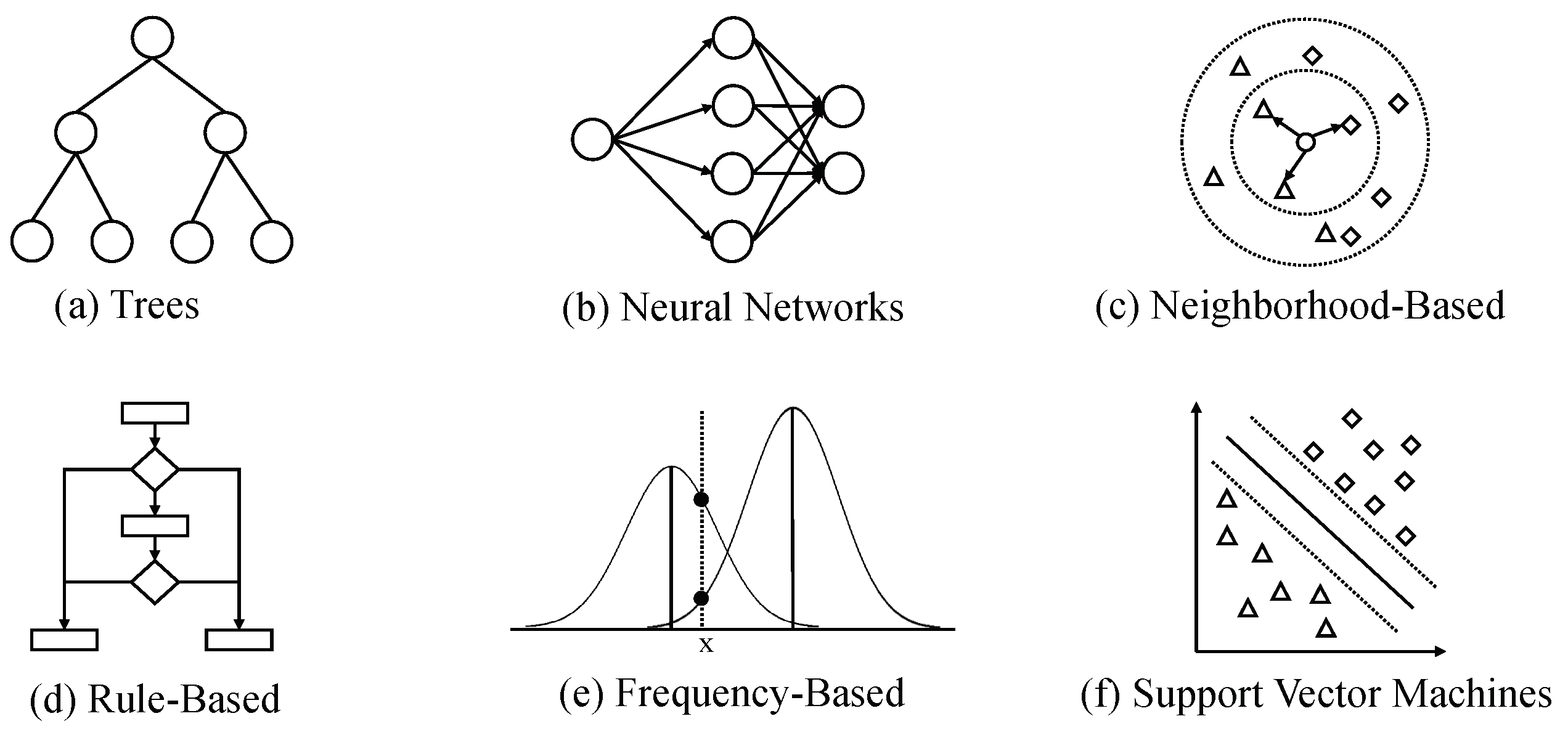
Figure 1. Overview of the most common algorithm types used in the reviewed literature in a stream classification scenario. The point shapes in (c) and (f) represent data of different classes.

2.1. Trees

Tree-based algorithms (see Figure 1a) are suitable for stream classification scenarios because of their low computational costs, their ability to deal with redundant features, and their robustness in terms of noisy data [2]. Hoeffding Trees, as a particular class of decision trees, are one of the most fundamental algorithms in the field [20]. The underlying concept is a very fast decision tree (VFDT) algorithm. With this algorithm, it is not necessary to consider an exhaustive training database but a sufficiently large subset at each splitting point of the tree. Moreover, instances are not stored as such but with the help of counters. Counters enumerate how many instances are classified according to a particular tree branch. Thus, the tree is generated incompletely but with a sufficiently large amount of information. By this, the algorithm perfectly fits the stream scenario, where training data might be incomplete at the beginning, not all instances can be stored, and predictions need to be made in time. 
For experimental studies, the SAMOA framework can be used to parallelize the vertical Hoeffding Tree (VHT) to cope with the high data volumes in stream classification scenarios [21]. VHT splits observations into feature subsets (vertical parallelism) of an instance. The algorithm treats all feature subsets as an independent. Thus, computations can be conducted in parallel. Ref. [12] evaluate ensemble methods on MOA real-world datasets. Specifically, they compared ensembles, which are trained online and window-based. They conclude that the adaptive window online ensemble (AWOE), introduced by [22], which operates in a hybrid fashion and includes an internal change detector, produced the best results in terms of accuracy, memory usage, and processing time.
Trees in terms of ensemble classifiers are called forests. The best-known variant—random forests—consists of several randomly generated decision trees. Each tree is trained on a random sample of the data and a subset of features (bagging). The classification results of the trees are merged into a prediction, e.g., via a majority vote, within the combination step.
To cope with the circumstances of the streaming scenario, the Adaptive Random Forest algorithm (ARF) includes a dynamic update method to react to possible changes in the data stream [23]. Each tree is provided with a change detection functionality so that new and more suitable trees can be built in the background at any time. In a large-scale study, the authors show the performance of ARF algorithms on different synthetic and real-world datasets with concept drift. For their experiments, they use the MOA framework. The evaluation criteria within their experiments are classification accuracy, CPU Time, and Memory usage. The authors show that adaptive random forests perform exceptionally well on real-world data sets with label delay. Further, the algorithm is suitable for settings with many features, e.g., in a Natural Language Processing setting such as spam email detection. Here, the authors demonstrate good results even when using a small number of decision trees. Additionally, within the ARF approach, it is possible to train the trees in parallel without harming the model’s classification performance. The algorithm is especially suitable for classification problems, where a subset of features is sufficient to create a decisive explanatory model. A drawback of tree-based classification models is that rebuilding, e.g., changing data, is a time-consuming task [6]. Further, trees tend to over-fit in case they create a high number of branches with only small leafs.

2.2. Neural Network

Due to their generalizability and ability to solve non-linear and dynamic decision problems, neural network-based methods (see Figure 1b) are standard in the field [2]. One of the best-known neural network-based methods in the field of stream classification is the extreme learning machine (ELM) [14]. The classical ELM is a learning algorithm conducted on feed-forward neural network(s) with a single hidden layer [24]. The algorithm provides high generalization performance and is very efficient because it does not require gradient-based back-propagation to work. The hidden nodes, as well as their weights and biases, are chosen randomly. Only the weights of the hidden nodes to the output layer must be learned by a least squares method.
Since the invention of the ELM in 2004, it has been used and further developed in many applications. In their review paper, ref. [14] describe the development of the algorithm and show the different works and modifications that have emerged around the basic idea of this efficient and straightforward approach. While the original ELM was designed for batch learning, the Online Sequential ELM (OS-ELM) algorithm can be trained online on single new data points or flexible batch sizes [25]. Based on the OS-ELM, many extensions and solutions have been developed. The individual works deal with the problems of concept drift, unbalanced distribution of classes, and uncertainty of data [14].
Next to the ELM, other neural network-based approaches were proposed in the literature. Ref. [26] shows a wide-ranging benchmarking study for neural network algorithms on stream data. Concretely, they compare a basic Multi-Layer Perceptron (MLP) model with a Long-Short Term Memory network (LSTM), a Convolutional Neural Network (CNN), and a Temporal Convolutional Network (TCN). The models are evaluated in terms of accuracy and computational efficiency on various UCI repository datasets, including image, sensor, and motion datasets. The authors conclude that CNNs reach the best accuracy by allowing fast processing of the incoming data stream. LSTM and TCN lag behind the capabilities in terms of higher processing time and worse performance.
CNNs are broadly used in high-dimensional data, as in image and video analysis. Intelligent filtering and reduction of the input data make it possible to classify images or detect objects in the images efficiently. Application scenarios are, e.g., gesture recognition procedures, surveillance applications, or the automatic analysis of ultrasound [27][28][29][30].
More complex neural networks are at a disadvantage in the stream setting because most methods cannot make predictions in real-time [16]. Nevertheless, researchers thrive on using state-of-the-art methods’ advantages on data streams. A specific example is a generative adversarial network (GAN) proposal by [31]. The deep learning architecture can regenerate training data and overcome data storing limitations. Due to the high computational costs of training and their need for extensive parameter tuning, deep learning methods are not commonly approved in evolving data streams [16]. Next to their high complexity, neural network-based methods are often criticized as black boxes, as the decisions are not interpretable [2].

2.3. Neighborhood Based

Neighborhood-based methods (see Figure 1c) are frequently used in the stream classification setting. As one of the most common approaches, the k-nearest Neighbor (kNN) algorithm predicts labels of new data records by selecting the class label of the closest training instance [6]. For k>1, the class label is defined as the majority of all k nearest neighbors of the instance.
Nearest neighbor classifiers can be naturally transformed to the incremental setting by selecting a limited subset of the most “useful” examples (also called reservoir sampling or lazy learning [1][6]. The sampling process can be biased or unbiased [7]. In biased methods, the time component of data streams is considered. Thus, more recent data points are weighted higher than earlier data records, especially suited for streams with concept drifts. Although the algorithm is intuitive, determining the appropriate k, especially when considering evolving data streams, is not trivial. The ANNCAD algorithm is one of the earliest kNN algorithms designed explicitly for data streams [32]. Here, an adaptive choice of the number of k nearest neighbors is possible.
Similar to traditional nearest-neighbor approaches, classification can also be conducted based on clusters. Original training data is represented as, e.g., the centroid of supervised microclusters. Thus, the data, as well as computational costs, are reduced [7]. A class consists of one or more micro-clusters, and predictions are derived by measuring the distance of newly arriving instances to the centroids of clusters. Classification of instances based on micro-clusters is also reported by [5] as an on-demand classification. Another common technique, aligned with the one above, is representing data points as density regions in a grid [33][34]. The idea of grid-based clusters is that only counters of the grid regions need to be stored instead of complete observations. Ref. [35] proposes an ensemble of k-means classifiers—called Semi-Supervised Adaptive Novel Class Detection and Classification (SAND). Each classifier is trained on a different batch of data. The data of each batch is partially labeled and can be determined dynamically. New labeled instances are gained using records with a high classification confidence score to handle concept drifts. Thus, the classifier is updated. Further, a dense area of outliers is interpreted as a new class. Within their study, the authors compared their algorithms with, e.g., Adaptive Hoeffding Trees in terms of its classification performance and ECSMiner, (ECSMiner is a novel class detection algorithm, proposed by [36].) for the novel class detection component. The performance of SAND in both tasks is at least comparable to the considered algorithms, with only a small number of labels.
The challenges of neighborhood-based approaches are the reduction of processing time, the development of meaningful cluster splitting methods, and the curse of dimensionality [16].

2.4. Rule-Based

An intuitive classification approach is rule-based systems [5][8][9]. The idea is that combinations of different features indicate a class label (see Figure 1d). For instance, specific intervals of numerical attributes are associated with a respective class. Thus, traditional rule-based methods cannot be used in stream scenarios with evolving feature spaces or other changes in the data. Exemplary algorithms extending the idea of rule-based systems to the streaming scenario are, e.g., STAGGER, FLORA, and AQ-PM [6]. STAGGER consists of two stages to handle shifts in the distribution: in the first step, the weights of the features, which lead to the applied rules, are adjusted. Second, new features are added to existing rules [37]. FLORA (as well as the extension FLORA3) is based on the idea of temporal windowing [38]. A collection of temporal contexts can be disabled or enabled over time, e.g., to handle seasonal drifts. The AQ-PM approach keeps only the training data close to the rules’ decision boundaries [39]. Thus, AQ-PM can learn new concepts by forgetting older examples. However, the major drawbacks of rule-based systems are their inflexibility and low learning speed [6].

2.5. Frequency-Based

The Naïve Bayes algorithm (NB) is an incremental algorithm, which is by nature able to handle data streams [6]. Decisions are made based on a frequency scheme (see Figure 1e). Concretely, NB is based on the Bayes Theorem, which assumes that the explanatory variables are independent conditionally of the target variable [40]. Thus, Naïve Bayes works intrinsically incremental by updating relevant entries in its probability table and deriving predictions based on posterior probabilities whenever a new training instance arrives. The algorithm is well-known for its simplicity and can predict class memberships with low computational costs. The traditional algorithm deals with a discretized feature space. However, numerical feature spaces occur often, e.g., in sensor data. Bayesian classification can be combined with an initial discretization step as preprocessing, e.g., via the PiD method [41]. An option of using the algorithm on continuous data arises from the Gaussian Bayes models [11]. Nevertheless, the two main drawbacks of Bayes classifiers are the independence assumption of the features, such as the inability to handle multimodal distributions.

2.6. Support Vector Machines

The Support Vector Machine (SVM) [2] is a well-known offline classification algorithm. SVMs are based on finding the maximum marginal hyperplane that separates training data of different classes (see Figure 1f). Finding the hyperplane is a convex optimization problem, which can be solved using the Lagrangian formulation. Using SVM algorithms in big data settings comes with complex calculations, making the traditional SVM unsuitable for the stream scenario. An approach that adapts the idea of the SVM algorithm to the stream classification problem is the Core Vector Machine (CVM) [42]. Here, a minimum enclosing hypersphere is used, which represents the divisive data records. Calculations are then based on the representative hypersphere instead of the original data records, making calculations more efficient. This idea forms the basis for other SVM-based algorithms such as StreamSVM [43]. Here, the CVM is extended so that one pass over the data instances is sufficient. The main drawback of the SVM is the low learning and prediction speed, such as the inability to react to changes in the data stream. Further, SVM models are extremely difficult to interpret [6]. Further, the performance of SVM-based classification models depends on a proper parametrization, e.g., choosing a suitable Kernel [2].

3. Specific Classification Problems

In the first case, an observation   x → ∈ X is classified into an l-dimensional space Y = { C 1 , … , C l }  of l≥3 classes. A common way to deal with multi-class problems is the one-vs-all principle, which is based on l binary classification models [44] (one model per class). Each of them is generated using labeled instances of the respective class of interest on the one hand (1) and the instances of all remaining classes on the other (0). It should be noted that nowadays, various classification algorithms—e.g., neighborhood-based methods, or trees—can deal with more than two classes by nature.
In the case of multi-label problems, instances will not only be assigned one but several classes simultaneously. That is, the feature vector of the i-th observation remains a p-dimensional vector x → i = ( x i 1 , … , x i p ) ∈ X . However, extending the previous notation, the corresponding outcome will no longer be a single class label yi∈Y, but instead, a k-dimensional vector  y → i = ( y i 1 , … , y i k ) ∈ ( Y 1 × … × Y k ) , where each element y i j ∈ Y j , j=1,…,k, maps to its own finite set Yj of lj class labels.
The following approaches are common when dealing with Multi-Label problems: First, multi-label problems can be separated into several binary problems (called binary relevance), meta labels of label combinations (called label power sets), and a set of label pairs (called pairwise). These approaches are referred to as problem transformation. The appropriate strategy depends on the data basis. Binary relevance is an easy-to-understand method, which is often implemented in the context of ensemble models. A disadvantage of this method is that no label correlations are considered here, i.e., each label is assigned independently of all other labels. On the other hand, label correlations are considered within the label powerset approach. Here, however, the focus is on essential interactions to counteract the sparsity of data points and achieve a meaningful classification, e.g., by selecting important label correlations [45]. The pairwise approach is rarely used in online settings due to its high computational complexity in large-scale multi-label problems.
Another possibility for dealing with non-binary problems is extending the classification algorithms (such as decision trees). One example is the extension of the Hoeffding Tree algorithm [46]. Here, leaf nodes exist for every necessary label combination in the label powerset.
For a comprehensive overview of multi-label stream classification, the researchers refer to the survey paper by [47]. They discuss a wide range of multi-label stream classification algorithms, their ability to adapt to changes in the data stream, and standard multi-label datasets. As an evaluation criterion, the authors analyzed the algorithm performance in terms of the F1 metric and the running time. By benchmarking multiple algorithms on different real-world and synthetic data sets, they give a good overview of the strengths and weaknesses of the individual approaches. The authors conclude that a Multi-Label ensemble with Adaptive Windowing (MLAW), proposed by, shows the best classification performance and efficiency results. The authors conclude that there is room for further research on handling and detecting different types of concept drift, imbalanced classes, and temporal dependencies of labels.

References

  1. Stefanowski, J.; Brzezinski, D. Stream Classification. In Encyclopedia of Machine Learning and Data Mining; Springer: Boston, MA, USA, 2017; pp. 1191–1199.
  2. Nguyen, H.L.; Woon, Y.K.; Ng, W.K. A Survey on Data Stream Clustering and Classification. Knowl. Inf. Syst. 2015, 45, 535–569.
  3. Gomes, H.M.; Barddal, J.P.; Enembreck, F.; Bifet, A. A Survey on Ensemble Learning for Data Stream Classification. ACM Comput. Surv. (CSUR) 2017, 50, 23.
  4. Pan, S.; Zhang, Y.; Li, X. Dynamic Classifier Ensemble for Positive Unlabeled Text Stream Classification. Knowl. Inf. Syst. 2012, 33, 267–287.
  5. Gaber, M.M.; Zaslavsky, A.; Krishnaswamy, S. A Survey of Classification Methods in Data Streams. In Data Streams; Advances in Database Systems; Aggarwal, C.C., Ed.; Springer: Boston, MA, USA, 2007; Volume 31, pp. 39–59.
  6. Lemaire, V.; Salperwyck, C.; Bondu, A. A Survey on Supervised Classification on Data Streams. Bus. Intell. 2014, 4, 88–125.
  7. Aggarwal, C.C. A Survey of Stream Classification Algorithms. In Data Classification: Algorithms and Applications; Charu, C., Aggarwal, V.K., Eds.; CRC Press: New York, NY, USA, 2014; Chapter 9; pp. 245–274.
  8. Barddal, J.P.; Gomes, H.M.; de Souza Britto, A.; Enembreck, F. A benchmark of classifiers on feature drifting data streams. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2180–2185.
  9. Janardan; Mehta, S. Concept drift in Streaming Data Classification: Algorithms, Platforms and Issues. Procedia Comput. Sci. 2017, 122, 804–811.
  10. Krawczyk, B.; Minku, L.L.; Gama, J.; Stefanowski, J.; Woźniak, M. Ensemble learning for data stream analysis: A survey. Inf. Fusion 2017, 37, 132–156.
  11. Losing, V.; Hammer, B.; Wersing, H. Incremental on-line learning: A review and comparison of state of the art algorithms. Neurocomputing 2018, 275, 1261–1274.
  12. Nagendran, N.; Sultana, H.P.; Sarkar, A. A Comparative Analysis on Ensemble Classifiers for Concept Drifting Data Streams. In Soft Computing and Medical Bioinformatics; SpringerBriefs in Applied Sciences and Technology; Springer: Singapore, 2019; pp. 55–62.
  13. Srivani, B.; Sandhya, N.; Padmaja Rani, B. Literature review and analysis on big data stream classification techniques. Int. J. Knowl.-Based Intell. Eng. Syst. 2020, 24, 205–215.
  14. Li, L.; Sun, R.; Cai, S.; Zhao, K.; Zhang, Q. A Review of Improved Extreme Learning Machine Methods for Data Stream Classification. Multimed. Tools Appl. 2019, 78, 33375–33400.
  15. Khannouz, M.; Glatard, T. A Benchmark of Data Stream Classification for Human Activity Recognition on Connected Objects. Sensors 2020, 20, 6486.
  16. Bahri, M.; Bifet, A.; Gama, J.; Gomes, H.M.; Maniu, S. Data stream analysis: Foundations, major tasks and tools. WIREs Data Min. Knowl. Discov. 2021, 11, e1405.
  17. Din, S.U.; Shao, J.; Kumar, J.; Mawuli, C.B.; Mahmud, S.M.H.; Zhang, W.; Yang, Q. Data Stream Classification with Novel Class Detection: A Review, Comparison and Challenges. Knowl. Inf. Syst. 2021, 63, 2231–2276.
  18. Tieppo, E.; Santos, R.R.d.; Barddal, J.P.; Nievola, J.C. Hierarchical classification of data streams: A systematic literature review. Artif. Intell. Rev. 2021, 54, 1–40.
  19. Brzezinski, D.; Stefanowski, J. Ensemble Diversity in Evolving Data Streams. In Proceedings of the International Conference on Discovery Science, Bari, Italy, 19–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 229–244.
  20. Domingos, P.; Hulten, G. Mining High-Speed Data Streams. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; ACM: New York, NY, USA, 2000; pp. 71–80.
  21. Kourtellis, N.; Morales, G.D.F.; Bifet, A.; Murdopo, A. VHT: Vertical Hoeffding Tree. In Proceedings of the International Conference on Big Data, Washington, DC, USA, 5–8 December 2016; pp. 915–922.
  22. Sun, Y.; Wang, Z.; Liu, H.; Du, C.; Yuan, J. Online Ensemble Using Adaptive Windowing for Data Streams with Concept Drift. Int. J. Distrib. Sens. Netw. 2016, 12, 4218973.
  23. Gomes, H.M.; Bifet, A.; Read, J.; Barddal, J.P.; Enembreck, F.; Pfharinger, B.; Holmes, G.; Abdessalem, T. Adaptive Random Forests for Evolving Data Stream Classification. Mach. Learn. 2017, 106, 1469–1495.
  24. Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990.
  25. Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423.
  26. Lara-Benítez, P.; Carranza-García, M.; Martínez-Álvarez, F.; Santos, J.C.R. On the Performance of Deep Learning Models for Time Series Classification in Streaming. In Proceedings of the 15th International Conference on Soft Computing Models in Industrial and Environmental Applications, Burgos, Spain, 16–18 September 2020; Springer: Cham, Switzerland, 2020; pp. 144–154.
  27. Kumar, E.K.; Kishore, P.; Kumar, M.T.K.; Kumar, D.A. 3D Sign Language Recognition with Joint Distance and Angular Coded Color Topographical Descriptor on a 2–Stream CNN. Neurocomputing 2020, 372, 40–54.
  28. Krishnaveni, P.; Sutha, J. Novel Deep Learning Framework for Broadcasting Abnormal Events Obtained From Surveillance Applications. J. Ambient Intell. Humaniz. Comput. 2020, 11, 4123.
  29. Elboushaki, A.; Hannane, R.; Afdel, K.; Koutti, L. xMultiD-CNN: A Multi-Dimensional Feature Learning Approach Based on Deep Convolutional Networks for Gesture Recognition in RGB-D Image Sequences. Expert Syst. Appl. 2020, 139, 112829.
  30. Lin, Z.; Li, S.; Ni, D.; Liao, Y.; Wen, H.; Du, J.; Chen, S.; Wang, T.; Lei, B. Multi-Task Learning for Quality Assessment of Fetal Head Ultrasound Images. Med. Image Anal. 2019, 58, 101548.
  31. Besedin, A.; Blanchart, P.; Crucianu, M.; Ferecatu, M. Deep Online Classification Using Pseudo-Generative Models. Comput. Vis. Image Underst. 2020, 201, 103048.
  32. Law, Y.N.; Zaniolo, C. An Adaptive Nearest Neighbor Classification Algorithm for Data Streams. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Porto, Portugal, 3–7 October 2005; Jorge, A.M., Torgo, L., Brazdil, P., Camacho, R., Gama, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 108–120.
  33. Sethi, T.S.; Kantardzic, M.; Hu, H. A Grid Density Based Framework for Classifying Streaming Data in the Presence of Concept Drift. J. Intell. Inf. Syst. 2016, 46, 179–211.
  34. Tennant, M.; Stahl, F.; Rana, O.; Gomes, J.B. Scalable Real-Time Classification of Data Streams with Concept Drift. Future Gener. Comput. Syst. 2017, 75, 187–199.
  35. Haque, A.; Khan, L.; Baron, M. SAND: Semi-Supervised Adaptive Novel Class Detection and Classification over Data Stream. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1652–1658.
  36. Masud, M.M.; Gao, J.; Khan, L.; Han, J.; Thuraisingham, B. Classification and Novel Class Detection in Data Streams with Active Mining. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Hyderabad, India, 21–24 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 311–324.
  37. Schlimmer, J.C.; Granger, R.H. Incremental Learning from Noisy Data. Mach. Learn. 1986, 1, 317–354.
  38. Widmer, G.; Kubat, M. Learning in the presence of concept drift and hidden contexts. Mach. Learn. 1996, 23, 69–101.
  39. Maloof, M.A.; Michalski, R.S. Selecting examples for partial memory learning. Mach. Learn. 2000, 41, 27–52.
  40. Bayes, T. LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418.
  41. Gama, J.A.; Pinto, C. Discretization from Data Streams: Applications to Histograms and Data Mining. In Proceedings of the 2006 ACM Symposium on Applied Computing, Dijon, France, 23–27 April 2006; ACM: New York, NY, USA, 2006; pp. 662–667.
  42. Tsang, I.W.; Kocsor, A.; Kwok, J.T. Simpler Core Vector Machines with Enclosing Balls. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; ACM: New York, NY, USA, 2007; pp. 911–918.
  43. Rai, P.; Daumé, H.; Venkatasubramanian, S. Streamed Learning: One-Pass SVMs. In Proceedings of the 21st International Jont Conference on Artifical Intelligence, Pasadena, CA, USA, 11–17 July 2009; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2009; pp. 1211–1216.
  44. Hashemi, S.; Yang, Y.; Mirzamomen, Z.; Kangavari, M. Adapted One-Versus-All Decision Trees for Data Stream Classification. IEEE Trans. Knowl. Data Eng. 2008, 21, 624–637.
  45. Read, J.; Pfahringer, B.; Holmes, G. Multi-Label Classification Using Ensembles of Pruned Sets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 995–1000.
  46. Read, J.; Bifet, A.; Holmes, G.; Pfahringer, B. Scalable and Efficient Multi-Label Classification for Evolving Data Streams. Mach. Learn. 2012, 88, 243–272.
  47. Zheng, X.; Li, P.; Chu, Z.; Hu, X. A Survey on Multi-Label Data Stream Classification. IEEE Access 2019, 8, 1249–1275.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Artificial Intelligence
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Lena Clever
,
Janina Susanne Pohl
,
Jakob Bossek
,
Pascal Kerschke
,
Heike Trautmann
View Times: 690
Revisions: 3 times (View History)
Update Date: 30 Nov 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback