Flow-Induced Vibration

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Fue-Sang Lien	--	1436	2022-11-29 09:26:17	\|
2	format correct	Conner Chen	+ 5 word(s)	1441	2022-11-30 09:36:11	\| \|
3	format correct	Conner Chen	Meta information modification	1441	2022-12-01 01:50:29	\|

This entry is adapted from the peer-reviewed paper 10.3390/en15228719

Flow-induced vibration (FIV) of bluff body structures is a classical bidirectional flow–structure interaction problem, which is linked to various fluid dynamics phenomena (e.g., boundary-layer separation, vortex formation and shedding, hydrodynamic loading on the structures) as well as structure vibrations.

flow-induced vibration mathematical modelling numerical modelling

1. Fundamental Concepts and Background of FIV

Flow-induced vibration refers to the alternating motion of a structure due to the aerodynamic force exerted by a moving fluid over the body surface. The flow regime that results is significantly affected by this structural motion—in consequence, flow-induced vibration (FIV) is a classical bidirectional fluid–structure interaction (FSI) problem.

In 1977, Blevins ^[1] first coined the term “FIV” and classified FIV mechanisms according to steady and unsteady flow conditions. In a steady flow, the interaction of the fluid and structure always has a fixed pattern which is predictable. On the other hand, an unsteady FSI can involve either random patterns dominated by transient forces (e.g., turbulence and sudden changes of the flow), or very regular patterns generated by a known excitation (e.g., forced vibration). Nakamura et al. ^[2] further identified two-phase flow where the changes of flow momentum and pressure over time are the major causes of the structural vibration. Among these flow regimes, the two-way interactive impact of fluid and structure in a steady single-phase flow is the most common case investigated, where the mechanisms responsible for FIV can be further classified into two general categories based on the source of the unsteady forces (viz., resonance-type and instability-type) ^[2].

The resonance-type structural oscillation is essentially a kind of forced vibration, which is typically driven by external oscillatory forces arising from multiple sources, such as vortex shedding behind the structure (VIV) and vibrations in the incoming (incident) flow (buffeting). When the fluctuation frequency of external excitation is very close to the natural frequency of the structure, a resonance response may occur resulting in a much larger amplitude in the oscillations. By comparison, if some initial unsteady flow-induced forces are applied to the body to make it move first, the moving body will induce a periodically hydrodynamic force on itself. The motion-induced force and oscillating system mutually reinforce each other until a dynamic equilibrium is reached—a phenomenon that is referred to as an instability-type oscillation. In other words, the structure undergoing an instability response requires an initial small disturbance to begin the motion and then this motion is gradually converted to significant periodic oscillations autonomously—this is similar to a self-excited motion with no upper limit in the amplitude of vibration. These representative instabilities include galloping and flutter ^[3]. These four common forms of FIV will be explained in detail below.

2. Vortex-Induced Vibration

As a resonance-type response, the well-known vortex-induced vibration is generated by unsteady aerodynamic forces exerted by the fluid on an immersed structure. When a viscous flow passes over an elastically-supported rigid body, a boundary layer forms and then separates from near the rear of the body. This action results in vortex shedding from either side of the body producing a von Kármán vortex street in the wake. This alternate vortex shedding from the back of the body causes an asymmetric pressure distribution on body surface giving rise to the fluid forces responsible for VIV of the bluff body ^[1].

“Lock-in” or synchronization occurs when the vortex-shedding frequency

f_{v s}

is approximately equal to the structural natural frequency

f_{n}

. This results in a resonant oscillation of the body that is characterized by a larger but, nevertheless, limited vibration amplitude. The phenomenon of lock-in occurs for a certain range of inflow (incident) wind speeds (cf. left panel of Figure 1). From these considerations, VIV is an inherently self-governed, self-regulated, and self-limiting phenomenon which can occur in one- or multi-degree-of-freedom dynamical systems. In addition to the “lock-in” phenomenon, VIV also exhibits various forms of stronger non-linear oscillatory behavior. These include resonance delay (where the amplitude of vibration reaches its maximum at a velocity greater than the resonance velocity

U_{R} \equiv f_{n} D / S_{t}

where

S_{t}

is the Strouhal number and D is a characteristic length of the structure), hysteresis (producing different amplitude responses as the flow speed is increased or decreased), and a multi-valued response (where a given fixed velocity can result in multiple values for the vibration amplitude) ^[4].

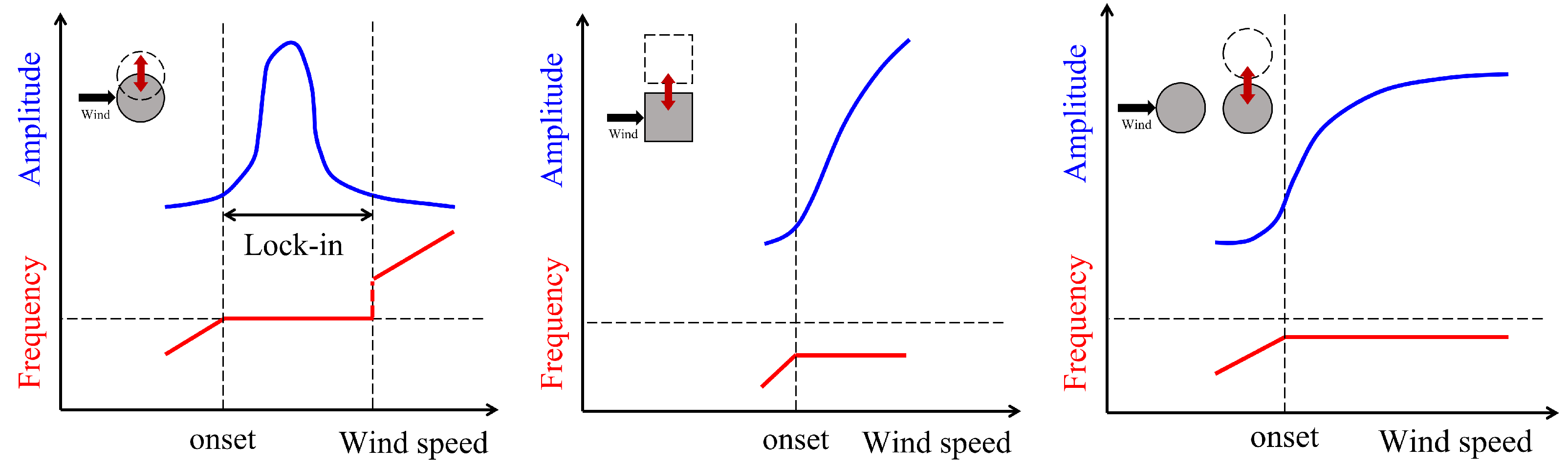
Figure 1. Comparison of amplitude-velocity and frequency-velocity of FIV phenomenon: VIV (left); instability like galloping and flutter (middle); and, wake galloping (right).

The dynamical characteristics of lock-in makes VIV an ideal choice for fluid energy harvesting. More specifically, a VIV-based energy converter exhibits a better power performance and a higher energy efficiency when the incoming (incident) wind speed lies in the synchronization range ^[5].

3. Buffeting

Buffeting is also a resonance-type response, but the resonance results from a fluctuating incoming (incident) flow rather than from a vortex-related instability as in the “lock-in” phenomenon. As an example, the fluctuations in the incident flow can arise from the natural atmospheric turbulence as is commonly observed in long-span bridges ^[6] or from the oscillating wake generated by structures upstream of a bluff body as in multi-body system—this phenomenon is also referred to as wake galloping ^[3] (cf. right panel of Figure 1). Investigations undertaken with regard to bridge structures and aeronautics have shown that a buffeting response may occur even at low wind speeds, accompanied by a smaller oscillation amplitude and a wider frequency range than that obtained from VIV ^[3].

These characteristics suggest that buffeting can be utilized to harness fluid energy in a multi-body design and the power performance from such a design is expected be strongly dependent on the precise layout (arrangement) of the various oscillating bodies.

4. Galloping

As a representative instability response, a body subjected to galloping will first undergo a very small oscillatory motion induced by an initial perturbation. These motions result subsequently in significant oscillations once a critical incident flow velocity is exceeded (cf. middle panel of Figure 1). Galloping can occur in the transverse direction for an elastically-mounted body or in torsion for an hinged body. Torsional galloping is a much more complex phenomenon in terms of the angle of attack, the angular displacement and velocity, the phase difference and other complex dynamics involving rotational motion. It is noted that torsional galloping is not as common as transverse galloping in the context of actual engineering applications ^[7]. In consequence, only transverse galloping will be discussed in these contents—for simplicity, transverse galloping will be referred to as galloping hereafter.

After the onset of galloping, the vibration amplitude will increase monotonically with the increasing flow velocity and will not come to rest again even at very large flow velocities. This is the most distinct difference between instability and resonance. Galloping is associated with a much lower vibration frequency than that of vortex shedding. The characteristics of a monotonically increasing amplitude with increasing flow velocity amplitude and a frequency that is not determined by any form of lock-in is what fundamentally distinguishes a galloping (or instability) phenomenon from a resonance (VIV) phenomenon.

In general, galloping is considered to have a greater energy potential in terms of energy harvesting than VIV owing to its much larger vibration amplitudes and extended range of wind speeds for which galloping occurs, once the critical velocity for onset is exceeded. Moreover, galloping occurs only for cylinders with specific cross-sectional shapes (e.g., square, rectangular, D-section) or for cylinder–appendage systems (e.g., cylinder with an attached splitter plate)—indeed, galloping does not occur for flow past a circular cylinder. As a consequence, an energy converter utilizing galloping will require a special geometrical design in order to allow the occurrence of galloping or of the interaction of VIV and galloping.

5. Flutter

Flutter is also a typical non-self-limited and self-sustained fluid instability usually applicable to dynamical systems involving two or more degree of freedoms. This phenomenon is closely related to the coupling of resonant bending and torsion deformation of a body, and has some common features with galloping.

Figure 1 compares the oscillation characteristics of VIV, galloping, flutter, and wake galloping in terms of the amplitude and frequency response. As shown, all of these oscillatory phenomena have a threshold flow speed for onset—the wind speed for VIV onset is lower than that for galloping and flutter. Only VIV exhibits a lock-in of frequency and a limited displacement—the other forms of flow-induced vibration are non-self-limiting with respect to the oscillation amplitude and are associated with a frequency lower than the natural structural frequency. As discussed previously, FIV exhibits a complex taxonomy—each category in the classification corresponds to a different generating mechanism and is associated with different response modes. Furthermore, the vibration of a given bluff body can exhibit a number of different resonances and/or instabilities ^[2].

References

Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold Company: New York, NY, USA, 1977.
Nakamura, T.; Kaneko, S.; Inada, F.; Kato, M.; Ishihara, K.; Nishihara, T.; Mureithi, N.W.; Langthjem, M.A. Flow-Induced Vibrations: Classifications and Lessons from Practical Experiences; Butterworth-Heinemann: Portsmouth, NH, USA, 2013.
Rostami, A.B.; Armandei, M. Renewable energy harvesting by vortex-induced motions: Review and benchmarking of technologies. Renew. Sustain. Energy Rev. 2017, 70, 193–214.
Tamura, Y. Mathematical models for understanding phenomena: Vortex-induced vibrations. Jpn. Archit. Rev. 2020, 3, 398–422.
Wang, J.; Geng, L.; Ding, L.; Zhu, H.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902.
Su, Y.; Di, J.; Li, S.; Jian, B.; Liu, J. Buffeting response prediction of long-span bridges based on different wind tunnel test techniques. Appl. Sci. 2022, 12, 3171.
Luongo, A.; Piccardo, G. Linear instability mechanisms for coupled translational galloping. J. Sound Vib. 2005, 288, 1027–1047.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Physics, Fluids & Plasmas

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ying Wu

Zhi Cheng

Ryley McConkey

Fue-Sang Lien

Eugene Yee

View Times: 1.3K

Update Date: 01 Dec 2022

Table of Contents

Video Upload Options

Confirm