
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Camila Xu | -- | 3365 | 2022-11-28 01:32:36 |
Video Upload Options
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle. Fat objects are especially important in computational geometry. Many algorithms in computational geometry can perform much better if their input consists of only fat objects; see the applications section below.
1. Global Fatness
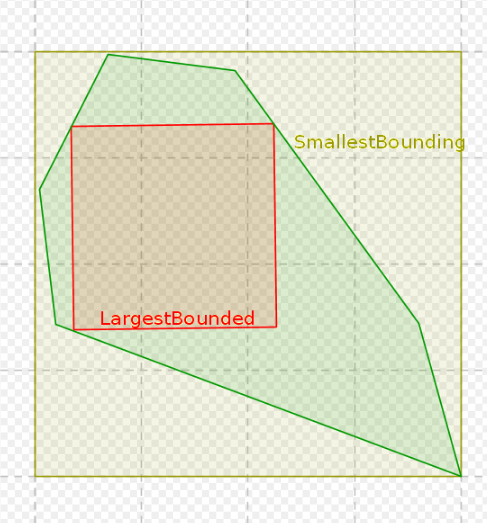
Given a constant R≥1, an object o is called R-fat if its "slimness factor" is at most R. The "slimness factor" has different definitions in different papers. A common definition[1] is:
- [math]\displaystyle{ \frac{\text{side of smallest cube enclosing} \ o}{\text{side of largest cube enclosed in} \ o} }[/math]
where o and the cubes are d-dimensional. A 2-dimensional cube is a square, so the slimness factor of a square is 1 (since its smallest enclosing square is the same as its largest enclosed disk). The slimness factor of a 10-by-1 rectangle is 10. The slimness factor of a circle is √2. Hence, by this definition, a square is 1-fat but a disk and a 10×1 rectangle are not 1-fat. A square is also 2-fat (since its slimness factor is less than 2), 3-fat, etc. A disk is also 2-fat (and also 3-fat etc.), but a 10×1 rectangle is not 2-fat. Every shape is ∞-fat, since by definition the slimness factor is always at most ∞.
The above definition can be termed two-cubes fatness since it is based on the ratio between the side-lengths of two cubes. Similarly, it is possible to define two-balls fatness, in which a d-dimensional ball is used instead.[2] A 2-dimensional ball is a disk. According to this alternative definition, a disk is 1-fat but a square is not 1-fat, since its two-balls-slimness is √2.
An alternative definition, that can be termed enclosing-ball fatness (also called "thickness"[3]) is based on the following slimness factor:
- [math]\displaystyle{ \left(\frac{\text{volume of smallest ball enclosing} \ o}{\text{volume of} \ o}\right)^{1/d} }[/math]
The exponent 1/d makes this definition a ratio of two lengths, so that it is comparable to the two-balls-fatness.
Here, too, a cube can be used instead of a ball.
Similarly it is possible to define the enclosed-ball fatness based on the following slimness factor:
- [math]\displaystyle{ \left(\frac{\text{volume of} \ o}{\text{volume of largest ball enclosed in} \ o}\right)^{1/d} }[/math]
1.1. Enclosing-Fatness vs. Enclosed-Fatness
The enclosing-ball/cube-slimness might be very different from the enclosed-ball/cube-slimness.
For example, consider a lollipop with a candy in the shape of a 1×1 square and a stick in the shape of a b×(1/b) rectangle (with b>1>(1/b)). As b increases, the area of the enclosing cube (≈b2) increases, but the area of the enclosed cube remains constant (=1) and the total area of the shape also remains constant (=2). Thus the enclosing-cube-slimness can grow arbitrarily while the enclosed-cube-slimness remains constant (=√2). See this GeoGebra page for a demonstration.
On the other hand, consider a rectilinear 'snake' with width 1/b and length b, that is entirely folded within a square of side length 1. As b increases, the area of the enclosed cube(≈1/b2) decreases, but the total areas of the snake and of the enclosing cube remain constant (=1). Thus the enclosed-cube-slimness can grow arbitrarily while the enclosing-cube-slimness remains constant (=1).
With both the lollipop and the snake, the two-cubes-slimness grows arbitrarily, since in general:
-
- enclosing-ball-slimness ⋅ enclosed-ball-slimness = two-balls-slimness
- enclosing-cube-slimness ⋅ enclosed-cube-slimness = two-cubes-slimness
Since all slimness factor are at least 1, it follows that if an object o is R-fat according to the two-balls/cubes definition, it is also R-fat according to the enclosing-ball/cube and enclosed-ball/cube definitions (but the opposite is not true, as exemplified above).
1.2. Balls vs. Cubes
The volume of a d-dimensional ball of radius r is: [math]\displaystyle{ V_d\cdot r^d }[/math], where Vd is a dimension-dependent constant:
- [math]\displaystyle{ V_d = \frac{\pi^{d/2}}{\Gamma(\frac{d}{2} + 1)} }[/math]
A d-dimensional cube with side-length 2a has volume (2a)d. It is enclosed in a d-dimensional ball with radius a√d whose volume is Vd(a√d)d. Hence for every d-dimensional object:
-
- enclosing-ball-slimness ≤ enclosing-cube-slimness ⋅ [math]\displaystyle{ {V_d}^{1/d}\cdot {\sqrt d} / 2 }[/math].
For even dimensions (d=2k), the factor simplifies to: [math]\displaystyle{ \sqrt{0.5 \pi k} / {{(k!)}^{1/2k}} }[/math]. In particular, for two-dimensional shapes V2=π and the factor is: √(0.5 π)≈1.25, so:
-
- enclosing-disk-slimness ≤ enclosing-square-slimness ⋅ 1.25
From similar considerations:
-
- enclosed-cube-slimness ≤ enclosed-ball-slimness ⋅ [math]\displaystyle{ {V_d}^{1/d}\cdot {\sqrt d} / 2 }[/math]
- enclosed-square-slimness ≤ enclosed-disk-slimness ⋅ 1.25
A d-dimensional ball with radius a is enclosed in a d-dimensional cube with side-length 2a. Hence for every d-dimensional object:
-
- enclosing-cube-slimness ≤ enclosing-ball-slimness ⋅ [math]\displaystyle{ 2 / {V_d}^{1/d} }[/math]
For even dimensions (d=2k), the factor simplifies to: [math]\displaystyle{ 2 / {(k!)}^{1/2k} / {\sqrt{\pi}} }[/math]. In particular, for two-dimensional shapes the factor is: 2/√π≈1.13, so:
-
- enclosing-square-slimness ≤ enclosing-disk-slimness ⋅ 1.13
From similar considerations:
-
- enclosed-ball-slimness ≤ enclosed-cube-slimness ⋅ [math]\displaystyle{ 2 / {V_d}^{1/d} }[/math]
- enclosed-disk-slimness ≤ enclosed-square-slimness ⋅ 1.13
Multiplying the above relations gives the following simple relations:
-
- two-balls-slimness ≤ two-cubes-slimness ⋅ √d
- two-cubes-slimness ≤ two-balls-slimness ⋅ √d
Thus, an R-fat object according to the either the two-balls or the two-cubes definition is at most R√d-fat according to the alternative definition.
2. Local Fatness
The above definitions are all global in the sense that they don't care about small thin areas that are part of a large fat object.
For example, consider a lollipop with a candy in the shape of a 1×1 square and a stick in the shape of a 1×(1/b) rectangle (with b>1>(1/b)). As b increases, the area of the enclosing cube (=4) and the area of the enclosed cube (=1) remain constant, while the total area of the shape changes only slightly (=1+1/b). Thus all three slimness factors are bounded: enclosing-cube-slimness≤2, enclosed-cube-slimness≤2, two-cube-slimness=2. Thus by all definitions the lollipop is 2-fat. However, the stick-part of the lollipop obviously becomes thinner and thinner.
In some applications, such thin parts are unacceptable, so local fatness, based on a local slimness factor, may be more appropriate. For every global slimness factor, it is possible to define a local version. For example, for the enclosing-ball-slimness, it is possible to define the local-enclosing-ball slimness factor of an object o by considering the set B of all balls whose center is inside o and whose boundary intersects the boundary of o (i.e. not entirely containing o). The local-enclosing-ball-slimness factor is defined as:[3][4]
- [math]\displaystyle{ \frac{1}{2}\cdot \sup_{b \in B}\left(\frac{\text{volume of} \ B}{\text{volume of} \ B\cap o}\right)^{1/d} }[/math]
The 1/2 is a normalization factor that makes the local-enclosing-ball-slimness of a ball equal to 1. The local-enclosing-ball-slimness of the lollipop-shape described above is dominated by the 1×(1/b) stick, and it goes to ∞ as b grows. Thus by the local definition the above lollipop is not 2-fat.
2.1. Global vs. Local Definitions
Local-fatness implies global-fatness. Here is a proof sketch for fatness based on enclosing balls. By definition, the volume of the smallest enclosing ball is ≤ the volume of any other enclosing ball. In particular, it is ≤ the volume of any enclosing ball whose center is inside o and whose boundary touches the boundary of o. But every such enclosing ball is in the set B considered by the definition of local-enclosing-ball slimness. Hence:
-
- enclosing-ball-slimnessd =
- = volume(smallest-enclosing-ball)/volume(o)
- ≤ volume(enclosing-ball-b-in-B)/volume(o)
- = volume(enclosing-ball-b-in-B)/volume(b ∩ o)
- ≤ (2 local-enclosing-ball-slimness)d
Hence:
-
- enclosing-ball-slimness ≤ 2⋅local-enclosing-ball-slimness
For a convex body, the opposite is also true: local-fatness implies global-fatness. The proof[3] is based on the following lemma. Let o be a convex object. Let P be a point in o. Let b and B be two balls centered at P such that b is smaller than B. Then o intersects a larger portion of b than of B, i.e.:
-
- [math]\displaystyle{ \frac{\text{volume} \ (b \cap o)}{\text{volume} \ (b)} \geq \frac{\text{volume} \ (B \cap o)}{\text{volume} \ (B)} }[/math]
Proof sketch: standing at the point P, we can look at different angles θ and measure the distance to the boundary of o. Because o is convex, this distance is a function, say r(θ). We can calculate the left-hand side of the inequality by integrating the following function (multiplied by some determinant function) over all angles:
-
- [math]\displaystyle{ f(\theta) = \min{(\frac{r(\theta)}{\text{radius} \ (b)},1)} }[/math]
Similarly we can calculate the right-hand side of the inequality by integrating the following function:
-
- [math]\displaystyle{ F(\theta) = \min{(\frac{r(\theta)}{\text{radius} \ (B)},1)} }[/math]
By checking all 3 possible cases, it is possible to show that always [math]\displaystyle{ f(\theta)\geq F(\theta) }[/math]. Thus the integral of f is at least the integral of F, and the lemma follows.
The definition of local-enclosing-ball slimness considers all balls that are centered in a point in o and intersect the boundary of o. However, when o is convex, the above lemma allows us to consider, for each point in o, only balls that are maximal in size, i.e., only balls that entirely contain o (and whose boundary intersects the boundary of o). For every such ball b:
-
- [math]\displaystyle{ \text{volume} \ (b)\leq C_d\cdot \text{diameter} \ (o)^d }[/math]
where [math]\displaystyle{ C_d }[/math] is some dimension-dependent constant.
The diameter of o is at most the diameter of the smallest ball enclosing o, and the volume of that ball is: [math]\displaystyle{ C_d\cdot(\text{diameter(smallest ball enclosing} \ o)/2)^d }[/math]. Combining all inequalities gives that for every convex object:
-
- local-enclosing-ball-slimness ≤ enclosing-ball-slimness
For non-convex objects, this inequality of course doesn't hold, as exemplified by the lollipop above.
3. Examples
The following table shows the slimness factor of various shapes based on the different definitions. The two columns of the local definitions are filled with "*" when the shape is convex (in this case, the value of the local slimness equals the value of the corresponding global slimness):
| Shape | two-balls | two-cubes | enclosing-ball | enclosing-cube | enclosed-ball | enclosed-cube | local-enclosing-ball | local-enclosing-cube |
|---|---|---|---|---|---|---|---|---|
| square | √2 | 1 | √(π/2)≈1.25 | 1 | √(4/π) ≈ 1.13 | 1 | * | * |
| b×a rectangle with b>a | √(1+b^2/a^2) | b/a | 0.5√π(a/b+b/a)[3] | √(b/a) | 2√(b/aπ) | √(b/a) | * | * |
| disk | 1 | √2 | 1 | √(4/π)≈1.13 | 1 | √(π/2)≈1.25 | * | * |
| ellipse with radii b>a | b/a | >b/a | √(b/a) | >√(b/2πa) | √(b/a) | >√(πb/a) | * | * |
| semi-ellipse with radii b>a, halved in parallel to b | 2b/a | >2b/a | √(2b/a) | >√(4b/πa) | √(2b/a) | >√(2πb/a) | * | * |
| semidisk | 2 | √5 | √2 | √(8/π)≈1.6 | √2 | √(5π/8)≈1.4 | * | * |
| equilateral triangle | 1+2/√3≈2.15 | √(π/√3)≈1.35 | √(4/√3)≈1.52 | √√3/2+1/√√3≈1.42 | * | * | ||
| isosceles right-angled triangle | 1/(√2-1)≈2.4 | 2 | √2 | √2 | * | * | ||
| 'lollipop' made of unit square and b×a stick, b>1>a | b+1 | √((b+1)^2/(ab+1)) | √(ab+1) | √(b/a) |
4. Fatness of a Triangle
Slimness is invariant to scale, so the slimness factor of a triangle (as of any other polygon) can be presented as a function of its angles only. The three ball-based slimness factors can be calculated using well-known trigonometric identities.
4.1. Enclosed-Ball Slimness
The largest circle contained in a triangle is called its incircle. It is known that:
- [math]\displaystyle{ \Delta = r^2\cdot(\cot \frac{\angle A}{2} + \cot \frac{\angle B}{2} + \cot \frac{\angle C}{2}) }[/math]
where Δ is the area of a triangle and r is the radius of the incircle. Hence, the enclosed-ball slimness of a triangle is:
- [math]\displaystyle{ \sqrt{ \frac{\cot \frac{\angle A}{2} + \cot \frac{\angle B}{2} + \cot \frac{\angle C}{2}}{\pi} } }[/math]
4.2. Enclosing-Ball Slimness
The smallest containing circle for an acute triangle is its circumcircle, while for an obtuse triangle it is the circle having the triangle's longest side as a diameter.[5]
It is known that:
- [math]\displaystyle{ \Delta = R^2 \cdot 2 \sin A \sin B \sin C }[/math]
where again Δ is the area of a triangle and R is the radius of the circumcircle. Hence, for an acute triangle, the enclosing-ball slimness factor is:
- [math]\displaystyle{ \sqrt{\frac{\pi}{2 \sin A \sin B \sin C}} }[/math]
It is also known that:
- [math]\displaystyle{ \Delta = \frac{c^{2}}{2(\cot \angle{A} + \cot \angle{B})} = \frac{c^{2} (\sin \angle{A})(\sin \angle{B})}{2\sin(\angle{A} + \angle{B})} }[/math]
where c is any side of the triangle and A,B are the adjacent angles. Hence, for an obtuse triangle with acute angles A and B (and longest side c), the enclosing-ball slimness factor is:
- [math]\displaystyle{ \sqrt{\frac{\pi\cdot(\cot \angle{A} + \cot \angle{B})}{2}} = \sqrt{\frac{\pi\cdot\sin(\angle{A} + \angle{B})}{2 (\sin \angle{A}) (\sin \angle{B})}} }[/math]
Note that in a right triangle, [math]\displaystyle{ \sin{\angle{C}}=\sin{\angle{A}+\angle{B}}=1 }[/math], so the two expressions coincide.
4.3. Two-Balls Slimness
The inradius r and the circumradius R are connected via a couple of formulae which provide two alternative expressions for the two-balls slimness of an acute triangle:[6]
- [math]\displaystyle{ \frac{R}{r} = \frac{1}{4 \sin(\frac{\angle{A}}{2}) \sin(\frac{\angle{B}}{2}) \sin(\frac{\angle{C}} {2})} = \frac{1}{\cos \angle{A} + \cos \angle{B} + \cos \angle{C} - 1} }[/math]
For an obtuse triangle, c/2 should be used instead of R. By the Law of sines:
- [math]\displaystyle{ \frac{c}{2} = R \sin{\angle{C}} }[/math]
Hence the slimness factor of an obtuse triangle with obtuse angle C is:
- [math]\displaystyle{ \frac{c/2}{r} = \frac{\sin{\angle{C}}}{4 \sin(\frac{\angle{A}}{2}) \sin(\frac{\angle{B}}{2}) \sin(\frac{\angle{C}} {2})} = \frac{\sin{\angle{C}}}{\cos \angle{A} + \cos \angle{B} + \cos \angle{C} - 1} }[/math]
Note that in a right triangle, [math]\displaystyle{ \sin{\angle{C}}=1 }[/math], so the two expressions coincide.
The two expressions can be combined in the following way to get a single expression for the two-balls slimness of any triangle with smaller angles A and B:
- [math]\displaystyle{ \frac{\sin{\max(\angle{A},\angle{B},\angle{C},\pi/2)}}{4 \sin(\frac{\angle{A}}{2}) \sin(\frac{\angle{B}}{2}) \sin(\frac{\pi-\angle{A}-\angle{B}} {2})} = \frac{\sin{\max(\angle{A},\angle{B},\angle{C},\pi/2)}}{\cos \angle{A} + \cos \angle{B} - \cos (\angle{A}+\angle{B}) - 1} }[/math]
To get a feeling of the rate of change in fatness, consider what this formula gives for an isosceles triangle with head angle θ when θ is small:
- [math]\displaystyle{ \frac{\sin{\max(\theta,\pi/2)}}{4 \sin^2(\frac{\pi-\theta}{4}) \sin(\frac{\theta}{2})} \approx \frac{1}{4 {\sqrt{1/2}}^2 \theta/2}=\frac{1}{\theta} }[/math]
The following graphs show the 2-balls slimness factor of a triangle:
- Slimness of a general triangle when one angle (a) is a constant parameter while the other angle (x) changes.
- Slimness of an isosceles triangle as a function of its head angle (x).
5. Fatness of Circles, Ellipses and Their Parts
The ball-based slimness of a circle is of course 1 - the smallest possible value.
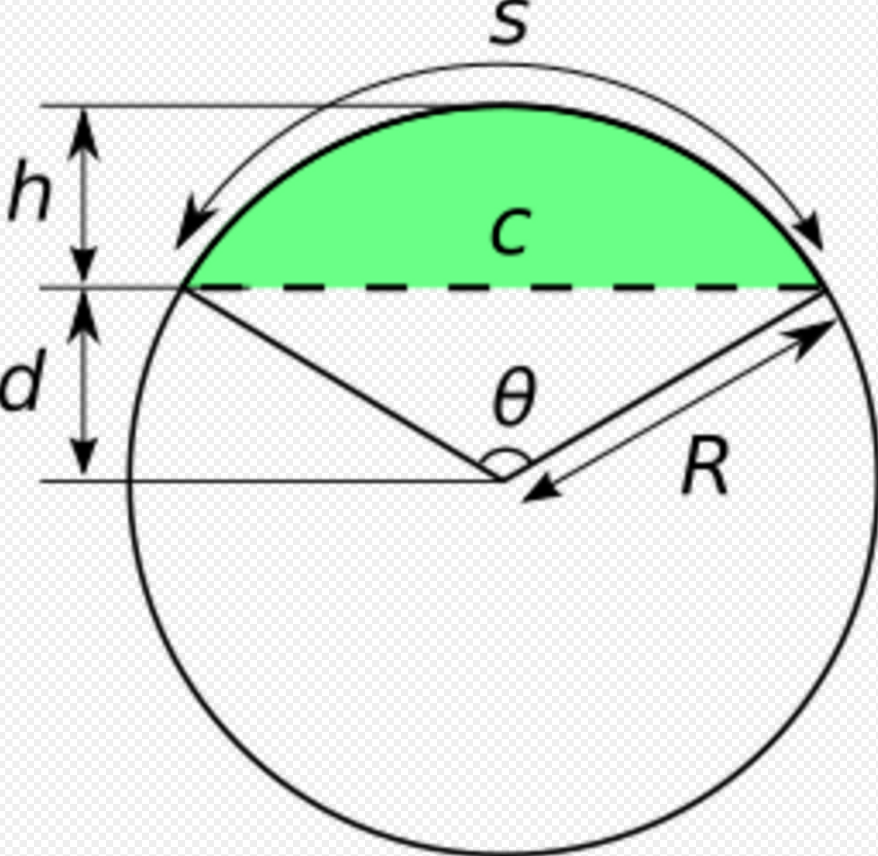
For a circular segment with central angle θ, the circumcircle diameter is the length of the chord and the incircle diameter is the height of the segment, so the two-balls slimness (and its approximation when θ is small) is:
- [math]\displaystyle{ \frac{\text{length of chord}}{\text{height of segment}}=\frac{2R\sin\frac{\theta}{2}}{R\left(1-\cos\frac{\theta}{2}\right)}=\frac{2\sin\frac{\theta}{2}}{\left(1-\cos\frac{\theta}{2}\right)} \approx \frac{\theta}{\theta^2/8} = \frac{8}{\theta} }[/math]
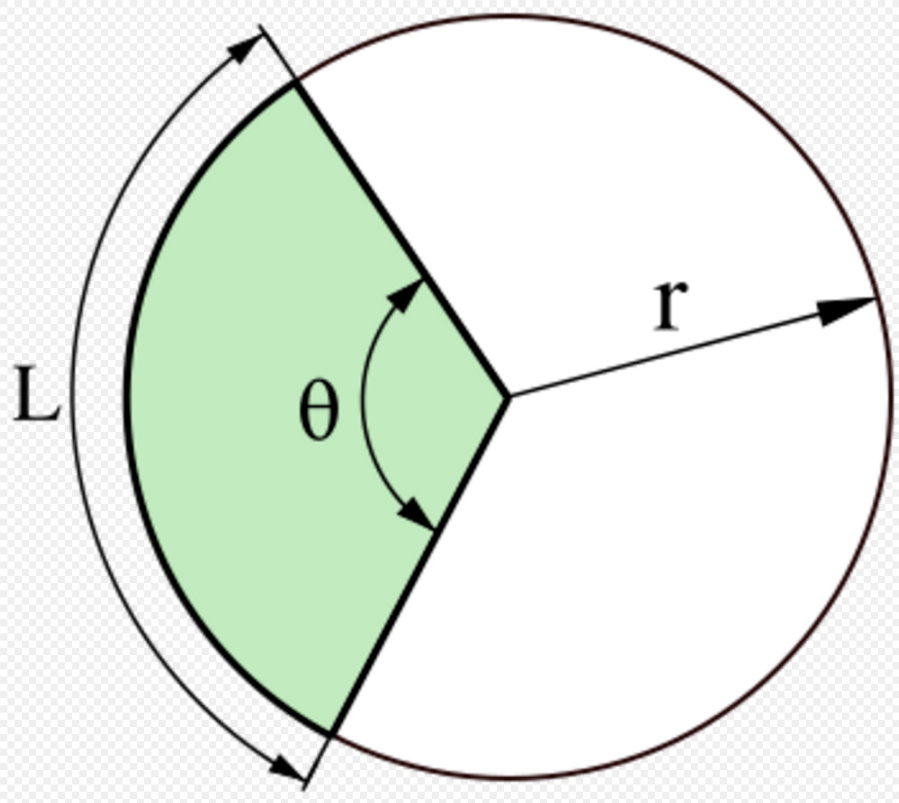
For a circular sector with central angle θ (when θ is small), the circumcircle diameter is the radius of the circle and the incircle diameter is the chord length, so the two-balls slimness is:
- [math]\displaystyle{ \frac{\text{radius of circle}}{\text{length of chord}}=\frac{R}{2R\sin\frac{\theta}{2}}=\frac{1}{2\sin\frac{\theta}{2}} \approx \frac{1}{2 \theta / 2} = \frac{1}{\theta} }[/math]
For an ellipse, the slimness factors are different in different locations. For example, consider an ellipse with short axis a and long axis b. the length of a chord ranges between [math]\displaystyle{ 2a\sin\frac{\theta}{2} }[/math] at the narrow side of the ellipse and [math]\displaystyle{ 2b\sin\frac{\theta}{2} }[/math] at its wide side; similarly, the height of the segment ranges between [math]\displaystyle{ b\left(1-\cos\frac{\theta}{2}\right) }[/math] at the narrow side and [math]\displaystyle{ a\left(1-\cos\frac{\theta}{2}\right) }[/math] at its wide side. So the two-balls slimness ranges between:
- [math]\displaystyle{ \frac{2a\sin\frac{\theta}{2}}{b\left(1-\cos\frac{\theta}{2}\right)} \approx \frac{8a}{b\theta} }[/math]
and:
- [math]\displaystyle{ \frac{2b\sin\frac{\theta}{2}}{a\left(1-\cos\frac{\theta}{2}\right)} \approx \frac{8b}{a\theta} }[/math]
In general, when the secant starts at angle Θ the slimness factor can be approximated by:[7]
- [math]\displaystyle{ \frac{2\sin\frac{\theta}{2}}{\left(1-\cos\frac{\theta}{2}\right)} }[/math] [math]\displaystyle{ \left(\frac{b}{a}\cos^2(\Theta+\frac{\theta}{2}) + \frac{a}{b}\sin^2(\Theta+\frac{\theta}{2})\right) }[/math]
6. Fatness of a Convex Polygon
A convex polygon is called r-separated if the angle between each pair of edges (not necessarily adjacent) is at least r.
Lemma: The enclosing-ball-slimness of an r-separated convex polygon is at most [math]\displaystyle{ O(1/r) }[/math].[8]:7-8
A convex polygon is called k,r-separated if:
- It does not have parallel edges, except maybe two horizontal and two vertical.
- Each non-axis-parallel edge makes an angle of at least r with any other edge, and with the x and y axes.
- If there are two horizontal edges, then diameter/height is at most k.
- If there are two vertical edges, then diameter/width is at most k.
Lemma: The enclosing-ball-slimness of a k,r-separated convex polygon is at most [math]\displaystyle{ O(\max(k,1/r)) }[/math].[9] improve the upper bound to [math]\displaystyle{ O(d) }[/math].
7. Counting Fat Objects
If an object o has diameter 2a, then every ball enclosing o must have radius at least a and volume at least Vdad. Hence, by definition of enclosing-ball-fatness, the volume of an R-fat object with diameter 2a must be at least: Vdad/Rd. Hence:
- Lemma 1: Let R≥1 and C≥0 be two constants. Consider a collection of non-overlapping d-dimensional objects that are all globally R-fat (i.e. with enclosing-ball-slimness ≤ R). The number of such objects of diameter at least 2a, contained in a ball of radius C⋅a, is at most:
- [math]\displaystyle{ V_d\cdot (C a)^d / (V_d \cdot a^d / R^d) = (R C)^d }[/math]
For example (taking d=2, R=1 and C=3): The number of non-overlapping disks with radius at least 1 contained in a circle of radius 3 is at most 32=9. (Actually, it is at most 7).
If we consider local-fatness instead of global-fatness, we can get a stronger lemma:[3]
- Lemma 2: Let R≥1 and C≥0 be two constants. Consider a collection of non-overlapping d-dimensional objects that are all locally R-fat (i.e. with local-enclosing-ball-slimness ≤ R). Let o be a single object in that collection with diameter 2a. Then the number of objects in the collection with diameter larger than 2a that lie within distance 2C⋅a from object o is at most:
- [math]\displaystyle{ (4 R \cdot (C+1))^d }[/math]
For example (taking d=2, R=1 and C=0): the number of non-overlapping disks with radius larger than 1 that touch a given unit disk is at most 42=16 (this is not a tight bound since in this case it is easy to prove an upper bound of 5).
8. Generalizations
The following generalization of fatness were studied by [2] for 2-dimensional objects.
A triangle ∆ is a (β, δ)-triangle of a planar object o (0<β≤π/3, 0<δ< 1), if ∆ ⊆ o, each of the angles of ∆ is at least β, and the length of each of its edges is at least δ·diameter(o). An object o in the plane is (β,δ)-covered if for each point P ∈ o there exists a (β, δ)-triangle ∆ of o that contains P.
For convex objects, the two definitions are equivalent, in the sense that if o is α-fat, for some constant α, then it is also (β,δ)-covered, for appropriate constants β and δ, and vice versa. However, for non-convex objects the definition of being fat is more general than the definition of being (β, δ)-covered.[2]
9. Applications
Fat objects are used in various problems, for example:
- Motion planning - planning a path for a robot moving amidst obstacles becomes easier when the obstacles are fat objects.[3]
- Fair cake-cutting - dividing a cake becomes more difficult when the pieces have to be fat objects. This requirement is common, for example, when the "cake" to be divided is a land-estate.[10]
- More applications can be found in the references below.
References
- Katz, M. J. (1997). "3-D vertical ray shooting and 2-D point enclosure, range searching, and arc shooting amidst convex fat objects". Computational Geometry 8 (6): 299–316. doi:10.1016/s0925-7721(96)00027-2. , Agarwal, P. K.; Katz, M. J.; Sharir, M. (1995). "Computing depth orders for fat objects and related problems". Computational Geometry 5 (4): 187. doi:10.1016/0925-7721(95)00005-8. https://dx.doi.org/10.1016%2Fs0925-7721%2896%2900027-2
- Efrat, A.; Katz, M. J.; Nielsen, F.; Sharir, M. (2000). "Dynamic data structures for fat objects and their applications". Computational Geometry 15 (4): 215. doi:10.1016/s0925-7721(99)00059-0. https://dx.doi.org/10.1016%2Fs0925-7721%2899%2900059-0
- Van Der Stappen, A. F.; Halperin, D.; Overmars, M. H. (1993). "The complexity of the free space for a robot moving amidst fat obstacles". Computational Geometry 3 (6): 353. doi:10.1016/0925-7721(93)90007-s. https://dx.doi.org/10.1016%2F0925-7721%2893%2990007-s
- Berg, M.; Groot, M.; Overmars, M. (1994). "New results on binary space partitions in the plane (extended abstract)". Algorithm Theory — SWAT '94. Lecture Notes in Computer Science. 824. pp. 61. doi:10.1007/3-540-58218-5_6. ISBN 978-3-540-58218-2. , Van Der Stappen, A. F.; Overmars, M. H. (1994). "Motion planning amidst fat obstacles (extended abstract)". Proceedings of the tenth annual symposium on Computational geometry - SCG '94. pp. 31. doi:10.1145/177424.177453. ISBN 978-0897916486. , Overmars, M. H. (1992). "Point location in fat subdivisions". Information Processing Letters 44 (5): 261–265. doi:10.1016/0020-0190(92)90211-d. , Overmars, M. H.; Van Der Stappen, F. A. (1996). "Range Searching and Point Location among Fat Objects". Journal of Algorithms 21 (3): 629. doi:10.1006/jagm.1996.0063. https://dx.doi.org/10.1007%2F3-540-58218-5_6
- "How fat is a triangle?". https://math.stackexchange.com/q/915187. Retrieved 28 September 2014.
- Weisstein, Eric W. "Inradius". http://mathworld.wolfram.com/Inradius.html. Retrieved 28 September 2014.
- See graph at: https://www.desmos.com/calculator/fhfqju02sn
- Mark de Berg; Onak, Krzysztof; Sidiropoulos, Anastasios (2010). "Fat Polygonal Partitions with Applications to Visualization and Embeddings". Journal of Computational Geometry Vol 4. doi:10.20382/jocg.v4i1a9. https://dx.doi.org/10.20382%2Fjocg.v4i1a9
- De Berg, Mark; Speckmann, Bettina; Van Der Weele, Vincent (2014). "Treemaps with bounded aspect ratio". Computational Geometry 47 (6): 683. doi:10.1016/j.comgeo.2013.12.008. . Conference version: "Convex Treemaps with Bounded Aspect Ratio". EuroCG. 2011. http://alexandria.tue.nl/openaccess/Metis253577.pdf.
- Segal-Halevi, Erel; Nitzan, Shmuel; Hassidim, Avinatan; Aumann, Yonatan (2017). "Fair and square: Cake-cutting in two dimensions". Journal of Mathematical Economics 70: 1–28. doi:10.1016/j.jmateco.2017.01.007. https://dx.doi.org/10.1016%2Fj.jmateco.2017.01.007




