
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Sirius Huang | -- | 1249 | 2022-11-28 01:37:46 |
Video Upload Options
In geometry, the Petr–Douglas–Neumann theorem (or the PDN-theorem) is a result concerning arbitrary planar polygons. The theorem asserts that a certain procedure when applied to an arbitrary polygon always yields a regular polygon having the same number of sides as the initial polygon. The theorem was first published by Karel Petr (1868–1950) of Prague in 1908. The theorem was independently rediscovered by Jesse Douglas (1897–1965) in 1940 and also by B H Neumann (1909–2002) in 1941. The naming of the theorem as Petr–Douglas–Neumann theorem, or as the PDN-theorem for short, is due to Stephen B Gray. This theorem has also been called Douglas's theorem, the Douglas–Neumann theorem, the Napoleon–Douglas–Neumann theorem and Petr's theorem. The PDN-theorem is a generalisation of the Napoleon's theorem which is concerned about arbitrary triangles and of the van Aubel's theorem which is related to arbitrary quadrilaterals.
1. Statement of the Theorem
The Petr–Douglas–Neumann theorem asserts the following.[1][2]
- If isosceles triangles with apex angles 2kπ/n are erected on the sides of an arbitrary n-gon A0, and if this process is repeated with the n-gon formed by the free apices of the triangles, but with a different value of k, and so on until all values 1 ≤ k ≤ n − 2 have been used (in arbitrary order), then a regular n-gon An−2 is formed whose centroid coincides with the centroid of A0.
2. Specialisation to Triangles
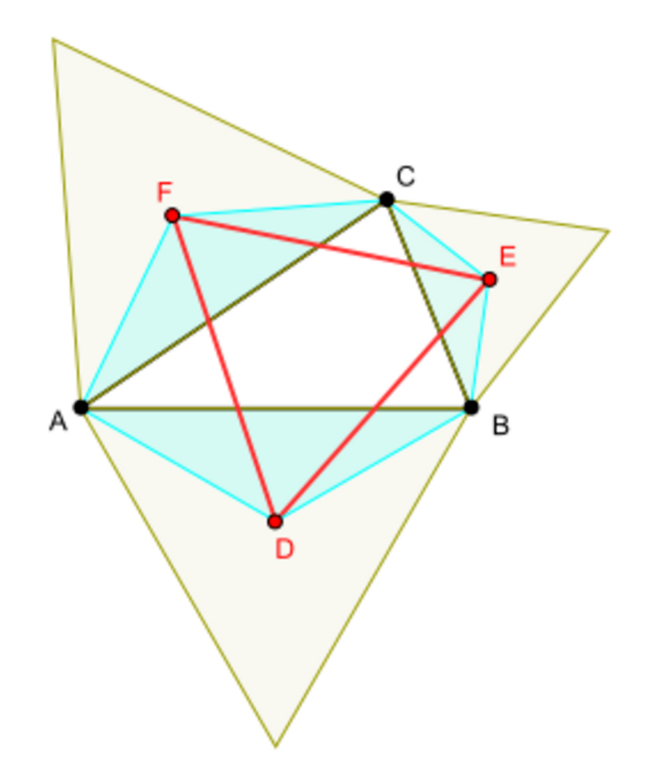
In the case of triangles, the value of n is 3 and that of n − 2 is 1. Hence there is only one possible value for k, namely 1. The specialisation of the theorem to triangles asserts that the triangle A1 is a regular 3-gon, that is, an equilateral triangle.
A1 is formed by the apices of the isosceles triangles with apex angle 2π/3 erected over the sides of the triangle A0. The vertices of A1 are the centers of equilateral triangles erected over the sides of triangle A0. Thus the specialisation of the PDN theorem to a triangle can be formulated as follows:
- If equilateral triangles are erected over the sides of any triangle, then the triangle formed by the centers of the three equilateral triangles is equilateral.
The last statement is the assertion of the Napoleon's theorem.
3. Specialisation to Quadrilaterals
In the case of quadrilaterals, the value of n is 4 and that of n − 2 is 2. There are two possible values for k, namely 1 and 2, and so two possible apex angles, namely:
- (2×1×π)/4 = π/2 = 90° ( corresponding to k = 1 )
- (2×2×π)/4 = π = 180° ( corresponding to k = 2 ).
According to the PDN-theorem the quadrilateral A2 is a regular 4-gon, that is, a square. The two-stage process yielding the square A2 can be carried out in two different ways. (The apex Z of an isosceles triangle with apex angle π erected over a line segment XY is the midpoint of the line segment XY.)
3.1. Construct A1 using Apex Angle π/2 and then A2 with Apex Angle π
In this case the vertices of A1 are the free apices of isosceles triangles with apex angles π/2 erected over the sides of the quadrilateral A0. The vertices of the quadrilateral A2 are the midpoints of the sides of the quadrilateral A1. By the PDN theorem, A2 is a square.
The vertices of the quadrilateral A1 are the centers of squares erected over the sides of the quadrilateral A0. The assertion that quadrilateral A2 is a square is equivalent to the assertion that the diagonals of A1 are equal and perpendicular to each other. The latter assertion is the content of van Aubel's theorem.
Thus van Aubel's theorem is a special case of the PDN-theorem.
3.2. Construct A1 using Apex Angle π and then A2 with Apex Angle π/2
In this case the vertices of A1 are the midpoints of the sides of the quadrilateral A0 and those of A2 are the apices of the triangles with apex angles π/2 erected over the sides of A1. The PDN-theorem asserts that A2 is a square in this case also.
3.3. Images Illustrating Application of the Theorem to Quadrilaterals
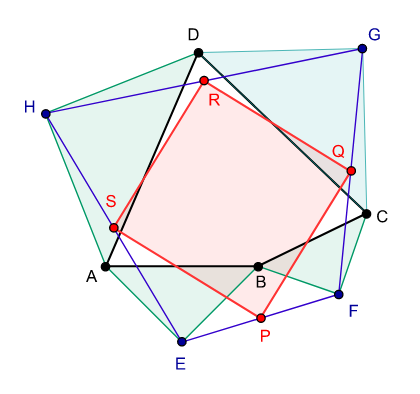 |
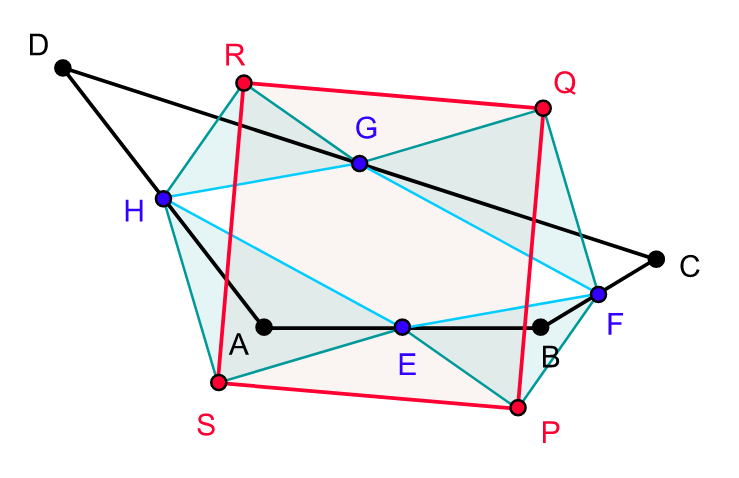 |
| Petr–Douglas–Neumann theorem as applied to a quadrilateral A0 = ABCD. A1 = EFGH is constructed using apex angle π/2 and A2 = PQRS with apex angle π. |
Petr–Douglas–Neumann theorem as applied to a quadrilateral A0 = ABCD. A1 = EFGH is constructed using apex angle π and A2 = PQRS with apex angle π/2. |
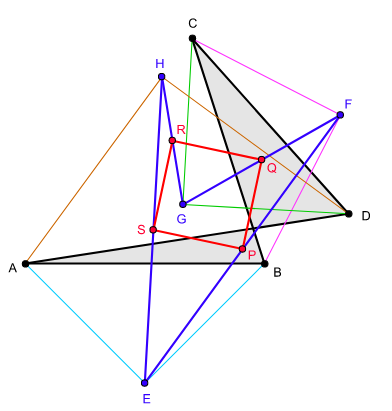 |
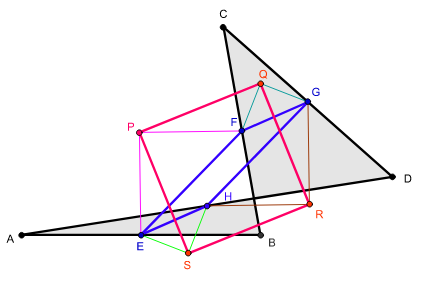 |
| Petr–Douglas–Neumann theorem as applied to a self-intersecting quadrilateral A0 = ABCD. A1 = EFGH is constructed using apex angle π/2 and A2 = PQRS with apex angle π. |
Petr–Douglas–Neumann theorem as applied to a self-intersecting quadrilateral A0 = ABCD. A1 = EFGH is constructed using apex angle π and A2 = PQRS with apex angle π/2. |
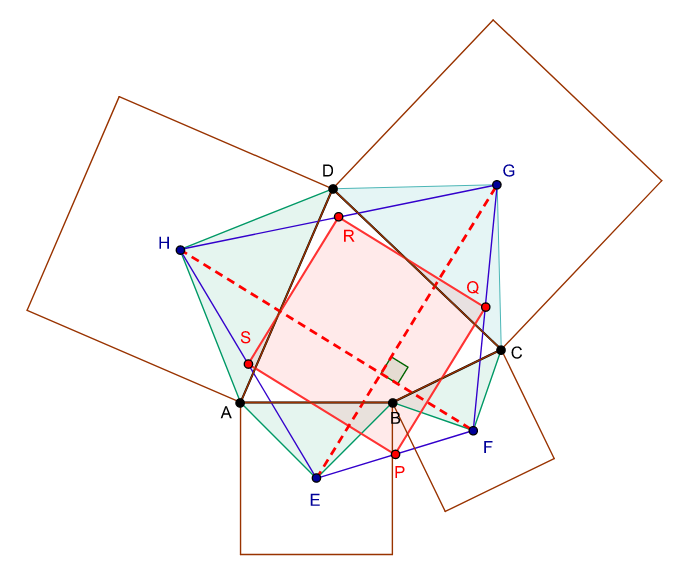 |
| Diagram illustrating the fact that van Aubel's theorem is a special case of Petr–Douglas–Neumann theorem. https://handwiki.org/wiki/index.php?curid=2079397 |
4. Specialisation to Pentagons
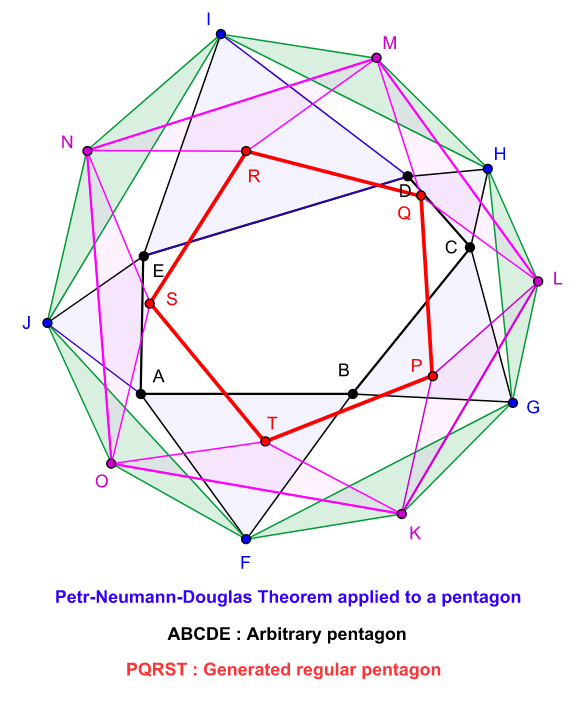
In the case of pentagons, we have n = 5 and n − 2 = 3. So there are three possible values for k, namely 1, 2 and 3, and hence three possible apex angles for isosceles triangles:
- (2×1×π)/5 = 2π/5 = 72°
- (2×2×π)/5 = 4π/5 = 144°
- (2×3×π)/5 = 6π/5 = 216°
According to the PDN-theorem, A3 is a regular pentagon. The three-stage process leading to the construction of the regular pentagon A3 can be performed in six different ways depending on the order in which the apex angles are selected for the construction of the isosceles triangles.
| Serial number |
Apex angle in the construction of A1 |
Apex angle in the construction of A2 |
Apex angle in the construction of A3 |
|---|---|---|---|
| 1 | 72° | 144° | 216° |
| 2 | 72° | 216° | 144° |
| 3 | 144° | 72° | 216° |
| 4 | 144° | 216° | 72° |
| 5 | 216° | 72° | 144° |
| 6 | 216° | 144° | 72° |
5. Proof of the Theorem
The theorem can be proved using some elementary concepts from linear algebra.[3][4]
The proof begins by encoding an n-gon by a list complex numbers representing the vertices of the n-gon. This list can be thought of as a vector in the n-dimensional complex linear space Cn. Take an n-gon A and let it be represented by the complex vector
- A = ( a1, a2, ... , an ).
Let the polygon B be formed by the free vertices of similar triangles built on the sides of A and let it be represented by the complex vector
- B = ( b1, b2, ... , bn ).
Then we have
- α( ar − br ) = ar+1 − br, where α = exp( i θ ) for some θ (here i is the square root of −1).
This yields the following expression to compute the br ' s:
- br = (1−α)−1 ( ar+1 − αar ).
In terms of the linear operator S : Cn → Cn that cyclically permutes the coordinates one place, we have
- B = (1−α)−1( S − αI )A, where I is the identity matrix.
This means that the polygon An−2 that we need to show is regular is obtained from A0 by applying the composition of the following operators:
- ( 1 − ωk )−1( S − ωk I ) for k = 1, 2, ... , n − 2, where ω = exp( 2πi/n ). (These commute because they are all polynomials in the same operator S.)
A polygon P = ( p1, p2, ..., pn ) is a regular n-gon if each side of P is obtained from the next by rotating through an angle of 2π/n, that is, if
- pr + 1 − pr = ω( pr + 2 − pr + 1 ).
This condition can be formulated in terms of S as follows:
- ( S − I )( I − ωS ) P = 0.
Or equivalently as
- ( S − I )( S − ωn − 1 I ) P = 0, since ωn = 1.
Petr–Douglas–Neumann theorem now follows from the following computations.
- ( S − I )( S − ωn − 1 I ) An − 2
- = ( S − I )( S − ωn − 1 I ) ( 1 − ω )−1 ( S − ω I ) ( 1 − ω2 )−1 ( S − ω2 I ) ... ( 1 − ωn − 2 )−1 ( S − ωn − 2 I ) A0
- = ( 1 − ω )−1( 1 − ω2 )−1 ... ( 1 − ωn − 2 )−1 ( S − I ) ( S − ω I ) ( S − ω2 I ) ... ( S − ωn − 1 I)A0
- = ( 1 − ω )−1( 1 − ω2 )−1 ... ( 1 − ωn − 2 )−1 ( Sn − I ) A0
- = 0, since Sn = I.
References
- Douglas, Jesse (1946). "On linear polygon transformations". Bulletin of the American Mathematical Society 46 (6): 551–561. doi:10.1090/s0002-9904-1940-07259-3. http://www.ams.org/journals/bull/1940-46-06/S0002-9904-1940-07259-3/S0002-9904-1940-07259-3.pdf. Retrieved 7 May 2012.
- "Petr–Neumann–Douglas Theorem.". From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/Petr-Neumann-DouglasTheorem.html. Retrieved 8 May 2012.
- Stephen B. Gray (2003). "Generalizing the Petr–Douglas–Neumann Theorem on n-gons". American Mathematical Monthly 110 (3): 210–227. doi:10.2307/3647935. http://www.experimentalmath.info/workshop2004/gray-article.pdf. Retrieved 8 May 2012.
- Omar Antolín Camarena. "The Petr–Neumann–Douglas theorem through linear algebra". http://www.matem.unam.mx/omar/notes/petr.html. Retrieved 10 Jan 2018.




