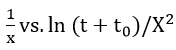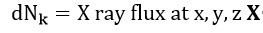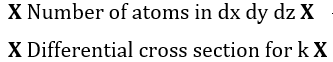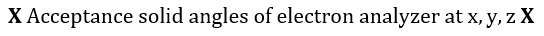| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | César Augusto Correia De Sequeira | + 6744 word(s) | 6744 | 2020-12-18 03:16:31 | | | |
| 2 | Lily Guo | -2 word(s) | 6742 | 2020-12-18 04:54:49 | | | | |
| 3 | Lily Guo | -6 word(s) | 6738 | 2020-12-18 05:09:21 | | | | |
| 4 | Lily Guo | Meta information modification | 6738 | 2020-12-18 10:15:08 | | | | |
| 5 | Lily Guo | + 17 word(s) | 6755 | 2020-12-21 03:51:54 | | |
Video Upload Options
The outstanding corrosion resistance of many metals and alloys results from the presence of a thin oxide-“passive”-film on the bare metal surface formed during its exposure to an oxidising environment. Once a film is formed, typically 1-3 nm thick, the reaction rate between the metallic material and the environment will be several orders of magnitude lower. The original theory of film formation goes back to Michael Faraday, who in the 19th century studied iron surfaces and found them “altered”. A review of the early days of passive film research has been written by Uhlig (1979). A general introduction to the theory of passivity has been published by Sato (1990), whereas the electronic properties of passive films on different materials have been reviewed by Schultze and Lohrengel (2000). The characterisation of the composition and structure of such thin films and the study of their interaction with corrosive environments requires a combination of sophisticated experimental techniques, namely electrochemical methods, XPS, ESCA, AES, SIMS, ISS, ARXPS, XANES, ICP-AES/MS, and others, which are leading to advanced progress over the past two decades.
1.Introduction
The passive state of a metal may be defined by the following: a metal is passive when the amount of metal consumed by a chemical or electrochemical reaction at a given time is significantly less under the conditions corresponding to a higher affinity of the reaction than under the conditions corresponding to a lower affinity[1], or a metal is in a state of improved corrosion resistance accounted for by inhibition of the anodic process[2].
As most of the conditions leading to spontaneous passivity are related to galvanic processes, electrochemical methods have been used extensively, and still prove powerful especially when used along with surface physics techniques, Both theoretically and practically, the most interesting aspect of the passivation phenomenon is the determination of the mechanism underlying the produced passivation, the search for the cause of passivation along with a fuller understanding of the surface changes resulting in active-passive transition. The theory and basic experimental techniques used to investigate the passivation phenomenon will be considered and reviewed in this entry.
2. Passivation Theory
Many theories of metal passivity have been presented in the literature. The major theories which have been developed are the oxide film theory and the adsorption theory of passivity [3][4][5][6][7][8][9][10][11][12][13]. The oxide film theory ascribes the state of improved corrosion resistance to the formation of a protective film on the metal substrate. Such a film is a new phase, even if it is as thin as a single monolayer. Proponents of this theory have different opinions about the potential at which the film forms, its thickness, the mechanism of formation and the cause of passivity. In the earlier theories it was postulated that passivation follows the formation of a primary layer of low conductivity of a porous character. The cur rent increases in the pores and, by polarization at a potential close to the Flade potential, a passive layer is formed. Thus, the essence of the passivation process is the change of the properties of the primary film at a certain potential. The passive film is free from pores and presents a barrier between the metal and the environment. It is electronically conductive and slowly corrodes in solution[14]. Historically, the main support of this theory has come from isolation of thin oxide films from passive iron. In 1927, Evans[15] isolated an oxide film from air exposed iron passivated in chromate solution by immersing the specimen in a saturated solution of iodine in 10 % KI. He examined the oxide peeled off and reported that the oxide responsible for passivity was Fe2O3. Electron diffraction[16] and ellipsometric studies[17] produce experimental evidence for the theory. De Gromoboy and Shreir[18] proposed in their experimental study of nickel in sulphuric acid that higher oxides may form directly from the metal.
This and many other similar hypotheses can be said to form the monolayer oxide theories. For example, Frankenthal[19] proposed that anodic current decreased due to blocking of the most active sites by film formation. This blocking influenced the kinetics of the anodic reaction. But whatever arguments may have been invoked leading to other conclusions, the oxide film theory continues to receive popular support in explaining the passivity of many metal and alloy systems. On the other hand, the adsorption theory holds that chemisorbed films displace the normally adsorbed water molecules and slow down the rate of anodic dissolution involving hydration of metal ions. This theory was supported by Langmuir[20] who showed oxygen adsorbed on tungsten to exhibit reduced chemical reactivity compared to oxygen in the oxide WO3. In 1946, Uhlig[21] proposed that an adsorbed oxygen film is the primary source of passivity. Such a film forms preferentially on the transition metals in accordance with their uncoupled d electrons interacting with oxygen to form a stable bond, combined with their high heats of sublimation favouring retention of metal atoms in their lattice in preference to their removal to form an oxide lattice. He proposed that a film of adsorbed oxygen atoms markedly decreases the exchange current density in the Tafel equation and hence increases anodic polarization in accordance with the requirements of passive behaviour[21]. For non-transition metals with filled d levels, such as copper or zinc, the heats of oxygen adsorption are expected to be lower, and the formation of oxides is less favourable. Such metals do not exhibit thin-film passivity.
Correlating millicoulombs with film thickness, it can be calculated that 0.5 mC/cm2 will correspond to a monolayer of O2- ions if each metal ion adsorbs one oxygen ion. If the adsorbed layer has a structure that contains both metal and oxygen ions, the resulting passivating film is several layers thick – that is, a thin oxide is more likely than an adsorbed multilayer of O2-.
In this respect, as pointed out by an increasing number of writers, the oxide film and adsorption theories do not contradict but rather supplement one another.
An alternative mechanism for passivity could be direct film formation, dissolution and precipitation and anodic deposition[22]. First, there is the direct reaction of the metal with the solution to form an adsorbed oxygen film, a com pact oxide film, or a protective solid state film on the metal surface. Second, the dissolution-precipitation process consisting of anodic metal dissolution and precipitation of dissolved metal ions can lead to a passivating oxide or insoluble salt film. The third process is a consecutive reaction of anodic metal dissolution followed by oxidation of dissolved metal ions to produce an anodic deposit oxide or salt film.
Armstrong[23] has suggested that investigations with a rotating disc electrode can be used to distinguish between chemisorption and dissolution. If dissolution-precipitation applies, the shape of the polarization curve must be influenced by a change in the speed at which the rotating disc electrode rotates and if chemisorption applies, the curve will not be influenced by the speed of rotation.
2.1. The logarithmic law for thin film
The rate equations which are most commonly encountered in describing passive film formation may be classified as logarithmic, parabolic and linear. They represent only limiting and ideal cases. Other rate equations may also be found to fit the rate data.
In 1939, Mott proposed a logarithmic model[24] to explain the limiting thickness behaviour of the growth kinetics of thin oxide films on metals. After this, much research work was accomplished on the growth of preformed films and on the latter stages of growth of newly formed ones. Logarithmic equations are generally divided into two categories: direct and inverse logarithmic relations.
2.1.1. Mott and Cabrera model
This model was proposed by Mott [24] and was extended by Cabrera and Mott[25]. The assumptions made in the model are as follows:
- Film growth is by migration of cations across the oxide film to the interface of film and solution, and the rate of oxidation is determined by the rate at which ions escape from the metal.
- Oxygen molecules dissociate on the oxide surface, giving rise to traps with an energy eV below the Fermi level of the metal, where V is the contact potential difference between the metal and the adsorbed oxygen layer.
- The penetration of ions through the film is assisted by the high electric field strength which is given as V/X, X being the film thickness.
- V is constant and is independent of film thickness.
- The activation energy W for the movement of a cation in the oxide drops to (W – 0.5 qaF), where q is the charge on the ion and a the jump distance.
The growth rate is thus of the form
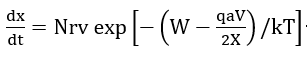
where N is the number of mobile ions per unit area surface, r is the molecular volume per cation, v is a phonon frequency and kT is the thermal energy. An approximate integration of equation (1) was carried out by parts and led to the inverse logarithmic law

where A and B are related to u, and which are defined in their paper. Thus, plot of 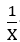
2.1.2. Ghez modified model
Ghez[26]] examined the integration of equation (1) and discussed several difficulties associated with the evaluation of parameters A and B. According to his calculations, the inverse logarithmic kinetic expression derived by Cabrera and Mott is not an asymptotic solution of equation (1). He obtained as a solution the expression
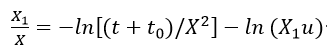
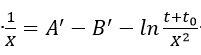
where A’ and B’ are constants and other parameters are defined as the same in the Mott-Cabrera model. Thus, a plot of
should yield a straight line with slope -(1 / X1) and intercept - (1/ X1) ln (X1u), from which the physical parameters of the theory u and X1 can be evaluated.
2.1.3. Sato and Cohen model
From their potentiostatic and galvanostatic study of iron in pH 8.4 borate buffer solution, Sato and Cohen[27] found that the rate of film growth could be expressed by the empirical equation
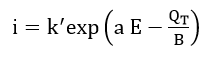
where QT is the film thickness, E is the potential and k', a and B are constants. In order to explain this relationship, they used the so-called “place-exchange” mechanism which was first proposed by Lanyon and Trapnell[28]. According to this model, an oxygen atom is adsorbed and exchanges places (possibly by rotation) with an underlying metal atom. A second oxygen atom is then adsorbed, and the two M-O pairs rotate simultaneously. This process repeats and, if all exchanges are simultaneous, then the activation energy should increase linearly with thickness. This model gives the expressions for the parameters in equation (5) as:
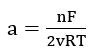
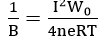
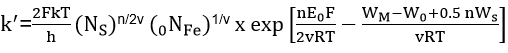
The meaning of the constants and parameters can be obtained from the original paper.
Later, Sato and Notoya[29] applied equation (5) to the potentiostatic case and integrated the equation to obtain the logarithmic law
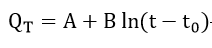
where A and B are constants and are functions of temperature. Sato and Cohen obtained the activation energy for a single place exchange as 3.5 kcal/mole for their system.
2.1.4. Fehlner and Mott model
Fehlner and Mott modified the Mott- Cabrera model to explain phenomena such as anion migration during oxide growth and the transition from the initial chemisorbed monolayer to a bulk, three dimensional oxide. The modifications include the place exchange mechanism and assumptions such as[30]:
- The film growth is due to the migration of anions.
- The rate determining step is the transfer of an anion from the solution into the film.
- The structure of film changes with thickness so that the potential drop across the film increases as the film thickens in such a way that the field remains constant.
- With these assumptions, the activation energy has the form W0 + µx where W0 and μ are constants dependent on film structure; therefore
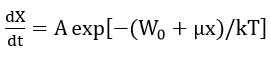
and
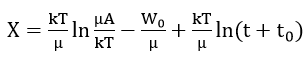
or
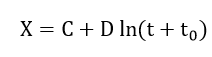
In addition to these four models for film growth on metal surfaces, there are several other logarithmic growth models. Some of the proposed mechanisms for film growth are non- linear ion diffusion in a large surface charge field due to space charge[31], variation of the boundary values of bulk concentration with film thickness[32][33], structure changes during growth[34] and deactivation of the surface with increasing thickness[35]. In order to derive a logarithmic growth law, it should be noted that any mechanism which involves a linear activation energy with film thickness could result in this relationship[36]. Studies at several laboratories[37][38][39][40][41][42][43][44] revealed that both cation and anion transport are responsible for film growth. All the models proposed above assumed either cation or anion transportation only.
2.2. The parabolic law for thick films
Several derivations of the parabolic law have been reported in the literature[37][38][45][46][47][48][49] [37,38,45-49], but for the most part, these derivations are based on Fick’s law for the diffusion of uncharged particles.
Wagner[37] developed parabolic equations to explain the phenomena of metal tarnishing in aggressive environments. He assumed that transport of neutral species was negligible compared to that of all the charged carriers migrating with Einstein-type mobilities under the combined influence of free energy gradients and electric field. Using these assumptions, he was able to transform the problem of parabolic scale growth on metals to one of diffusional transport in an electrochemical medium. In his general equations, Wagner used essentially an enhanced mobility defined as the reciprocal of 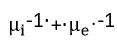
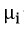
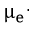
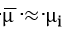

Assuming electrical neutrality for each point in the film, this equation reduces to the form
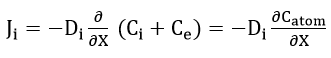
This is Wagner’s derivation for these conditions which is equivalent to Fick’s law for the diffusion of uncharged particles. A replacement of concentration by activities results in no essential change in the form of the equation. Conductivity measurements on Cu2O by Wagner and Grünwald[38] have shown that transport occurs by motion of positive holes and copper ion vacancies.
Cabrera and Mott[25] derived a parabolic law for thick films based on the assumption of equal electronic and ionic currents but neglected the coupling between the diffusion equations. In the case of an oxide which is an insulator and for which X >> X0, the rate is controlled by diffusion of ions and the equation can be expressed as

where
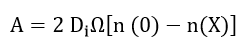
In case of a good conductor, the rate is controlled by diffusion of electrons and the parameter is expressed as

where De and Di are the diffusion coefficients of the electrons and ions, respectively. The volume of oxide per metal ion is Ω, n is the concentration of ions or electrons at the interface, X is the film thickness, and X0 is a parameter. Fromhold developed the parabolic law from the coupled diffusion equation. By assuming equal ionic and electronic diffusion currents with a thickness dependent surface charge he showed that the rate determining step is interpreted to be transport of the low mobility species in the presence of the electric field created by the high mobility species.
3. Electrochemical Methods
In general, the methods used to study passivity of metals are classified into two groups: electrochemical techniques which measure corrosion rate rapidly and non-electrochemical techniques which include a number of film analysis instruments such as ellipsometry, ESCA, AES, etc.
Historically, most of the early investigations on passivity have been carried out by electrochemical techniques. Electrochemical studies on the passivity of metals can be divided into two types – those concerned with the mechanism by which the passive state is attained, destroyed or modified and those concerned with the nature of this state. Very often, both aspects are determined simultaneously by the experimental methods used[50][51][52][53][54] [50-54].
Electrochemical techniques may be divided into three categories:
- techniques for studying passivity in the steady state
- techniques based on a large perturbation such as potentiostatic or galvanostatic transients or by completely forming or removing the passive state, or by a linear potential sweep (potentiodynamic techniques) at various sweep rates, and
- techniques involving a small perturbation of the state of the interface. These include modern AC techniques. Provided the amplitude of the voltage or current transient is small enough, the behaviour of the electrode under such a perturbation can be readily described in terms of its impedance.
Fundamentally, the electrochemical approach to passivity implies that the phenomenon remains essentially the same under chemical treatment to produce passivity, or by the application of an anodic current, noble potentials being associated with the passive state in both cases. Oxidizing agents, therefore, induce chemical passivity because their cathodic reduction current brings the rest potential into the passive range. This basic assumption is involved in any correlation between corrosion rate and electrochemical behaviour and it has been verified as shown by Kolotyrkin and Bune[40].
Polarization curves are mainly concerned with characterizing the rate of active dissolution, the degree of passivity, the existence of transpassive dissolution and with obtaining information for further experiments to investigate the given system. Also, polarization curves can be used for semi-quantitative interpretation of active and active-passive transition ranges.
For non-steady state techniques, time dependent conditions are likely to provide a further insight into the elementary processes controlling the steady state. In principle, the non-steady state of the system can be calculated, and then compared to the experimental data, provided the equations governing the time dependence of any state determining variables are known. For electrochemical kinetic studies, linear sweep, rectangular step and periodic potential or current time functions are frequently used. Although these techniques generally give rise to very complicated analysis when applied to passivity, valuable information can be obtained with regard to the nature of the passive state.
Many experiments have revealed that at short times the disturbed electrode- electrolyte interface, even in the passive state, behaves much like a parallel R-C circuit in series with the electrolyte resistance Re. Therefore, step techniques are suited to Re and C measurements. A current step ΔI forced into the system at t = 0 gives rise to a potential
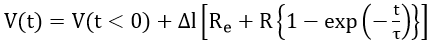
where 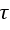
At very short times (t << RC) equation (18) reduces to
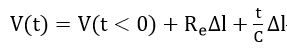
Equation (19) allows Re and C to be determined from the initial step and the initial slope of the I(t) curve.
In the same manner, a potentiostatic step ΔV leads to a current-time response given by
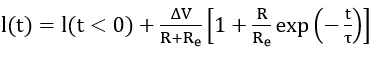
that at very short times reduces to
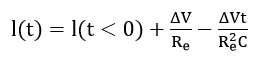
Re can be calculated from the initial peak current and the capacitance from either the area under the I(t) curves or from a semi-logarithmic I(t) plot.
At longer times, the interface behaves in a much more complicated fashion. Surface concentrations, partial coverages, and layer properties can no longer be regarded as being frozen into their initial state, and they start changing with time. If step techniques are used, the state determining variables tend toward new steady values and the current or the potential does likewise. Potential step techniques are particularly suited for developing the laws governing layer formation under constant potential conditions. Theoretical laws can be derived for various mechanisms of conduction and film growth when coupled with electrochemical theory.
The basic electrodic equation which has been found to describe the current- electrode potential behaviour of an activation controlled reaction is the Buttler-Volmer equation. Consider the simplest reaction, an elementary one-step electrodic reaction: the electrode donates an electron to the electron-acceptor ion A+. After the receipt of the electron, the electron acceptor is transformed into a new substance D
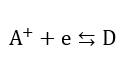
The Buttler-Volmer equation for this system can be derived in the form[14][55]
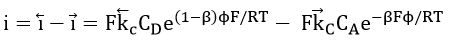
where 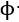
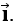

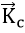
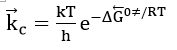
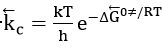
where 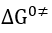
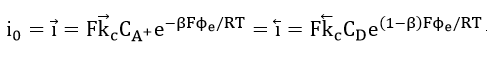
where 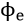
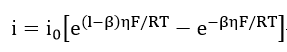
where 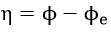
At low overpotential, this tends to zero and the expansion of each exponential terms in equation (26) results in the relation
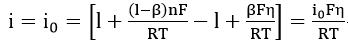
where only first order terms were retained.
At high fields, the Buttler-Volmer equation yields the anodic and the cathodic Tafel equations,

and
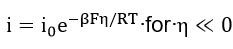
At equilibrium potential, it follows from equation (25) that
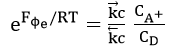
Upon taking logarithms
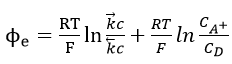
Equation (31) can be written in the form
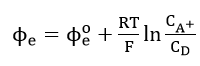
by defining
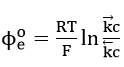
which is the standard value of when the concentration ratio is unity. Thus, the Buttler-Volmer equation reduces to the Nernst equation (32) at equilibrium potential.
The mixed potential theory derived by Wagner and Traud[56] is also one of the most important concepts in corrosion theory. The mixed potential theory consists of two simple hypotheses:
- any electrochemical reaction can be divided into two or more partial oxidation and reduction reactions.
- there can be no accumulation of electrical charge during an electrochemical reaction.
For the pair of electrochemical reactions
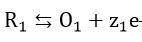
and
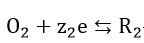
which occur concurrently, the relationship between current density i and potential can be written as
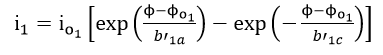
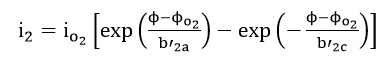
Each of the reactions, equations (34) and (35), has a characteristic reversible potential and an exchange current density . The corrosion potential is a mixed potential which must be between the reversible potentials of the individual reactions, equations (34) and (35)
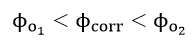
According to mixed potential theory, the current i at any potential is given as the sum of all the partial currents for the reactions in equations (34) and (35).
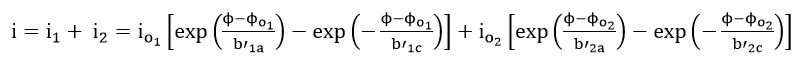
If the corrosion potential does not lie close to the reversible potential of either of the two reactions, equation (39) is reduced to
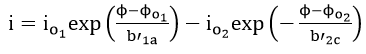
The corrosion current density can be defined as
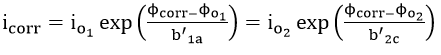
Combining equations (40) and (41) leads to
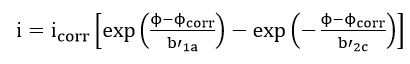
The derivation of equation (42) assumed:
a) The Buttler-Volmer equations of electrochemical kinetics are applicable.
b) Ohmic drops in the electrolyte and in surface films are absent.
c) Concentration polarization is absent.
d) Corrosion potential does not lie close to the reversible potential of either of the two reactions.
e) The whole metal functions simultaneously as a cathode and an anode.
f) There are no secondary electrochemical reactions occurring.
3.1. Corrosion rate measurement
The rate of corrosion taking place at the metal-medium interface can be determined by two different methods. One is by a weight change method and the other is by an electrochemical method. In electrochemical measurements, mixed potential theory forms the basis to determine the corrosion rate.
3.1.1. Weight loss method
Recording the weight loss of corroded metals is the most widely used method for evaluating the corrosion of metals quantitatively[57][58]. This is a simple straightforward method which shows the amount of metal removed over a given time period under specified conditions. This method cannot be applied if the corrosion is highly selective, such as intergranular corrosion or deep pitting. In the first case, it is difficult to remove the products of corrosion and in the second the depth of the pit may be the most important factor which affects the service life of the metal more than the loss in weight. The corrosion rate is expressed in various units, for instance:
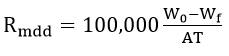
where 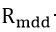
The accuracy of the weight loss method depends on how completely the corrosion products are removed from the specimens and how much the non-corroded metal is dissolved in the cleaning reagent. The method by which the products of corrosion are removed depends on the properties of the metal and the corrosion product. Some of
the most extensively used solutions and processes for the chemical removal of corrosion products are found in references[57][58][59].
The report for corrosion rate should, therefore, include the composition and the size of specimens, the surface preparation, and the post corrosion cleaning method.
3.1.2. Tafel extrapolation method
This method uses data obtained from cathodic or anodic polarization measurements. In general, cathodic polarization data are preferred since these are easier to measure experimentally. Theoretically, this method is based on the mixed potential theory. If logarithms are taken on both sides of equation (42) for large cathodic polarization potentials,
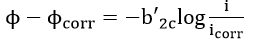
Thus, in order to determine corrosion rates from polarization measurements, the Tafel region is extrapolated to the corrosion potential. At the corrosion potential, the rate of cathodic reaction is equal to the rate of metal dissolution, and this point corresponds to the corrosion rate of the system expressed in terms of current density. In actual practice, a polarization curve becomes linear on a semi-logarithmic plot at approximately 50 mV more active than the corrosion potential.
Under ideal conditions, the accuracy of the Tafel extrapolation method is equal to or greater than conventional weight-loss methods. With this technique it is possible to measure extremely low corrosion rates, and it can be used to continuously monitor the corrosion rate of a system. Although it can be performed rapidly with high accuracy, there are restrictions which must be met before this method can be used. To ensure reasonable accuracy, the Tafel region must extend over a current range of at least one order of magnitude. Further, the method can only be applied to systems containing one reduction process, since usually the Tafel slope is distorted if more than one reduction process occurs. And as the test electrode has to be polarized over a wide range of potentials and currents in order to obtain Tafel lines, the possible reactions at large polarizations might change the test electrode surface and lead to the wrong experimental values.
3.1.3. Linear polarization method
The polarization resistance method[60][61][62][63] is a fast, sensitive, and non-destructive test for the evaluation of instantaneous corrosion rate.
Differentiation of equation (42) with respect to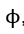
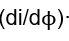
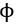
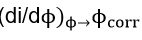

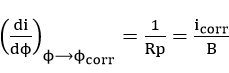
where
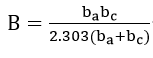
is a constant which contains Tafel slope information.
For the special case when the cathodic reaction is diffusion controlled, b2c approaches an infinite value and is given as
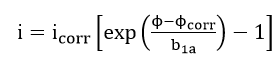
The corresponding slope for the polarization curve at the corrosion potential is
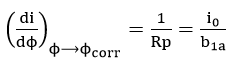
The polarization resistance method avoids most of the problems associated with extensive polarization since only the region close to the open circuit potential is of interest. But from equation (45) it is evident that for the calculation of corrosion rate,, the value of B needs to be determined. Tafel slope values could be estimated from high polarization data, but the method becomes redundant because corrosion rate can be estimated directly by Tafel extrapolation. To overcome this criticism, recent research has been concerned with determining Tafel slopes from low polarization data, such as the two and three point method of Barnartt [63] and the graphical fitting and computer analysis methods of Mansfeld[64]. The assumptions for the derivation of equation (45) become limitations for the use of the linear polarization method[65][66][67]. The potential at which linearity occurs was also found to be
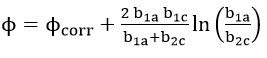
Therefore, the potential of linearity lies at the corrosion potential only for the case of equal anodic and cathodic Tafel slopes.
3.1.4. Three point method
Barnartt[63] has proposed a three point method to determine Tafel slopes and corrosion rates. This technique is general and applicable within any potential range, especially in the vicinity of the corrosion potential. The analysis operates on three selected polarization measurements, at potential changes 
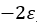
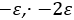

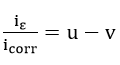
where u and v can be identified by comparing with equation (42),
Then, the relations
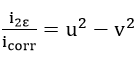
and
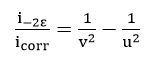
are easily derived.
If we denote the current ratio as
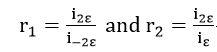
it is readily shown that these ratios are interrelated through the quadratic equation
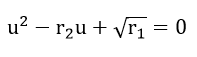
One root gives the numerical value of , the other of . With the Tafel slopes known, can be easily obtained. One advantage of this method is that since there are only short pulses applied to the test electrode, no changes of the surface result from the measuring process. Since this method is very sensitive to the values of current, the
calculated parameters become more accurate as the accuracy of the meter current increases.
3.2. Effect of polarization rate
During the rapid development and application of potentiostatic polarization methods, the effect of scan rate has received little attention. Since most polarization measurements are not conducted under steady state conditions, it is likely that experimental duration and other time factors influence results.
In general, at faster polarization rates, current densities tend to be higher and the passivating potential becomes more noble. The observed logarithmic variation of critical and passive current densities with polarization rate can be expressed by a relation of the form
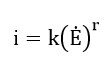
where k and r are constants. Polarization rate sensitivity r commonly has values between one-half and two.
Fontana et al. [68] studied the theoretical significance of equation (55) by means of the classical electrical circuit representation of a passive film. The passive current i is then given by
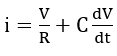
where R is a resistance, C is a capacitance, and V is the potential difference across the passive film. Under transient conditions, the capacity term of equation (56) predominates, and the resistive term may be neglected. Hence, at fast polarization rates, the influence of polarization rate on the passive current may be approximated by
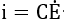
assuming that polarization rate reflects a change of the potential in the film. With slow polarization rates, the capacitive term may be neglected. The electrical behaviour of the passive film is assumed to obey Ohm’s law, and the resistance increases in proportion to the film thickness. The film thickness is proportional to the total charge passed, it, and hence the time function of its resistance can be written as
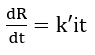
The dependence of the passive current on polarization rate at slow polarization rates may now be determined by substituting the time functions for potential and resistance into Ohm’s law:
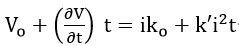
Since , equation (59) simplifies to
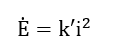
or
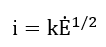
Intermediate values between one-half and one are expected at moderately fast polarization rates from a summation of fractional contributions from capacitive and resistive elements.
A more refined electrical model may be required to explain the upper limit value for polarization rate sensitivity, but this simple model provides guidance to select slow polarization rates for a given experimental condition.
If the polarization is made sufficiently slow to nearly correspond to a steady-state, the ambiguity in the polarization curve due to non-steady state conditions can be eliminated. However, there are problems associated with such measurements when applied to systems with active-passive transitions. The achievement of steady state conditions in active-passive systems usually requires very long time intervals. In many applications, the measurement of steady state polarization data is not only tedious, but undesirable. The determination of passivating current requirements for anodic protection applications necessitates rapid polarization measurements since passivation occurs under non- steady state conditions. This also applies to development of self-passivating alloys, since these systems must passivate rapidly to avoid excessive corrosion. At slower polarization rates, the specimen is, in certain instances, etched while passing through the region of active potential prior to reaching the passive potential[19][69].
The best or most accurate method for measuring potentiostatic anodic polarization behaviour depends on its intended use. However, measurements should be conducted as slowly as possible, even though only qualitative data are required. High polarization rates tend to obscure the passive region and other features of the polarization curves. Fontana et al.[68] observed that minimum passive current density, minimum secondary passive current density and maximum current density preceding secondary passivation converge at a polarization rate of less than 20 mV/min for iron in 1N H2SO4 solution. They proposed that this polarization rate can be regarded as the fastest steady-state polarization rate for the system.
3.3. Effect of cathodic pretreatment
Cathodic pretreatment for surface preparation of the specimen is a common procedure in electrochemical experiments. Cathodic pretreatment increases the magnitude of the critical anodic current density without noticeably influencing passivating potential and passive current densities. The effect of cathodic pretreatment becomes more pronounced with longer pretreatment times, and with more active pretreatment potentials[70][71].
Kim and Wilde[71] studied the cathodic reaction at the active pretreatment potential for stainless steel in dilute H2SO4. One of their concerns was the liberation of mono-atomic hydrogen which may either combine to form molecular hydrogen or be absorbed into the bulk metal. On subsequent anodic polarization after cathodic pretreatment, when the electrode potential became more noble than the reversible hydrogen potential, the observed current density would be the sum of the rates of two processes: metal dissolution and hydrogen oxidation. The rate of hydrogen oxidation will be governed by two interdependent processes: the kinetics of the oxidation of hydrogen on the passive surface and the rate of diffusion of hydrogen to the surface from the bulk. For the oxidation reaction of hydrogen, the net anodic current, i, becomes:
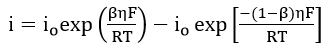
Assuming , equation (62) reduces to
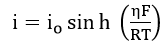
Therefore, i should increase rapidly with increasing , but because of concentration, polarization will reach a limiting value.
For hydrogen diffusion, Kim and Wilde [71] obtained the equation for the quantity of hydrogen, Q, remaining in the specimen on the assumption that the surface concentration of hydrogen is zero at all times during the anodic polarization of cylindrical specimens.

where D is the diffusivity of hydrogen, l and r are the length and diameter of the electrode, respectively, and is the root of the zero order Bessel function of the first kind. Thus, the rate of extraction becomes
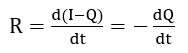
which can be evaluated from the slope of a plot of Q vs. t. At low overpotentials, the diffusion rate of hydrogen to the surface will be high compared to the rate of oxidation. Then the net hydrogen partial current will be given by
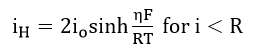
At overpotentials where the hydrogen diffusion rate to the surface becomes less than the possible oxidation rate, the hydrogen partial current will be controlled by diffusion to the surface
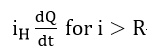
The general shape of the curve based on the above considerations is the same as the polarization curve of active-passive transition metals[71].
For low pH solutions, this effect sometimes gives two resolved peaks in the active-passive transition range of the polarization curve. Therefore, cathodic pretreatment should be used only if it reflects the actual system under study. Hydrogen released by pretreatment should be removed before determining the polarization curves, especially for acidic solutions.
4. Non-electrochemical Methods
Application of non-electrochemical techniques such as AES, ESCA, ellipsometry, etc. provides information on thickness, structure, composition and properties of the passive film. Special advantages or disadvantages of specific techniques are well summarized by Leidheiser and references therein[72].
AES and ESCA are two non-electrochemical techniques which were employed by our Group in a study on the passivity of AISI 316 stainless steel[73]. Generally, ESCA and AES are considered as separate types of spectroscopy, but the information contained in both methods is very similar. ESCA electrons are emitted as a result of primary photoionization events while Auger electrons come from secondary electron emission.
The main advantages of AES and ESCA are as follows:
- Essentially non-destructive techniques.
- High sensitivity and modest sample requirements.
- Capability of studying solids, liquids and gases.
- Materials may be studied in situ in their working environments with a minimum of preparation.
- large amount of information is available from a single experiment.
- For solids, there is a unique capability of differentiating surface from subsurface and bulk phenomena. Analytical depth profiling possible.
- Information levels are such that investigations are feasible ab initio.
- Data are often complementary to that obtained by other techniques.
- Theoretical basis is well understood and results may be quantified.
The time scales involved are so short that the interpretation of data is within sudden approximation and thus involves time-independent quantum mechanical treatments. The extremely rapid time scale of ESCA and AES as a spectroscopic technique is also one of its advantages.
Figure 1 is an electron energy level diagram of a solid illustrating the mechanisms necessary for emission of photoelectrons or Auger electrons. In the upper part of the diagram, a photon is absorbed such that
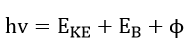
where hv is the photon energy, is the electron kinetic energy, is the electron binding energy and is the work function of the spectrometer. The binding energy is defined as the energy difference between the Fermi level and the ground state of the electron that has been removed. As the photon energy is known and the analyzer work function is predetermined, a plot can be made of the number of electrons vs. electron binding energies. Photoelectron binding energies are unique and can be used to identify specific elements.
The Auger process is demonstrated in the lower portion of Figure 1. In this case, a core level electron can be removed with either photons or electrons. When a core level electron (K shell) is removed, an outer shell electron (L shell) will fill the core level vacancy. As the atom is in an excited state at this stage with a gain in energy, it becomes stabilized to ground state with emission of an Auger electron or a photon. The kinetic energy of the KLL Auger electron in Figure 1 is
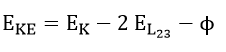
where is the energy level of K orbital. An Auger electron peak represents the energy characteristic of a specific atom. While it is true that the core ionization energies of a particular atom are sufficiently invariant to provide a fingerprint of the atom, there are nonetheless small but measurable changes with the chemical environment of the atom. In other words, core electron ionization energies show a chemical shift effect when data from a range of compounds containing the atom in question are compared. Chemical shift is important to distinguish three situations: molecular compounds containing non-equivalent atoms of the same element, solid materials having atoms of a given element with non-equivalent lattice sites and the comparison of ionization energy data for different compounds.
In the quantification of AES and ESCA, parameters such as excitation cross section, electron escape depth dependence on energy, analyzer transmission function and chemical and physical inhomogeneities must be accounted for.
In general, the photoelectron peak intensity produced by sub-shell k can be calculated by integrating the differential intensities originating in the various volume elements of the specimen.
Each of these differential intensities can be written as the following product, in which x, y, z denotes position within the specimen[74]:
Figure 1. Energy level diagrams of photoelectron (top) and Auger electron (bottom) excitation.
With a few simplifying assumptions the total peak intensity is readily obtained. For integration, the specimen is assumed to be atomically flat, and polycrystalline to avoid single crystal anysotropies. An exponential inelastic attenuation law is assumed, and a mean solid angle is also assumed applicable over all specimen volumes. Within the approximations quoted above, which are very nearly achieved in a number of practical spectrometer systems, it is possible to derive intensity expressions for several important cases[74]: semi-infinite specimens with atomically clean surfaces, specimens of limited thickness with atomically clean surfaces, semi-infinite substrates with uniform overlayers of limited thickness, and semi-infinite substrates with a non-attenuating overlayer at fractional monolayer coverages. The integrated peak photoelectron current, Ip, to the number of atoms per unit volume, n, 
where k is a constant, is the photoelectron cross-section and is the electron escape depth. Sometimes the energy separation of the lines in ESCA and AES spectra is not large enough to allow these quantities to be determined without a graphical resolution of the obtained structure. If the line shapes and binding energies of unresolved lines are known, deconvolution or curve fitting can be carried out. Typical functions for line shape are Gaussian, Lorentzian and intermediate forms. A good approximation of an ESCA line was found as the intermediate form[75], but a pure Gaussian or a pure Lorentzian could also be used without large error.
5. Conclusions
Passivity is the state of a metal or an alloy in aqueous solution (or in some organic solvents) where the surface is covered by a thin, compact, and adherent oxide or oxihydride film which protects the metal or alloy against corrosion. Passivity is of direct relevance to materials science and engineering, as the presence of a passive film on the surface of the metallic material gives it a natural protection against corrosion.
The phenomenon of passivation was already known in the 19th century. Since that time, the various aspects of the passivation of metals and alloys have been extensively investigated using the new methods that gradually became available. The literature on passivation, including papers in scientific journals, conference proceedings, and books, is extremely abundant, even in modern times[76][77][78][79][80][81][82][83][84][85][86][87][88][89].
The objective of this article was not to review the published work on passivation in an exhaustive manner but rather to provide the reader with the basic concepts and theories necessary to understand what passivity is, and to describe the classical experiments used to determine the mechanism underlying the produced passivation and its cause, as well as to understand the surface changes resulting in the active-passive transition.
This entry is from: http://www.scielo.mec.pt/pdf/cpm/v29n4/v29n4a03.pdf
References
- C. Wagner, Corros. Sci., 5, 751 (1965).
- H. H. Uhlig and P. F. King, J. Electrochem. Soc., 106, 1 (1959).
- E. McCafferty, Corros. Sci., 50, 3622 (2008).
- D. D. MacDonald, ECS Transactions,
- E. McCafferty, J. Electrochem. Soc., 154, C571 (2007).
- E. McCafferty, Corros. Sci., 44, 1393 (2002).
- E. McCafferty, J. Electrochem. Soc., 149, B333 (2002).
- E. McCafferty, Corros. Sci., 42, 1993 (2000).
- E. McCafferty, Electrochem. Solid St., 3, 28 (2000).
- V. S. Beleevskij and Yu. I. Kudelin, Zashchita Metallov, 28, 231 (1992).
- Yu. A. Popov and Yu. A. Alekseev, Soviet Electrochem., 21, 457 (1985).
- P. Zaya and M. B. Ives, Thin Films Sci.Technol., 287 (1983).
- R. B. Diegle and J. E. Slater, Corrosion, 32, 155 (1976).
- K. J. Vetter, (Electrochemical Kinetics – Theoretical and Experimental Aspects), Academic Press, New York, USA (1967).
- U. R. Evans, J. Chem. Soc. (London), 1020 (1927).
- M. Fleischmann and H. R. Thirsk, J. Electrochem. Soc., 110, 688 (1963).
- L. Tronstad and C. Borgmann, Trans. Faraday Soc., 30, 349 (1934).
- T. S. de Gromoboy and L. L. Shreir, Electrochim. Acta, 11, 895 (1966).
- R. P. Frankenthal, J. Electrochem. Soc., 116, 580 (1969); 116, 1646 (1969).
- H. H. Uhlig (Passivity of Metals), R. P. Frakenthal and J. Kruger, eds., The Electrochem. Soc., p. 1 (1978).
- H. H. Uhlig (Corrosion and Corrosion Control), John Wiley & Sons, Inc., N. Y., USA (1971).
- N. Sato (Passivity of Metals), R. P. Frankenthal and J. Kruger, eds., The Electrochem. Soc., p. 29 (1978).
- R. D. Armstrong, Corros. Sci., 11, 693 (1971).
- N. F. Mott, Trans. Faraday Soc., 35, 1175 (1939).
- N. Cabrera and N. F. Mott, Rep. Prog. Phys., 12, 1948 (1948-1949).
- R. Ghez, J. Chem. Phys., 58, 1838 (1973).
- N. Sato and M. Cohen, J. Electrochem. Soc. 111, 512 (1964).
- A. H. Lanyon and B. M. W. Trapnell, Proc. Roy. Soc., 227A, 387 (1955).
- N. Sato and T. Notoya, J. Electrochem. Soc., 114, 585 (1967).
- P. Fehlner and N. F. Mott, Oxid. of Metals, 2, 59 (1970).
- H. H. Uhlig, Acta Met., 4, 541 (1956).
- O. H. Hamilton and H. A. Miley, Trans. Electrochem. Soc., 81, 416 (1942).
- T. B. Grimley and B. M. W. Trapnell, Proc. Roy. Soc., A234, 405 (1956).
- O. Kubaschewski and B. E. Hopkins, (Oxidation of Metals and Alloys) Butterworth Scientific Publications, N.Y., USA (1953).
- P. T. Landsberg, J. Chem. Phys., 23, 1079 (1955).
- D. D. Eley and P. R. Wilkinson, Proc. Roy. Soc., A254, 327 (1960).
- C. Wagner, Z. Phys. Chem., B21, 25 (1933).
- P. Kofstad (High Temperature Oxidation of Metals), John Wiley and Sons, Inc., N. Y., USA (1966).
- A. T. Fromhold Jr., J. Phys. Chem. Solids, 24, 1309 (1963).
- Y. M. Kolotyrkin and N. Y. Bune, Z. Phys. Chem., 214, 1309 (1963).
- S. K. R. S. Sankaranarayanan and S. Ramanathan, Phys. Rev. B – Cond. Matter. Mat. Physics, 78, 085420 (2008).
- M. Okuyama, S. Kambe and D. L. Piron, Mater. Sci. Forum 192-194, 489 (1995).
- J. Haefele, B. Heine and R. Kirchheim, Z. Metall./Mat. Res. Adv. Tech., 83, 395 (1992).
- V. Koenig and J. W. Schultze, Werk. Korros., 39, 595 (1988).
- M. Lakatos-Varsányi and W. Meisel, J. Radioanal. Nucl. Chem., 251, 75 (2002).
- O. N. Nechaeva, V. P. Grigoriev and A. A. Popova, Z. Metall., 4, 553 (1992).
- A. Baraka, R. M. S. Baraka and A. Abdel-Razik, Surf. Technal., 26, 199 (1985).
- C. Y. Chao and Z. Szklarska- Smialowska, Surf. Sci., 96, 426 (1980).
- A. Baraka, A. I. Abdel-Rohman and A. A. El Hosary, Brit. Corros. J., 11, 44 (1976).
- C. Cuevas-Arteaga and J. Porcayo- Caldéron, Mater. Sci. Eng. A, 435-436, 439 (2006).
- Y. Chen and D. D. MacDonald, Proc. Electrochem. Soc., PV2004-19, 289 (2006).
- C. Giacomelli, F. C. Giacomelli, R. L. Bortolluzi and A. Spinelli, Anti-Corros. Meth. Mater., 53, 232 (2006).
- S. Fujimoto and T. Shibata, Mater. Sci. Forum, 185-188, 741 (1995).
- C. M. Abreu, M. J. Cristóbal, R. Losada, X. R. Nóvoa, G. Pena and M. C. Pérez, J. Electroanal. Chem., 572, 335 (2004).
- A.J. Bard and L.R. Faulkner, (Electrochemical Methods: Fundamentals and Applications) 2nd ed., John Wiley and Sons, New York, USA, (2001).
- C. Wagner and W. Traud, Z. Elektrochem., 44, 391 (1938).
- V. V. Romanov (Corrosion of Metals), Israeli Program for Scientific Translations, Jerusalem, Israel (1969).
- American Society for Testing and Materials, Yearbook, G1-67, 928 (1973).
- H. H. Uhlig (The Corrosion Handbook), John Wiley and Sons, Inc., N. Y., USA (1948).
- M. Stern and A. L. Geary, J. Electrochem. Soc., 104, 56 (1957).
- F. Mansfeld (Advances in Corrosion Science and Technology) M.G. Fontana and R.W. Staehle, eds., Plenum Press, N. Y., USA, 6, (1976).
- G. W. Walter, Corros. Sci., 17, 983 (1977).
- S. Barnartt (Electrochemical Techniques for Corrosion), R. Baboian, ed., London, UK, (1977).
- F. Mansfeld, J. Electrochem. Soc., 120, 515 (1973).
- A. C. Markrides, Corrosion, 29, 148 (1973).
- R. H. Hansler, Corrosion, 33, 177 (1977).
- M. E. Indig and C. Groot, Corrosion, 25, 455 (1969).
- J. E. Reinoehl, F. H. Beck and M. G. Fontana, Corrosion, 26, 141 (1970).
- R. Littlewood, Corros. Sci., 3, 99 (1963).
- N. D. Green and R. B. Leonard, Electrochim. Acta, 9, 45 (1964).
- C. D. Kim and B. E. Wilde, Corros. Sci., 10, 735 (1970).
- H. Leidheiser Jr. (Passivity of Metals), R. P. Frankenthal and J. Kruger, eds., The Electrochem. Soc., p. 223 (1978).
- C. A. C. Sequeira, D. M. F. Santos, J. R. Sousa and P. S. D. Brito, ECS Transactions, 16(48), 67 (2009).
- R.C. Salvarezza, N. de Cristofaro, C. Pallota and A.J. Arvia, Electrochim. Acta, 32, 1049 (1987).
- K. Siegbahn, C. Nordling, G. Johansson, J. Hedman, P. F. Heden, K. Hamrin, U. Gelius, T. Bergmark, L. O. Werme, R. Manne and Y. Maer, ESCA Applied to Free Molecules, Elsevier Pub., N.Y., USA (1969).
- C. A. C. Sequeira (Uhlig’s Corrosion Handbook), R. W. Revie, ed., John Wiley and Sons, New York, USA, p. 729 (2000).
- G. Wedler, Lehrbuch der Physikalischen Chemie, Wiley-VCH, Weinheim (1997).
- P. Druska, H.-H. Strehblow and S. Golledge, Corros. Sci., 38, 1369 (1996).
- K. E. Heusler, ed., Passivation of Metals and Semiconductors, Mater. Sci. Forum, 185-188 (1995).
- P. M. Natishan, R. G. Kelly, G. S. Frankel and R. C. Newman, eds., Critical Factors in Localized Corrosion, Electrochemical Society Proc. Series, PV95-15, Pennington, NJ (1995).
- F. Di Quarto, S. Piazza and C. Sunseri in Modifications of Passive Films (P. Marcus, B. Baroux and K. Keddam, eds.), The Institute of Materials, London, EFC Vol. 12, p. 76 (1994).
- M. Bojinov, G. Fabricius, T. Laitinen, T. Saario and G. Sundholm, Electrochim. Acta, 44, 247 (1998).
- V. Maurice, H. H. Strehblow and P. Marcus, J. Electrochem. Soc., 146, 524 (1999).
- P. Schmuki, S. Virtanen, A. J. Davenport and C. M. Vitus, J. Electrochem. Soc., 143, 3997 (1996).
- P. Marcus and F. Mansfeld, eds., (Analytical Methods in Corrosion Science and Engineering), CRC Press, Boca Raton, FL , USA (2006).
- L. L. Shreir, R. A. Yarman and G.T. Burstein, eds., (Corrosion, Metal/En- vironment Reactions), 3rd ed., Butterwor- th-Heinemann, New York, USA (1994).
- C. A. C. Sequeira, Brit. Corros. J., 30(2), 137 (1995).
- C. A. C. Sequeira (Enciclopédia Luso-Brasileira de Cultura), Edição Século XXI, Editorial Verbo, Lisboa, Vol. 22, p. 308 (2002).
- C. A. C. Sequeira and D. M. F. Santos, J. Appl. Electrochem., 40, 123 (2010).