
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Sirius Huang | -- | 1326 | 2022-11-25 01:42:54 | | | |
| 2 | Sirius Huang | Meta information modification | 1326 | 2022-11-28 10:14:59 | | |
Video Upload Options
In set theory, the complement of a set A, often denoted by Ac (or A′), is the set of elements not in A. When all sets in the universe, i.e. all sets under consideration, are considered to be members of a given set U, the absolute complement of A is the set of elements in U that are not in A. The relative complement of A with respect to a set B, also termed the set difference of B and A, written [math]\displaystyle{ B \setminus A, }[/math] is the set of elements in B that are not in A.
1. Absolute Complement

1.1. Definition
If A is a set, then the absolute complement of A (or simply the complement of A) is the set of elements not in A (within a larger set that is implicitly defined). In other words, let U be a set that contains all the elements under study; if there is no need to mention U, either because it has been previously specified, or it is obvious and unique, then the absolute complement of A is the relative complement of A in U:[1] [math]\displaystyle{ A^c = U \setminus A. }[/math]
Or formally: [math]\displaystyle{ A^c = \{ x \in U : x \notin A \}. }[/math]
The absolute complement of A is usually denoted by Ac. Other notations include [math]\displaystyle{ \overline A, A', }[/math][2] [math]\displaystyle{ \complement_U A, \text{ and } \complement A. }[/math][3]
1.2. Examples
- Assume that the universe is the set of integers. If A is the set of odd numbers, then the complement of A is the set of even numbers. If B is the set of multiples of 3, then the complement of B is the set of numbers congruent to 1 or 2 modulo 3 (or, in simpler terms, the integers that are not multiples of 3).
- Assume that the universe is the standard 52-card deck. If the set A is the suit of spades, then the complement of A is the union of the suits of clubs, diamonds, and hearts. If the set B is the union of the suits of clubs and diamonds, then the complement of B is the union of the suits of hearts and spades.
1.3. Properties
Let A and B be two sets in a universe U. The following identities capture important properties of absolute complements:
De Morgan's laws:[4]
- [math]\displaystyle{ \left(A \cup B \right)^c=A^c \cap B^c. }[/math]
- [math]\displaystyle{ \left(A \cap B \right)^c=A^c\cup B^c. }[/math]
Complement laws:[4]
- [math]\displaystyle{ A \cup A^c = U . }[/math]
- [math]\displaystyle{ A \cap A^c =\varnothing . }[/math]
- [math]\displaystyle{ \varnothing^c =U. }[/math]
- [math]\displaystyle{ U^c =\varnothing. }[/math]
- [math]\displaystyle{ \text{If }A\subseteq B\text{, then }B^c\subseteq A^c. }[/math]
- (this follows from the equivalence of a conditional with its contrapositive).
Involution or double complement law:
- [math]\displaystyle{ \left(A^c\right)^c = A. }[/math]
Relationships between relative and absolute complements:
- [math]\displaystyle{ A \setminus B = A \cap B^c. }[/math]
- [math]\displaystyle{ (A \setminus B)^c = A^c \cup B = A^c \cup (B \cap A). }[/math]
Relationship with a set difference:
- [math]\displaystyle{ A^c \setminus B^c = B \setminus A. }[/math]
The first two complement laws above show that if A is a non-empty, proper subset of U, then {A, Ac} is a partition of U.
2. Relative Complement
2.1. Definition
If A and B are sets, then the relative complement of A in B,[4] also termed the set difference of B and A,[5] is the set of elements in B but not in A.
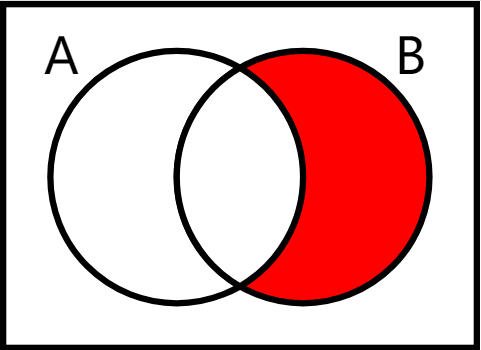
The relative complement of A in B is denoted [math]\displaystyle{ B \setminus A }[/math] according to the ISO 31-11 standard. It is sometimes written [math]\displaystyle{ B - A, }[/math] but this notation is ambiguous, as in some contexts (for example, Minkowski set operations in functional analysis) it can be interpreted as the set of all elements [math]\displaystyle{ b - a, }[/math] where b is taken from B and a from A.
Formally: [math]\displaystyle{ B \setminus A = \{ x\in B : x \notin A \}. }[/math]
2.2. Examples
- [math]\displaystyle{ \{ 1, 2, 3\} \setminus \{ 2,3,4\} = \{ 1 \}. }[/math]
- [math]\displaystyle{ \{ 2, 3, 4 \} \setminus \{ 1,2,3 \} = \{ 4 \} . }[/math]
- If [math]\displaystyle{ \mathbb{R} }[/math] is the set of real numbers and [math]\displaystyle{ \mathbb{Q} }[/math] is the set of rational numbers, then [math]\displaystyle{ \mathbb{R}\setminus\mathbb{Q} }[/math] is the set of irrational numbers.
2.3. Properties
Let A, B, and C be three sets. The following identities capture notable properties of relative complements:
-
- [math]\displaystyle{ C \setminus (A \cap B) = (C \setminus A) \cup (C \setminus B). }[/math]
- [math]\displaystyle{ C \setminus (A \cup B) = (C \setminus A) \cap (C \setminus B). }[/math]
- [math]\displaystyle{ C \setminus (B \setminus A) = (C \cap A) \cup (C \setminus B), }[/math]
- with the important special case [math]\displaystyle{ C \setminus (C \setminus A) = (C \cap A) }[/math] demonstrating that intersection can be expressed using only the relative complement operation.
- [math]\displaystyle{ (B \setminus A) \cap C = (B \cap C) \setminus A = B \cap (C \setminus A). }[/math]
- [math]\displaystyle{ (B \setminus A) \cup C = (B \cup C) \setminus (A \setminus C). }[/math]
- [math]\displaystyle{ A \setminus A = \empty. }[/math]
- [math]\displaystyle{ \empty \setminus A = \empty. }[/math]
- [math]\displaystyle{ A \setminus \empty = A. }[/math]
- [math]\displaystyle{ A \setminus U = \empty. }[/math]
- If [math]\displaystyle{ A\subset B }[/math], then [math]\displaystyle{ C\setminus A\supset C\setminus B }[/math].
- [math]\displaystyle{ A \supseteq B \setminus C }[/math] is equivalent to [math]\displaystyle{ C \supseteq B \setminus A }[/math].
3. Complementary Relation
A binary relation [math]\displaystyle{ R }[/math] is defined as a subset of a product of sets [math]\displaystyle{ X \times Y. }[/math] The complementary relation [math]\displaystyle{ \bar{R} }[/math] is the set complement of [math]\displaystyle{ R }[/math] in [math]\displaystyle{ X \times Y. }[/math] The complement of relation [math]\displaystyle{ R }[/math] can be written [math]\displaystyle{ \bar{R} \ = \ (X \times Y) \setminus R. }[/math] Here, [math]\displaystyle{ R }[/math] is often viewed as a logical matrix with rows representing the elements of [math]\displaystyle{ X, }[/math] and columns elements of [math]\displaystyle{ Y. }[/math] The truth of [math]\displaystyle{ aRb }[/math] corresponds to 1 in row [math]\displaystyle{ a, }[/math] column [math]\displaystyle{ b. }[/math] Producing the complementary relation to [math]\displaystyle{ R }[/math] then corresponds to switching all 1s to 0s, and 0s to 1s for the logical matrix of the complement.
Together with composition of relations and converse relations, complementary relations and the algebra of sets are the elementary operations of the calculus of relations.
4. LaTeX Notation
In the LaTeX typesetting language, the command \setminus[6] is usually used for rendering a set difference symbol, which is similar to a backslash symbol. When rendered, the \setminus command looks identical to \backslash, except that it has a little more space in front and behind the slash, akin to the LaTeX sequence \mathbin{\backslash}. A variant \smallsetminus is available in the amssymb package.
5. In Programming Languages
Some programming languages have sets among their builtin data structures. Such a data structure behaves as a finite set, that is, it consists of a finite number of data that are not specifically ordered, and may thus be considered as the elements of a set. In some cases, the elements are not necessary distinct, and the data structure codes multisets rather than sets. These programming languages have operators or functions for computing the complement and the set differences.
These operators may generally be applied also to data structures that are not really mathematical sets, such as ordered lists or arrays. It follows that some programming languages may have a function called set_difference, even if they do not have any data structure for sets.
References
- The set in which the complement is considered is thus implicitly mentioned in an absolute complement, and explicitly mentioned in a relative complement.
- "Complement (set) Definition (Illustrated Mathematics Dictionary)". https://www.mathsisfun.com/definitions/complement-set-.html.
- Bourbaki 1970, p. E II.6.
- Halmos 1960, p. 17.
- Devlin 1979, p. 6.
- The Comprehensive LaTeX Symbol List. http://ctan.unsw.edu.au/info/symbols/comprehensive/symbols-a4.pdf





