1. Mean Characteristics

The mean characteristics of the three layers of the CBL are as follows.

Vertical profiles of mean variables in convective boundary layer. Adapted from Stull 1988 "An Introduction to Boundary layer meteorology" page 13. File:Vertical profile of mean variables in convective boundary layer.pdf - HandWiki

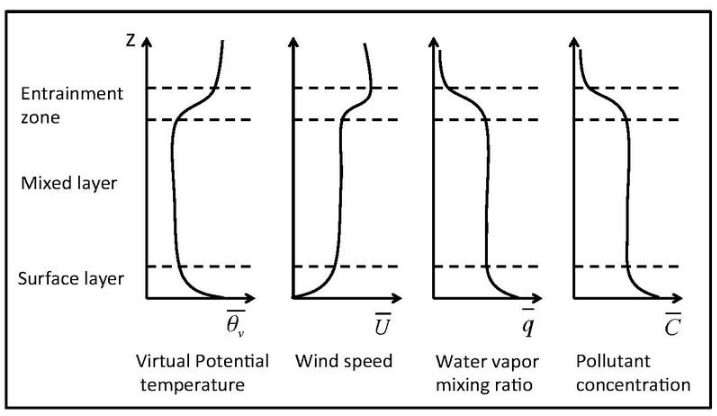
(1) The Surface layer is a very shallow region close to the ground (bottom 5 to 10% of CBL). It is characterized by a superadiabatic lapse rate, moisture decrease with height and strong wind shear.^[1] Almost all wind shear and all the potential temperature gradient in the CBL are confined in the surface layer.

(2) The Mixed layer composing the middle 35 to 80% of CBL^[1] is characterized by conserved variables such as potential temperature, wind speed and moisture.

(3) The Entrainment zone (or Capping inversion) can be quite thick, averaging about 40% of the depth of the CBL. It is the region of statically stable air at the top of the mixed layer, where there is entrainment of free atmosphere air downward and overshooting thermals upward.^[1] Potential temperature and wind speed have a sharp increase across the capping inversion, while moisture has a sharp decrease.

2. Evolution

CBL depth has a strong diurnal cycle with a 4-phase process growth^[2]

Evolution of convective boundary layer. Adapted from Stull 1988 "An Introduction to Boundary layer meteorology" page 11. File:Evolution of convective boundary layer.pdf - HandWiki

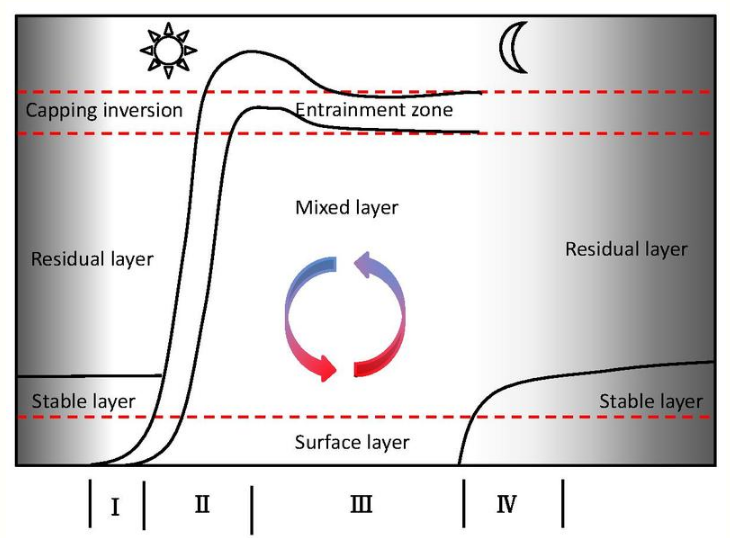
(1) Formation of a shallow mixed layer : During the early morning the mixed layer is shallow and its depth increases slowly because of the strong nocturnal stable inversion capping.^[3]

(2) Rapid growth : By the late morning, the cool nocturnal air has been warmed to a temperature near that of the residual layer, so the thermals penetrate rapidly upward during the second phase, allowing the top of the mixed layer to rise at rates of up to 1 km per 15 minutes.^[3]

(3) Deep mixed layer of nearly constant thickness : When the thermals reach the capping inversion at the top of the residual layer, they meet resistance to vertical motion and the mixed layer growth rate rapidly decreases. During this third phase, which spans over most of the afternoon, the mixed layer depth is relatively constant. The lapse rate of temperature in the CBL is 1°/100m.^[3]

(4) Decay : Turbulence generated by buoyancy which drives the mixing decays after sunset and CBL collapses as well.

3. Turbulence in the CBL

In the atmospheric boundary layer, wind shear is responsible for the horizontal transport of heat, momentum, moisture and pollutants, while buoyancy dominates for the vertical mixing. Turbulences are generated by buoyancy and wind shear. If the buoyancy dominates over shear production, the boundary layer flow is in free convection. When shear generated turbulence is stronger than those generated by buoyancy, the flow is in forced convection.

Normalized turbulent kinetic energy generated by buoyancy and shear by surface buoyancy. Adapted from Stull 1988 "An Introduction to Boundary layer meteorology" page 155. File:Buoyancy shear.pdf - HandWiki

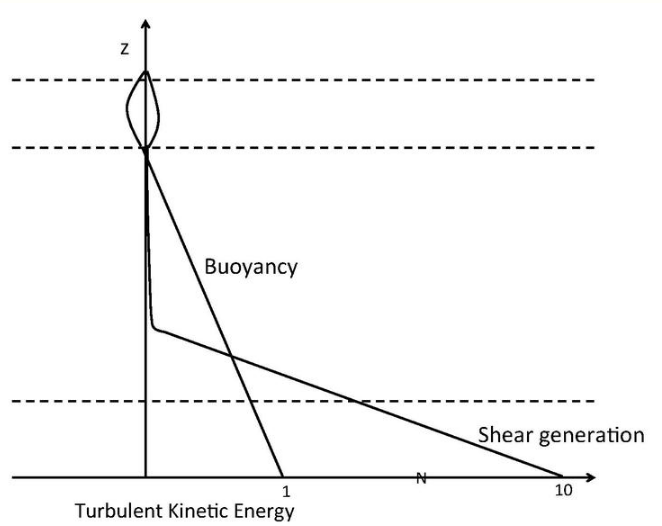
In the surface layer, shear production always exceeds buoyancy production because of strong shear generated by surface drag. In the mixed layer, buoyancy generated by heating from the ground surface is the major driver of convective turbulence.^[4] Radiative cooling from the cloud tops is also an effective driver of convection. The buoyancy generated turbulence peaks in the afternoon, hence the boundary layer flow is in free convection during most of the afternoon.

The up and downdrafts of boundary layer convection is the primary way in which the atmosphere moves heat, momentum, moisture, and pollutants between the Earth's surface and the atmosphere. Thus, boundary layer convection is important in the global climate modeling, numerical weather prediction, air-quality modeling and the dynamics of numerous mesoscale phenomena.

4. Model Simulation

4.1. Conservation Equation

To quantitatively describe the variation of quantities in the CBL, we need to solve the conservation equations. The simplified form of the conservation equation for a passive scalar in typical CBL is

[math]\displaystyle{ \frac {\partial \bar {c}}{\partial t}=-\frac {\partial \overline {w'c'}}{\partial z} }[/math]

where [math]\displaystyle{ \bar {c} }[/math] is the mean of quantity [math]\displaystyle{ c }[/math], which could be water vapor mixing ratio [math]\displaystyle{ q }[/math], potential temperature [math]\displaystyle{ \theta }[/math], eastward-moving [math]\displaystyle{ u }[/math] and northward-moving [math]\displaystyle{ v }[/math] wind speed. [math]\displaystyle{ \overline {w'c'} }[/math] is the vertical turbulent flux of [math]\displaystyle{ c }[/math].

We made several approximations to get the above simplified equation: ignore the body source, Bousinesq approximation, horizontal homogeneity and no subsidence. Bousinesq approximation is to ignore the density change due to pressure perturbation and keep the density change due to temperature change. This is a fairly good approximation in the CBL. The latter two approximations are not always effective in the real CBL. But this is acceptable in theoretical research. Observations show that turbulent mixing accounts for 50% of the total variation of potential temperature in a typical CBL.

However, due to the randomness of turbulences and our lack of knowledge about the exact physical behavior of it, parameterization of turbulent transport is needed in model simulation. Unlike shear dominated turbulence in the surface layer, large eddies associated with rise of warm air parcels that transport heat from hot to cold, regardless of the local gradient of the background environment exit in the mixed layer. Hence the non-local counter-gradient transport should be properly represented in the model simulation.

Several approaches are generally followed in numerical models to obtain the vertical profiles and temporal variations of quantities in CBL. Full mixing scheme for the whole CBL, local scheme for the shear dominated regions, non-local scheme and top-down and bottom up diffusion scheme for the buoyancy dominated mixed layer. In the full mixing scheme, all quantities are assumed to be uniformly distributed and the turbulent fluxes are assumed to be linearly related to height, with a jump at the top. In the local scheme, the turbulent flux is scaled by the local gradient of the quantity. In non-local scheme, the turbulence fluxes are related to known quantities at any number of grid points elsewhere in the vertical.^[5] In top-down and bottom-up diffusion, the vertical profile is determined by diffusion from the two directions and the turbulent fluxes in sub-grid scale are derived from known quantities or their vertical derivatives at the same grid point.

4.2. Full Mixing Scheme

Full mixing is the simplest representation of CBL in some global models. Fluxes within this layer are assumed to decrease linearly with height, and the mean variables keep their vertical profile at each simulation time step.^[6] All mean variables are uniformly distributed throughout the whole CBL and have a jump at the top of CBL. This simple model has been used in meteorology for a long time, and continues to be a popular approach in some global course resolution models.

4.3. Local Closure

The local closure K-theory is a simple and effective scheme for shear dominated turbulent transport in the surface layer. K-theory assumes that mixing for heat, water vapor and pollutant concentration occurs only between adjacent layers of the CBL, and that the magnitude of mixing is determined by the eddy diffusion coefficient [math]\displaystyle{ K_c }[/math] and local gradients of corresponding scalars [math]\displaystyle{ \frac{\partial c}{\partial z} }[/math].^[7]

[math]\displaystyle{ \overline{w'c'} = - K_c \frac{\partial c}{\partial z} }[/math]

Where [math]\displaystyle{ K_c }[/math] is an "eddy diffusion coefficient" for [math]\displaystyle{ c }[/math], which is typically taken as a function of a length scale [math]\displaystyle{ l_c }[/math] and local vertical gradients of [math]\displaystyle{ c }[/math]. For neutral condition, [math]\displaystyle{ K_c }[/math] is parameterized using Mixing-Length Theory.

[math]\displaystyle{ K_c = l_c^2 \left | \frac{\partial \bar{u}}{\partial z} \right \vert }[/math]

If a turbulent eddy moves a parcel of air upward by amount [math]\displaystyle{ z }[/math] during which there is no mixing nor other changes in the value of [math]\displaystyle{ c }[/math] within the parcel, then we define [math]\displaystyle{ l_c }[/math] by

[math]\displaystyle{ l_c = \kappa z }[/math]

where [math]\displaystyle{ \kappa }[/math] is the von Karman constant empirically derived (0.35 or 0.4).

Mixing-length theory has its own limitation. The theory only applies to statically neutral condition.^[8] It biases for statically stable and unstable conditions.

Mixing-length theory fails when the wind speed is uniformly distributed, people use knowledge of turbulent kinetic energy (TKE) to improve parameterization of eddy diffusion coefficient [math]\displaystyle{ K_c }[/math] to account for large eddy transport in typical CBL. TKE gives us a measure of the intensity and effectiveness of turbulence and it could be measured accurately.

[math]\displaystyle{ K_c=Sl_ce^{\text{1/2}} }[/math]

where [math]\displaystyle{ S }[/math] is the dimensionless stability function, and [math]\displaystyle{ e }[/math] is the TKE. The diagnostic equations used to obtain parameters [math]\displaystyle{ S }[/math] and [math]\displaystyle{ l_c }[/math] differ in different TKE closures.

4.4. Non-Local Closure

In buoyancy dominated regions, K-theory fails since it always yield unrealistic zero flux in a uniform environment. The non-local characteristics of large buoyancy eddies is accounted for by adding a non-local correction to the local scheme. The flux of any scalar [math]\displaystyle{ c }[/math] can be described with^[9]

[math]\displaystyle{ \overline{w'c'} = - K_c ( \frac{\partial c}{\partial z} - \gamma_c ) }[/math]

Where [math]\displaystyle{ \gamma_c }[/math] is a correction to the local gradient to represent the counter gradient flux transport of large-scale eddies. This term is small in stable conditions, and is therefore, neglected in these conditions. For unstable conditions, however, most transport is done by turbulent eddies with sizes on the order of the depth of the boundary layer.^[9] In such cases,

[math]\displaystyle{ \gamma_c = b \frac{\overline{(w'c')_s}}{w_s} }[/math]

where [math]\displaystyle{ \overline{(w'c')_s} }[/math] is the corresponding surface flux for a scalar [math]\displaystyle{ c }[/math], and [math]\displaystyle{ b }[/math] is a coefficient of proportionality. [math]\displaystyle{ w_s }[/math] is the mixed layer velocity scale defined from surface friction velocity and wind profile function at the surface layer top.

The eddy diffusivity for momentum is defined as

[math]\displaystyle{ K_c=\kappa z w_s (1-\frac{z}{h})^2 }[/math]

where [math]\displaystyle{ \kappa }[/math] is the von Karman constant, [math]\displaystyle{ z }[/math] is the height above the ground, [math]\displaystyle{ h }[/math] is the height of the boundary layer.

Compared to full mixing scheme, the non-local scheme significantly improves simulations of the vertical distributions for NO₂ and O₃, as evaluated in a study done in summer using aircraft measurements. It also reduces model biases at surface over the U.S. by 2-5 ppb for peak O₃ (O₃ concentration is 40-60ppb) in the afternoon, as evaluated using ground observations.^[6]

4.5. Top-Down and Bottom-Up Diffusion

The entrainment fluxes of quantities are not treated in the non-local scheme. In the top-down and bottom-up scheme, both the surface fluxes and the entrainment fluxes are represented. The mean scalar fluxes are the sum of the two fluxes^[10]

[math]\displaystyle{ \overline {w'c'}=\overline{(w'c')_s} (1-z/h_1)+\overline{(w'c')_l} (z/h_1) }[/math]

Where [math]\displaystyle{ h_1 }[/math] is the height of mixed layer. [math]\displaystyle{ \overline{(w'c')_l} }[/math] and [math]\displaystyle{ \overline{(w'c')_s} }[/math] are the scalar flux at the top and bottom of CBL and scale as

File:Model turbulent.tiff

[math]\displaystyle{ \overline{(w'c')_s} =K_s \frac {\partial c_s}{\partial z} }[/math]

[math]\displaystyle{ \overline{(w'c')_l} =K_l \frac {\partial c_l}{\partial z} }[/math]

Where [math]\displaystyle{ K_s }[/math] and [math]\displaystyle{ K_l }[/math] are

[math]\displaystyle{ K_s=\frac {w_*h_1(1-z/h_1)}{g_s} }[/math]

[math]\displaystyle{ K_l=\frac {w_*z}{g_l} }[/math]

[math]\displaystyle{ w_* }[/math] is the convective velocity scale [math]\displaystyle{ w_*=(g \overline{w_s \theta} h_1 T)^\text{1/3} }[/math]. [math]\displaystyle{ g_b }[/math] is the dimensionless gradient for the bottom up direction, a function of [math]\displaystyle{ z/h_1 }[/math]. [math]\displaystyle{ g_l }[/math] is the dimensionless gradient for top-down. The vertical profile of [math]\displaystyle{ g_t }[/math] and [math]\displaystyle{ g_l }[/math] are provided in the Wyngaard et al., 1983 ^[10]