1. Consistency Condition

We may alternatively express the Gent model in the form

$\text{Undefined control sequence cfrac}$

For the model to be consistent with linear elasticity, the following condition has to be satisfied:

$\text{Undefined control sequence cfrac}$

where ${\displaystyle \mu }$ is the shear modulus of the material. Now, at ${\displaystyle I_1=3({\lambda }_i={\lambda }_j=1)}$,

$\text{Undefined control sequence cfrac}$

Therefore, the consistency condition for the Gent model is

$\text{Undefined control sequence cfrac}$

The Gent model assumes that ${\displaystyle J_m\gg 1}$

2. Stress-Deformation Relations

The Cauchy stress for the incompressible Gent model is given by

$\text{Undefined control sequence boldsymbol}$

2.1. Uniaxial Extension

Stress-strain curves under uniaxial extension for Gent model compared with various hyperelastic material models. https://handwiki.org/wiki/index.php?curid=2087400

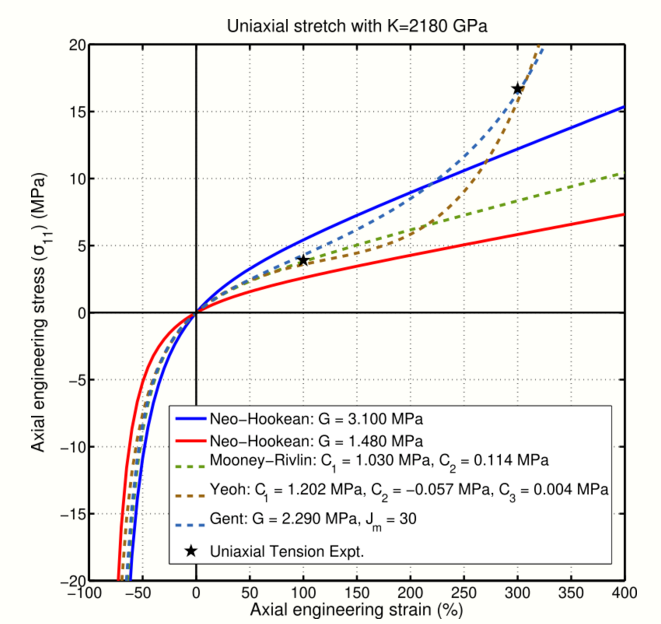
For uniaxial extension in the ${\displaystyle {\mathbf{n}}_1}$-direction, the principal stretches are ${\displaystyle {\lambda }_1=\lambda ,{\lambda }_2={\lambda }_3}$. From incompressibility ${\displaystyle {\lambda }_1{\lambda }_2{\lambda }_3=1}$. Hence ${\displaystyle {\lambda }_2^2={\lambda }_3^2=1/\lambda }$. Therefore,

$\text{Undefined control sequence cfrac}$

The left Cauchy-Green deformation tensor can then be expressed as

$\text{Undefined control sequence boldsymbol}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

$\text{Undefined control sequence cfrac}$

If ${\displaystyle {\sigma }_{22}={\sigma }_{33}=0}$, we have

$\text{Undefined control sequence cfrac}$

Therefore,

$\text{Undefined control sequence cfrac}$

The engineering strain is ${\displaystyle \lambda -1}$. The engineering stress is

$\text{Undefined control sequence cfrac}$

2.2. Equibiaxial Extension

For equibiaxial extension in the ${\displaystyle {\mathbf{n}}_1}$ and ${\displaystyle {\mathbf{n}}_2}$ directions, the principal stretches are ${\displaystyle {\lambda }_1={\lambda }_2=\lambda }$. From incompressibility ${\displaystyle {\lambda }_1{\lambda }_2{\lambda }_3=1}$. Hence ${\displaystyle {\lambda }_3=1/{\lambda }^2}$. Therefore,

$\text{Undefined control sequence cfrac}$

The left Cauchy-Green deformation tensor can then be expressed as

$\text{Undefined control sequence boldsymbol}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

$\text{Undefined control sequence cfrac}$

The engineering strain is ${\displaystyle \lambda -1}$. The engineering stress is

$\text{Undefined control sequence cfrac}$

2.3. Planar Extension

Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the ${\displaystyle {\mathbf{n}}_1}$ directions with the ${\displaystyle {\mathbf{n}}_3}$ direction constrained, the principal stretches are ${\displaystyle {\lambda }_1=\lambda ,{\lambda }_3=1}$. From incompressibility ${\displaystyle {\lambda }_1{\lambda }_2{\lambda }_3=1}$. Hence ${\displaystyle {\lambda }_2=1/\lambda }$. Therefore,

$\text{Undefined control sequence cfrac}$

The left Cauchy-Green deformation tensor can then be expressed as

$\text{Undefined control sequence boldsymbol}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

$\text{Undefined control sequence cfrac}$

The engineering strain is ${\displaystyle \lambda -1}$. The engineering stress is

$\text{Undefined control sequence cfrac}$

2.4. Simple Shear

The deformation gradient for a simple shear deformation has the form^[1]

$\text{Undefined control sequence boldsymbol}$

where ${\displaystyle {\mathbf{e}}_1,{\mathbf{e}}_2}$ are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by

$\text{Undefined control sequence cfrac}$

In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as

$\text{Undefined control sequence boldsymbol}$

Therefore,

$\text{Undefined control sequence boldsymbol}$

and the Cauchy stress is given by

$\text{Undefined control sequence boldsymbol}$

In matrix form,

$\text{Undefined control sequence boldsymbol}$