
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Vivi Li | -- | 1302 | 2022-11-21 01:42:38 |
Video Upload Options
Yuktibhāṣā (Malayalam: യുക്തിഭാഷ, lit. 'Rationale'), also known as Gaṇita-yukti-bhāṣā:xxi and Gaṇitanyāyasaṅgraha (Compendium of Astronomical Rationale), is a major treatise on mathematics and astronomy, written by the India n astronomer Jyesthadeva of the Kerala school of mathematics around 1530. The treatise, written in Malayalam, is a consolidation of the discoveries by Madhava of Sangamagrama, Nilakantha Somayaji, Parameshvara, Jyeshtadeva, Achyuta Pisharati, and other astronomer-mathematicians of the Kerala school. It also exists in a Sanskrit version, with unclear author and date, composed as a rough translation of the Malayalam original. The work contains proofs and derivations of the theorems that it presents. Modern historians used to assert, based on the works of Indian mathematics that first became available, that early Indian scholars in astronomy and computation lacked in proofs, but Yuktibhāṣā demonstrates otherwise. Some of its important topics include the infinite series expansions of functions; power series, including of π and π/4; trigonometric series of sine, cosine, and arctangent; Taylor series, including second and third order approximations of sine and cosine; radii, diameters and circumferences; and tests of convergence. Yuktibhāṣā mainly gives rationale for the results in Nilakantha's Tantra Samgraha. It is considered an early text on the ideas of calculus, predating Newton and Leibniz by centuries. The treatise was largely unnoticed outside India, as it was written in the local language of Malayalam. In modern times, due to wider international cooperation in mathematics, the wider world has taken notice of the work. For example, both Oxford University and the Royal Society of Great Britain have given attribution to pioneering mathematical theorems of Indian origin that predate their Western counterparts.
1. Contents
Yuktibhāṣā contains most of the developments of the earlier Kerala school, particularly Madhava and Nilakantha. The text is divided into two parts – the former deals with mathematical analysis and the latter with astronomy.[1] Beyond this, the continuous text does not have any further division into subjects or topics, so published editions divide the work into chapters based on editorial judgment.[2]:xxxvii
1.1. Mathematics
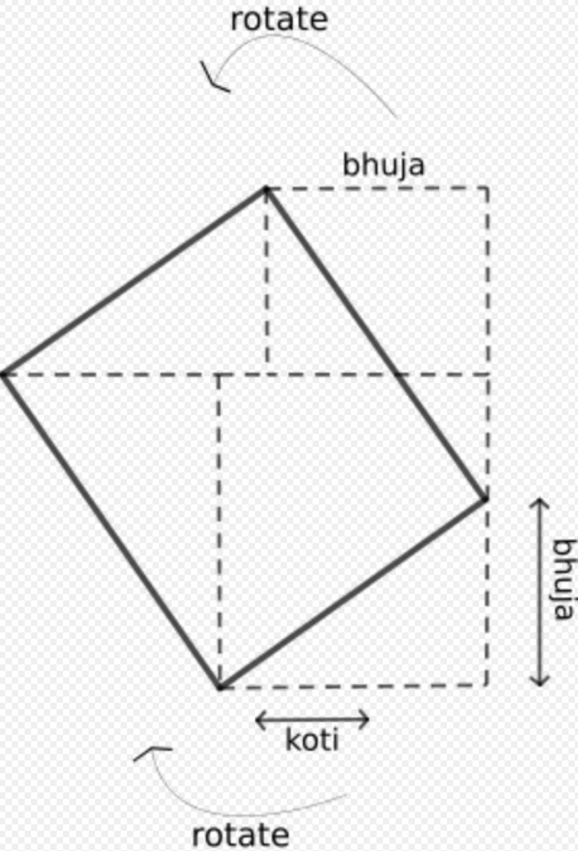
This subjects treated in the mathematics part of the Yuktibhāṣā can be divided into seven chapters:[2]:xxxvii
- parikarma: logistics (the eight mathematical operations)
- daśapraśna: ten problems involving logistics
- bhinnagaṇita: arithmetic of fractions
- trairāśika: rule of three
- kuṭṭakāra: pulverisation (linear indeterminate equations)
- paridhi-vyāsa: relation between circumference and diameter: infinite series and approximations for the ratio of the circumference and diameter of a circle
- jyānayana: derivation of Rsines: infinite series and approximations for sines.[3]
The first four chapters of the contain elementary mathematics, such as division, the Pythagorean theorem, square roots, etc.[4] Novel ideas are not discussed until the sixth chapter on circumference of a circle. Yuktibhāṣā contains a derivation and proof for the power series of inverse tangent, discovered by Madhava.[5] In the text, Jyesthadeva describes Madhava's series in the following manner:
| “ | The first term is the product of the given sine and radius of the desired arc divided by the cosine of the arc. The succeeding terms are obtained by a process of iteration when the first term is repeatedly multiplied by the square of the sine and divided by the square of the cosine. All the terms are then divided by the odd numbers 1, 3, 5, .... The arc is obtained by adding and subtracting respectively the terms of odd rank and those of even rank. It is laid down that the sine of the arc or that of its complement whichever is the smaller should be taken here as the given sine. Otherwise the terms obtained by this above iteration will not tend to the vanishing magnitude. | ” |
In modern mathematical notation,
- [math]\displaystyle{ r\theta={r\frac{\sin\theta}{\cos\theta}} -\frac{r}{3}\frac{\sin^3\theta}{\cos^3\theta} +\frac{r}{5}\frac{\sin^5\theta}{\cos^5\theta} -\frac{r}{7}\frac{\sin^7\theta}{\cos^7\theta} +\cdots }[/math]
or, expressed in terms of tangents,
- [math]\displaystyle{ \theta = \tan\theta - \frac13 \tan^3\theta + \frac15 \tan^5\theta - \cdots \ , }[/math]
which has been previously attributed to James Gregory, who published it in 1667.
The text also contains Madhava's infinite series expansion of π which he obtained from the expansion of the arc-tangent function.
- [math]\displaystyle{ \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots + \frac{(-1)^n}{2n + 1} + \cdots }[/math]
Using a rational approximation of this series, he gave values of the number π as 3.14159265359, correct to 11 decimals, and as 3.1415926535898, correct to 13 decimals.
The text describes two methods for computing the value of π. First, obtain a rapidly converging series by transforming the original infinite series of π. By doing so, the first 21 terms of the infinite series
- [math]\displaystyle{ \pi = \sqrt{12}\left(1-{1\over 3\cdot3}+{1\over5\cdot 3^2}-{1\over7\cdot 3^3}+\cdots\right) }[/math]
was used to compute the approximation to 11 decimal places. The other method was to add a remainder term to the original series of π. The remainder term[math]\displaystyle{ \frac{n^2 + 1}{4n^3 + 5n} }[/math] was used in the infinite series expansion of [math]\displaystyle{ \frac{\pi}{4} }[/math] to improve the approximation of π to 13 decimal places of accuracy when n=76.
Apart from these, the Yuktibhāṣā contains many elementary and complex mathematical topics, including,
- Proofs for the expansion of the sine and cosine functions
- The sum and difference formulae for sine and cosine
- Integer solutions of systems of linear equations (solved using a system known as kuttakaram)
- Geometric derivations of series
- Early statements of Taylor series for some functions
- Tests of convergence for sums .
- .[6]
1.2. Astronomy
Chapters eight to seventeen deal with subjects of astronomy: planetary orbits, celestial spheres, ascension, declination, directions and shadows, spherical triangles, ellipses, and parallax correction. The planetary theory described in the book is similar to that later adopted by Danish astronomer Tycho Brahe.[7] The topics covered in the eight chapters are computation of mean and true longitudes of planets, Earth and celestial spheres, fifteen problems relating to ascension, declination, longitude, etc., determination of time, place, direction, etc., from gnomonic shadow, eclipses, Vyatipata (when the sun and moon have the same declination), visibility correction for planets and phases of the moon.[3]
Specifically,[2]:xxxviii
- grahagati: planetary motion, bhagola: sphere of the zodiac, madhyagraha: mean planets, sūryasphuṭa: true sun, grahasphuṭa: true planets
- bhū-vāyu-bhagola: spheres of the earth, atmosphere, and asterisms, ayanacalana: precession of the equinoxes
- pañcadaśa-praśna: fifteen problems relating to spherical triangles
- dig-jñāna: orientation, chāyā-gaṇita: shadow computations, lagna: rising point of the ecliptic, nati-lambana: parallaxes of latitude and longitude
- grahaṇa: eclipse
- vyatīpāta
- visibility correction of planets
- moon's cusps and phases of the moon
2. Modern Editions
The importance of Yuktibhāṣā was brought to the attention of modern scholarship by C. M. Whish in 1832 through a paper published in the Transactions of the Royal Asiatic Society of Great Britain and Ireland.[8] The mathematics part of the text, along with notes in Malayalam, was first published in 1948 by Rama Varma Thampuran and Akhileswara Aiyar.[1][9]
The first critical edition of the entire Malayalam text, alongside an English translation and detailed explanatory notes, was published in two volumes by Springer[10] in 2008.[2] A third volume, containing a critical edition of the Sanskrit Ganitayuktibhasa, was published by the Indian Institute of Advanced Study, Shimla in 2009.[11][12][13][14]
This edition of Yuktibhasa has been divided into two volumes: Volume I deals with mathematics and Volume II treats astronomy. Each volume is divided into three parts: First part is an English translation of the relevant Malayalam part of Yuktibhasa, second part contains detailed explanatory notes on the translation, and in the third part the text in the Malayalam original is reproduced. The English translation is by K.V. Sarma and the explanatory notes are provided by K. Ramasubramanian, M. D. Srinivas, and M. S. Sriram.[2]
An open access edition of Yuktibhasa is published by Sayahna Foundation in 2020.[15]
References
- K V Sarma; S Hariharan (1991). "Yuktibhāṣā of Jyeṣṭhadeva: A book on rationales in Indian Mathematics and Astronomy: An analytic appraisal". Indian Journal of History of Science 26 (2). http://www.new.dli.ernet.in/insa/INSA_1/20005ac0_185.pdf. Retrieved 9 July 2006.
- Sarma, K.V.; Ramasubramanian, K.; Srinivas, M.D.; Sriram, M.S. (2008). Ganita-Yukti-Bhasa (Rationales in Mathematical Astronomy) of Jyesthadeva. Sources and Studies in the History of Mathematics and Physical Sciences. I-II (1st ed.). Springer (jointly with Hindustan Book Agency, New Delhi). pp. LXVIII, 1084. ISBN 978-1-84882-072-2. Bibcode: 2008rma..book.....S. https://www.springer.com/math/history+of+mathematics/book/978-1-84882-072-2. Retrieved 17 December 2009.
- For more details on contents see Kinokuniya DataBase: "Ganita-yukti-bhasa (Rationales in Mathematical Astronomy) of Jyesthadeva". http://bookwebpro.kinokuniya.co.jp/booksea.cgi?ISBN=1848820720http://www.buscalibros.cl/libro.php?libro=2104208.
- "The Yuktibhasa Calculus Text". The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala. Dr Sarada Rajeev. http://www.canisius.edu/topos/archives/rajeev2.pdf.
- "The Kerala School, European Mathematics and Navigation". Indian Mathemematics. D.P. Agrawal – Infinity Foundation. http://www.infinityfoundation.com/mandala/t_es/t_es_agraw_kerala.htm.
- "Science and technology in free India". Government of Kerala – Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. http://www.kerala.gov.in/keralcallsep04/p22-24.pdf.
- "Science and Mathematics in India". South Asian History. India Resources. http://india_resource.tripod.com/mathematics.htm.
- Divakaran, P. P. (2007). "The First Textbook of Calculus: "Yuktibhāṣā"". Journal of Indian Philosophy 35 (5/6): 417–443. doi:10.1007/s10781-007-9029-1. ISSN 0022-1791. https://dx.doi.org/10.1007%2Fs10781-007-9029-1
- Yuktibhâsâ, Part I (ed) with notes by Ramavarma (Maru) Thampuran and A. R. Akhileswara Aiyer, Magalodayam Ltd., Trichur, Kerala, 1123 Malayalam Era, 1948 CE.
- See publishers's (Springer's) web page on the book: Ganita-Yukti-Bhasa (Rationales in Mathematical Astronomy) of Jyesthadeva. ISBN 9781848820722. https://www.springer.com/mathematics/history+of+mathematics/book/978-1-84882-072-2. Retrieved 29 April 2010.
- Sarma, K.V. (2009) (in ml, en). Ganita Yuktibhasa. III. Indian Institute of Advanced Study, Shimla, India. ISBN 978-81-7986-052-6. http://www.iias.org/p_ganita_yuktibhasa_volume-III.html. Retrieved 16 December 2009.
- K.V. Sarma (2004). Ganita Yuktibhasa (Volume III). Shimla: Indian Institute of Advanced Study. ISBN 81-7986-052-3.
- Publisher's (Indian Institute of Advanced Study) web page on the book:"Ganita Yuktibhasa by K.V. Sarma". http://www.iias.org/p_ganita_yuktibhasa_volume-III.html.
- For a review of Ganita-yukti-bhasa (Rationales in Mathematical Astronomy) of Jyesthadeva by Mathematical Association of America see : Homer S. White (2009-07-17). "Ganita-Yukti-Bhāsā (Rationales in Mathematical Astronomy) of Jyesthadeva". The Mathematical Association of America. https://www.maa.org/press/maa-reviews/ganita-yukti-bh-s-rationales-in-mathematical-astronomy-of-jyesthadeva.
- Sayahna Foundation (2020-11-20). "Yukthibhasha digital edition". https://books.sayahna.org/ml/pdf/yukthibhasha.pdf.




