1. Physical Process

At sufficiently low temperatures and high magnetic fields, the free electrons in the conduction band of a metal, semimetal, or narrow band gap semiconductor will behave like simple harmonic oscillators. When the magnetic field strength is changed, the oscillation period of the simple harmonic oscillators changes proportionally. The resulting energy spectrum is made up of Landau levels separated by the cyclotron energy. These Landau levels are further split by the Zeeman energy. In each Landau level the cyclotron and Zeeman energies and the number of electron states (eB/h) all increase linearly with increasing magnetic field. Thus, as the magnetic field increases, the spin-split Landau levels move to higher energy. As each energy level passes through the Fermi energy, it depopulates as the electrons become free to flow as current. This causes the material's transport and thermodynamic properties to oscillate periodically, producing a measurable oscillation in the material's conductivity. Since the transition across the Fermi 'edge' spans a small range of energies, the waveform is square rather than sinusoidal, with the shape becoming ever more square as the temperature is lowered .

2. Theory

Consider a two-dimensional quantum gas of electrons confined in a sample with given width and with edges. In the presence of a magnetic flux density B, the energy eigenvalues of this system are described by Landau levels. As shown in Fig 1, these levels are equidistant along the vertical axis. Each energy level is substantially flat inside a sample (see Fig 1). At the edges of a sample, the work function bends levels upwards.

Fig 1: Edge channels of a sample with a two-dimensional electron gas. https://handwiki.org/wiki/index.php?curid=2056058

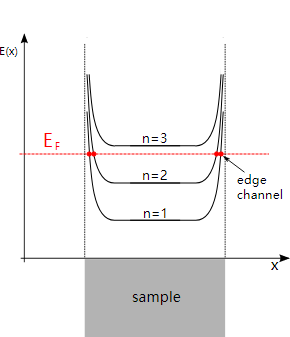
Fig 1 shows the Fermi energy E_F located in between^[1] two Landau levels. Electrons become mobile as their energy levels cross the Fermi energy E_F. With the Fermi energy E_F in between two Landau levels, scattering of electrons will occur only at the edges of a sample where the levels are bent. The corresponding electron states are commonly referred to as edge channels.

The Landauer-Büttiker approach is used to describe transport of electrons in this particular sample. The Landauer-Büttiker approach allows calculation of net currents I_m flowing between a number of contacts 1 ≤ m ≤ n. In its simplified form, the net current I_m of contact m with chemical potential µ_m reads

[math]\displaystyle{ I_m = 2 \frac{e\cdot i}{h} \left(\mu_m - \sum_{l\neq m} T_{ml} \mu_l \right),\, }[/math]

where e denotes the electron charge, h denotes Planck's constant, and i stands for the number of edge channels.^[2] The matrix T_ml denotes the probability of transmission of a negatively charged particle (i.e. of an electron) from a contact l ≠ m to another contact m. The net current I_m in relationship (1) is made up of the currents towards contact m and of the current transmitted from the contact m to all other contacts l ≠ m . That current equals the voltage μ_m / e of contact m multiplied with the Hall conductivity of 2 e² / h per edge channel.

Fig 2: Contact arrangement for measurement of SdH oscillations. https://handwiki.org/wiki/index.php?curid=1715774

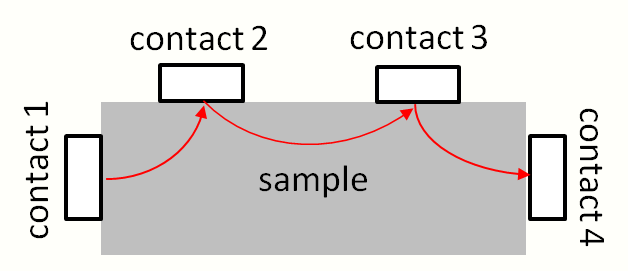
Fig 2 shows a sample with four contacts. To drive a current through the sample, a voltage is applied between the contacts 1 and 4. A voltage is measured between the contacts 2 and 3. Suppose electrons leave the 1st contact, then are transmitted from contact 1 to contact 2, then from contact 2 to contact 3, then from contact 3 to contact 4, and finally from contact 4 back to contact 1. A negative charge (i.e. an electron) transmitted from contact 1 to contact 2 will result in a current from contact 2 to contact 1. An electron transmitted from contact 2 to contact 3 will result in a current from contact 3 to contact 2 etc. Suppose also that no electrons are transmitted along any further paths. The probabilities of transmission of ideal contacts then read

[math]\displaystyle{ T_{21} = T_{32} = T_{43} = T_{14} = 1, }[/math]

and

[math]\displaystyle{ T_{ml} = 0 }[/math]

otherwise. With these probabilities, the currents I₁ ... I₄ through the four contacts, and with their chemical potentials µ₁ ... µ₄, equation (1) can be re-written

[math]\displaystyle{ \left(\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix}\right)=\frac{2e\cdot i}{h}\left(\begin{matrix} 1 & 0 & 0 & -1 \\ -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \end{matrix}\right)\left(\begin{matrix} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{matrix}\right). }[/math]

A voltage is measured between contacts 2 and 3. The voltage measurement should ideally not involve a flow of current through the meter, so I₂ = I₃ = 0. It follows that

[math]\displaystyle{ I_3 = 0 = \frac{2e\cdot i}{h} \left(-\mu_2 + \mu_3\right), }[/math]

[math]\displaystyle{ \mu_2 = \mu_3. }[/math]

In other words, the chemical potentials µ₂ and µ₃ and their respective voltages µ₂/e and µ₃/e are the same. As a consequence of no drop of voltage between the contacts 2 and 3, the current I₁ experiences zero resistivity R_SdH in between contacts 2 and 3

[math]\displaystyle{ R_{\mathrm{SdH}} = \frac{\mu_2 - \mu_3}{e\cdot I_1}=0. }[/math]

The result of zero resistivity between the contacts 2 and 3 is a consequence of the electrons being mobile only in the edge channels of the sample. The situation would be different if a Landau level came close to the Fermi energy E_F. Any electrons in that level would become mobile as their energy approaches the Fermi energy E_F. Consequently, scatter would lead to R_SdH > 0. In other words, the above approach yields zero resistivity whenever the Landau levels are positioned such that the Fermi energy E_F is in between two levels.

3. Applications

Shubnikov–De Haas oscillations can be used to determine the two-dimensional electron density of a sample. For a given magnetic flux [math]\displaystyle{ \Phi }[/math] the maximum number D of electrons with spin S = 1/2 per Landau level is

[math]\displaystyle{ D = \left(2 S + 1\right) \frac{\Phi}{\Phi_0} = 2 \frac{\Phi}{\Phi_0}.\, }[/math]

Upon insertion of the expressions for the flux quantum Φ₀ = h / e and for the magnetic flux Φ = B ∙ A relationship (2) reads

[math]\displaystyle{ D = 2 \frac{e\cdot B\cdot A}{h} }[/math]

Let N denote the maximum number of states per unit area, so D = N ∙ A and

[math]\displaystyle{ N = 2 \frac{e\cdot B}{h}. }[/math]

Now let each Landau level correspond to an edge channel of the above sample. For a given number i of edge channels each filled with N electrons per unit area, the overall number n of electrons per unit area will read

[math]\displaystyle{ n = i\cdot N = 2 \cdot i \cdot \frac{e\cdot B}{h}. }[/math]

The overall number n of electrons per unit area is commonly referred to as the electron density of a sample. No electrons disappear from the sample into the unknown, so the electron density n is constant. It follows that

[math]\displaystyle{ B_i = \frac{n\cdot h}{2 \cdot e \cdot i}, }[/math]

[math]\displaystyle{ \frac{1}{B_i} = \frac{2 \cdot e \cdot i}{n\cdot h}, }[/math]

[math]\displaystyle{ \Delta\left(\frac{1}{B}\right) = \frac{1}{B_{i+1}}-\frac{1}{B_i} = \frac{2 \cdot e}{n\cdot h}.\, }[/math]

Fig 3: Inverse magnetic flux densities 1/B_i vs Shubnikov–De Haas minima as observed in highly doped Bi₂Se₃. https://handwiki.org/wiki/index.php?curid=1614972

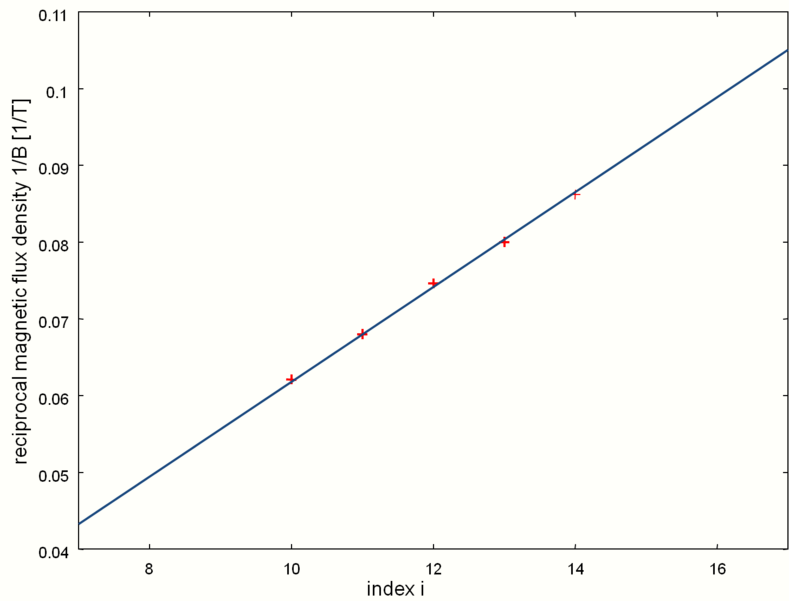
For a given sample, all factors including the electron density n on the right hand side of relationship (3) are constant. When plotting the index i of an edge channel versus the reciprocal of its magnetic flux density 1/B_i, one obtains a straight line with slope 2 ∙ e/(n∙ h). Since the electron charge e is known and also Planck's constant h, one can derive the electron density n of a sample from this plot.^[3] Shubnikov–De Haas oscillations are observed in highly doped Bi₂Se₃.^[4] Fig 3 shows the reciprocal magnetic flux density 1/B_i of the 10th to 14th minima of a Bi₂Se₃ sample. The slope of 0.00618/T as obtained from a linear fit yields the electron density n

[math]\displaystyle{ n = \frac{2\cdot e}{0.00618/\mathrm{T}\cdot h} \approx 7.82 \cdot 10^{14}/\mathrm{m}^2. }[/math]

Shubnikov–De Haas oscillations can be used to map the Fermi surface of electrons in a sample, by determining the periods of oscillation for various applied field directions.

4. Related Physical Process

The effect is related to the De Haas–Van Alphen effect, which is the name given to the corresponding oscillations in magnetization. The signature of each effect is a periodic waveform when plotted as a function of inverse magnetic field. The "frequency" of the magnetoresistance oscillations indicate areas of extremal orbits around the Fermi surface. The area of the Fermi surface is expressed in teslas.