Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yunpeng Xue
 -- 1512 2022-11-16 01:26:54 |
2 format corrected.
Beatrix Zheng
 Meta information modification 1512 2022-11-16 10:58:51 | |
3 figures without permission are removed.
Yunpeng Xue
 -39 word(s) 1473 2022-11-16 11:08:32 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Xue, Y.;  Stewart, C.;  Kelly, D.;  Campbell, D.;  Gormley, M. The Wavy Liquid Film. Encyclopedia. Available online: https://encyclopedia.pub/entry/34731 (accessed on 29 April 2024).
Xue Y,  Stewart C,  Kelly D,  Campbell D,  Gormley M. The Wavy Liquid Film. Encyclopedia. Available at: https://encyclopedia.pub/entry/34731. Accessed April 29, 2024.
Xue, Yunpeng, Colin Stewart, David Kelly, David Campbell, Michael Gormley. "The Wavy Liquid Film" Encyclopedia, https://encyclopedia.pub/entry/34731 (accessed April 29, 2024).
Xue, Y.,  Stewart, C.,  Kelly, D.,  Campbell, D., & Gormley, M. (2022, November 16). The Wavy Liquid Film. In Encyclopedia. https://encyclopedia.pub/entry/34731
Xue, Yunpeng, et al. "The Wavy Liquid Film." Encyclopedia. Web. 16 November, 2022.
The Wavy Liquid Film
Edit
This entry is adapted from the peer-reviewed paper 10.3390/w14213496

Two-phase annular flow in vertical pipes is one of the most common and important flow regimes in fluid mechanics, particularly in the field of building drainage systems where discharges to the vertical pipe are random and the flow is unsteady. With the development of experimental techniques and analytical methods, the understanding of the fundamental mechanism of the annular two-phase flow has been significantly advanced, such as liquid film development, evolution of the disturbance wave, and droplet entrainment mechanism. 

two-phase flow annular flow experimental techniques

1. Fundamental Understanding of the Liquid Film

For an annular two-phase flow in a vertical pipe, the peripheral liquid film generally includes ripple and disturbance waves and acts as a thin wall for the gaseous core flow with entrained drops, as shown in Figure 1. Annular flow gets stable when the fluid has higher effective viscosity (molecular and turbulent viscosity) in the core region and lower viscosity fluid in the annulus [1]. Several definitions are frequently used in the field to describe the flow, such as instantaneous film thickness, the average thickness of base film/substrate, average film thickness, and local maximum thickness. The liquid film thickness is determined by the piping system configuration and the flow conditions such as the liquid flow rate, fluid (gas/liquid) properties, and flow directions. The average liquid film thickness has been well documented in previous research and new understandings of the mechanism have been reported in the recent two decades due to the advanced experimental methods and techniques.
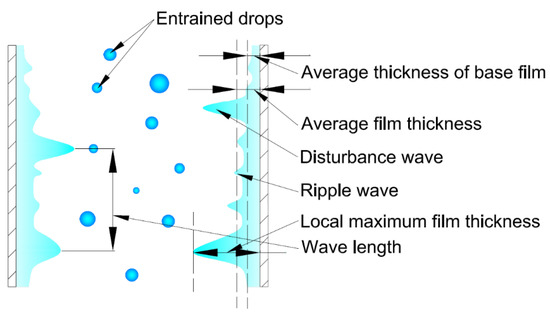
Water 14 03496 g011 550
Figure 1. Structure of a typical two-phase annular flow in vertical pipe showing the disturbance waves, ripple waves, liquid film, and entrained droplets.
Film thickness distribution captured directly from LIF results [2][3][4][5] (Figure 2) is found similar across a wide range of flow conditions, although the absolute film thickness changes significantly. The average film thickness and the fluctuation of film thickness decreased with gas flow velocity and increased with the liquid flow velocity and the relationship between the average film thickness and the roughness is determined by the liquid and gas flows [6]. Zhao et al. [7] collected high-frequency film thickness data of a gas-liquid annular flow and found the film variation along the axial direction was not significant (within ±10% of average values). The development of the average thickness was only near the inlet, i.e., up to L/D=20 (ReL = 211) and L/D=25 (ReL = 603). Prior to becoming fully developed, the film decelerates first to a local maximum thickness and then accelerates again to become thinner.
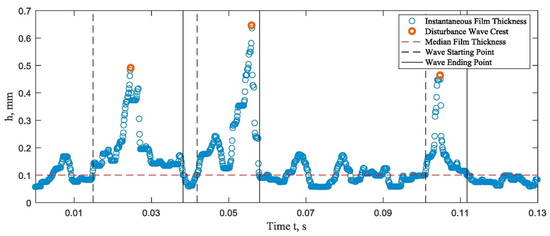
Water 14 03496 g012 550
Figure 2. Film thickness distribution conducted from BBLIF [4].
It is well understood that the film thickness generally decreases with the decrease in the liquid superficial velocity and increases in the gas superficial velocity [8][9][10][11][12][13][14][15][16][17]. The liquid film was reported to have 3-D structures with a large height fluctuation in circumferential and axial directions, and a meandering path between the maximum height around the circumference [18][19]. This fluctuation is mainly caused by the non-uniform generation of the ripple wave and disturbance waves. This difference in film thickness in circumferential directions was also observed from LIF results [20][21] conductive probe measurements [7][22]. It was found that the average length of the disturbance waves was similar to the pipe diameter and independent of the gas/liquid superficial velocities [22].
A good agreement between the Nusselt’s predictions and experimental velocity profiles was found at low liquid Reynolds number and significant differences between the measured and Nusselt’s predicted profiles were reported in wavy turbulent films, i.e., high Reynolds number [23]. The measured average film thickness data (PLIF) agreed well with previous experimental data and was compared with Nusselt’s theory [10]. The visualization results also proved the existence of recirculation zones in front of disturbance waves [24]. Like the velocity profiles within the wavy film, the film thickness was well-described by the Nusselt flow predictions at low ReL, while with increasing ReL, the film thickness was increasingly underpredicted by the theory, but with good agreement with Mudawwar and El-Masri’s semi-empirical turbulence model [25].
Vassallo [26] conducted a near-wall measurement of velocity in the liquid film using a hot-film probe. A modified law of the wall was suggested for annular two-phase flows near the transition regime when the film was thicker. Muñoz-Cobo et al. [27] focused on the effect of the liquid surface tension in vertical annular flow by having different amounts of 1-butanol in the fluid. Reducing the surface tension leads to a reduction in the intermolecular cohesion forces, easier entrainment of the small droplets from the wave peaks and a decrease in the wave amplitude.

2. Disturbance Wave Characteristics

Based on the experimental and numerical results, Fan et al. [28] reported the main progress of wave evolution, i.e., generation and development of initial waves, coalescence of initial disturbance waves into large-scale waves, and acceleration of waves with further stable propagation. They also found that the waves generated slow and fast ripples on their rear slopes and droplet entrainment started from the disruption of fast ripples. The disturbance waves were observed only when the liquid film Reynolds numbers exceeded the critical value [7]. Dao and Balakotaiah [29] investigated the occlusion of falling film in a vertical pipe with glycerine. The experimental results reported a good correlation between the liquid Reynolds number, the Kapitza number, and the Bond number. Han et al. [30] studied the effects of gas flow on the disturbance wave in the annular flow. With a constant liquid flow rate, an increase in the gas mass flow rate resulted in a series of changes in the wave characteristics, i.e., decreased wave spacing and increased wave frequency, slightly decreases in wave base height, peak height, and the mean film thickness. They also reported a much more significant increase in the liquid velocity from the base area to the wavy area with an approximate ratio of 1:14.
Alekseenko et al. [20][21][31][32] reported quantitative studies of the disturbance wave focusing on its spatial and temporal evolution. Three different regions were defined in the liquid film: the crests of disturbance waves, where the fast ripples existed; the back slopes of disturbance waves, where the slow ripples were generated and their properties gradually changed with increasing distance from the crests; and the base film, where the properties of slow ripples had stabilized values. Rapid changes in the film flow parameters, including the thickness, disturbance wave velocity, and frequency, were found within the first 50 tube diameters [13]. The disturbance waves were found to appear and to achieve the stable circumferential distribution at 5–10 pipe diameters from the injection and this coherence gradually strengthened downstream [7].
The identification of the flow pattern and the pressure gradient was determined by the characteristics and behaviours of the interfacial wave [33][34], and its orientation has significant impacts on the flow identification and pressure gradient. Pressure drop in a downward co-current annular flow measured by Hajiloo et al. [35] suggested that at a fixed gas Reynolds number, a large increase in interfacial friction accompanied a decrease in tube diameter and existing correlations were unsuccessful for the present data.

3. Correlations of the Film Thickness

Klyuev and Solov’eva [36] developed a mathematical model for the annular flow, which showed the increase in void fraction resulted in decreases in the average film thickness and the average liquid velocity. Belt et al. [17] improved the Wallis correlation by correcting the film roughness, which was assumed as four times the mean film thickness. The new sand-grain roughness was found proportional to the wave height and can be estimated using the roughness density. The transient behaviour model [37] and critical friction factor model [38][39] were developed to estimate the averaged film thicknesses. The calculated results were agreed to within 20% of the experimental measurements. The liquid film at the top was found significantly different from those at the lower axial positions [16], which had a distinctly different slope from the published correlations and theoretical predictions, and hence suggested a potential change in the film structure in large-scale pipes.

4. The Void Fraction of Annular Two-Phase Flow

The void fraction is the fraction of the gaseous phase to the total volume of the channel, which is generally between 0.65 and 0.98. Godbole et al. [40] conducted a comprehensive literature review of the void fraction correlations and experimental results in the early years of upward two-phase flow. Most area-averaged void fraction had an increasing trend along the axial direction and decreased after a maximum value of around 80–100 diameters downstream [16][41][42]. However, the decrease in void fraction in the vertical downward annular flow was also observed in some conditions which was a result of the kinematic shock phenomenon. Alves et al. [37] developed a three-field two-phase flow model to simulate the transient annular flow in vertical pipes with a slight tendency of underprediction. Smith et al. [43] proposed a one-dimensional interfacial area transport equation (IATE) using measurements of local void fraction, interfacial area concentration, and interface velocity of an upward annular flow in a large pipe. The dependence of mixture density on the void fraction and correlations based on the slip ratio and drift flux model were analysed [44].

References

  1. Joseph, D.D.; Bannwart, A.C.; Liu, Y.J. Stability of annular flow and slugging. Int. J. Multiph. Flow 1996, 22, 1247–1254.
  2. van Eckeveld, A.C.; Gotfredsen, E.; Westerweel, J.; Poelma, C. Annular two-phase flow in vertical smooth and corrugated pipes. Int. J. Multiph. Flow 2018, 109, 150–163.
  3. Schubring, D.; Ashwood, A.C.; Shedd, T.A.; Hurlburt, E.T. Planar laser-induced fluorescence (PLIF) measurements of liquid film thickness in annular flow. Part I: Methods and data. Int. J. Multiph. Flow 2010, 36, 815–824.
  4. Vasques, J.; Cherdantsev, A.; Cherdantsev, M.; Isaenkov, S.; Hann, D. Comparison of disturbance wave parameters with flow orientation in vertical annular gas-liquid flows in a small pipe. Exp. Therm. Fluid Sci. 2018, 97, 484–501.
  5. Charogiannis, A.; An, J.S.; Voulgaropoulos, V.; Markides, C.N. Structured planar laser-induced fluorescence (S-PLIF) for the accurate identification of interfaces in multiphase flows. Int. J. Multiph. Flow 2019, 118, 193–204.
  6. Schubring, D.; Shedd, T.A.; Hurlburt, E.T. Planar laser-induced fluorescence (PLIF) measurements of liquid film thickness in annular flow. Part II: Analysis and comparison to models. Int. J. Multiph. Flow 2010, 36, 825–835.
  7. Zhao, Y.; Markides, C.N.; Matar, O.K.; Hewitt, G.F. Disturbance wave development in two-phase gas-liquid upwards vertical annular flow. Int. J. Multiph. Flow 2013, 55, 111–129.
  8. Van der Meulen, G.P. Churn-Annular Gas-Liquid Flows in Large Diameter Vertical Pipes. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2012.
  9. Pan, L.M.; He, H.; Ju, P.; Hibiki, T.; Ishii, M. Experimental study and modeling of disturbance wave height of vertical annular flow. Int. J. Heat Mass Transf. 2015, 89, 165–175.
  10. Zadrazil, I.; Matar, O.K.; Markides, C.N. An experimental characterization of downwards gas-liquid annular flow by laser-induced fluorescence: Flow regimes and film statistics. Int. J. Multiph. Flow 2014, 60, 87–102.
  11. Alamu, M.B.; Azzopardi, B.J. Simultaneous investigation of entrained liquid fraction, liquid film thickness and pressure drop in vertical annular flow. J. Energy Resour. Technol. Trans. ASME 2011, 133, 023103.
  12. Al-Yarubi, Q. Phase Flow Rate Measurements of Annular Flows. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2010.
  13. Wolf, A.; Jayanti, S.; Hewitt, G.F. Flow development in vertical annular flow. Chem. Eng. Sci. 2001, 56, 3221–3235.
  14. Sawant, P.; Ishii, M.; Hazuku, T.; Takamasa, T.; Mori, M. Properties of disturbance waves in vertical annular two-phase flow. Nucl. Eng. Des. 2008, 238, 3528–3541.
  15. Abdulkadir, M.; Mbalisigwe, U.P.; Zhao, D.; Hernandez-Perez, V.; Azzopardi, B.J.; Tahir, S. Characteristics of churn and annular flows in a large diameter vertical riser. Int. J. Multiph. Flow 2019, 113, 250–263.
  16. Almabrok, A.A.; Aliyu, A.M.; Lao, L.; Yeung, H. Gas/liquid flow behaviours in a downward section of large diameter vertical serpentine pipes. Int. J. Multiph. Flow 2016, 78, 25–43.
  17. Belt, R.J.; Van’t Westende, J.M.C.; Portela, L.M. Prediction of the interfacial shear-stress in vertical annular flow. Int. J. Multiph. Flow 2009, 35, 689–697.
  18. Xue, T.; Li, Z.; Li, C.; Wu, B. Measurement of thickness of annular liquid films based on distortion correction of laser-induced fluorescence imaging. Rev. Sci. Instrum. 2019, 90, 033103.
  19. Xue, T.; Li, C.; Wu, B. Distortion correction and characteristics measurement of circumferential liquid film based on PLIF. AIChE J. 2019, 65, e16612.
  20. Alekseenko, S.V.; Cherdantsev, A.V.; Heinz, O.M.; Kharlamov, S.M.; Markovich, D.M. Analysis of spatial and temporal evolution of disturbance waves and ripples in annular gas-liquid flow. Int. J. Multiph. Flow 2014, 67, 122–134.
  21. Alekseenko, S.; Cherdantsev, A.; Cherdantsev, M.; Isaenkov, S.; Kharlamov, S.; Markovich, D. Application of a high-speed laser-induced fluorescence technique for studying the three-dimensional structure of annular gas-liquid flow. Exp. Fluids 2012, 53, 77–89.
  22. Belt, R.J.; Westende, J.M.C.V.; Prasser, H.M.; Portela, L.M. Time and spatially resolved measurements of interfacial waves in vertical annular flow. Int. J. Multiph. Flow 2010, 36, 570–587.
  23. Karimi, G.; Kawaji, M. An experimental study of freely falling films in a vertical tube. Chem. Eng. Sci. 1998, 53, 3501–3512.
  24. Zadrazil, I.; Markides, C.N. An experimental characterization of liquid films in downwards co-current gas-liquid annular flow by particle image and tracking velocimetry. Int. J. Multiph. Flow 2014, 67, 42–53.
  25. Mudawwar, I.A.; El-Masri, M.A. Momentum and heat transfer across freely-falling turbulent liquid films. Int. J. Multiph. Flow 1986, 12, 771–790.
  26. Vassallo, P. Near wall structure in vertical air-water annular flows. Int. J. Multiph. Flow 1999, 25, 459–476.
  27. Rivera, Y.; Muñoz-Cobo, J.L.; Cuadros, J.L.; Berna, C.; Escrivá, A. Experimental study of the effects produced by the changes of the liquid and gas superficial velocities and the surface tension on the interfacial waves and the film thickness in annular concurrent upward vertical flows. Exp. Therm. Fluid Sci. 2021, 120, 110224.
  28. Fan, W.; Cherdantsev, A.; Anglart, H. Experimental and numerical study of formation and development of disturbance waves in annular gas-liquid flow. Energy 2020, 207, 118309.
  29. Dao, E.K.; Balakotaiah, V. Experimental study of wave occlusion on falling films in a vertical pipe. AIChE J. 2000, 46, 1300–1306.
  30. Han, H.; Zhu, Z.; Gabriel, K. A study on the effect of gas flow rate on the wave characteristics in two-phase gas–liquid annular flow. Nucl. Eng. Des. 2006, 236, 2580–2588.
  31. Alekseenko, S.V.; Cherdantsev, A.V.; Cherdantsev, M.V.; Isaenkov, S.V.; Markovich, D.M. Study of formation and development of disturbance waves in annular gas-liquid flow. Int. J. Multiph. Flow 2015, 77, 65–75.
  32. Alekseenko, S.; Antipin, V.; Cherdantsev, A.; Kharlamov, S.; Markovich, D. Two-wave structure of liquid film and wave interrelation in annular gas-liquid flow with and without entrainment. Phys. Fluids 2009, 21, 061701.
  33. Lin, R.; Wang, K.; Liu, L.; Zhang, Y.; Dong, S. Study on the characteristics of interfacial waves in annular flow by image analysis. Chem. Eng. Sci. 2020, 212, 115336.
  34. Lin, R.; Wang, K.; Liu, L.; Zhang, Y.; Dong, S. Application of the image analysis on the investigation of disturbance waves in vertical upward annular two-phase flow. Exp. Therm. Fluid Sci. 2020, 114, 110062.
  35. Hajiloo, M.; Chang, B.H.; Mills, A.F. Interfacial shear in downward two-phase annular co-current flow. Int. J. Multiph. Flow 2001, 27, 1095–1108.
  36. Klyuev, N.I.; Solov’eva, E.A. Method for the annular gas-liquid mixture flow regime in a vertical cylindrical channel. Russ. Aeronaut. 2009, 52, 68–71.
  37. Alves, M.V.C.; Waltrich, P.J.; Gessner, T.R.; Falcone, G.; Barbosa, J.R., Jr. Modeling transient churn-annular flows in a long vertical tube. Int. J. Multiph. Flow 2017, 89, 399–412.
  38. Schubring, D.; Shedd, T.A. A model for pressure loss, film thickness, and entrained fraction for gas-liquid annular flow. Int. J. Heat Fluid Flow 2011, 32, 730–739.
  39. Schubring, D.; Shedd, T.A. Critical friction factor modeling of horizontal annular base film thickness. Int. J. Multiph. Flow 2009, 35, 389–397.
  40. Godbole, P.V.; Tang, C.C.; Ghajar, A.J. Comparison of Void Fraction Correlations for Different Flow Patterns in Upward Vertical Two-Phase Flow. Heat Transf. Eng. 2011, 32, 843–860.
  41. Vieira, R.E.; Parsi, M.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A.; Schleicher, E.; Hampel, U. Experimental characterization of vertical gas-liquid pipe flow for annular and liquid loading conditions using dual Wire-Mesh Sensor. Exp. Therm. Fluid Sci. 2015, 64, 81–93.
  42. Vieira, R.E.; Parsi, M.; McLaury, B.S.; Shirazi, S.A.; Torres, C.F.; Schleicher, E.; Hampel, U. Experimental characterization of vertical downward two-phase annular flows using Wire-Mesh Sensor. Chem. Eng. Sci. 2015, 134, 324–339.
  43. Smith, T.R.; Schlegel, J.P.; Hibiki, T.; Ishii, M. Two-phase flow structure in large diameter pipes. Int. J. Heat Fluid Flow 2012, 33, 156–167.
  44. Ghajar, A.J.; Bhagwat, S.M. Effect of void fraction and two-phase dynamic viscosity models on prediction of hydrostatic and frictional pressure drop in vertical upward gas-liquid two-phase flow. Heat Transf. Eng. 2013, 34, 1044–1059.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yunpeng Xue
,
Colin Stewart
,
David Kelly
,
David Campbell
,
Michael Gormley
View Times: 554
Revisions: 3 times (View History)
Update Date: 16 Nov 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback